目前,绝大多数直升机的旋翼都以固定转速工作。这主要是出于对振动、系统复杂程度、发动机及传动技术限制等问题的考虑。但是,固定转速只能使旋翼在给定重量、高度和速度下处于效能最优状态。当重量、高度和速度发生变化时,旋翼的工作状态会偏离其最优位置。现在由于材料技术、发动机技术与传动技术的发展,旋翼变转速技术已经可以实现。通过改变旋翼转速可以使直升机在无地效悬停、最大航时巡航、最大航程巡航和最大速度前飞这4种飞行状态下发挥更好的性能。因为该技术可以尽可能地让更多的桨叶段在最大升/阻比迎角下工作[1],提高直升机的性能和效率。
近年来不断有新的旋翼飞行器通过采用旋翼变转速技术来提高飞行性能,如A160“蜂鸟”长航时无人直升机、X2共轴刚性旋翼高速直升机、V22倾转旋翼机[2]等。同时也有越来越多的研究人员从提高飞行性能的角度展开对旋翼变转速技术的研究。Diottavio与Friedmann[3]对A160的试飞数据进行了分析,得出旋翼变转速技术更适合用于小重量、低海拔的飞行状态。Bowen-Davis和Chopra[4]使用马里兰大学直升机分析软件(University of Maryland advanced rotorcraft code,UMARC)分析了铰接式旋翼在不同转速下总功率、废阻功率、型阻功率、诱导功率、桨盘迎角分布、航程以及航时等的变化。研究表明,适当地降低转速可通过减小型阻功率降低总功率,从而显著地增加航程和航时。韩东[5]探讨了旋翼转速、起飞重量、前飞速度和飞行高度对旋翼性能和配平特性的影响。刘士明等[6]分析了前飞速度、起飞重量和飞行高度如何影响旋翼转速的优化设计,以及厚翼型对最优转速下旋翼性能的影响。可是,改变旋翼转速不仅会带来性能方面的影响,还会在飞行品质、振动、噪声等多个方面引起相应的变化。徐明等[7-10]对变转速旋翼的气动特性与操纵稳定性进行了分析,并且为变转速旋翼直升机的旋翼翼型和总体参数提出了优化设计方法。Datta等[11]通过风洞试验分析UH-60A的旋翼得出了转速降低引起操纵量变化的机理。Berry和Chopra[12]则测量了模型旋翼在不同转速下的振动载荷,测量结果指出在旋翼转速较低时其振动载荷较大。Karem[13]的研究发现通过改变桨叶质量、刚度和弦长的分布可以避免旋翼在转速变化过程中发生共振。上述研究结果表明旋翼转速变化确实会提高直升机的飞行性能,但与此同时还要综合考虑转速变化在其他方面带来的影响。
因此,本文通过旋翼空气动力学、结构动力学、气动声学以及飞行动力学建模,建立适用于变转速旋翼直升机的综合分析模型,用于综合分析直升机稳态飞行时的旋翼需用功率、全机配平操纵、旋翼桨毂振动水平与旋翼气动噪声。并且用UH-60A“黑鹰”直升机的飞行试验数据及相关研究结果对
模型进行验证。以此为基础,进一步综合分析旋翼转速变化对旋翼需用功率、全机配平操纵、旋翼桨毂振动水平与旋翼气动噪声的影响,为变转速旋翼的转速优化设计提供依据。
1 直升机综合建模综合建模的目的是针对变转速旋翼直升机建立性能、操纵、振动及噪声的理论模型。为确定稳定飞行状态下直升机的旋翼需用功率、全机配平操纵、旋翼桨毂振动水平和旋翼气动噪声提供分析方法。
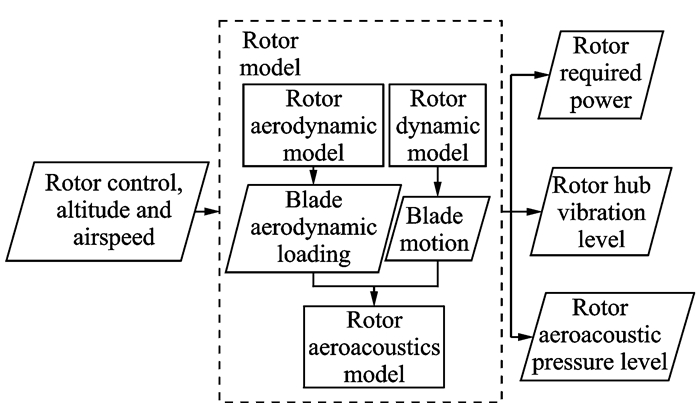
1.1 旋翼模型为了满足综合分析的需要,旋翼模型从旋翼的操纵量、姿态与运动速度出发,通过翼型气动模型、旋翼入流模型、旋翼动力学模型可以求出桨叶的运动和气动载荷,进而计算旋翼的需用功率和桨毂振动水平。再由旋翼气动噪声模型求解噪声,其关系如图 1所示。
|
图 1 旋翼模型关系图 Figure 1 Relations inside rotor model |
1.1.1 翼型气动模型
由于变转速旋翼可能在转速较低的状态下工作,且出于配平的需要后行桨叶将以大迎角进行俯仰运动,从而容易导致动态失速的发生。所以,本文采用Leishman-Beddoes非定常/动态失速模型[14]以更好地体现桨叶微段气动载荷的变化。
模型中的桨叶微段垂向力和俯仰力矩系数包括非定常项Cf与涡诱导项Cv两部分
| $ {C_n}\left( t \right) = C_n^f\left( t \right) + C_n^v\left( t \right) $ | (1) |
| $ {C_m}\left( t \right) = C_m^f\left( t \right) + C_m^v\left( t \right) $ | (2) |
式中:非定常项和涡诱导项为迎角α(t),有效迎角αe(t),迎角俯仰角速度q(t),当地马赫数Ma,后缘分离点f以及前缘涡脱离时间τ的函数
| $ {\alpha _e}\left( t \right) = {\alpha _{\frac{3}{4}}}\left( t \right) - X\left( t \right) - Y\left( t \right) $ | (3) |
| $ f = \left\{ {\begin{array}{*{20}{c}} {1 - 0.3\exp \left( {\frac{{\left( {\alpha - {\alpha _{0.7}}} \right)}}{{{S_1}}}} \right)}&{\alpha \le {\alpha _{0.7}}}\\ {0.04 + 0.66\exp \left( {\frac{{\left( {{\alpha _{0.7}} - \alpha } \right)}}{{{S_2}}}} \right)}&{\alpha > {\alpha _{0.7}}} \end{array}} \right. $ | (4) |
式中:
桨叶微段弦向力系数由Kirchoff理论给出
| $ {C_c}\left( t \right) = \eta {C_\alpha }\left( {Ma} \right){\alpha _e}\left( t \right)\sin {\alpha _e}\left( t \right)f''{\left( t \right)^k} $ | (5) |
| $ k = \left\{ {\begin{array}{*{20}{c}} {0.5}&{{{C'}_n}\left( t \right) \le {C_{nc}}}\\ {0.5{D_f}\left( t \right)\left( {{{C'}_n}\left( t \right) - {C_{nc}}} \right)}&{{{C'}_n}\left( t \right) > {C_{nc}}} \end{array}} \right. $ | (6) |
式中:η为效率系数;Cα(Ma)为翼型的升力线斜率;f″(t)为修正后的后缘分离点;Df(t)为升力延迟项;C′n(t)为延迟后的垂向力系数;Cnc为临界垂向力系数。
最后桨叶微段升力和阻力系数可表示为
| $ {C_L}\left( t \right) = {C_n}\left( t \right)\cos {\alpha _e}\left( t \right) + {C_c}\left( t \right)\sin {\alpha _e}\left( t \right) $ | (7) |
| $ {C_D}\left( t \right) = {C_n}\left( t \right)\sin {\alpha _e}\left( t \right) - {C_c}\left( t \right)\cos {\alpha _e}\left( t \right) + {C_{D0}} $ | (8) |
式中:CD0为零升阻力系数。
1.1.2 旋翼入流模型为了获得桨叶载荷的高阶项以计算出更准确的桨毂振动水平,本文引入Peters-He广义动态入流模型[15]计算桨盘的诱导速度分布。桨盘的量纲一诱导速度分布与动态入流方程如下所示
| $ \begin{array}{*{20}{c}} {{v_i}\left( {\bar r,\psi } \right) = \sum\limits_{m = 0}^\infty {\sum\limits_{n = m + 1,m + 3}^\infty {\frac{{P_n^m\left( {\bar x} \right)}}{{\bar x}}} } \cdot }\\ {\left[ {\alpha _n^m\cos \left( {m\psi } \right) + \beta _n^m\sin \left( {m\psi } \right)} \right]} \end{array} $ | (9) |
| $ \left\{ {\dot \alpha _n^m} \right\} + {\mathit{\boldsymbol{L}}^{ - 1}}\left\{ {\alpha _n^m} \right\} = \frac{1}{2}\left\{ {\tau _n^m} \right\} $ | (10) |
式中:υi为量纲一诱导速度;r为量纲一径向位置;ψ为方位角;m,n为非负整数;
本文根据Hamilton原理[17],采用中等变形梁理论结合有限元方法建立了考虑桨叶挥舞、摆振、扭转和拉伸耦合关系的桨叶动力学方程。用Newmark方法[18]求解桨叶各个离散节点的位移、速度和加速度。
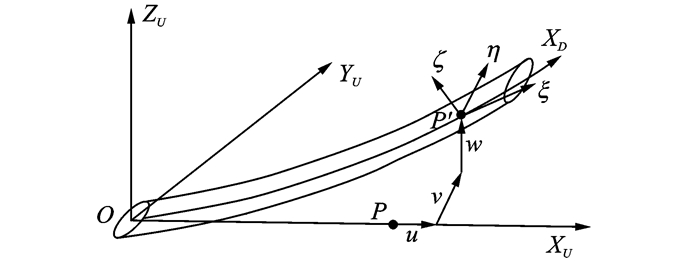
为了得到桨叶应变能、动能和外力虚功,需要定义桨叶的变形坐标系。如图 2所示,桨叶未变形坐标系上的一点P经过弹性变形至P′时所产生的位移量与弹性扭转角为u,v,w,φ。然后经过欧拉角变换完成变形坐标系到未变形坐标系的转换。
|
图 2 桨叶变形坐标系 Figure 2 Blade deformation coordinate |
对桨叶进行有限元离散,每片桨叶离散为n段两节点梁单元。每个节点包含拉伸位移、摆振位移、摆振挠度、挥舞位移、挥舞挠度、扭转角6个自由度
| $ {\mathit{\boldsymbol{q}}^{\rm{T}}} = \left\{ {u,v,v',w,w',\varphi } \right\} $ | (11) |
然后通过Hermite插值多项式表达的形函数和节点位移表示单元内任一点的位移,即可得到质量矩阵M,阻尼矩阵C,刚度矩阵K,载荷向量F和桨叶运动方程,即
| $ \mathit{\boldsymbol{M\ddot q}} + \mathit{\boldsymbol{C\dot q}} + \mathit{\boldsymbol{Kq}} = \mathit{\boldsymbol{F}} $ | (12) |
最后使用Newmark方法求解方程获得桨叶运动状态后即可计算桨毂振动水平。桨根力与力矩通过力积分法获得[19]
| $ {S_z} = \int_{{l_\beta }}^R {{F_\beta } - m\ddot z{\rm{d}}r} $ | (13) |
| $ {S_r} = \int_0^R {{F_r}} + m{\mathit{\Omega }^2}r - 2\mathit{\Omega }\dot xm{\rm{d}}r $ | (14) |
| $ {S_x} = \int_{{l_\zeta }}^R {{F_\zeta } - m\ddot x} + m{\mathit{\Omega }^2}x{\rm{d}}r $ | (15) |
| $ {M_\beta } = \left\{ {\begin{array}{*{20}{c}} {\int_0^R {r\left( {{F_\beta } - m\ddot z - m{\mathit{\Omega }^2}z} \right){\rm{d}}r} }&{无铰式}\\ {{S_z}{l_\beta }}&{铰接式} \end{array}} \right. $ | (16) |
| $ {M_\zeta } = \left\{ {\begin{array}{*{20}{c}} {\int_0^R {r\left( {{F_\zeta } - m\ddot x + m{\mathit{\Omega }^2}x} \right){\rm{d}}r} }&{无铰式}\\ {{S_x}{l_\zeta }}&{铰接式} \end{array}} \right. $ | (17) |
式中:Fβ,Fζ,Fr为桨叶微段的气动力;x,
各片桨叶的桨根力与力矩以傅里叶级数形式展开并转换到非旋转坐标系中求和即可得到桨毂力与力矩的第N次谐波分量
| $ \begin{array}{*{20}{c}} {F_x^{NP} = \sum\limits_{i = 1}^N {S_{ri}^{NP}\cos \left[ {\psi + \left( {i - 1} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{N}} \right]} + }\\ {\sum\limits_{i = 1}^N {S_{xi}^{NP}\sin \left[ {\psi + \left( {i - 1} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{N}} \right]} } \end{array} $ | (18) |
| $ \begin{array}{*{20}{c}} {F_y^{NP} = \sum\limits_{i = 1}^N {S_{ri}^{NP}\sin \left[ {\psi + \left( {i - 1} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{N}} \right]} - }\\ {\sum\limits_{i = 1}^N {S_{xi}^{NP}\cos \left[ {\psi + \left( {i - 1} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{N}} \right]} } \end{array} $ | (19) |
| $ F_z^{NP} = \sum\limits_{i = 1}^N {S_{zi}^{NP}} $ | (20) |
| $ M_x^{NP} = \sum\limits_{i = 1}^N {M_{\beta i}^{NP}\sin \left[ {\psi + \left( {i - 1} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{N}} \right]} $ | (21) |
| $ M_y^{NP} = - \sum\limits_{i = 1}^N {M_{\beta i}^{NP}\cos \left[ {\psi + \left( {i - 1} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{N}} \right]} $ | (22) |
| $ M_z^{NP} = \sum\limits_{i = 1}^N {M_{\zeta i}^{NP}} $ | (23) |
式中:N为桨叶片数;ψ为方位角;上标NP表示该量的第N次谐波成分。
在上述结果的基础上,引入文献[20]中采用的旋翼桨毂振动水平指标计算公式,如式(24)所示。该指标用于表示旋翼桨毂振动水平大小,指标越大说明旋翼桨毂振动水平越大。
| $ J = {10^4}\sqrt {\frac{{\sum {{{\left( {F_{x,y,z}^{NP}} \right)}^2}} }}{{{{\left( {m{\mathit{\Omega }^2}{R^2}} \right)}^2}}} + \frac{{\sum {{{\left( {M_{x,y,z}^{NP}} \right)}^2}} }}{{{{\left( {m{\mathit{\Omega }^2}{R^3}} \right)}^2}}}} $ | (24) |
为了快速求解旋翼气动噪声,本文采用了Farassat发展的求解FW-H方程的时域积分方法[21-23],即Farassat 1A公式。该方法的优点是只需得到旋翼桨叶运动及气动载荷分布即可通过一套统一的计算公式得出旋翼气动噪声,并且方便用于数值计算。Farassat 1A公式为
载荷噪声
| $ \begin{array}{*{20}{c}} {4{\rm{ \mathsf{ π} }}{p_L}\left( {x,t} \right) = \frac{1}{v}\int_{f = 0} {{{\left[ {\frac{{{{\dot l}_i}{{\hat r}_i}}}{{r{{\left( {1 - M{a_r}} \right)}^2}}}} \right]}_{ret}}{\rm{d}}s} + }\\ {\int_{f = 0} {{{\left[ {\frac{{{l_r} - {l_i}M{a_i}}}{{{r^2}{{\left( {1 - M{a_r}} \right)}^2}}}} \right]}_{ret}}{\rm{d}}s} + }\\ {\frac{1}{c}\int_{f = 0} {{{\left[ {\frac{{{l_r}\left( {r\dot M{a_i}{{\hat r}_i} + cM{a_r} - cM{a^2}} \right)}}{{{r^2}{{\left( {1 - M{a_r}} \right)}^3}}}} \right]}_{ret}}{\rm{d}}s} } \end{array} $ | (25) |
厚度噪声
| $ \begin{array}{*{20}{c}} {4{\rm{ \mathsf{ π} }}{p_T}\left( {x,t} \right) = \int_{f = 0} {{{\left[ {\frac{{{\rho _0}{{\dot V}_n}}}{{r{{\left( {1 - M{a_r}} \right)}^2}}}} \right]}_{ret}}{\rm{d}}s} + }\\ {\int_{f = 0} {{{\left[ {\frac{{{\rho _0}{V_n}\left( {r\dot M{a_i}{{\hat r}_i} + cM{a_r} - cM{a^2}} \right)}}{{{r^2}{{\left( {1 - M{a_r}} \right)}^3}}}} \right]}_{ret}}{\rm{d}}s} } \end{array} $ | (26) |
总噪声
| $ p\left( {x,t} \right) = {p_L}\left( {x,t} \right) + {p_T}\left( {x,t} \right) $ | (27) |
式中:被积函数
而声波发射时间和位置通过求解延迟时间方程得到
| $ g = \tau - t + \frac{{\left| \mathit{\boldsymbol{r}} \right|}}{c} = 0 $ | (28) |
式中:τ为噪声发射时间;|r|为发射点到接收点的距离。
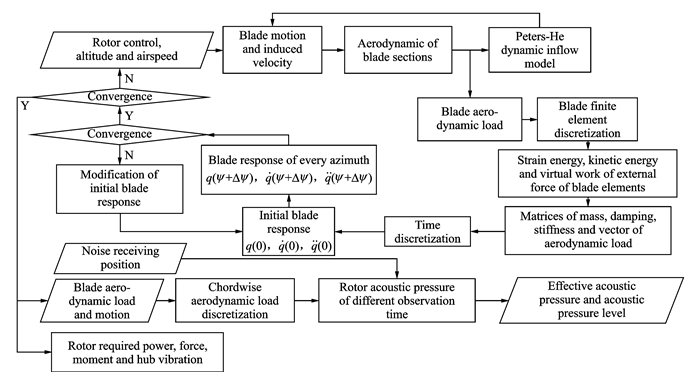
对于整个旋翼模型,其综合计算流程如图 3所示。首先由翼型气动模型、旋翼入流模型与旋翼动力学模型迭代求解旋翼气动力与桨叶运动。由于同时计算旋翼气动力与桨叶运动会使计算量巨大并且难以收敛。本文采取一种松弛耦合的迭代计算方法[24]。在计算旋翼气动力时保持诱导速度与桨叶运动不变。将得出的旋翼气动力与桨叶气动载荷分布作为输入计算旋翼诱导速度和桨叶运动,此时保持旋翼气动力与桨叶气动载荷不变。当桨叶气动载荷、诱导速度和桨叶运动达到动态平衡时结束迭代计算。由此获得当前旋翼操作量、姿态及运动速度下的旋翼气动力和桨叶运动。为了更好地体现桨叶气动载荷与桨叶运动对旋翼气动噪声的影响,旋翼气动模型与旋翼动力学模型都会在收敛后记录下每片桨叶各个方位角、半径处的气动载荷、运动速度与加速度。然后使用旋翼气动噪声模型计算给定接收时间和接收点位置的噪声声压。
|
图 3 旋翼模型计算流程图 Figure 3 Calculation flow of rotor mode |
1.2 其他部件模型
尾桨的气动力模型与旋翼相似,采用叶素法计算气动力。直升机飞行速度、角速度、旋翼尾迹和机身尾迹的干扰都对尾桨处的相对来流速度有影响,如式(29)所示
| $ \left\{ {\begin{array}{*{20}{c}} {{u_{TR}} = {u_b}{k_{QTR}} - {q_b}{z_{TR}} + {r_b}{y_{TR}} + {u_{iTR}}}\\ {{v_{TR}} = {v_b}{k_{QTR}} + {p_b}{z_{TR}} - {r_b}{x_{TR}} + {v_{iTR}}}\\ {{w_{TR}} = {w_b}{k_{QTR}} - {p_b}{y_{TR}} + {q_b}{x_{TR}} + {w_{iTR}}} \end{array}} \right. $ | (29) |
式中:ub,vb,wb为机体速度;kQTR为动压损失系数;pb,qb,rb为机体重心角速度;xTR,yTR,zTR为尾桨中心到机体重心的距离;uiTR,viTR,wiTR为旋翼/机身尾迹对尾桨的干扰速度,该速度依据气动干扰试验结果确定旋翼/机身尾迹对尾桨处速度的影响。而后文用到的干扰速度都是采用该方法确定的,后面不再赘述。
尾桨入流采用均匀入流模型计算。结合尾桨总距与尾桨负扭可以得到叶素的迎角。据此通过尾桨翼型的风洞试验数据可差值计算桨叶微段的气动载荷,进而可积分出尾桨气动力。
机身的气动力与力矩也通过风洞试验数据差值计算,其相对来流速度为
| $ \left\{ {\begin{array}{*{20}{c}} {{u_F} = {u_b} + {u_{iF}}}\\ {{v_F} = {v_b} + {v_{iF}}}\\ {{w_F} = {w_b} + {w_{iF}}} \end{array}} \right. $ | (30) |
式中:uiF,viF,wiF为旋翼尾迹对机身的干扰速度。
由此可得机身迎角、侧滑角与动压,并最终得到当前飞行状态下的机身气动力与力矩。
平尾处的来流速度如式(31)所示。通过此速度和平尾安装角可得到平尾的动压和迎角,进而差值计算出气动力与力矩。
| $ \left\{ {\begin{array}{*{20}{c}} {{u_H} = {u_b}{k_{QH}} - {q_b}{z_H} + {r_b}{y_H} + {u_{iH}}}\\ {{v_H} = {v_b}{k_{QH}} + {p_b}{z_H} - {r_b}{x_H} + {v_{iH}}}\\ {{w_H} = {w_b}{k_{QH}} - {p_b}{y_H} + {q_b}{x_H} + {w_{iH}}} \end{array}} \right. $ | (31) |
式中:kQH为动压损失系数;xH,yH,zH为平尾到机体重心的距离;uiH,viH,wiH为旋翼和机身尾迹对平尾的干扰速度。
垂尾模型与平尾类似,其来流速度为
| $ \left\{ {\begin{array}{*{20}{c}} {{u_V} = {u_b}{k_{QV}} - {q_b}{z_V} + {r_b}{y_V} + {u_{iV}}}\\ {{v_V} = {v_b}{k_{QV}} + {p_b}{z_V} - {r_b}{x_V} + {v_{iV}}}\\ {{w_V} = {w_b}{k_{QV}} - {p_b}{y_V} + {q_b}{x_V} + {w_{iV}}} \end{array}} \right. $ | (32) |
式中:kQV为动压损失系数;xV,yV,zV为垂尾到机体重心的距离;uiV,viV,wiV为旋翼和机身尾迹对垂尾的干扰速度。
1.3 模型配平如图 4所示,上述各部件模型计算出给定飞行状态下该部件的气动力与力矩后代入全机平衡方程中判断是否满足平衡条件。若不满足则通过牛顿迭代法求出新的操纵量和姿态角,再进行新一轮迭代计算,直至收敛[25]。全机平衡方程包括纵向、横向和航向的力平衡,以及俯仰、滚转力矩和反扭矩的平衡,方程如式(33)所示。
| $ \left\{ {\begin{array}{*{20}{c}} {{F_{xR}} + {F_{xF}} + {F_{xTR}} + {F_{xH}} + {F_{xV}} - G\sin \vartheta = 0}\\ {{F_{yR}} + {F_{yF}} + {F_{yTR}} + {F_{yH}} + {F_{yV}} - G\cos \vartheta \cos \gamma = 0}\\ {{F_{zR}} + {F_{zF}} + {F_{zTR}} + {F_{zH}} + {F_{zV}} + G\cos \vartheta \sin \gamma = 0}\\ {{M_{xR}} + {M_{xF}} + {M_{xTR}} + {M_{xH}} + {M_{xV}} = 0}\\ {{M_{yR}} + {M_{yF}} + {M_{yTR}} + {M_{yH}} + {M_{yV}} = 0}\\ {{M_{zR}} + {M_{zF}} + {M_{zTR}} + {M_{zH}} + {M_{zV}} = 0}\\ {p + q\sin \gamma \tan \vartheta + r\cos \gamma \tan \vartheta = 0}\\ {q\cos \gamma - r\sin \gamma = 0}\\ {q\sin \gamma \sec \vartheta + r\cos \gamma \sec \vartheta = 0} \end{array}} \right. $ | (33) |

|
图 4 综合分析方法计算流程 Figure 4 Calculation flow of comprehensive analysis mode |
式中:FxR,FyR,FzR,MxR,MyR,MzR为旋翼力与力矩;FxF,FyF,FzF,MxF,MyF,MzF为机身力与力矩;FxTR,FyTR,FzTR,MxTR,MyTR,MzTR为尾桨力与力矩;FxH,FyH,FzH,MxH,MyH,MzH为平尾力与力矩;FxV,FyV,FzV,MxV,MyV,MzV为垂尾力与力矩;G为总重力;γ,
完成配平计算后既可得到直升机在稳定飞行状态下的旋翼需用功率、全机配平操纵、旋翼桨毂振动水平和旋翼气动噪声。
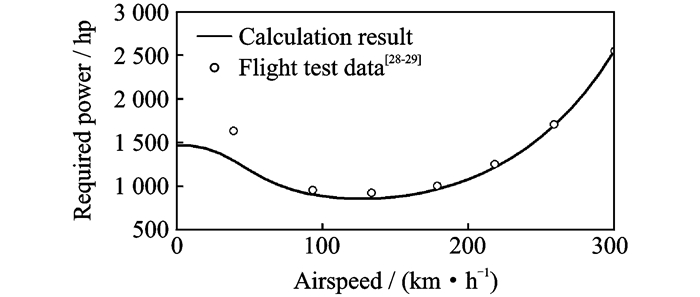
2 模型验证本文把UH-60A“黑鹰”直升机作为样例直升机以验证本文直升机综合分析模型的准确性。其基本参数和桨叶结构参数分别取自文献[26, 27],而飞行试验配平结果取自文献[28, 29]。图 5,6为本文模型配平计算得到的旋翼需用功率、操纵量、飞行姿态和飞行试验数据[28-29]的对比图。从图中可看出本文的计算结果与飞行试验数据吻合良好。在小速度情况下的计算需用功率,总距操纵量和飞行试验结果存在较大差异,而对应速度下的尾桨脚蹬操纵量没有出现与总距相应的偏差均因为在飞行试验中或多或少存在着风速的影响。风速在直升机低速飞行时的影响较大,所以低速状态的配平计算与飞行试验数据有较大差别。而且直升机在低速飞行时,飞行员较难保持配平状态,同样会带来计算结果与飞行数据间的差别[26]。但总体而言,本文模型计算的旋翼需用功率与全机配平特性满足分析需要。
|
图 5 直升机综合分析方法旋翼需用功率验证 Figure 5 Rotor required power and validation of helicopter comprehensive analysis model |

|
图 6 直升机综合分析方法配平结果验证 Figure 6 Trim result and validation of helicopter comprehensive analysis model |
表 1为UH-60A桨叶在100%转速下前7阶固有频率。本文模型计算结果与文献[30]计算结果吻合,最大误差只有3.33%。
| 表 1 桨叶固有频率(总距14.5°) Table 1 Blade frequency(Collective pitch 14.5°) |
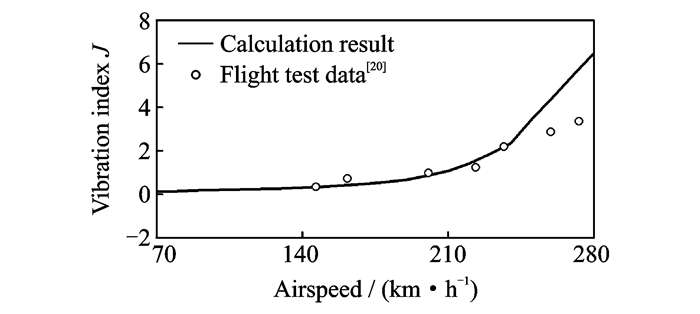
图 7为本文模型与文献[20]中使用GENHEL直升机分析软件在相同条件下得出的旋翼桨毂振动水平指标的对比图。图中结果表明两模型计算结果相符,且趋势一致。其中在大速度情况下出现的差异是旋翼气动模型不同引起的。综合判断综合分析模型的旋翼动力学计算精度满足要求。
|
图 7 直升机综合分析方法旋翼桨毂振动水平验证 Figure 7 Rotor hub vibration index and validation of helicopter comprehensive analysis model |
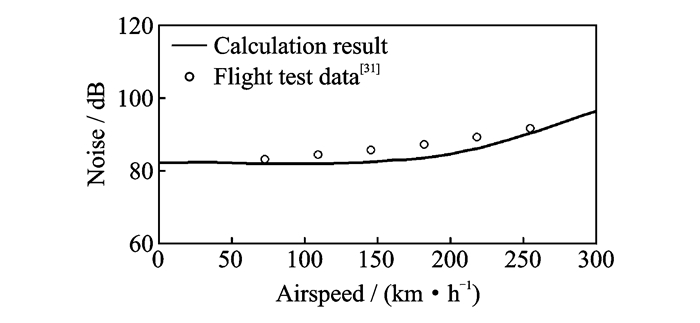
最后是验证旋翼气动噪声模型。本文验证直升机水平前飞时,位于旋翼正下方152.4 m处接收点的噪声。计算结果与取自文献[31]的飞行实测噪声的对比如图 8所示,两者基本一致。说明本文综合分析模型的旋翼气动噪声计算可信,可以用于直升机旋翼气动噪声的分析。
|
图 8 直升机综合分析方法旋翼噪声验证 Figure 8 Rotor noise and validation of helicopter comprehensive analysis model |
综上所述,本文综合分析模型的准确性满足要求。说明该模型可以用于进一步的分析研究。
3 综合分析旋翼转速作为直升机的总体设计参数,其变化将同时引起多方面的影响。本文应用上述建立的直升机综合分析模型对UH-60A“黑鹰”直升机旋翼转速变化引起的影响进行综合分析。本文采用的分析策略为计算不同旋翼转速下直升机的旋翼需用功率、全机配平操纵、旋翼桨毂振动水平和旋翼气动噪声随前飞速度的变化。然后根据上述特性的变化趋势展开分析。表 2为计算设置。
| 表 2 计算设置 Table 2 Overall settings |
3.1 旋翼需用功率与配平操纵量
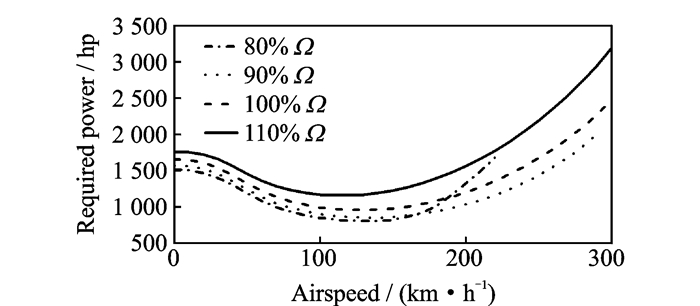
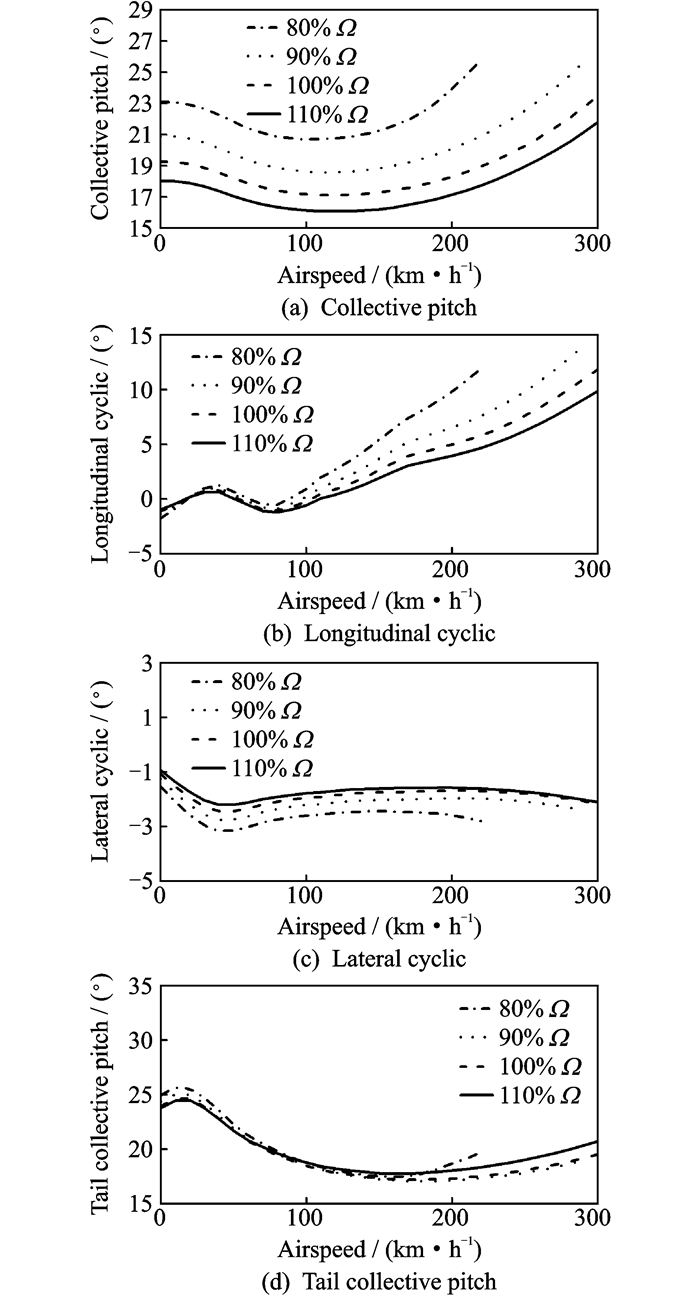
图 9为旋翼需用功率随飞行速度的变化曲线。由图 9可知,旋翼需用功率在大部分飞行状态下都随着旋翼转速降低而减小,而为了保持拉力,随着旋翼转速降低旋翼总距要相应地提高,让更多的桨叶段在大升/阻比迎角下工作,如图 10(a)所示。同时降低转速引起的前进比增加会导致桨盘前/后行桨叶的动压不对称性增加,从而使桨盘后倒。桨盘后倒角增加与旋翼转速降低引起的锥度角增加会造成桨盘前/后半圆中桨叶的迎角不对称性增加,最终造成桨盘侧倒。因此,为了保持配平状态,纵/横向周期变距都随着旋翼转速的降低而增加,如图 10(b,c)所示。所以过低的旋翼转速会使直升机无法配平。图中80%转速的曲线在约220 km/h的前飞速度处终止,说明配平对旋翼转速的变化有限制作用。此外,纵向周期变距的斜率也随着旋翼转速降低而增加,说明其的功效会随着旋翼转速降低而降低。但旋翼转速的变化对尾桨总距影响很小,如图 10(d)所示。
|
图 9 旋翼需用功率随飞行速度的变化曲线 Figure 9 Rotor required power vs. airspeed |
|
图 10 配平操纵量随飞行速度的变化曲线 Figure 10 Trim controls vs. airspeed |
3.2 桨叶固有频率与旋翼桨毂振动水平
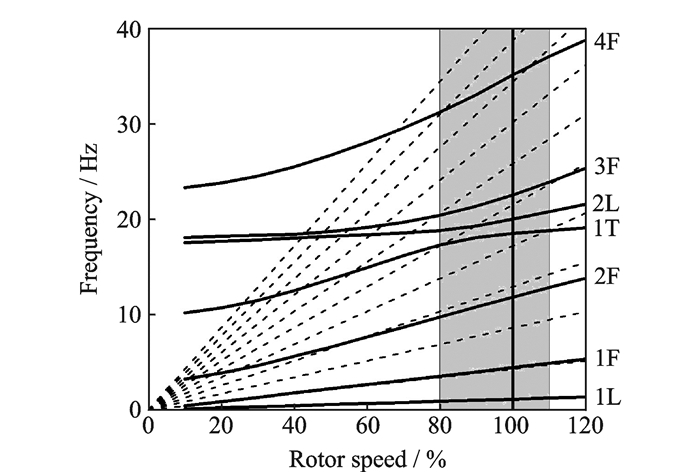
图 11为UH-60A桨叶共振图。图中右侧的注释1L,1F,1T分别表示一阶摆振,一阶挥舞和一阶扭转频率,以此类推。其中灰色区域为本文研究的旋翼转速变化范围,该区域内共振点较少。在设计旋翼转速时应避开共振点,并且当旋翼转速变化时应尽快地通过共振点。
|
图 11 桨叶共振图 Figure 11 Blade frequency in vacuum |
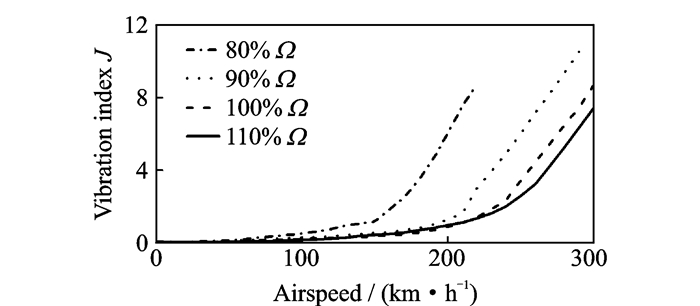
不同旋翼转速下的旋翼桨毂振动水平随前飞速度的变化如图 12所示。旋翼桨毂振动水平呈现出随着旋翼转速下降而增大的趋势。其主要原因是,随着前飞速度增加桨盘前/后行桨叶的动压不对称性加剧,导致桨盘升/阻力分布越来越不均匀。旋翼以80%转速工作时,桨叶更早地引发动态失速导致桨毂振动水平更早开始明显地增加。
|
图 12 桨毂振动水平随飞行速度的变化曲线 Figure 12 Hub vibration index vs. airspeed |
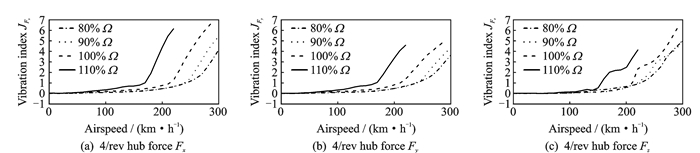
图 13,14给出了不同旋翼转速下旋翼桨毂力和力矩的量纲为一的4次谐波成分(量纲一方式与式(24)相同)随前飞速度的变化曲线。从各图中可得出:
|
图 13 桨毂力4次谐波成分随飞行速度的变化曲线 Figure 13 4/rev vibratory hub forces vs. airspeed |

|
图 14 桨毂力矩4次谐波成分随飞行速度的变化曲线 Figure 14 4/rev vibratory hub moments vs. airspeed |
(1) 速度较小时,3个方向的力都随飞行速度增加而缓慢增加,到达一定前飞速度后则开始迅速增加。
(2) 桨毂力开始迅速增加的飞行速度随着旋翼转速的增加而变大。
(3) Fx,Fy随旋翼转速与前飞速度变化的趋势一致。
(4) Fz对旋翼转速的敏感度小于Fx与Fy。
(5) 桨毂力矩随着前飞速度的增加有所增加,但不明显。
以上,说明了样例直升机的旋翼桨毂振动水平的增加主要来自于桨毂上3个方向的力的变化。而且旋翼转速较低时,Fx与Fy的影响较大;随着旋翼转速增加,Fz的影响逐渐增加。桨毂力矩较小且变化不明显是由于样例直升机采用了铰接式旋翼。
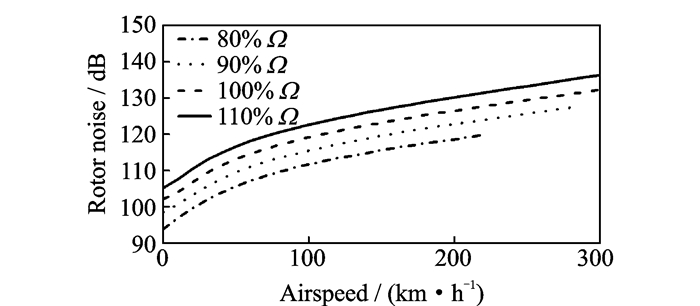
3.3 旋翼气动噪声在不同的旋翼转速下,桨盘平面内位于桨毂坐标系(2R, 2R, 0)处接收点的总旋翼气动噪声随前飞速度的变化如图 15所示。图中所示表明旋翼气动噪声随着前飞速度增加而增加,随着旋翼转速降低而降低。
|
图 15 旋翼气动噪声随飞行速度的变化曲线 Figure 15 Rotor noise vs. airspeed |
总旋翼气动噪声包含了载荷噪声与厚度噪声量部分,其中载荷噪声的变化趋势如图 16(a)所示。当前飞速度较小时,载荷噪声随着旋翼转速增加的变化不明显。可当前飞速度超过某一值后,载荷噪声开始迅速增加,而且该情况在旋翼转速过小或过大时更为明显。因为工作在大转速下的前行桨叶会受到压缩效应影响更早地产生激波,使得旋翼气动载荷变化剧烈,导致载荷噪声迅速增加。类似地,转速过小时,工作在大总距下的后行桨叶容易引发动态失速,同样造成旋翼气动载荷变化剧烈。另一方面,厚度噪声在各前飞速度下都随着旋翼转速降低而减小,如图 16(b)所示。这是桨叶相对空气的运动速度随着旋翼转速降低而减小所致。对比两者可发现厚度噪声对总旋翼气动噪声的贡献大于载荷噪声,因此总旋翼气动噪声会更多的体现出厚度噪声的变化趋势。
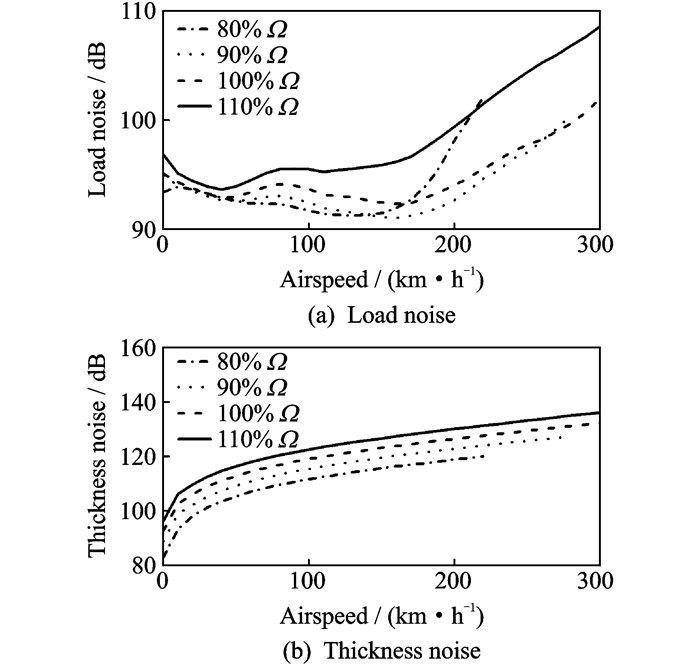
|
图 16 旋翼载荷噪声与厚度噪声随飞行速度的变化曲线 Figure 16 Rotor load noise and thickness noise vs. airspeed |
通过图 9,10,12,15可从旋翼需用功率、全机配平操纵、旋翼桨毂振动水平和旋翼气动噪声4方面综合分析旋翼转速变化所带来的影响。首先,当样例直升机以100 km/h以下的小速度前飞时,旋翼需用功率和气动噪声都随着旋翼转速下降而减小。在这速度范围内,相对于100%旋翼转速,80%旋翼转速下的旋翼需用功率和气动噪声分别最多减小了16.9%和6.7%。同时总距的增加在该范围内也最为明显。而旋翼桨毂振动水平虽随转速下降的变化不明显,但也在缓慢地增大。其次,在100~200 km/h的中等前飞速度下,旋翼需用功率和气动噪声基本延续小前飞速度时的变化规律。并且通过降低旋翼转速旋翼需用功率在140 km/h的前飞速度下获得19.2%的最大减小量,而此时旋翼气动噪声的减小量为6.57%。但在80%旋翼转速下,旋翼需用功率在前飞速度超过170 km/h时开始迅速增加。此前飞速度范围下还能明显地观察到旋翼的纵向周期变距和旋翼桨毂振动水平都随着旋翼转速的降低而迅速增加。最后,在200 km/h以上的大前飞速度状态下,最小旋翼转速不再对应着最小旋翼需用功率。最小旋翼需用功率所对应的旋翼转速需通过实际飞行状态计算得出。旋翼总距、纵/横向周期变距及旋翼桨毂振动水平则随着旋翼转速降低进一步地迅速增大。而旋翼气动噪声还是保持着与旋翼转速的正比关系。
4 结论(1) 本文建立了适用于变转速旋翼直升机的综合分析模型,通过与UH-60A“黑鹰”直升机的飞行试验数据及相关研究结果的对比,表明该方法可用于综合分析直升机稳态飞行时的旋翼需用功率、全机配平操纵、旋翼桨毂振动水平与旋翼气动噪声。
(2) 旋翼需用功率与旋翼转速在一定转速和前飞速度范围内成正比关系。降低旋翼转速可使样例直升机在上述飞行状态下最多减少19.2%的需用功率。但当因转速过小、前飞速度过大而需要大总距配平时会导致旋翼需用功率迅速增加。
(3) 旋翼转速减小会导致旋翼总距、纵向周期变距和横向周期变距增加,从而使直升机旋翼的操纵裕度减小。同时旋翼纵向周期变距的功效随着旋翼转速的减小而下降。
(4) 旋翼桨毂振动水平在各前飞速度下都随着旋翼转速降低而增加,而且该效果在大前飞速度下更为明显。
(5) 旋翼气动噪声随着旋翼转速降低而减小,其中厚度噪声的减小起主要作用。在当前飞行状态下通过降低旋翼转速使旋翼气动噪声最多降低了6.7%。但过大或过小的旋翼转速都会使得旋翼载荷噪声随着前飞速度增加而迅速增加。
综上所述,在稳定飞行状态下直升机可以通过降低旋翼转速显著地提升飞行性能和降低旋翼气动噪声。但是在调整转速的过程中还需要考虑旋翼操纵量和旋翼桨毂振动的约束。
| [1] |
PROUTY R W.
Should we consider variable rotor speeds[J]. Vertiflite, 2004, 50(4): 24–27.
|
| [2] |
BOWEN-DAVIS G, CHOPRA I.
Aeromechanics of a slowed rotor[J]. Journal of the American Helicopter Society, 2015, 60(3): 1–13.
|
| [3] |
DIOTTAVIO J, FRIEDMANN D. Operational benefits of an optimal, widely variable speed rotor[C]//Proceedings of the American Helicopter Society 66th Annual Forum. Phoenix, AZ: [s.n.], 2010: 1011-1017. |
| [4] |
BOWEN-DAVIS G, CHOPRA I. Aeromechanics of a variable-speed rotor[C]//Proceedings of the American Helicopter Society 67th Annual Forum. Virginia Beach, Virginia: [s.n.], 2011. |
| [5] |
韩东.
变转速旋翼直升机性能及配平研究[J]. 航空学报, 2013, 34(6): 1241–1248.
HAN Dong. Study on the performance and trim of helicopters with variable speed rotors[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1241–1248. |
| [6] |
刘士明, 杨卫东, 董凌华, 等.
优化转速旋翼性能分析与应用[J]. 南京航空航天大学学报, 2014, 46(6): 888–894.
DOI:10.3969/j.issn.1005-2615.2014.06.011 LIU Shiming, YANG Weidong, DONG Linghua, et al. Performance investigation and applications of optimum speed rotors[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(6): 888–894. DOI:10.3969/j.issn.1005-2615.2014.06.011 |
| [7] |
徐明, 李建波, 韩东.
旋翼转速优化直升机的纵向操纵性与稳定性分析[J]. 航空动力学报, 2015, 30(6): 1374–1381.
XU Ming, LI Jianbo, HAN Dong. Analyze on longitudinal controllability and stability of OSR helicopter[J]. Journal of Aerospace Power, 2015, 30(6): 1374–1381. |
| [8] |
徐明, 韩东, 李建波.
变转速旋翼气动特性分析及试验研究[J]. 航空学报, 2013, 34(9): 2047–2056.
XU Ming, HAN Dong, LI Jiangbo. Analysis and experimental investigation on the aerodynamic characteristics of variable speed rotor[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2047–2056. |
| [9] |
徐明, 李建波, 韩东.
转速优化旋翼的桨叶气动外形参数优化设计[J]. 航空学报, 2015, 36(7): 2133–2144.
XU Ming, LI Jiangbo, HAN Dong. Optimal design for aerodynamic shape parameters of optimum speed rotor[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2133–2144. |
| [10] |
徐明, 李建波, 彭名华, 等.
基于不确定性的旋翼转速优化直升机参数设计[J]. 航空学报, 2016, 37(7): 2170–2179.
XU Ming, LI Jiangbo, PENG Minghua, et al. Parameter design of helicopter with optimum speed rotor based on uncertainty optimization[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2170–2179. |
| [11] |
DATTA A, YEO H, NORMAN T R. Experimental investigation and fundamental understanding of a slowed UH-60A rotor at high advance ratios[C]//Proceedings of the American Helicopter Society 67th Annual Forum. Virginia Beach, Virginia: [s.n.], 2011: 1105-1130. |
| [12] |
BERRY B, CHOPRA I. Performance and vibratory load measurements of a slowed-rotor at high advance ratios[C]//Proceedings of the 68th Annual Forum of the American Helicopter Society. Fort Worth, Texas: [s.n.], 2012. |
| [13] |
KAREM A E. Optimum speed rotor: U.S. Patent 6007298[P]. 1999-12-28. |
| [14] |
LEISHMAN J G, BEDDOES T S.
A semi-empirical model for dynamic stall[J]. Journal of the American Helicopter Society, 1989, 34(3): 3–17.
DOI:10.4050/JAHS.34.3
|
| [15] |
徐进, 孙传伟, 高正.
适用于直升机俯仰与滚转机动分析的广义动态尾迹模型[J]. 南京航空航天大学学报, 2005, 37(2): 135–139.
DOI:10.3969/j.issn.1005-2615.2005.02.001 XU Jin, SUN Chuanwei, GAO Zheng. Generalized dynamic wake model applied to helicopter pitching and rolling maneuver[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2005, 37(2): 135–139. DOI:10.3969/j.issn.1005-2615.2005.02.001 |
| [16] |
PETERS D A, HE C J.
Finite state induced flow models. Ⅱ-Three-dimensional rotor disk[J]. Journal of Aircraft, 2015, 32(32): 323–333.
|
| [17] |
HODGES D H, DOWELL E H. Nonlinear equations of motion for the elastic bending and torsion of twisted non-uniform rotor blades[R]. NASA TN D-7818, 1974. |
| [18] |
王浩文, 郑兆昌.
前飞状态下直升机旋翼系统气弹响应及稳定性分析[J]. 振动工程学报, 1999, 12(4): 521–528.
WANG Haowen, ZHENG Zhaochang. Aeroelastic response and stability of helicopter rotor blades in forward flight[J]. Journal of Vibration Engineering, 1999, 12(4): 521–528. |
| [19] |
JOHNSON W.
Helicopter theory[M]. New Jersey: Princeton University Press, 1980.
|
| [20] |
MATTHEW A S. Trim and control optimization of a compound helicopter model[D]. Philadelphia: The Pennsylvania State University, 2003. |
| [21] |
FARASSAT F. Thickness noise of helicopter rotors at high tip speeds[R]. AIAA Paper 75-453, 1975. |
| [22] |
FARASSAT F.
Linear acoustic formulas for calculation of rotating blade noise[J]. AIAA Journal, 1981, 19(19): 1122–1130.
|
| [23] |
徐国华.直升机旋翼噪声分析及估算方法[D].南京: 南京航空航天大学, 1990.
|
| [24] |
LI Pan, CHEN Renliang.
A mathematical model for helicopter comprehensive analysis[J]. Chinese Journal of Aeronautics, 2010, 23(3): 41–47.
|
| [25] |
陈仁良, 李攀, 吴伟, 等.直升机飞行动力学数学建模问题[ EB/OL].(2017-04-19). http://kns.cnki.net/kcms/detail/11.1929.V.20170419.1124.002.html.
|
| [26] |
HOWLETT J J. UH-60A Black Hawk engineering simulation program. Volumes I and Ⅱ[R]. NASA CR-166309 and CR-166310, 1981. |
| [27] |
DAVIS S J.Predesign study for a modem 4-bladed rotor for the RSRA[R]. NASA-CR-166155, 1981. |
| [28] |
BALLIN M G. Validation of a real-time engineering simulation of the UH-60A helicopter[R]. NASA-TM-88360, 1987. |
| [29] |
WILLIAM Y A, RANDALL G O, JOHN O B, et al. Validation flight test of UH-60A for rotorcraft systems integration simulator (RSIS)[R]. Project NO. 79-24, 1982. |
| [30] |
ABHISHEK A, DATTA A, CHOPRA I.
Prediction of UH60A structural loads using multibody analysis and swashplate dynamics[J]. Journal of Aircraft, 2009, 46(2): 474–490.
DOI:10.2514/1.35076
|
| [31] |
SCHOMER P D, AVERBUCH A, RASPET R. Operational noise data for UH-60A and CH-47C army helicopters[R]. ADA118796, 1982. |
 2018, Vol. 50
2018, Vol. 50


