2. 91899部队,葫芦岛,125001
2. 91899 Unit, Huludao, 125001, China
飞机结构健康监测技术可实现对飞行器结构损伤的产生与发展,结构健康状态及飞机结构寿命进行在线的监测与预报,对保证飞行安全具有重大的意义和实际的应用价值[1-5]。针对平板类结构件,基于Lamb波的主动结构损伤监测是一种有效的手段。损伤成像作为该方法的重要组成部分,在损伤监测研究中得到了广泛的重视。
目前国内外研究者发展了多种基于Lamb波的损伤成像方法,主要有椭圆(双曲线)成像法、偏移法、时间反转法及相控阵法等[6-12]。袁慎芳等详细介绍了椭圆定位法的基本原理[1];严刚等将地球物理领域的偏移技术引入到结构损伤监测中,提出了基于频率-波数域偏移方法的板结构损伤成像方法[7];张望等采用时间反转技术对声发源源进行了定位[8];孙亚杰等采用相控阵及直方图匹配的方法对成像质量进行了增强处理[9];Gangadharan等结合时间反转法,分别采用宽带及窄带激励,实现了损伤的定位[10];Chen等测量了不同外力下的Lamb波信号,并分别进行了延时叠加成像处理,确定了损伤的位置[11]。这些方法均可实现损伤的定位,但在多组传感器的融合过程中,目前常用的只有简单的全加法和全乘法,即将每组传感路径获得损伤位置信息与其他组信息在每个像素点上直接相加或相乘,以此进行多传感器信息融合[12]。目前采用的全加算法与全乘算法相比,全乘算法具有成像对比度高的特点,而全乘算法易因部分时延确定失准而造成定位误差增大[12-13]。
D-S证据理论是一套基于“证据”和“组合规则”来处理不确定推理问题的数学方法,又称为D-S证据理论。该方法可以在不需要先验概率的条件下,可直接表述“不确定”和“不知道”的能力。对于主动线性Lamb波健康监测方法,在获得了单组传感路径的位置信息后,板中的离散点发生损伤的可能性也可以理解为一种不确定的问题。对于多组传感路径中同一离散点,可能会出现多种不同的损伤发生概率。因此,使得基于D-S证据理论的数据融合方法应用于Lamb波的结构健康监测中成为了可能。但传统的Dempster证据合成法则在处理证据冲突方面存在较多的不足,且可能出现完全偏离真实结果的情况。学者们在改善证据组合规则方面进行了大量的研究,可有效地改善证据冲突对融合结论的影响[14-19]。
在保证多传感器定位成像对比度的情况下,为提高定位系统的可靠度,本文首先分析了传统的比例冲突再分配(Proportional conflict redistribution, PCR)证据融合法则[20],并充分考虑了证据的可信度,采用信号频带局部能量变化的方法,确定了证据的权重值,对传统的PCR证据融合法则进行了加权处理,提出了一种基于加权P CR的证据融合Lamb波损伤成像方法,并通过试验对该方法在定位精度及应对部分路径定位失准方面的优势进行了验证。
1 Lamb波理论Lamb波是自由板中产生的平面应变波,目前是健康监测领域较为可行的方法之一。Lamb波可划分为对称模态和反对称模态。各种模态对应有不同的群速度和相速度,群速度是几个频率相近的谐波叠加到一起形成波包的波包速度,而相速度则是特定频率下的谐波在传播时的速度。目前基于Tof(信号飞行时间)的Lamb波结构健康监测,确定信号模态的群速度及相速度极为关键。Lamb波的群速度及相速度可通过实验实测得到,也可根据Rayleigh-Lamb波方程得到,即
| $ \frac{{\tan \left( {qh} \right)}}{{\tan \left( {qh} \right)}} = - \frac{{4{k^2}pq}}{{{{\left( {{q^2} - {k^2}} \right)}^2}}}\;\;{\rm{对称模态}} $ | (1) |
| $ \frac{{\tan \left( {qh} \right)}}{{\tan \left( {qh} \right)}} = - \frac{{{{\left( {{q^2} - {k^2}} \right)}^2}}}{{4{k^2}pq}}\;\;{\rm{反对称模态}} $ | (2) |
式中:
相速度cp与波长λ的关系及群速度cg与相速度cp的关系为
| $ {c_{\rm p}} = \left( {\frac{\omega }{{2\pi }}} \right)\lambda $ | (3) |
| $ {c_{\rm{g}}} = c_{\rm{p}}^2{\left[ {{c_{\rm{p}}} - \left( {fd} \right)\frac{{{\rm d}{c_{\rm{p}}}}}{{{\rm{d}}\left( {fd} \right)}}} \right]^{ - 1}} $ | (4) |
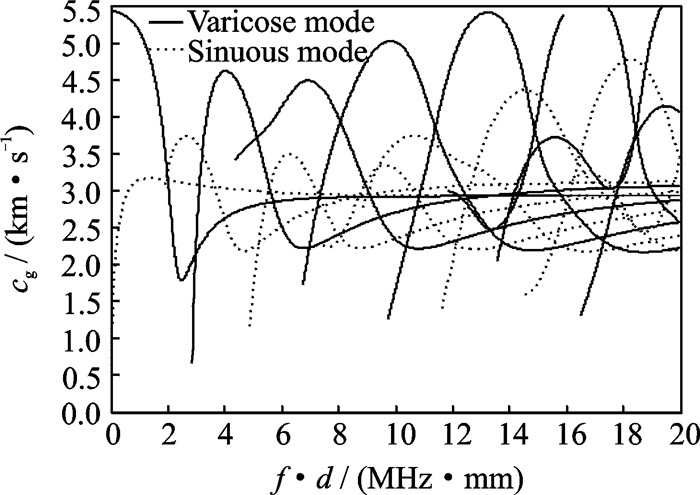
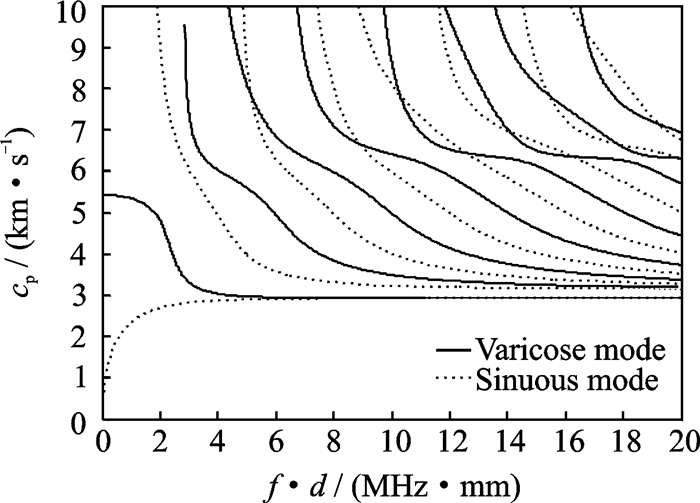
采用二分法,通过MATLAB编程对2A12铝合金板的频散曲线进行了数值求解,其弹性模量为73 GPa,密度为2 780 kg/m3,泊松比为0.33,并绘制了群速度频散曲线和相速度频散曲线(图 1,2)。
|
图 1 群速度频散曲线 Figure 1 Dispersion curve of group speed |
|
图 2 相速度频散曲线 Figure 2 Dispersion curve of phase speed |
从图 1,2中可以看到,随着频率和板厚乘积的变化,Lamb波会激发出不同的模态,因不同模态的群速度和相速度不同,所以随着Lamb波传播时间的增大,其时域的波形发生变化。因此,直接基于时间域信号包络的方法确定时间延迟可能会发生误判。
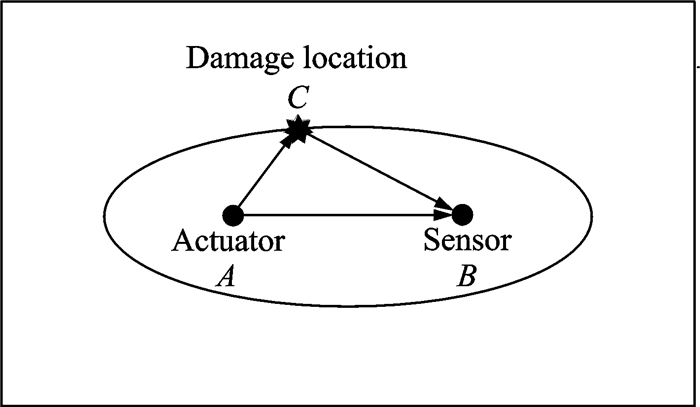
2 椭圆定位方法椭圆定位法是目前基于参考信号的主动监测方法中常用的定位方法。其主要思路是:采用驱动器A在板的表面主动激发Lamb波信号,同时用传感器B在板的其他位置接收结构响应信号,则传感器B接收到的信号是由两部分组成,一部分是由驱动器A激发的直达波信号,另一部分则是由驱动器A激发,经由C到达B的散射波信号。首先,针对健康结构,由传感器B获得健康信号S1;结构发生损伤后,再次测量,获得检测信号S2。根据惠更斯原理,其差信号S3=S2-S1即为损伤的散射信号。由健康信号S1可获得由A直达B的信号飞行时间t1,由差信号S3可得到信号从驱动器A激发,经由损伤C到达B所用的信号飞行时间t2,则时间延迟的即可定义为Δt=t2-t1。已知信号传播的群速度为cg,则根据几何关系可有
| $ L = AC + CB = \Delta t{c_{\rm{g}}} + AB $ | (5) |
式中L为损伤到两传感器的距离之和。
根据式(5) 可知,损伤点C位于以A,B为焦点、到焦点距离之和为Δtcg+AB的椭圆上。因一对传感器只能确定一个椭圆,无法实现损伤定位,故需3个以上的传感器,才可以实现损伤的定位。
|
图 3 椭圆定位法示意图 Figure 3 Schematic of ellipse localization method |
3 基于证据融合理论的损伤成像 3.1 D-S证据理论基础
设U表示所要论证的目标X所组成的论域集合,且U内的所有元素是互不相容的,则称U为X的辨识框架[18]。关于D-S证据理论有以下定义:
定义1 设U为一辨识框架,则函数m:2U→[0, 1],满足以下条件:(1) m(φ)=O;(2)
定义2 设U为一辨识框架,函数m: 2U→[0, 1]为U上的基本可信度分配函数,定义信度函数Bel:2U→[0, 1]为Bel(A) =
定义3 设U为一辨识框架,∀A⊂U,且m(A)>0,则称A为函数Bel的焦元。
定义4 设U为一辨识框架,定义Pl:2U→[0, 1],有:Pl(A)=1-Bel(B),称为似真度函数,Pl(A)为不否定A的信任程度,又称为拟信度。
3.2 Dempster证据合成法则定义5 设m1, m2, m3, …, mk为辨识框架下的k个基本可信度分配函数,同时有miw(U)=1-
| $ m\left( A \right) = {m_1}\left( A \right) \oplus {m_2}\left( A \right) = \frac{{\sum\limits_{{A_i} \cap {B_j} = A} {{m_1}\left( {{A_i}} \right){m_2}\left( {{B_j}} \right)} }}{{1 - K}} $ | (6) |
| $ K = \sum\limits_{{A_i} \cap {B_j} = \varphi } {{m_1}\left( {{A_i}} \right){m_2}\left( {{B_j}} \right)} < 1 $ | (7) |
式中K为整体冲突。当满足式(7) 时,可采用式(6) 进行数据融合。
3.3 改进的加权证据融合法则本文在采用原始的Dempster证据合成法则进行数据融合时发现,虽然通过阈值化处理,可以较为准确地确定损伤位置,但图像成像的对比度较低,不利于直观观察。分析发现,图像分辨率差的主要原因是证据在融合时会存在冲突证据,进而导致分辨率差,甚至定位不准等现象。
目前解决证据冲突的组合法则有:Smets法则、Yager法则、Dubosie-Prade法则、广义加权操作、加权平均操作、minc法则及PCR法则等[20]。PCR融合法则[21]是较为方便有效的方法。又因差信号能量的大小,可能导致部分传感路径时间延迟判断失准,所以本文引入证据权值w=[w1, w2, …, wn],用以降低可能出现时间延迟判断失准路径对损伤成像的贡献,进而提高成像的可靠度。
PCR融合法则的基本思想是将整体冲突按照证据源bbm矩阵中相应列之和的比分配到所有U的非零集合中。由两个证据的基本可信度函数组成的证据源bbm矩阵为M=[m1; m2]。对于两组证据的融合,表达式为
| $ {m_{{\rm{PCR}}}}\left( A \right) = m{_{12}}\left( A \right) + K\frac{{{c_{12}}\left( A \right)}}{{{e_{12}}}} $ | (8) |
| $ {m_{{\rm{PCR}}}}\left( \phi \right) = 0 $ | (9) |
式中:m12(A)=m1(A)·m2(A);c12(A)为矩阵M中对应焦元A所在列的非零列之和,即c12(A)=m1(A)+m2(A);e12为矩阵M中所有与冲突相关的非零列之和,在一般情况下有e12<2。
为反映证据权重给融合带来影响,对式(8) 进行改进。首先定义权值函数
| $ {w_{12}}\left( A \right) = {w_1}\left( A \right) + {w_2}\left( {A} \right) $ | (10) |
式中
相似度函数为
| $ \begin{array}{l} {d_{12}}\left( X \right) = 1 - \left[ {\max \left( {{m_i}\left( X \right)} \right) - {\rm{avg}}\left( {{m_i}\left( X \right)} \right)} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\left[ {\min \left( {{m_i}\left( X \right)} \right) - {\rm{avg}}\left( {{m_i}\left( X \right)} \right)} \right] \end{array} $ |
相似度函数反应两证据间对同一集合的支持程度,若两证据赋予同一集合的bba值越近,则相似度函数的值越大;反之,bba差别越大,则相似度函数的值越小。因此综合考虑证据的证据源矩阵、相似度函数及证据的权值,需要对整体冲突进行再分配,在仅有两个证据源的情况下,整体冲突对A的分配为
| $ \begin{array}{l} W{D_{12}}\left( A \right) = {w_{12}}\left( A \right){\rm{ }} \cdot {d_{12}}\left( A \right) \cdot \\ \;\;\;\;\;\left( {{m_{12}}\left( A \right) + {c_{12}}\left( A \right)} \right) \end{array} $ | (11) |
而整体分配中所有与A有关的整体冲突分配之和为
| $ {e_{12}} = \sum\limits_{\begin{array}{l} {A_i} \in {2^U} - \left\{ \phi \right\}\\ {B_i} \in {2^U} - \left\{ \phi \right\}\\ {A_i} \cap {B_i} = \phi \\ {m_{12}}\left( {{A_i} \cap {B_i}} \right) > 0 \end{array}} {{w_{12}}\left( A \right) \cdot {d_{12}}\left( A \right)\left( {{m_{12}}\left( A \right) + {c_{12}}\left( A \right)} \right)} $ |
则加权PCR融合法则的计算公式为
| $ {m_{{\rm{PCR}}}}\left( A \right) = \left\{ \begin{array}{l} {m_{12}}\left( A \right) + K\frac{{W{D_{12}}\left( A \right)}}{{{e_{12}}}}\;\;\;A{\rm{与冲突相关}}\\ {m_{12}}\left( A \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A{\rm{与冲突无关}} \end{array} \right. $ | (12) |
因传感器位置距离损伤位置的不确定性,故每组传感路径获得的损伤位置信息的可靠度不同。为反映某条传感路径两信号的差异,很多学者定义了不同的损伤指标,这些指标一般都是基于两信号能量的变化,其局限性在于:能量的计算是针对信号时域全局的能量,而信号的频散效应及边界的反射等因素的影响,会导致信号较为复杂,不能很好反映损伤对信号能量改变的贡献大小[20]。为减少边界反射等不良因素的影响,采用小波包分解的时频带能量的变化率作为传感路径的损伤指标,进而确定损伤路径信息的权值。
定义损伤指标为
| $ {R_i} = 1 - \frac{{\int_{{t_1}}^{{t_2}} {\int_{{\omega _1}}^{{\omega _2}} {{s_{i2}}\left( {\omega ,t} \right){\rm{d}}\omega {\rm{d}}t} } }}{{\int_{{t_1}}^{{t_2}} {\int_{{\omega _1}}^{{\omega _2}} {{s_{i1}}\left( {\omega ,t} \right){\rm{d}}\omega {\rm{d}}t} } }} $ | (13) |
式中:s2(ω, t)为检测信号;s1(ω, t)为健康基准信号;t1,t2为时宽的上下限;ω1,ω2为带宽的上下限。
对于式(13) 可采用小波包分解的方法具体实现。对信号进行N层小波包分解,可获得2N个正交频带,设小波包分解后第j层信号为Sj(t),则第j层频带的信号能量可以表示为
| $ {E_j} = \int {{S_j}\left( t \right)} {\rm{d}}t{\rm{ }} = \sum\limits_{l = 1}^L {{{\left| {K_j^l} \right|}^2}} {\rm{ }} $ | (14) |
式中Kjl为第j层信号中,第l个离散点的小波包分解系数。则t1到t2时间段内,第j层信号频带内的信号能量为
| $ {E_j} = \int_{{t_1}}^{{t_2}} {{S_j}\left( t \right)} {\rm{d}}t{\rm{ }} = \sum\limits_{l = {L_1}}^{{L_2}} {{{\left| {K_j^l} \right|}^2}} {\rm{ }} $ | (15) |
式中:L1为时间t1对应的离散点;L2为时间t2对应的离散点。
则式(13) 可表示为
| $ {R_i} = 1 - \frac{{\sum\limits_{l = {L_1}}^{{L_2}} {{{\left| {K_{i2j}^l} \right|}^2}} }}{{\sum\limits_{l = {L_1}}^{{L_2}} {{{\left| {K_{i1j}^l} \right|}^2}} }} $ | (16) |
将获得的多组Ri进行归一化处理,作为对应传感路径的权重值wi。
3.5 基于D-S证据理论的数据融合本文4个传感器分别作为激励与传感,可得到12组基准及检测信号。因此基于小波时频变换的方法,可获得12组时间延迟Δti。为获得更精确、鲁棒性更强的损伤定位图像,可针对图像中每一个像素点进行数据融合。具体融合的步骤如下:
(1) 根据结构健康状态下的基准信号和监测信号与基准信号之间的差信号进行小波变换,确定时间延迟Δti,并基于式(17) 计算板结构中离散点可能发生的概率
| $ {d_n} = \left\{ \begin{array}{l} 1 - \left| {\sqrt {{{\left( {{x_n} - {x_1}} \right)}^2} + {{\left( {{y_n} - {y_1}} \right)}^2}} - \sqrt {{{\left( {{x_n} - {x_2}} \right)}^2} + {\rm{ }}{{\left( {{y_n} - {y_2}} \right)}^2}} } - L\right| /L\;\;{d_n} > 0\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{d_n} \le 0 \end{array} \right. $ | (17) |
(2) 根据基准信号和差信号的小波包分解,确定特定时宽及带宽的能量变化率,确定传感路径的权重值wi;
(3) 建立辨识框架U=[有损伤,无损伤,不确定];
(4) 根据时间延迟Δti进行离散椭圆概率成像,以像素点的像素值作为该像素点对辨识框架的证据,该证据对与辨识框架内基本可信度按照式(18~20) 进行分配;
| $ m\left( {\left\{ {\rm{有损伤}} \right\}} \right) = \left\{ \begin{array}{l} {d_n}\;\;\;\;\;\;\;\;\;\;\;\;0.7 \le {d_n} \le 1\\ 2 \cdot {d_n} - 1\;\;\;0.3 \le {d_n} < 0.7\\ {d_n}/2\;\;\;\;\;\;\;\;0 \le {d_n} < 0.3 \end{array} \right. $ | (18) |
| $ m\left( {\left\{ {\rm{无损伤}} \right\}} \right) = \left\{ \begin{array}{l} \left( {1 - {d_n}} \right)/2\;\;\;\;0.7 \le {d_n} \le 1\\ 1 - {d_n}\;\;\;\;\;\;\;\;\;\;0.3 \le {d_n} < 0.7\\ 1 - {d_n}\;\;\;\;\;\;\;\;\;\;0 \le {d_n} < 0.3 \end{array} \right. $ | (19) |
| $ m\left( {\left\{ {\rm{不确定}} \right\}} \right) = \left\{ \begin{array}{l} \left( {1 - {d_n}} \right)/2\;\;\;\;0.7 \le {d_n} \le 1\\ 1 - {d_n}\;\;\;\;\;\;\;\;\;\;0.3 \le {d_n} < 0.7\\ {d_n}/2\;\;\;\;\;\;\;\;\;\;0 \le {d_n} < 0.3 \end{array} \right. $ | (20) |
(5) 遴选不相关的6条传感路径,按照式(12) 进行加权PCR证据融合;
(6) 根据{有损伤}的判定值进行成像,并进行阈值化处理,最终确定损伤位置。
根据上文所述的椭圆定位理论,为成像方便,将平板划分为若干像素点,每个像素点的坐标为(xn, yn),每组传感器的坐标分别为(x1, y1),(x2, y2)。根据小波变换时频分析确定的时间延迟Δt,可确定损伤可能出现的椭圆位置。则该像素点(xn, yn)到达两传感器最短距离,与该椭圆上的点到两传感器的距离之差,并经过归一化处理后,作为该像素点的像素值dn,表达式如式(17) 所示。
对于任意像素点建立辨识框架U={有损伤,无损伤,不确定},12条传感路径提供12组证据。根据式(17) 即可确定对应像素点上损伤出现的像素值dn,且有0≤dn≤1,该值可看作该像素点出现损伤的概率值。为合理分配证据对辨识框架中3个焦元的基本可信度,将dn划分为3个区域:[0.7 1],[0.3 0.7]和[0 0.3]。当dn处于[0.7 1]区间时,可以认为该点对{有损伤}的支持度较大,而对{无损伤}和{不确定}的支持度较小;当dn处于[0.3 0.7]区间时,可以认为该点对{不确定}的支持度较大,而对{无损伤}和{有损伤}的支持度较小;当dn处于[0 0.3]区间时,可以认为该点对{无损伤}的支持度较大,而对{有损伤}和{不确定}的支持度较小。具体按照式(18~20),确定基本可信度分配。采用加权PCR证据融合法则进行数据融合,以“有损伤”的最后结果,作为该像素点的像素值,进行成像处理,最终确定损伤位置。
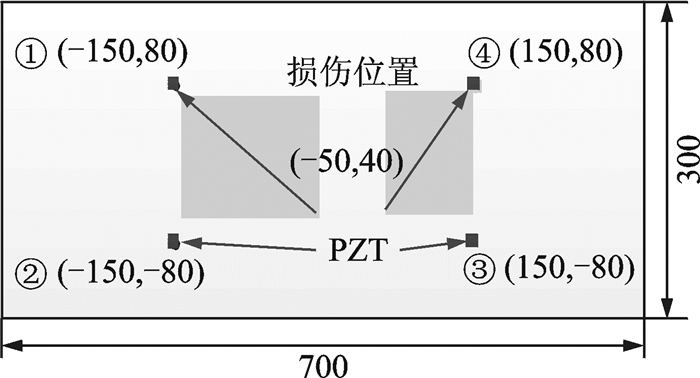
4 试验验证试验对象为700 mm×300 mm×3 mm的2A12铝合金薄板,图 4为试验件示意图,以板中心为(0, 0),分别在(-150,80), (150,80),(150,-80) 和(-150,-80) 位置处粘贴PZT传感器,4个传感器分别作为驱动器,其余3个作为传感器。采用NI数字采集设备和HSA 4052功率放大器进行驱动器的激发及传感器的信息采集,激励信号为汗宁窗调制的5周期正弦信号,其中心频率为250 kHz。采集频率为1 MHz。在板的(-50,40) 处设置直径为5 mm的通孔作为损伤状态,分别在健康及损伤状态下进行激励及采集,可分别获得12条路径的基准及检测信号,因传感路径存在重复,故可缩减为6条路径。
|
图 4 试验件示意图 Figure 4 Schematic of specimen |
分别采用连续小波变化及小波包分解的方法确定时间延迟及对应的权重值,如表 1所示。
| 表 1 传感路径的时间延迟及权重值 Table 1 Time delay and weight of different paths |
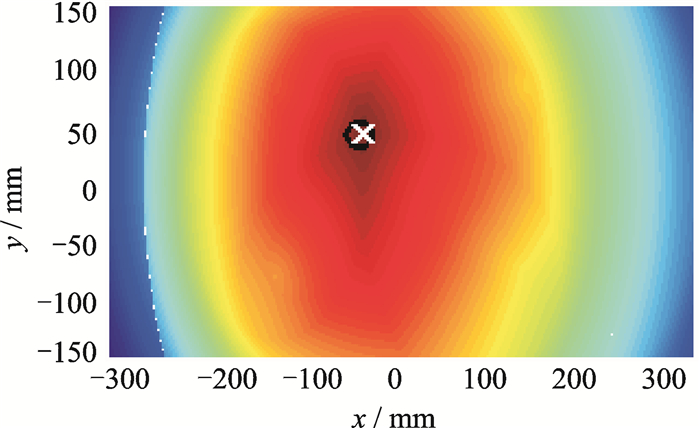
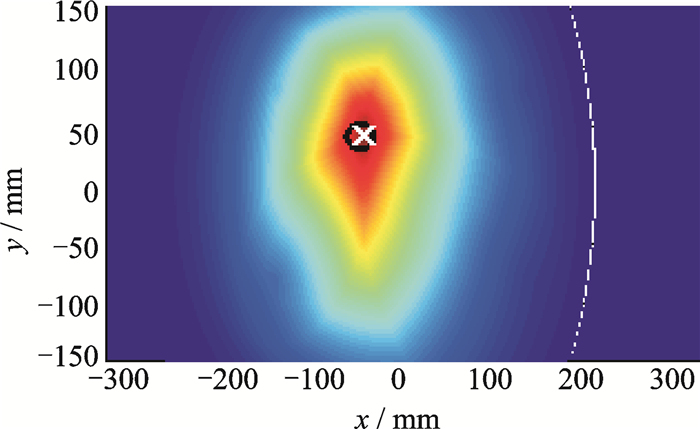
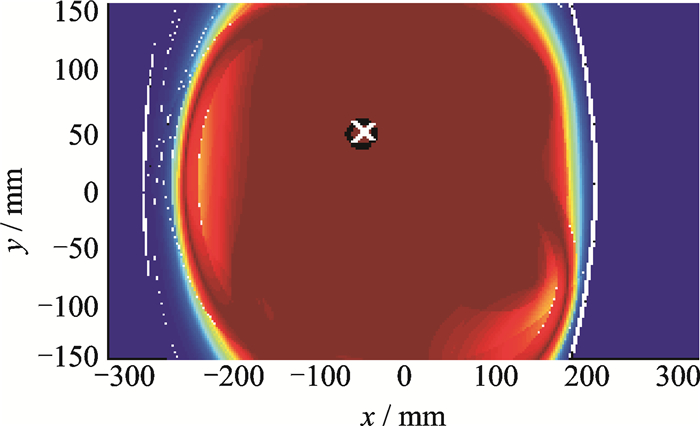
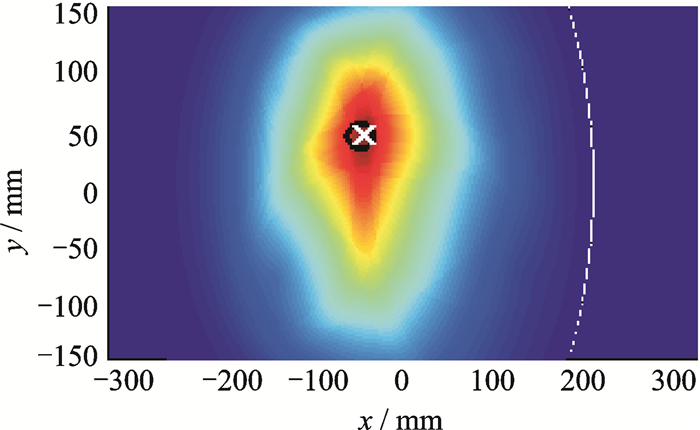
基于获得的时间延迟数据及测得的群速度,采用椭圆定位法进行成像,并分别采用全加算法、全乘算法、原始D-S证据融合算法和改进的加权PCR证据融合算法对6条传感路径进行融合,融合结果分别如图 5~8所示,其中“×”代表像素值最大点位置,即为最可能出现损伤的位置,其具体坐标为括号内坐标数据,“○”代表实际损伤位置。
|
图 5 全加算法(-46.5,41) Figure 5 Full summation method (-46.5, 41) |
|
图 6 全乘算法(-46.5,41) Figure 6 Full multiplication method(-46.5, 41) |
|
图 7 D-S证据融合算法(-47,41) Figure 7 D-S evidence fusion method (-47, 41) |
|
图 8 加权PCR证据融合算法(-47.5,41) Figure 8 Weighted PCR evidence fusion method(-47.5, 41) |
从图中可以看出,全乘算法及加权PCR算法的定位成像对比度效果较好,全加算法成像质量一般,而原始DS证据理论的定位成像效果较差,其成像较差的原因是各条路径提供的证据存在一定的冲突。通过阈值化处理,取其像素值最大点,作为损伤位置,4种融合算法的定位结果分别为:(-46.5,41), (-46.5,41), (-47,41), (-47.5,41),与损伤的准确位置(-50,40) 存在一定的偏差,这是由于损伤及传感器并不是一个质点,而是一个面元所引起的。因定位结果较为一致,说明了本文所提的加权PCR证据融合算法的适用性,且成像分辨率较好。
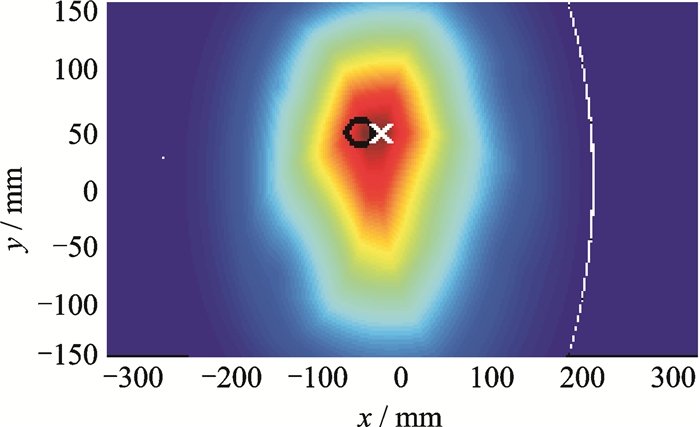
为验证本文所提方法在可靠性方面的优势,将差信号能量较小的传感路径3-4所确定的时间延迟由5.576×10-5 s进行调整为4.576×10-5 s,其他路径保持不变。为观察加权因子对全加和全乘法的影响,分别对全加及全乘算法进行加权处理。得到不加权的全加及全乘算法、加权的全加及全乘算法和加权PCR融合算法的结果如图 9~13所示,定位误差分析见表 2。
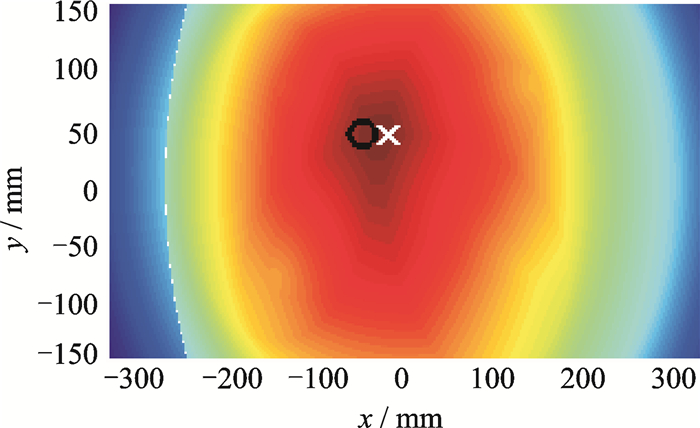
|
图 9 未加权的全加算法成像(-20,39.5) Figure 9 Unweighted full summation method(-20, 39.5) |
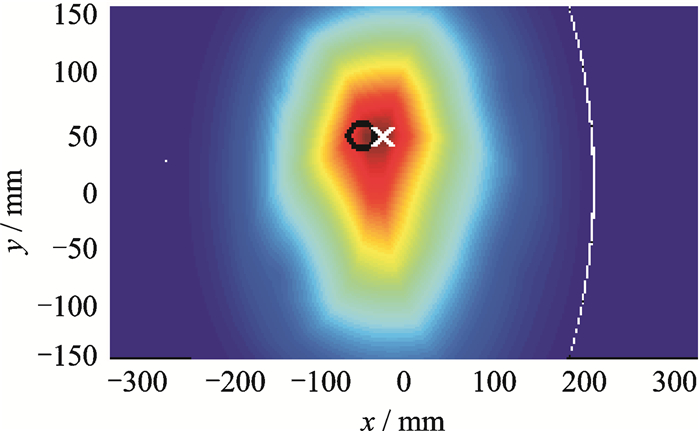
|
图 10 未加权的全乘算法成像(-25,39) Figure 10 Unweighted full multiplication method(-25, 39) |
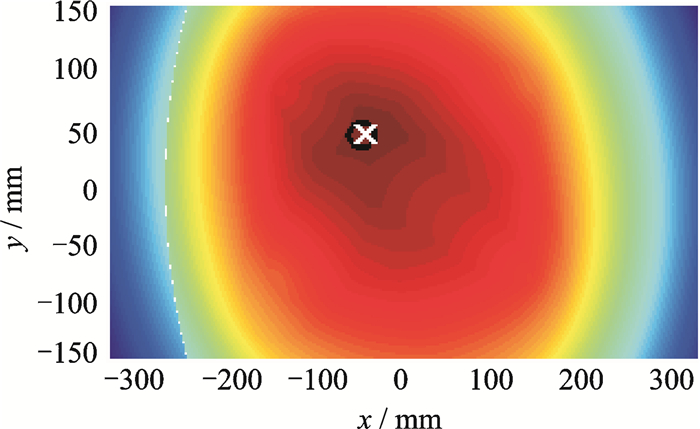
|
图 11 加权的全加算法成像(-46.5,41) Figure 11 Weighted full summation method(-46.5, 41) |
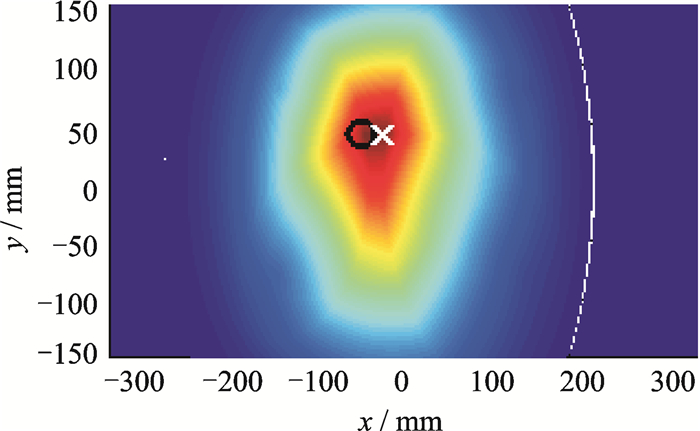
|
图 12 加权的全乘算法(-25 39) Figure 12 Weighted full multiplication method(-25 39) |
|
图 13 加权PCR证据融合算法成像(-34.5 38.5) Figure 13 Weighted PCR evidence fusion method(-34.5 38.5) |
| 表 2 定位结果分析 Table 2 Analysis of localization r esults |
上述成像结果表明,不加权的全加和全乘成像算法及加权的全乘算法均因部分路径时间延迟判断失准而造成定位误差增大。而加权的全加成像算法,在阈值化处理后,取其像素值最大点,作为损伤位置,其坐标仍为(46,41.5),但从成像效果看,成像对比度下降较大。加权PCR证据融合算法的成像结果显示,损伤定位也因部分路径时间延迟判定失准而定位误差增大,但整体误差增大的程度相较前几种成像方法较小,同时损伤成像的对比度也较好。因此,证明基于加权PCR证据融合算法的成像方法在应对部分传感路径定位失准情况具有较大的优势。
5 结束语本文针对目前在基于Lamb波的多传感器损伤定位成像中,全加法成像对比度不高、全乘法成像可靠性相对较差的问题,提出了一种基于加权的PCR证据融合的损伤成像方法。通过对基准信号与差信号进行小波变换,确定了路径的时间延迟;介绍了PCR融合法则,以解决冲突证据的融合问题;以信号小波包分解为手段,提出了一种以路径信号频带局部能量变化作为路径信息权重的方法;提出了一种基于加权PCR证据融合的多传感器损伤成像方法。试验结果证明,在成像对比度方面,该方法与全乘法相近,而强于全加法;在应对部分路径时间延迟判断失准的能力方面,该方法强于全加法、全乘法及加权全乘法,而略低于加权全加法。试验说明,本文所提方法可以应用于多传感路径的定位图像融合中,以提高应对人为或自然引起的部分传感路径定位失准的能力,提高损伤定位的可靠性。
| [1] |
袁慎芳.
结构健康监控[M]. 北京: 国防工业出版社, 2007.
YUAN Shenfang. Structural health monitoring and damage control[M]. Beijing: National Defense Industry Press, 2007. |
| [2] | KIJANKA P, MANOHAR A, di SCALEA F L, et al. Damage location by ultrasonic Lamb waves and piezoelectric rosettes[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(12): 1477–1490. DOI:10.1177/1045389X14544140 |
| [3] |
孙侠生, 肖迎春.
飞机结构健康监测技术的机遇与挑战[J]. 航空学报, 2014, 35(12): 3199–3212.
SUN Xiasheng, XIAO Yingchun. Opportunities and challenges of aircraft structural health monitoring[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3199–3212. |
| [4] | SU Z, YE L, LU Y. Guided lamb waves for identification of damage in composite structures: A review[J]. Journal of Sound & Vibration, 2006, 295(3/4/5): 753–780. |
| [5] | RAGHAVAN A, CESNIK C E S. Review of guided-wave structural health monitoring[J]. Shock & Vibration Digest, 2007, 39(2): 91–114. |
| [6] |
严刚, 周丽, 孟伟杰.
基于Lamb波与时频分析的复合材料结构损伤监测和识别[J]. 南京航空航天大学学报, 2007, 39(3): 397–402.
YAN Gang, ZHOU Li, MENG Weijie. Damage detection and identification for composites based on lamb waves and time-frequency analysis method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(3): 397–402. |
| [7] |
严刚, 周丽.
基于频率-波数域偏移方法的板结构损伤实时识别[J]. 振动工程学报, 2008, 21(6): 620–625.
YAN Gang, ZHOU Li. Real time identification of damages for plate-like structure using migration technique in frequency-wavenumber domain[J]. Journal of Vibration Engineering, 2008, 21(6): 620–625. |
| [8] |
张望, 吴维亮, 肖黎, 等.
闭合型裂纹时间反转损伤识别[J]. 振动与冲击, 2015(9): 95–101.
ZHANG Wang, WU Weiliang, XIAO Li, et al. Time reversal based damage detection for closed crack[J]. Journal of Vibration and Shock, 2015(9): 95–101. |
| [9] |
孙亚杰, 高艺, 薛瑶环, 等.
相控阵超声监测成像与直方图匹配图像增强实验研究[J]. 传感技术学报, 2015(1): 86–92.
SUN Yajie, GAO Yi, XUE Yaohuan, et al. Experimental research on phased array ultrasonic monitoring imaging and histogram matching based image enhancement[J]. Chinese Journal of Sensors and Actuators, 2015(1): 86–92. |
| [10] | GANGADHARAN R, MURTHY C R L, GOPALAKRISHNAN S, et al. Time reversal technique for health monitoring of metallic structure using lamb waves[J]. Ultrasonics, 2009, 49(8): 696–705. DOI:10.1016/j.ultras.2009.05.002 |
| [11] | CHEN X, MICHAELS J E, LEE S J, et al. Load-differential imaging for detection and localization of fatigue cracks using Lamb waves[J]. NDT & E International, 2012, 51: 142–149. |
| [12] |
刘增华, 樊军伟, 何存富, 等.
基于概率损伤算法的复合材料板空气耦合Lamb波扫描成像[J]. 复合材料学报, 2015, 32(1): 227–235.
LIU Zenghua, FAN Junwei, HE Cunfu, et al. Scanning imaging of composite plate using air-coupled lamb waves based on probabilistic damage algorithm[J]. Acta Materiae Compositae Sinica, 2015, 32(1): 227–235. |
| [13] |
徐庆龙. 基于时间反转Lamb波的典型结构检测技术研究[D]. 北京: 北京工业大学, 2014.
XU Qinglong. Research on typical structure detection technology based on time-reversal lamb waves [D]. Beijing: Beijing University of Technology, 2014.http: //cdmd. cnki. com. cn/article/cdmd-10005-1015006592. htm |
| [14] |
刘丽娟. 基于DS证据理论的多传感器信息融合算法研究—在移动机器人地图创建中的应用[D]. 无锡: 江南大学, 2014.
LIU Lijuan. Algorithm research on multi-sensor information fusion based on D-S evidence theory: Application in mobile robot map building[D].Wuxi: Jiangnan University, 2014.http: //cdmd. cnki. com. cn/Article/CDMD-10295-1014380460. htm |
| [15] |
刘志成, 乔慧, 何佳洲.
基于加权证据距离的高度冲突证据组合方法[J]. 计算机工程与应用, 2014, 50(3): 103–107.
LIU Zhicheng, QIAO Hui, HE Jiazhou. Combination approach of highly conflict evidence based on weighted distance of evidence[J]. Computer Engineering and Applications, 2014, 50(3): 103–107. |
| [16] |
熊彦铭, 杨战平, 屈新芬.
基于模型修正的冲突证据组合新方法[J]. 控制与决策, 2011, 26(6): 883–887.
XIONG Yanming, YANG Zhanping, QU Xinfen. Novel combination method of conflict evidence based on evidential model modification[J]. Control and Decision, 2011, 26(6): 883–887. |
| [17] |
梁威, 魏宏飞, 周锋.
DS证据理论中一种冲突证据的融合方法[J]. 计算机工程与应用, 2011, 47(6): 144–146.
LIANG Wei, WEI Hongfei, ZHOU Feng. Fusion method of conflict evidence in D-S theory[J]. Computer Engineering and Applications, 2011, 47(6): 144–146. |
| [18] | SCHUBERT J. Conflict management in Dempster-Shafer theory using the degree of falsity[J]. International Journal of Approximate Reasoning, 2011, 52(3): 449–460. DOI:10.1016/j.ijar.2010.10.004 |
| [19] |
王进花, 吴迪, 曹洁, 等.
基于证据分类的加权冲突证据组合[J]. 计算机科学, 2013, 40(1): 247–250.
WANG Jinhua, WU Di, CAO Jie, et al. Weighted combination of conflicting evidence based on evidence classification[J]. Computer Science, 2013, 40(1): 247–250. |
| [20] |
邹兆年. 加权证据组合算法的研究[D]. 长春: 吉林大学, 2005.
ZOU Zhaonian, The research of combination algorithm of weighted evidence[D]. Changchun: Jilin University, 2005.http: //cdmd. cnki. com. cn/Article/CDMD-10183-2005105883. htm |
| [21] |
王奉涛, 马孝江, 邹岩崑, 等.
基于小波包分解的频带局部能量特征提取方法[J]. 农业机械学报, 2004, 35(5): 177–180.
WANG Fengtao, MA Xiaojiang, ZOU Yankun, et al. Local power feature extraction method of frequency bands based on wavelet packet decomposition[J]. Transactions of the Chinese Society of Agricultural Machinery, 2004, 35(5): 177–180. |
 2017, Vol. 49
2017, Vol. 49


