随着信息时代的飞速发展，无线通信已经融入到人类社会的各个方面，一方面，由于电子商务、社交网络、公共安全等对无线服务的需求持续升高，导致可用的无线频谱资源十分紧张，因此认知无线电技术得到了广泛的关注。另一方面，由于无线传输媒介的开放性、信息传输的无界性、无线网络的互动性等特点，无线通信在给人们生活带来极大便利的同时，也使得用户的个人信息、个人隐私、财产安全受到了严重威胁。鉴于认知无线网络中主、次网络间存在的相互干扰，人们利用多天线技术引入了预编码、集中式或分布式波束赋形、协同人工干扰等信号处理方法，用于增强认知无线网络的物理层安全性能。文献[1]以认知网络安全速率为目标，设计了主网络干扰温度约束下多天线认知网络的最优和次优波束赋形方案。文献[2]将人工干扰应用于认知无线传感器网络，以改善网络的安全中断性能。进而，文献[3]考虑配置多中继的两跳协同认知网络，研究了主、次网络之间的相互干扰对安全速率的影响，并通过设计中继处不同的分布式波束赋形向量来增强物理层安全性能。

面向下一代移动应用的认知蜂窝网络中有复杂的网络结构、众多的网络节点，大大扩展了信号处理的可用维度，为通过信号处理增强物理层安全性能提供了可能。文献[4]中设计了一种联合协同人工干扰和波束赋形的混合预编码传输方案，可明显改善协同无线网络的物理层安全性能。类似地，在认知蜂窝网络中进行联合信号处理，充分发挥各种信号处理方法的优势亦是改善物理层安全性能的有效途径之一。值得一提的是，干扰对准技术可将多个发送信号在多个信号维度上进行编码传输，通过联合设计收发信机可以在任意接收端将干扰信号对准到某个低维度的信号子空间中，从而实现有用信号在其他信号子空间中无干扰传输^[5]，这为增强物理层安全性能的联合信号处理提供参考。文献[6]将干扰对准思想应用于协同无线网络中，通过合法用户的发送预编码矩阵、接收滤波矩阵设计将协同人工干扰信号对准窃听节点，且在合法接收端实现无干扰传输，提高了系统的安全性能。上述的研究工作主要是在信道信息精确已知下进行的，在非理想条件下的认知蜂窝网络中如何借鉴干扰对准思想，高效地管理和利用主、次网络之间的相互干扰及协同人工干扰，设计优化的预编码或波束赋形方案来增强物理层安全性能值得深入研究。

本文在非理想的认知蜂窝系统中借鉴干扰对准思想，高效地管理和利用主、次网络之间的相互干扰，通过迭代求解优化设计发送预编码矩阵和接收滤波矩阵，在避免干扰合法用户接收的同时尽可能对窃听节点实施阻塞干扰。通过理论分析和Monte Carlo仿真发现：基于干扰对准设计预编码矩阵的系统性能明显优于随机预编码设计的系统性能，但随着信道非精确程度的增大，干扰对准方案相较于随机预编码设计的性能下降严重，揭示了信道估计精度对系统设计的重要意义。

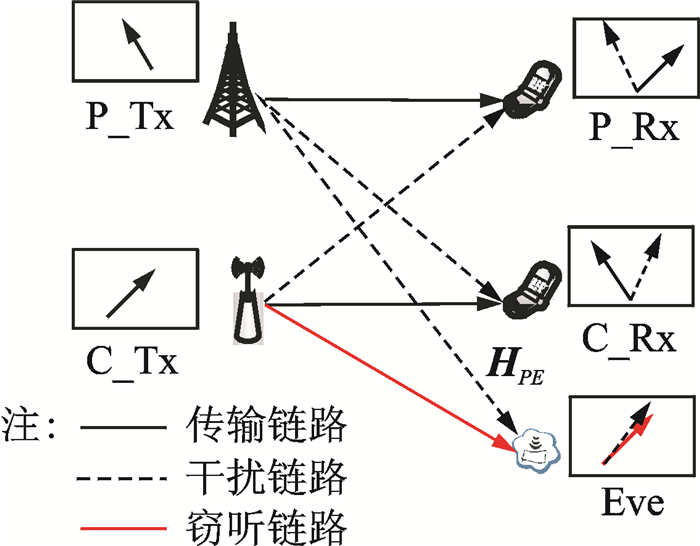
1 系统模型 1.1 干扰对准模型

本文分析的认知网络无线下的系统模型如图 1所示，其次用户系统有一个发送者C_Tx，一个接收者C_Rx，主用户系统由一个发送者P_Tx和一个接收者P_Rx组成。主用户发送端和接收端分别配备M_P和N_P根天线，次用户发送端和接收端分别配备M_C和N_C根天线，同时考虑存在窃听节点(Eve)窃听次网络的传输信息。

假定主网络中发送预编码矩阵为U_P，接收滤波矩阵为V_P，次网络中发送预编码矩阵为U_C，接收滤波矩阵为V_C。如果直接借鉴干扰对准思想，可通过设计主、次网络中的发送预编码矩阵和接收滤波矩阵，使主、次网络发送信号在对应的接收信号空间上相互分离，以保障无干扰传输，同时使主网络发送的信号对于窃听节点实施最大化干扰，即使得次网络信号和主网络信号在窃听节点的接收信号空间混叠。这就要求主、次网络中发送预编码矩阵和接收滤波矩阵满足以下条件

$\left\{ \begin{array}{l} {\boldsymbol{V}_C}{\boldsymbol{H}_{CP}}{\boldsymbol{U}_P} = 0\\ {\boldsymbol{V}_P}{\boldsymbol{H}_{PC}}{\boldsymbol{U}_C} = 0\\ {\boldsymbol{H}_{EP}}{\boldsymbol{U}_P} = {\boldsymbol{H}_{EC}}{\boldsymbol{U}_C} \end{array} \right.$

(1)

式中：H_CP为主网络发送端到次网络接收端的信道矩阵；H_PC为次网络发送端到主网络接收端的信道矩阵；H_EP为主网络发送端到窃听节点的信道矩阵；H_EC为次网络发送端到窃听节点的信道矩阵。

1.2 信道误差模型

类似于文献[7, 8]的假设，在分布式的过程中假定发送预编码矩阵和接收滤波矩阵都受限于非精确的信道状态信息，本文所分析时考虑的信道非理想条件主要是由于“反馈时延”的影响，研究分析中发送端通常需要获知信道估计的链路信息以便进行有用数据的信号处理，然而由于无线信道的时变性和信道估计、反馈等处理过程，该信道状态信息与实际发送数据符号时所经历的信道不可避免的存在时延，假设为T_d。普通的方法是通过高斯马尔科夫过程表征${{\boldsymbol{\tilde H}}_{ab}}$与H_ab间的数学关系

${{\boldsymbol{\tilde H}}_{ab}} = \rho {\boldsymbol{H}_{ab}} + {\boldsymbol{E}_{ab}}$

(2)

式中：$\rho = E\left[{\mathit{\boldsymbol{\tilde H}}_{ab}^\mathit{\dagger }{\mathit{\boldsymbol{H}}_{ab}}} \right]/E\left[{\mathit{\boldsymbol{H}}_{ab}^\mathit{\dagger }{\mathit{\boldsymbol{H}}_{ab}}} \right]$表示时延相关函数，由文献[9]可知，Clarke信道模型下有ρ=J₀2πf_dT_d，其中J₀(·)表示文献[10]中的第一类零阶贝塞尔函数，f_d为最大多普勒频移，T_d为信道时延。同时假定时延误差复高斯矩阵E_ab与信道矩阵H_ab相互独立, 其由均值为零，方差为1-ρ²的元素组成，即

${\rm{vec}}\left( {{\mathit{\boldsymbol{E}}_{ab}}} \right) \sim {N_C}\left( {{\bf{0}}, \left( {1-{\rho ^2}} \right)\mathit{\boldsymbol{I}}} \right)$

(3)

式中：vec (·)表示对矩阵的向量化。

2 干扰对准方案

基于文献[11]干扰对准的思想，认知蜂窝网络中主次用户干扰对准后次网络的安全传输速率可以表示为

$\begin{array}{c} {R_S} = \log \left| {{\mathit{\boldsymbol{I}}_{{d_C}}} + {\mathit{\boldsymbol{V}}_C}{\mathit{\boldsymbol{H}}_{CC}}{\mathit{\boldsymbol{U}}_C}\mathit{\boldsymbol{U}}_C^\dagger \mathit{\boldsymbol{H}}_{CC}^\dagger \mathit{\boldsymbol{V}}_C^\dagger \frac{{{P_C}}}{{{d_c}}}} \right|-\\ \log \left| {{\mathit{\boldsymbol{I}}_{{d_E}}} + \frac{{{\mathit{\boldsymbol{V}}_E}{\mathit{\boldsymbol{H}}_{EC}}{\mathit{\boldsymbol{U}}_C}\mathit{\boldsymbol{U}}_C^\dagger \mathit{\boldsymbol{H}}_{EC}^\dagger \mathit{\boldsymbol{V}}_E^\dagger }}{{{\mathit{\boldsymbol{V}}_E}{\mathit{\boldsymbol{H}}_{EP}}{\mathit{\boldsymbol{U}}_P}\mathit{\boldsymbol{U}}_P^\dagger \mathit{\boldsymbol{H}}_{EP}^\dagger \mathit{\boldsymbol{V}}_E^\dagger \left( {{P_P}/{d_P}} \right) + {\mathit{\boldsymbol{I}}_{E{N_O}}}}}\frac{{{P_C}}}{{{d_C}}}} \right| \end{array} $

(4)

式中：H_CC为次网络发送端到次网络接收端的信道矩阵；P_P为主网络发送功率；P_C为次网络发送功率；d_C和d_E分别为次网络和窃听链路的传输自由度，其分别满足d_C=rank{V_CH_CCU_C}≥1和d_E=rank{V_EH_ECU_C}≥1；I_ENO为窃听节点处噪声功率的d_E×d_E维单位对角阵。

本文发送预编码矩阵和接收滤波矩阵的迭代求解是基于过时的非精确的信道状态信息。求得的发送接收预编码矩阵是非精确的，分别用${\boldsymbol{\tilde U}_C}, {\boldsymbol{\tilde U}_P}, {\boldsymbol{\tilde V}_P}和{\boldsymbol{\tilde V}_C}$表示。另外，本文对式(4)中的策略进行了改进，即主、次用户间的相互干扰没有必要完全对准到各自的零空间。事实上，针对频谱共享的认知蜂窝网络，对主网络来说只要满足给定的干扰温度约束Γ即可。此时，基于非理想信道信息的最大化次网络安全传输速率的发送预编码矩阵和接收滤波矩阵对应于如下优化问题的解

$\begin{array}{c} {R_S} = \mathop {\arg \max }\limits_{{\mathit{\boldsymbol{U}}_P}, {\mathit{\boldsymbol{U}}_C}, {\mathit{\boldsymbol{V}}_P}, {\mathit{\boldsymbol{V}}_C}, {\mathit{\boldsymbol{V}}_E}} \log \left| {{\mathit{\boldsymbol{I}}_{{d_C}}} + {\rm{SIN}}{{\rm{R}}_C}} \right|-\\ \log \left| {{\mathit{\boldsymbol{I}}_{{d_E}}} + {\rm{SIN}}{{\rm{R}}_E}} \right|\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{\rm{SIN}}{{\rm{R}}_P} \le \mathit{\Gamma } \end{array}$

(5)

式中:${\rm{SNIR = }}\frac{{{{\mathit{\boldsymbol{\tilde V}}}_P}{\mathit{\boldsymbol{H}}_{PP}}{{\mathit{\boldsymbol{\tilde U}}}_P}\mathit{\boldsymbol{\tilde U}}_P^\mathit{\dagger}\mathit{\boldsymbol{H}}_{PP}^\mathit{\dagger}\mathit{\boldsymbol{\tilde V}}_P^\mathit{\dagger}}}{{{{\mathit{\boldsymbol{\tilde V}}}_P}{\mathit{\boldsymbol{H}}_{PC}}{{\mathit{\boldsymbol{\tilde U}}}_C}\mathit{\boldsymbol{\tilde U}}_C^\mathit{\dagger}\mathit{\boldsymbol{H}}_{PC}^\mathit{\dagger}\mathit{\boldsymbol{\tilde V}}_P^\mathit{\dagger}\left( {{P_C}/{d_C}} \right) + {\mathit{\boldsymbol{I}}_{P{N_P}}}}} \cdot \frac{{{P_P}}}{{{d_P}}}$，${\rm{SNIR = }}\frac{{{{\mathit{\boldsymbol{\tilde V}}}_C}{\mathit{\boldsymbol{H}}_{CC}}{{\mathit{\boldsymbol{\tilde U}}}_C}\mathit{\boldsymbol{\tilde U}}_C^\mathit{\dagger}\mathit{\boldsymbol{H}}_{CC}^\mathit{\dagger}\mathit{\boldsymbol{\tilde V}}_C^\mathit{\dagger}}}{{{{\mathit{\boldsymbol{\tilde V}}}_P}{\mathit{\boldsymbol{H}}_{CP}}{{\mathit{\boldsymbol{\tilde U}}}_P}\mathit{\boldsymbol{\tilde U}}_P^\mathit{\dagger}\mathit{\boldsymbol{H}}_{CP}^\mathit{\dagger}\mathit{\boldsymbol{\tilde V}}_C^\mathit{\dagger}\left( {{C_P}/{d_P}} \right) + {\mathit{\boldsymbol{I}}_{C{N_C}}}}} \cdot \frac{{{C_C}}}{{{d_C}}}$和${\rm{SNIR = }}\frac{{{{\mathit{\boldsymbol{\tilde V}}}_E}{\mathit{\boldsymbol{H}}_{EE}}{{\mathit{\boldsymbol{\tilde U}}}_E}\mathit{\boldsymbol{\tilde U}}_E^\mathit{\dagger}\mathit{\boldsymbol{H}}_{EE}^\mathit{\dagger}\mathit{\boldsymbol{\tilde V}}_E^\mathit{\dagger}}}{{{{\mathit{\boldsymbol{\tilde V}}}_E}{\mathit{\boldsymbol{H}}_{EC}}{{\mathit{\boldsymbol{\tilde U}}}_C}\mathit{\boldsymbol{\tilde U}}_C^\mathit{\dagger}\mathit{\boldsymbol{H}}_{EC}^\mathit{\dagger}\mathit{\boldsymbol{\tilde V}}_E^\mathit{\dagger}\left( {{E_C}/{d_C}} \right) + {\mathit{\boldsymbol{I}}_{E{N_E}}}}} \cdot \frac{{{E_E}}}{{{d_E}}}$分别表示经过干扰对准后主、次网络接收端和窃听节点接收端的信干噪比，H_PP为主网络发送端到主网络接收端的信道矩阵，d_P为主网络的传输自由度，其满足d_P=rank{V_PH_PPU_P}≥1，I_PNO和I_CNO分别为主用户接收端和次用户接收端噪声功率的d_P×d_P维和d_C×d_C维单位对角阵。

为了求解式(5)中的问题，先通过优化预编码矩阵${{\mathit{\boldsymbol{\tilde U}}}_C}, {{\mathit{\boldsymbol{\tilde U}}}_P}和{{\mathit{\boldsymbol{\tilde V}}}_C}$使式(5)中第一项达到最大，依据文献[11]中的分布式迭代方案，设计本文的迭代方案如下：

步骤1  初始化主用户和次用户发送端预编码矩阵_PC，所取预编码矩阵要满足

$\mathit{\boldsymbol{\tilde U}}_P^\mathit{\dagger }{{\mathit{\boldsymbol{\tilde U}}}_P} = {\mathit{\boldsymbol{I}}_{{d_P}}}, \mathit{\boldsymbol{\tilde U}}_C^\mathit{\dagger }{{\mathit{\boldsymbol{\tilde U}}}_C} = {\mathit{\boldsymbol{I}}_{{d_C}}}$

步骤2  分别计算主用户接收端和次用户接收端的干扰和噪声协方差矩阵为

$\begin{array}{l} {{\boldsymbol{\tilde B}}_P} = {{\boldsymbol{\tilde H}}_{PC}}{{\boldsymbol{\tilde U}}_C}\boldsymbol{\tilde U}_C^\mathit{\dagger}\boldsymbol{\tilde H}_C^\mathit{\dagger}\left( {{P_P}/{d_P}} \right) + {\boldsymbol{I}_{P{N_O}}}\\ {{\boldsymbol{\tilde B}}_C} = {{\boldsymbol{\tilde H}}_{CP}}{{\boldsymbol{\tilde U}}_P}\boldsymbol{\tilde U}_P^\mathit{\dagger}\boldsymbol{\tilde H}_{CP}^\mathit{\dagger}\left( {{P_C}/{d_C}} \right) + {\boldsymbol{I}_{C{N_O}}} \end{array}$

步骤3  主用户和次用户接收端的接收滤波矩阵分别表示为

${{\boldsymbol{\tilde V}}_P} = \frac{{{{\left( {{{\boldsymbol{\tilde B}}_C}} \right)}^{-1}}{{\boldsymbol{\tilde H}}_{PP}}{{\boldsymbol{\tilde U}}_P}}}{{\left\| {{{\left( {{{\boldsymbol{\tilde B}}_C}} \right)}^{-1}}{{\boldsymbol{\tilde H}}_{PP}}{{\boldsymbol{\tilde U}}_P}} \right\|}}\;\;{{\boldsymbol{\tilde V}}_P} = \frac{{{{\left( {{{\boldsymbol{\tilde B}}_P}} \right)}^{-1}}{{\boldsymbol{\tilde H}}_{CC}}{{\boldsymbol{\tilde U}}_C}}}{{\left\| {{{\left( {{{\boldsymbol{\tilde B}}_P}} \right)}^{ - 1}}{{\boldsymbol{\tilde H}}_{CC}}{{\boldsymbol{\tilde U}}_C}} \right\|}}$

步骤4  信道的互易性，互换上下行方向，且令

${\widehat {\mathit{\boldsymbol{\tilde U}}}_C} = {{\mathit{\boldsymbol{\tilde V}}}_C}\;\;{\widehat {\mathit{\boldsymbol{\tilde U}}}_P} = {{\mathit{\boldsymbol{\tilde V}}}_P}$

步骤5  计算互易网络中的干扰和噪声协方差矩阵

$\begin{array}{l} {\widehat {\mathit{\boldsymbol{\tilde B}}}_C} = {\widehat {\mathit{\boldsymbol{\tilde H}}}_{CP}}{\widehat {\mathit{\boldsymbol{\tilde U}}}_C}\widehat {\mathit{\boldsymbol{\tilde U}}}_C^\dagger\widehat {\mathit{\boldsymbol{\tilde H}}}_{CP}^\dagger\left( {{P_C}/{d_C}} \right) + {{\mathit{\boldsymbol{\hat I}}}_{C{N_O}}}\\ {\widehat {\mathit{\boldsymbol{\tilde B}}}_P} = {\widehat {\mathit{\boldsymbol{\tilde H}}}_{PC}}{\widehat {\mathit{\boldsymbol{\tilde U}}}_P}\widehat {\mathit{\boldsymbol{\tilde U}}}_{PC}^\dagger\widehat {\mathit{\boldsymbol{\tilde H}}}_{PC}^\dagger\left( {{P_C}/{d_C}} \right) + {{\mathit{\boldsymbol{\hat I}}}_{P{N_O}}} \end{array}$

步骤6  计算其接收滤波矩阵

${\widehat {\mathit{\boldsymbol{\tilde V}}}_P} = \frac{{{{\left( {{{\widehat {\mathit{\boldsymbol{\tilde B}}}}_C}} \right)}^{-1}}{{\widehat {\mathit{\boldsymbol{\tilde H}}}}_{PP}}{{\widehat {\mathit{\boldsymbol{\tilde U}}}}_P}}}{{\left\| {{{\left( {{{\widehat {\mathit{\boldsymbol{\tilde B}}}}_C}} \right)}^{-1}}{{\widehat {\mathit{\boldsymbol{\tilde H}}}}_{PP}}{{\widehat {\mathit{\boldsymbol{\tilde U}}}}_P}} \right\|}}\;\;\;\;{\widehat {\mathit{\boldsymbol{\tilde V}}}_P} = \frac{{{{\left( {{{\widehat {\mathit{\boldsymbol{\tilde B}}}}_C}} \right)}^{-1}}{{\widehat {\mathit{\boldsymbol{\tilde H}}}}_{PP}}{{\widehat {\mathit{\boldsymbol{\tilde U}}}}_P}}}{{\left\| {{{\left( {{{\widehat {\mathit{\boldsymbol{\tilde B}}}}_C}} \right)}^{ - 1}}{{\widehat {\mathit{\boldsymbol{\tilde H}}}}_{PP}}{{\widehat {\mathit{\boldsymbol{\tilde U}}}}_P}} \right\|}}$

步骤7  互换上下行方向，且设

${{\mathit{\boldsymbol{\tilde U}}}_C} = {\widehat {\mathit{\boldsymbol{\tilde V}}}_C}\;\;{{\mathit{\boldsymbol{\tilde U}}}_P}{\widehat {\mathit{\boldsymbol{\tilde V}}}_P}$

步骤8  重复步骤2~7，直至收敛或达到预先设定的最大迭代步数为止。

基于上述算法计算出了最优的发送和接收预编码矩阵${{\mathit{\boldsymbol{\tilde U}}}_C}, {{\mathit{\boldsymbol{\tilde V}}}_C}和{{\mathit{\boldsymbol{\tilde U}}}_P}, {{\mathit{\boldsymbol{\tilde V}}}_P}$，现在需要求窃听端的窃听矩阵${{\mathit{\boldsymbol{\tilde V}}}_E}$，根据窃听端的目的，窃听端的接收矩阵就要使窃听到的信息最大化

${{\mathit{\boldsymbol{\tilde V}}}_E} = \max {\rm{ei}}{{\rm{g}}_{{\rm{unit}}}}\left( {{\mathit{\boldsymbol{B}}^{-1}}\mathit{\boldsymbol{A}}} \right)$

(6)

式中：$\boldsymbol{B} = {{\boldsymbol{\tilde H}}_{EP}}{{\boldsymbol{\tilde U}}_P}\boldsymbol{\tilde U}_P^\dagger\boldsymbol{\tilde H}_{EP}^\dagger\left( {{P_P}/{d_P}} \right) + {\boldsymbol{I}_{E{N_O}}}$，$\boldsymbol{A} = {{\boldsymbol{\tilde H}}_{EC}}{{\boldsymbol{\tilde U}}_C}\boldsymbol{\tilde U}_C^\dagger\boldsymbol{\tilde H}_{EC}^\dagger$，其中${{\boldsymbol{\tilde V}}_E}$取B^-1A最大的d_E个特征值对应的特征向量。

基于用户可达速率的定义^{[7, 12]}，干扰对准后次用户的安全速率表示为

$\begin{array}{l} \log \left| {{\mathit{\boldsymbol{I}}_{{d_C}}} + \frac{{{{\mathit{\boldsymbol{\tilde V}}}_C}{\mathit{\boldsymbol{H}}_{CC}}{{\mathit{\boldsymbol{\tilde U}}}_C}\mathit{\boldsymbol{\tilde U}}_C^\dagger\mathit{\boldsymbol{H}}_{CC}^\dagger\mathit{\boldsymbol{\tilde V}}_C^\dagger\left( {{P_C}/{d_C}} \right)}}{{{{\mathit{\boldsymbol{\tilde V}}}_C}{\mathit{\boldsymbol{H}}_{CP}}{{\mathit{\boldsymbol{\tilde U}}}_P}\mathit{\boldsymbol{\tilde U}}_P^\dagger\mathit{\boldsymbol{H}}_{CP}^\dagger\mathit{\boldsymbol{\tilde V}}_C^\dagger\left( {{P_P}/{d_P}} \right) + {\mathit{\boldsymbol{I}}_{C{N_O}}}}}} \right|-\\ \log \left| {{\mathit{\boldsymbol{I}}_{{d_E}}} + \frac{{{{\mathit{\boldsymbol{\tilde V}}}_E}{\mathit{\boldsymbol{H}}_{EC}}{{\mathit{\boldsymbol{\tilde U}}}_E}\mathit{\boldsymbol{\tilde U}}_E^\dagger\mathit{\boldsymbol{H}}_{EC}^\dagger\mathit{\boldsymbol{\tilde V}}_E^\dagger\left( {{P_C}/{d_C}} \right)}}{{{{\mathit{\boldsymbol{\tilde V}}}_E}{\mathit{\boldsymbol{H}}_{EP}}{{\mathit{\boldsymbol{\tilde U}}}_P}\mathit{\boldsymbol{\tilde U}}_P^\dagger\mathit{\boldsymbol{H}}_{EP}^\dagger\mathit{\boldsymbol{\tilde V}}_E^\dagger\left( {{P_P}/{d_P}} \right) + {\mathit{\boldsymbol{I}}_{E{N_O}}}}}} \right| \end{array}$

(7)

基于式(7)，次用户的安全中断概率表示为

${P_{{\rm{out}}}} = \Pr \left\{ {{R_S} < {R_{{\rm{th}}}}} \right\}$

(8)

式中R_th表示次用户安全传输的速率门限值。

3 仿真分析

本节中，针对认知网络下的多用户对系统，利用Monte Carlo仿真验证本文给出的分布式计算干扰对准的发送和接收预编码矩阵方案的有效性，分析时假设主次用户具有相同的功率配置P_P=P_C，系统的安全传输速率门限为R_th=2。

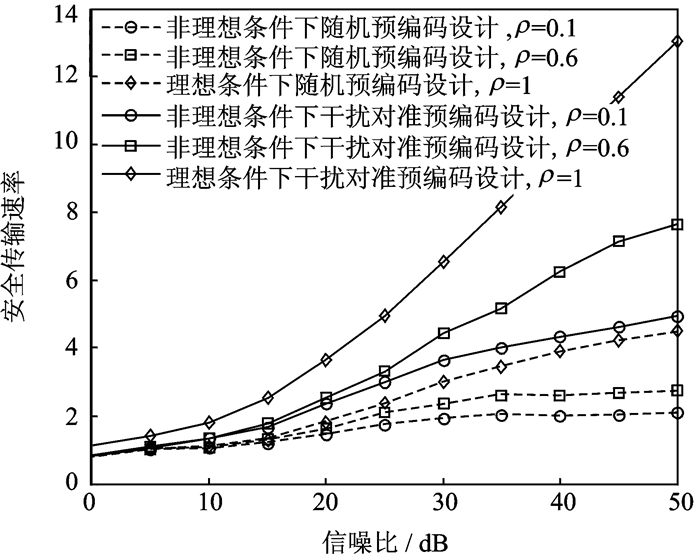
图 2给出了次用户的安全传输速率随SNR的变化情况。仿真时假定每个节点配备两根天线，也就是说每个节点的最大可达自由度为1。可以看出，非理想条件下经干扰对准后次用户系统的最大安全传输速率优于预编码矩阵随机给定时的传输速率，验证了干扰对准技术在提高存在窃听节点认知网络下的多用户对系统安全传输的有效性。显而易见，信道时延较小时最大安全传输速率会向理想条件下的最大安全传输速率逼近ρ=1。信道时延较大时的安全传输速率趋近于预编码矩阵随机给定下的安全传输速率曲线，这是因为此时求得的预编码矩阵与实际传输信道间的随机不相关性加大，从而逼近于预编码矩阵随机给定时的场景。

图 3给出了次用户的安全中断概率随SNR的变化情况。和图 2设定一样，假定每个节点配备两根天线。同样可以看出，在非理想条件下ρ≠1经干扰对准后次用户系统的中断概率性能优于预编码矩阵随机给定时的系统安全中断性能，验证了干扰对准技术在提高系统性能中的必要性。同时信道时时延误差较大时，经干扰对准下的安全中断概率也比较大，说明了信道估计的精度对系统设计有非常重要的影响。

4 结束语

为了估计干扰对准技术在下一代蜂窝移动通信系统中应用的可行性，本文基于存在窃听节点的信道非理想条件下的认知网络中的多用户对系统，以安全传输速率和安全中断概率为指标研究了系统的性能。仿真结果表明，非理想条件下经干扰对准后的系统性能明显优于预编码矩阵随机给定时的系统性能，验证文中理论分析的正确性。此外，随着信道时延误差的加大，系统的性能也会受到较大的影响，证实了信道估计精确度是未来系统设计时不可缺少的重要因素。