旋翼是直升机主要的气动力来源，旋翼的气动性能直接影响直升机的整体性能。为准确分析旋翼的气动性能，可以采用CFD 方法对旋翼流场进行计算^[1]。同时，由于直升机旋翼桨叶是细长柔性体，在气动载荷作用下会产生结构变形，因此需要在流场计算中引入CSD分析模块，以计入弹性变形导致的流场变化^[2]。而弹性旋翼周围的贴体网格是影响流场计算结果的重要方面。与固定翼相比，旋翼桨叶的结构运动要复杂得多，桨叶运动是直线和旋转运动的合成，且桨叶不仅有类刚性的整体运动，也包含了挥舞、摆振和变距(扭转)及轴向拉伸等多自由的弹性变形运动，这些运动之间存在复杂的耦合关系，桨叶运动的特殊性对旋翼周围的网格及流场求解均提出了很大挑战。因此，采用高精度动态网格变形技术在旋翼CFD/CSD耦合方法中进行旋翼气动特性数值模拟具有重要的意义^[3]。

早期的旋翼计算流体力学研究中对网格问题进行了简化处理，如仅采用桨叶近场的单块网格。随着多块嵌套网格方法及网格生成技术的不断发展，目前基于嵌套网格进行旋翼流场数值模拟已成为旋翼CFD 研究的主流^[4]。弹性旋翼流场的数值模拟虽然在近十多年内也取得了较大进展，但仍存在不少问题。其中，贴体网格的动态运动(变形)是模拟中一个很关键的方面，而目前的研究在这一方面尚处于发展之中，以致直接影响到数值模拟的精度。Datta等人^[5]采用的代数网格变形方法具有很高的效率，然而该方法网格变形生成后新旧两套网格上的流场物理量需要进行交换(插值)，同时三维情况可能存在网格单元扭曲过大的情况，这些原因导致CFD 方法的计算效率和精度有所损失。Batina等人^[6]最先提出了基于线性弹簧系统来模拟网格的方法。根据网格的结点连接关系，按一定规则给网格边赋予相应的刚度，则网格系统可以用一弹簧系统来模拟。然而网格结点在大变形条件下可能越过其相对面，造成网格畸形，方法失效。为了应对大变形问题，Farhat等人^[7]对弹簧模拟方法做了改进，在该方法中添加了非线性扭转弹簧，避免了原方法在某些情况下的失效现象。王海等人 ^[8]运用此方法对二维振荡翼型流场进行了验证，获得了较好的结果。综合研究表明，弹簧网格方法能够有效地解决网格变形过大的问题，但是目前该方法以二维网格应用为主，对于三维旋翼桨叶存在的复杂扭转、挥舞等弹性变形是否适用，需要进一步验证。

鉴于此，在旋翼CFD/CSD耦合分析研究中，为解决旋翼桨叶弹性变形后的三维网格生成问题，基于新型的弹簧模拟方法，引入“ball-vertex”冗余约束^[9]，即在结点与其对应面(边)之间添加相应的弹簧，考虑桨叶在刚性运动基础上的扭转、挥舞等弹性变形，规避流场物理量在网格变形前后的插值过程，并有效地避免出现畸形网格等问题。在旋翼CFD/CSD 耦合方法研究方面，分别对刚性旋翼流场分析(CFD)模块和旋翼结构动力学(CSD)模块进行了验证；然后，基于建立的桨叶三维网格变形方法，采用松耦合策略^[10]，计算了UH -60A直升机旋翼桨叶在前飞状态下的非定常气动载荷，并与试验结果及刚性CFD计算结果进行了对比，得到一些有意义的结论。

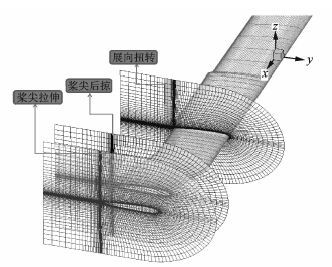
1 数值模拟方法 1.1 网格方法 1.1.1 网格生成方法

桨叶贴体结构网格采用C-H型网格。首先，生成绕二维翼型剖面的C型网格^[11]；然后，根据翼型展向分布规律，沿桨叶展向对C型网格进行平铺、缩放和扭转；最后，在桨根和桨尖处对C型网格(图 1)进行展向拉伸。C-H型网格桨根桨尖处理简单，对于根切比较小的桨叶网格而言，便于缩小桨根处网格内边界范围。

在进行前飞旋翼流场计算时，通常采用笛卡尔背景网格，并在与桨叶网格对应的区域进行适当加密，以精确获取旋翼区域传递的流场信息；同时尾迹区域相比于入流区域较大，可以更好地捕捉旋翼前飞时拖出的尾迹流场，准确地计算流场速度分布等信息。

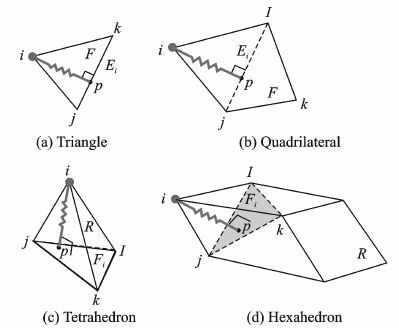
1.1.2 弹簧模拟网格变形方法

弹簧模拟方法最大的缺点是网格结点在大变形条件下可能越过其相对面(边)造成网格畸形，导致方法失效。为避免原方法失效情况的发生，不管对于何种网格，在任一网格结点构建一凸多面体(多边形)闭包，在结点与对应的闭包面之间引入冗余的“ball-vertex”约束弹簧，如图 2所示。在变形的过程中把该结点限制在该闭包范围之内，进而避免形成畸形网格，原弹簧模拟方法的失效情况也就不可能发生。

图 2中，点p为i点在一与其对应的三角形闭包面上的垂足，两点i与p之间的模拟弹簧上的作用力可以表示为

${{f}_{ip}}={{k}_{ip}}({{u}_{p}}-{{u}_{i}})\cdot {{n}_{ip}}\cdot {{n}_{ip}}=-{{f}_{pi}}$

(1)

式中：$\left\{ \begin{matrix} {{u}_{p}}={{c}_{1}}{{u}_{j}}+{{c}_{2}}~{{u}_{k}}+{{c}_{3}}{{u}_{l}} \\ {{k}_{ip}}=1/{{l}_{ip}} \\ {{l}_{ip}}={{r}_{ij}}\cdot {{r}_{ip}} \\ {{r}_{p}}={{r}_{i}}+{{r}_{ij}}\cdot {{n}_{ip}}{{n}_{ip}}~={{c}_{1}}{{r}_{j}}+{{c}_{2}}{{r}_{k}}+{{c}_{3}}{{r}_{l}} \\ \end{matrix} \right.$, 其中c₁, c₂, c₃为点p在三角形内的面积坐标，$\sum\limits_{i=1}^{3}{3{{c}_{~}}i=1,{{c}_{i}}={{S}_{i}}/S}$。

则该垂线单元的虚功可以表示为

$\delta W=-({{f}_{ip}}\cdot \text{ }\delta {{u}_{i}}+{{f}_{pi}}\cdot \delta \text{ }{{u}_{p}})={{\left( \delta u \right)}^{T}}Ku$

(2)

式中：$u={{[{{u}_{i}}~{{u}_{j}}~{{u}_{k}}~{{u}_{l}}]}^{T}};K=ACTA\text{ }=\text{ }{{k}_{ip~}}{{n}_{ip}}{{n}^{T}}_{ip}$。

系统的模拟刚度矩阵为

$K=\left[ \begin{array}{*{35}{l}} \cdots & {} & \cdots & {} & \cdots & {} & \cdots & {} & \cdots \\ {} & \sum {{k}_{ii}} & {} & \sum {{k}_{ij}} & {} & \sum {{k}_{i\text{ }k}} & {} & \sum {{k}_{il}} & {} \\ {} & {} & \cdots & {} & \cdots & {} & \cdots & {} & \cdots \\ {} & {} & {} & \sum {{k}_{jj}} & {} & \sum {{k}_{jk}} & {} & \sum {{k}_{jl}} & {} \\ {} & {} & {} & {} & \cdots & {} & \cdots & {} & \cdots \\ {} & {} & {} & {} & {} & \sum {{k}_{kk}} & {} & \sum {{k}_{kl}} & {} \\ {} & {} & {} & {} & {} & {} & \cdots & \cdots & \cdots \\ {} & {} & {} & {} & {} & {} & {} & \sum {{k}_{kk}} & {} \\ {} & {} & {} & {} & {} & {} & {} & {} & \cdots \\ \end{array} \right]$

(3)

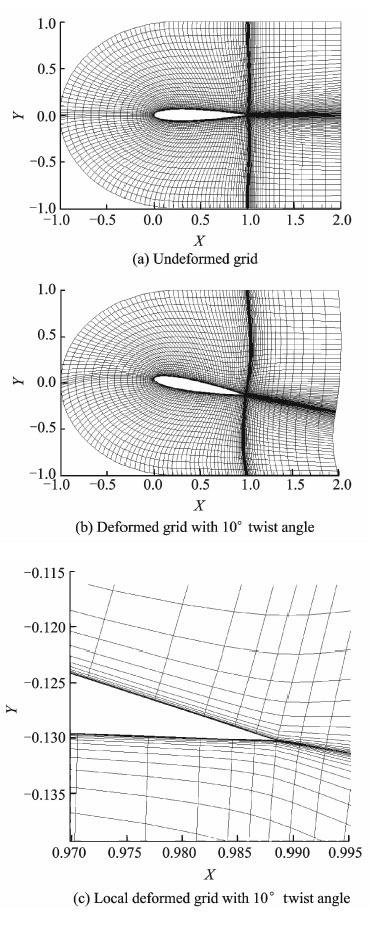
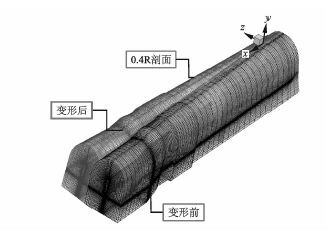
图 3(a)为围绕NA CA0012翼型的二维C型初始网格，图 3(b)对其进行了扭转(迎角变化)运动。图 4为围绕UH- 60A直升机旋翼三维贴体网格经过挥舞、摆振、变距(扭转)运动后的变形示意图。从图中的结果可以看出，尽管翼型后缘处网格变形比较大，然而“ball-vertex”方法能有效地避免了畸形网格的出现，并且保留了变形前附面层网格的贴体性和正交性，总体上表明这里建立的网格变形方法可以获得较好的网格质量。

1.2 流场计算方法

分别采用N-S方程和Euler方程对桨叶贴体网格区域和背景网格区域进行流场计算。控制方程采用以绝对物理量为参数的、守恒的积分形式的雷诺平均N-S方程

${{\frac{\partial }{\partial t}}_{\Omega }}Wd\Omega {{+}_{\partial \Omega }}(F-{{F}_{v}})dS=0$

(4)

式中：$W=\left\lfloor \begin{array}{*{35}{l}} \rho \\ \rho u \\ \rho v \\ \rho w \\ \rho E \\ \end{array} \right\rfloor ;F=\left\lfloor \begin{array}{*{35}{l}} \rho \text{ }{{V}_{r}} \\ \rho u{{V}_{r}}+{{n}_{x}}p \\ \rho v{{V}_{r}}+{{n}_{~}}yp \\ \rho w{{V}_{r}}+{{n}_{z}}p \\ \rho H{{V}_{r}}+{{V}_{t}}p \\ \end{array} \right\rfloor ;{{F}_{v}}~=\left\lfloor \begin{array}{*{35}{l}} 0 \\ {{n}_{x}}{{\tau }_{xx}}+{{n}_{y}}{{\tau }_{xy}}+{{n}_{z}}{{\tau }_{xz}} \\ {{n}_{x}}{{\tau }_{~}}yx+{{n}_{y}}\tau {{~}_{yy}}+{{n}_{z}}{{\tau }_{yz}} \\ {{n}_{x}}{{\tau }_{zx}}+{{n}_{y}}{{\tau }_{zy}}+{{n}_{z}}{{\tau }_{zz}} \\ {{n}_{x}}{{\theta }_{x}}~+{{n}_{y}}{{\theta }_{y}}+{{n}_{z}}{{\theta }_{z}} \\ \end{array} \right\rfloor $；Ω表示流场空间中任意控制体；∂Ω表示控制体Ω的边界；dS为∂Ω上的面元；n_x，n_y和n_z为dS 的单位面法矢；u，v和w为流体速度分量；p为流体压强；ρ为流体密度。

对控制方程量纲一化，选择来流空气密度、速度和平均气动弦长为基本量。通量计算采用Jameson二阶中心差分格式。为模拟旋翼前飞流场中的非定常流动，采用双时间法进行时间推进，湍流模型采用B-L模型^[12]。在选取边界条件时，物面边界采用无滑移条件，远场边界采用一维Riemann不变量来处理，旋翼桨叶网格和背景网格间的数据交换通过线性插值实现。

1.3 CSD方法

一维梁分析模型采用Hamilton变分原理建立旋翼桨叶运动方程，对于非保守系统，Hamilton原理的表达形式为

${{^{{{t}_{2}}}}_{{{t}_{1}}}}\left( \delta U-\delta T-\delta W \right)dt=0$

(5)

式中：δU 表示应变能的变分；δT表示动能的变分；δW表示外力虚功。

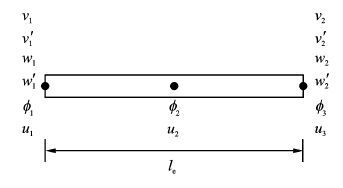
本文采用基于中等变形梁理论的14自由度梁单元模型^[13]，每个单元具有3个节点，分别位于单元两端和单元中点，其中端部节点具有v，v′_x，w，w′_x，φ，u六个自由度，中间节点具有φ，u两个自由度。梁单元如图 5所示。 其中，v和w自由度采用了两节点的Hermite插值，以保证两端节点处位移及其转角连续，而其他自由度采用三节点的Lagrange插值。

1.4 CFD/CSD耦合策略

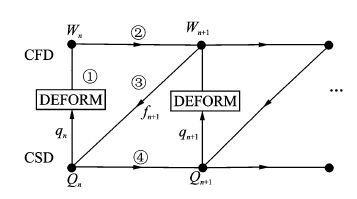
本文采用CFD/CSD松耦合方法进行流场和结构间的信息交换，主要包括两方面的内容：(1) 将旋翼动力学分析得到的桨叶运动变形，以边界条件的形式传递到网格变形中；(2) 将变形后的网格代入流场进行求解，得到桨叶表面压强分布，再以等效载荷的方式施加到对应的桨叶有限单元节点上，如图 6所示。

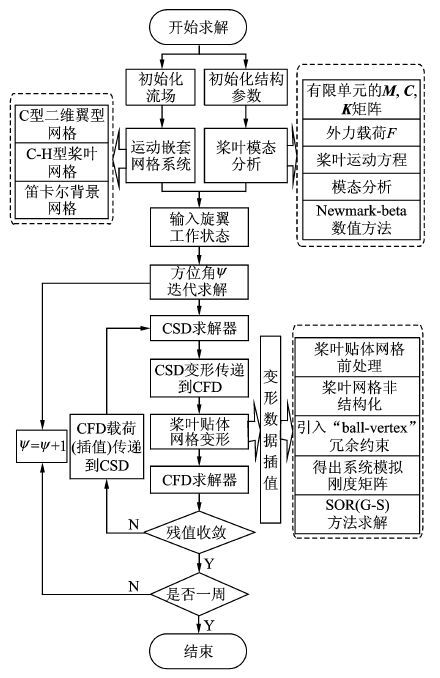
本文拟建立一套CFD/CSD松耦合计算方法，流程如图 7所示。松耦合策略是将CFD模块和CSD模块结合起来，旋翼每旋转一圈进行一次流场和结构间的信息交换。

2 模型验证 2.1 CFD模型验证

采用本文的网格变形方法对振荡NACA0012翼型的流场进行了求解。Ma=0.6，缩减频率k=0.0808，α=2.89°+2.41°sin(ωt)。

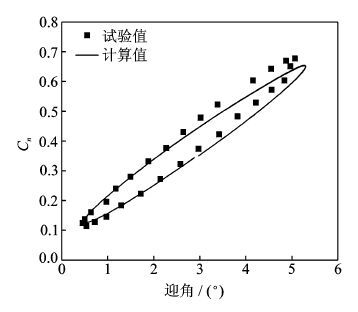
从图 8可以看出，翼型振荡的升力得到了比较好的模拟结果^[8]。可见，本文给出的网格变形方法合理、有效。

2.2 CSD模型验证

为验证CSD模块的有效性，采用具有详细结构参数的UH-60A直升机旋翼^[14]作为验证结构模型的算例。UH-60A直升机旋翼基本参数如表 1所示，其中的结构参数为UMARC软件^[15]的输入值。

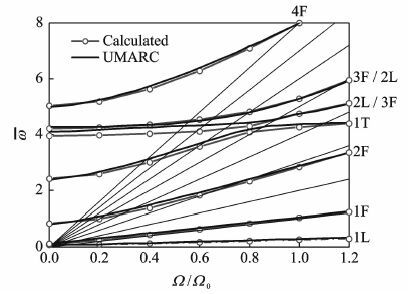
计算所得桨叶共振图如图 9所示。采用UMARC 软件计算得到的一阶摆振 (L)、 挥舞(F)

和扭转(T)频率分别为0.27，1.04和4.38，本文计算得到的相应频率为0.259 6 ，1.038和4.382。从图 9 可以看出，本文计算结果与UMARC软件计算结果在小转速下有一些误差，在工作转速下与UMARC软件计算结果吻合较好，表明CSD结构分析模块可以准确地计算前飞旋翼桨叶的固有特性，进而为CFD/CSD的松耦合计算提供基础。

3 数值模拟

采用CFD/CSD松耦合方法对弹性UH-60A直升机旋翼桨叶进行了载荷预测，计算了前进比为0.368时，旋翼桨叶压强系数分布与法向力系数分布，并与文献中的试验值^[16]进行对比，计算状态参数为：θ₀=13.55，θ_1c=3.39，θ_1s=-9.62。

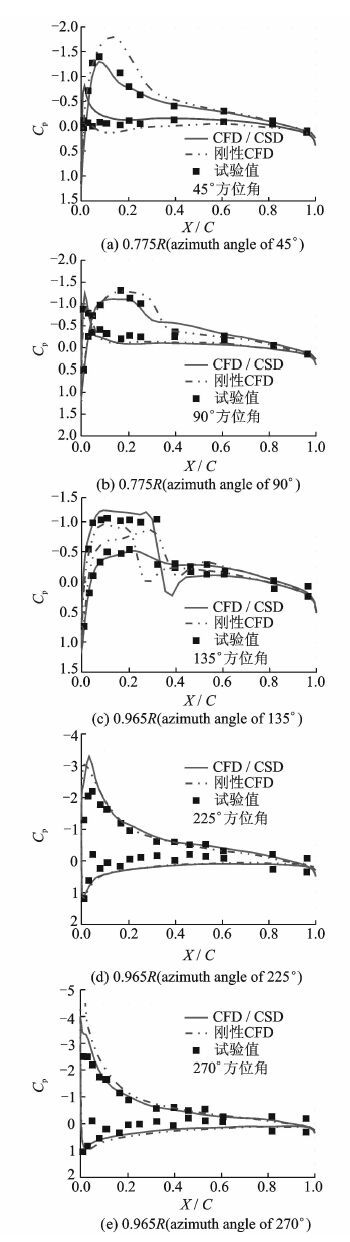
图 10为本文计算的UH-60A直升机旋翼r/R=0.775和r/R=0.965剖面压强系数分布与刚性CFD计算值和试验值的对比。从图中可以看出，与刚性CFD方法相比，CFD/CSD耦合方法可以得到与试验值更加吻合的结果。

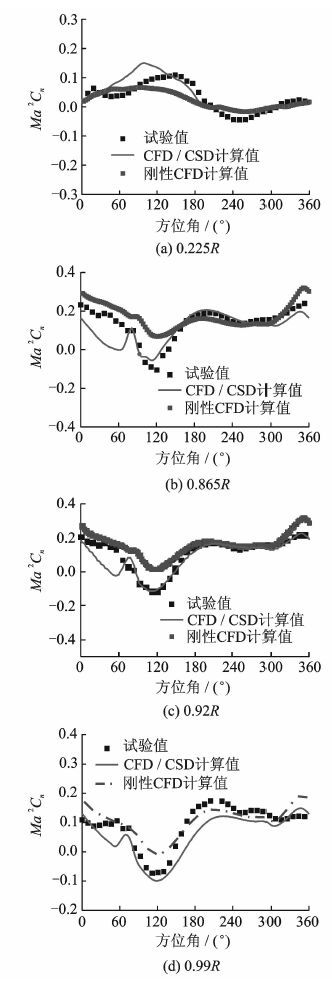
图 11(a～d)为本文计算的前进比0.368时UH-60A直升机旋翼展向不同剖面的法向力系数与试验值和刚性CFD方法计算结果的对比。可以看出，CFD/CSD耦合方法计算结果相对于刚性CFD方法的计算结果整体上与试验值更加吻合。CFD/CSD耦合方法的计算结果可以模拟出前行桨叶在60°～90°方位角桨尖处出现的微弱BVI(桨-涡干扰)现象；在90°～150°方位角处桨叶展向剖面升力变为负值，这主要与前行侧桨叶高马赫数下造成的激波失速等因素有关，采用CFD/CSD耦合计算结果可以很好地捕捉到这一现象；此外，本文计算的后行侧旋翼法向力系数在幅值与相位上均与试验值吻合较好，反映了法向力随方位角变化的整体趋势，体现了CFD/CSD耦合方法在前飞旋翼非定常气动力计算方面的优势。

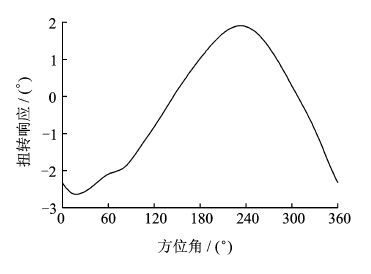
图 12为前飞状态旋翼0.92R剖面弹性扭转响应图。结合图 11(c) 法向力系数分布，从图 12可以看出：直升机高速飞行状态下，在旋翼前行侧0°～150°方位角，桨尖存在激波失速，从而形成负升力，对旋翼产生低头力矩，旋翼的扭转响应为负值，修正当地翼型剖面的气动迎角，150°～310°方位角，逐渐产生向上升力，扭转响应为正值，气动力增加，300°方位角以后扭转响应再次变为负值，而刚性CFD方法的计算结果由于未考虑桨叶弹性影响，在90°～180°方位角和310°～360°方位角计算求得的气动载荷与试验值存在一定偏差。

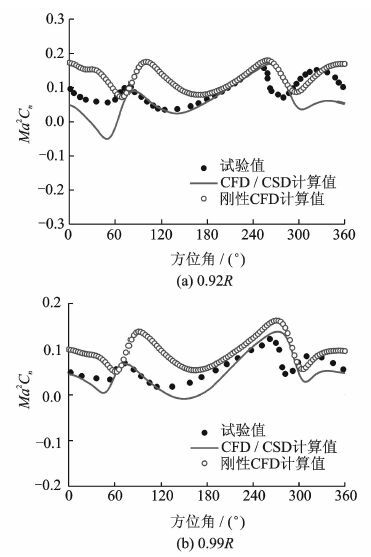
图 13(a，b)为本文计算的前进比0.15时UH-60A直升机旋翼展向不同剖面的法向力系数与试验值与刚性CFD方法计算结果的对比。由于前进比较小，在桨叶前行侧和后行侧发生较为严重的桨/涡干扰(BVI)现象，增加了对气动力预测的难度，而产生一定的误差，但采用CFD/CSD方法的旋翼载荷预测总体与试验值较为吻合，由于引入CSD 桨叶变形模块，在桨尖处产生的扭转力矩对桨叶产生了一定的扭转变形，修正了桨叶剖面的几何迎角，相对于刚性CFD计算结果，升力的幅值和相位更加精确。

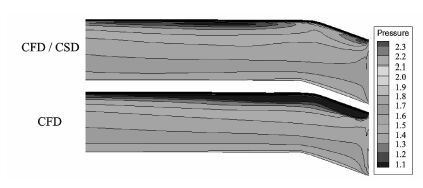
图 14为前行侧90°方位角处旋翼压强分布图，可以看出计入CSD变形后桨尖区域压强分布得到显著的缓和，说明本文引入的“ball-vertex”约束弹簧模拟网格变形方法可以有效地应用于直升机旋翼CFD/CSD耦合计算中。

4 结论

本文建立了一套适合于前飞旋翼CFD/CSD耦合计算的弹簧模拟网格变形方法，以UH-60A直升机旋翼为算例进行了前飞旋翼非定常载荷预测研究，得到以下结论：

(1) 引入的“ball-vertex”约束弹簧模拟网格变形方法可以有效避免畸形网格的出现，且变形后网格节点仍可以保持较好的贴体性和正交性。通过网格变形的算例、振荡翼型流场求解及前飞状态旋翼的非定常载荷计算结果表明该方法具有很好的鲁棒性和良好的计算精度。

(2) 与刚性CFD方法相比，建立的旋翼CFD/CSD耦合方法在直升机高速飞行状态下可以精确地捕捉到前行侧桨叶负升力现象和直升机低速飞行时产生的桨-涡干扰现象。

(3) 与刚性CFD方法相比，建立的旋翼CFD/CSD耦合方法可以较为精确地预测前飞状态直升机旋翼非定常气动载荷的相位和幅值。