直升机带外吊挂飞行能够克服直升机货舱对货物外形尺寸的限制,因此用途广泛。但在实际飞行中,超过10%的直升机飞行事故与吊挂飞行相关[1]。耦合是导致直升机吊挂飞行安全性不容乐观的一个重要因素。直升机本身存在严重的耦合,吊索和吊挂物的引入使得耦合更加严重。研究直升机吊挂飞行中的耦合对改善吊挂飞行安全具有重要意义。
针对直升机吊挂飞行耦合的研究由来已久且备受关注。Lucassen等[2]最早研究了直升机吊挂飞行中的耦合,建立了平面内的飞行动力学模型,分析了吊挂飞行对直升机动稳定性的影响。该研究中初步涉及了直升机和吊挂系统的耦合,模型相对简单。Strope等[3-6]均基于已有直升机飞行动力学模型,开发吊挂系统模块,将吊挂系统对直升机的影响处理成额外作用力,组建直升机吊挂飞行动力学模型。利用已有直升机模型,能大大减小工作量。Thanapalan等[7-10]基于飞行动力学模型分析了动稳定性对吊挂参数的敏感性。国内,齐万涛[11]、王照瑞[12]和曹龙[13]等也都建立了直升机吊挂飞行动力学模型并分析了吊挂飞行的动稳定性。动稳定性只是耦合的最终结果,直升机和吊挂系统相互耦合的机理有待更深入的研究。
建立全耦合的直升机吊挂飞行动力学模型是研究耦合的基础。除直升机本体外,吊挂飞行建模主要包括吊索和吊挂物模型。吊索的弹性系数通常较大,弹性吊索模型使整个系统趋于刚性,尤其在实时仿真中极易引起失真[14],刚性吊索模型在很多工程实践中更受青睐。从耦合分析的角度看,虽然弹性吊索比刚性吊索更符合物理实际,但是弹性吊索使得直升机和吊挂的耦合需要经历吊索弹性伸缩的中间过程,从而使得直升机和吊挂之间的耦合变得不够直接和清晰。因此,刚性吊索模型更有利于分析耦合。此时,为了研究耦合需要将直升机和吊挂系统通盘考虑建模,而不能仅在直升机模型加入作用力。大多研究中通常以标准箱体作为吊挂物[15-16],对应的模型是刚体模型。现有研究中很少有建立了能用于耦合分析的直升机/刚性吊索/刚体吊挂物的全耦合飞行动力学模型。目前对于直升机吊挂飞行的耦合分析,大多仅停留于动稳定性参数敏感性分析,而动稳定性只是系统耦合特性的综合反映。为了更深入认识直升机和吊挂系统的耦合,有必要深入到气动导数层面探讨耦合机理。
为了研究直升机吊挂飞行中的耦合,本文首先建立了全耦合的直升机/刚性吊索/刚体吊挂物飞行动力学模型。模型中通过可逆系数矩阵全面考虑惯性耦合同时有效回避微分代数混合方程组。然后计算配平特性和频响特性,通过与飞行试验数据对比验证模型精度。最后通过对比气动导数和动稳定性,分析直升机和吊挂系统的相互耦合。
1 直升机/吊索/吊挂物耦合建模 1.1 模型概述设直升机吊挂飞行系统的状态向量由直升机状态向量yH和吊挂系统状态向量yL组成。其中,直升机的状态向量yH为
| ${\mathit{\boldsymbol{y}}_{\rm{H}}} = {\left[ {{\mathit{\boldsymbol{\beta }}^{\rm{T}}}\;{{\mathit{\boldsymbol{\dot \beta }}}^{\rm{T}}}\;{\mathit{\boldsymbol{\upsilon }}^{\rm{T}}}\;{\mathit{\boldsymbol{V}}^{\rm{T}}}\;{\mathit{\boldsymbol{\omega}} ^{\rm{T}}}\;{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right]^{\rm{T}}}$ | (1) |
式中:β为不旋转系下的旋翼桨叶挥舞角位移,以4片桨叶为例,则β=[β0 β1c β1s βd]T;
由于吊挂物重力的作用,认为吊挂飞行中吊索始终处于紧绷状态。刚性吊索在绷紧状态吊索长度保持不变,即
| ${\mathit{\boldsymbol{y}}_{\rm{L}}} = {\left[ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}\;\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}_c^{\rm{T}}\;\mathit{\boldsymbol{\omega }}_{\rm{L}}^{\rm{T}}\;\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{L}}^{\rm{T}}} \right]^{\rm{T}}}$ | (2) |
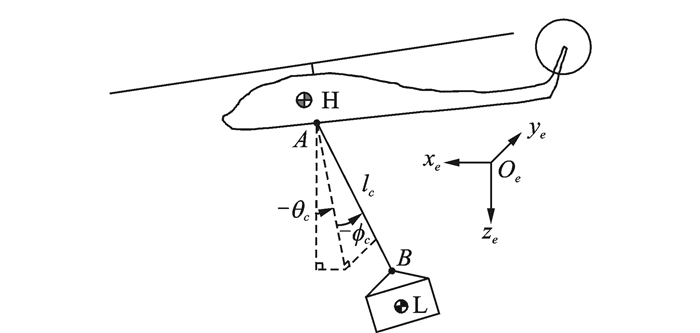
式中:Φc=[ϕc θc]T为吊索摆角,其定义如图 1所示。图 1中,长度为lc的吊索连接直升机 (H) 上的吊挂点A和吊挂物 (L) 上的吊挂点B,吊索与两个吊挂点均为铰接,吊索自身可自由扭转。在地轴系Oexeyeze下定义吊索的横向摆角ϕc和纵向摆角θc。式 (2) 中,ωL=[pL qL rL]T是吊挂物体轴系下的角速度,ΦL=[ϕL θL ψL]T是吊挂物的滚转、俯仰和偏航姿态。
|
图 1 吊挂系统示意图 Figure 1 Diagram of slung loadsystem |
状态空间形式的全耦合飞行动力学方程为
| $\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot y}}}_{\rm{H}}}}\\ {{{\mathit{\boldsymbol{\dot y}}}_{\rm{L}}}} \end{array}} \right] = {\mathit{\boldsymbol{C}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{\rm{H}}}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}},\mathit{\boldsymbol{\delta }}} \right)}\\ {{\mathit{\boldsymbol{f}}_{\rm{L}}}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}}} \right)} \end{array}} \right]$ | (3) |
式中:向量函数fH和fL均与状态向量导数无关;t为时间;操纵向量δ=[θ0 θ1c θ1s θt]T包含直升机的总距、横向周期变距、纵向周期变距和尾桨总距。可逆系数矩阵C为
| $\mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_{{\rm{HH}}}}}&{{\mathit{\boldsymbol{C}}_{{\rm{HL}}}}}\\ {{\mathit{\boldsymbol{C}}_{{\rm{LH}}}}}&{{\mathit{\boldsymbol{C}}_{{\rm{LL}}}}} \end{array}} \right]$ | (4) |
式中:非对角系数矩阵CHL和CLH为直升机和吊挂系统的惯性耦合所致;fH与yL相关,且fL与yH相关,这是直升机和吊挂系统的气动和惯性耦合所致。本文建模中将刚性吊索的长度约束作为已知条件代入推导,而不作为独立的几何约束方程,并因此得出可逆系数矩阵C,在完整考虑了惯性耦合的同时避免了代数微分混合方程组的出现,降低了求解难度。
1.2 直升机飞行动力学建模直升机飞行动力学模型主要由铰接式旋翼、尾桨、机身、平尾和垂尾这几个部件模型,部件间的气动干扰模型以及机体六自由度刚体动力学模型组成。旋翼模型中主要包括桨叶的准定常气动力模型、刚体桨叶的挥舞动力学模型以及旋翼的Pitt-Peters动态入流模型[17]。桨叶气动力由叶素气动力累加得到,而叶素气动力根据叶素当地气流环境插值翼型气动力数据获得。刚体桨叶的挥舞动力学模型根据达朗贝尔原理建立。尾桨模型中主要包括尾桨的气动力模型和均匀入流模型,其气动力的计算类似于旋翼。机身、平尾和垂尾模型中主要包括各自的准定常气动力模型,气动力的计算依靠风洞数据或经验公式。基于风洞试验和经验的部件间气动干扰模型中主要包括旋翼对其余部件的下洗模型以及机身对尾桨、平尾和垂尾的侧洗和动压损失模型等。各部件将对直升机重心产生六力素,由此而建立机体的六自由度刚体动力学模型。此外,直升机飞行动力学模型中还包括描述直升机姿态变化的运动学关系方程[18]。
在直升机飞行动力学模型中,因耦合对式中系数矩阵C具有贡献的是旋翼刚体挥舞动力学模型和机体六自由度刚体动力学模型,下面对这两个模型逐一展开。
由所有桨叶的挥舞动力学方程联立得到旋翼桨叶挥舞动力学方程为
| $\mathit{\boldsymbol{C}}_{\ddot \beta }^{\ddot \beta }\mathit{\boldsymbol{\ddot \beta + C}}_{\ddot \beta }^{\dot V}\mathit{\boldsymbol{\dot V + C}}_{\ddot \beta }^{\dot \omega }\mathit{\boldsymbol{\dot \omega = }}{\mathit{\boldsymbol{f}}_{\ddot \beta }}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},\mathit{\boldsymbol{\delta }}} \right)$ | (5) |
式中:向量函数
类似地,机体六自由度动力学方程为
| $\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}}_{\dot V}^{\ddot \beta }}&{\mathit{\boldsymbol{C}}_{\dot V}^{\dot V}}&{\mathit{\boldsymbol{C}}_{\dot V}^{\dot \omega }}&{\mathit{\boldsymbol{C}}_{\dot V}^{\dot \omega }{\rm{L}}}\\ {\mathit{\boldsymbol{C}}_{\dot \omega }^{\ddot \beta }}&{\mathit{\boldsymbol{C}}_{\dot \omega }^{\dot V}}&{\mathit{\boldsymbol{C}}_{\dot \omega }^{\dot \omega }}&{\mathit{\boldsymbol{C}}_{\dot \omega }^{\dot \omega }{\rm{L}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot \beta }}}\\ {\mathit{\boldsymbol{\dot V}}}\\ {\mathit{\boldsymbol{\dot \omega }}}\\ {{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{L}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{\dot V}}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}}\mathit{\boldsymbol{,\delta }}} \right)}\\ {{\mathit{\boldsymbol{f}}_{\dot \omega }}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}}\mathit{\boldsymbol{,\delta }}} \right)} \end{array}} \right]$ | (6) |
式中:向量函数
由吊索和吊挂物组成的吊挂系统模型中主要包括吊索摆动动力学方程、吊挂物角运动方程以及描述吊挂物姿态变化的运动学方程。前两者中存在较复杂的耦合。
根据图 1的定义,可得运动学关系
| ${\mathit{\boldsymbol{V}}_{\rm{L}}} = {\mathit{\boldsymbol{\tilde R}}_{LB\omega {\rm{L}}}} + {\mathit{\boldsymbol{A}}_{\rm{L}}}\left[ {{{\mathit{\boldsymbol{\dot R}}}_{AB}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{V}} - {{\mathit{\boldsymbol{\tilde R}}}_{HA\omega }}} \right)} \right]$ | (7) |
式中:VL为吊挂物体轴系下吊挂物重心处的速度;RLB为吊挂物体轴系下从重心L指向吊挂点B的位置向量;上标“~”表示向量的坐标方阵;AL为地轴系到吊挂物体轴系的转换矩阵;RAB为地轴系下吊挂点A指向吊挂点B的位置向量;
建立吊挂物的力平衡方程,代入上述运动学关系,并消去其中的吊索张力,可得到如下吊索摆角动力学方程
| $\mathit{\boldsymbol{C}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}^{\dot V}\mathit{\boldsymbol{\dot V}} + \mathit{\boldsymbol{C}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}^{\dot \omega }\mathit{\boldsymbol{\dot \omega }} + {\mathit{\boldsymbol{ \boldsymbol{\ddot \varPhi} }}_c} + \mathit{\boldsymbol{C}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}^{\dot \omega }{\rm{L}}{\mathit{\boldsymbol{\dot \omega }}_{\rm{L}}} = {\mathit{\boldsymbol{f}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}}} \right)$ | (8) |
式中:等号左端的3个系数矩阵分别为
| $\begin{array}{l} \mathit{\boldsymbol{C}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}^{\dot V} = {\mathit{\boldsymbol{C}}_{CL1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\\ \mathit{\boldsymbol{C}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}^{\dot \omega } = - {\mathit{\boldsymbol{C}}_{CL1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde R}}}_{HA}}\\ \mathit{\boldsymbol{C}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}^{{{\dot \omega }_L}} = {\mathit{\boldsymbol{C}}_{CL1}}\mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{{\mathit{\boldsymbol{\tilde R}}}_{LB}} \end{array}$ | (9) |
方程右端的向量函数为
| $\begin{array}{l} \;\;\;\;\;\;\;{\mathit{\boldsymbol{f}}_{{{\mathit{\ddot \Phi }}_\mathit{c}}}}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}}} \right) = \\ \;\;\;\;{\mathit{\boldsymbol{C}}_{CL0}} + \frac{{{\mathit{\boldsymbol{C}}_{CL1}}\mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{F}}_{OL}}}}{{{m_{\rm{L}}}}} - \\ {\mathit{\boldsymbol{C}}_{CL1}}\left[ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\tilde \omega \left( {\mathit{\boldsymbol{V}} - {{\mathit{\boldsymbol{\tilde R}}}_{HA}}\omega } \right) + \mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{{\mathit{\boldsymbol{\tilde \omega }}}_{\rm{L}}}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{\omega }}_{\rm{L}}}} \right] \end{array}$ | (10) |
式中:mL为吊挂物质量;FOL为吊挂物体轴系下作用于吊挂物的重力和气动力之和。式 (9, 10) 中的CCL0和CCL1分别为
| $\begin{array}{l} {\mathit{\boldsymbol{C}}_{CL0}} = \left( \begin{array}{l} - \sin {\phi _c}\cos {\phi _c} \cdot \dot \theta _c^2\\ 2\tan {\phi _c} \cdot {{\dot \phi }_c}{{\dot \theta }_c} \end{array} \right)\\ {\mathit{\boldsymbol{C}}_{CL1}} = \frac{1}{{{l_c}}}\left( {\begin{array}{*{20}{l}} { - \sin {\phi _c}\sin {\theta _c}}&{ - \cos {\phi _c}}&{ - \sin {\phi _c}\cos {\theta _c}}\\ {\cos {\theta _c}\sec {\phi _c}}&0&{ - \sin {\theta _c}\sec {\phi _c}} \end{array}} \right) \end{array}$ |
式 (8) 表明,除了吊挂物自身的气动力和重力,直升机的运动和吊挂物的角运动均对吊索的摆动产生影响,因此耦合严重。
将式求得的
| $\begin{array}{l} {\mathit{\boldsymbol{F}}_{Hc}} = {m_{\rm{L}}}\left( {\dot \phi _c^2 + {{\cos }^2}{\phi _c}\dot \theta _c^2} \right)\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{AB}} + \\ l_c^{ - 2}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}\mathit{\boldsymbol{A}}_L^{\rm{T}}\left( {{\mathit{\boldsymbol{F}}_{OL}} - {m_{\rm{L}}}{{\mathit{\boldsymbol{\tilde \omega }}}_{\rm{L}}}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{\omega }}_{\rm{L}}}} \right) - \\ {m_{\rm{L}}}l_c^{ - 2}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\tilde \omega \left( {\mathit{\boldsymbol{V}} - {{\mathit{\boldsymbol{\tilde R}}}_{HA}}\mathit{\boldsymbol{\omega }}} \right) + \\ \left( { - {m_{\rm{L}}}l_c^{ - 2}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)\mathit{\boldsymbol{\dot V}} + \\ \left( {{m_{\rm{L}}}l_c^{ - 2}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde R}}}_{HA}}} \right)\mathit{\boldsymbol{\dot \omega }} + \\ \left( { - {m_{\rm{L}}}l_c^{ - 2}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}\mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}} \right){{\mathit{\boldsymbol{\dot \omega }}}_{\rm{L}}} \end{array}$ | (11) |
式中:FHc被分成两部分,前一部分与状态量导数无关,这将是吊索张力对式中
作用于吊挂点A处的吊索张力和作用于吊挂点B处的吊索张力,大小相等,方向相反。因此,吊索张力对吊挂物重心产生的力矩为
| $\mathit{\boldsymbol{C}}_{{{\dot \omega }_{\rm{L}}}}^{\dot V}\mathit{\boldsymbol{\dot V}} + \mathit{\boldsymbol{C}}_{{{\dot \omega }_{\rm{L}}}}^{\dot \omega }\mathit{\boldsymbol{\dot \omega }} + \mathit{\boldsymbol{C}}_{{{\dot \omega }_{\rm{L}}}}^{{{\dot \omega }_{\rm{L}}}}{\mathit{\boldsymbol{\dot \omega }}_{\rm{L}}} = {\mathit{\boldsymbol{f}}_{{{\dot \omega }_{\rm{L}}}}}\left( {t,{\mathit{\boldsymbol{y}}_{\rm{H}}},{\mathit{\boldsymbol{y}}_{\rm{L}}}} \right)$ | (12) |
式中:等号左端3个系数矩阵分别为
| $\begin{array}{l} \mathit{\boldsymbol{C}}_{{{\dot \omega }_{\rm{L}}}}^{\dot V} = - {m_{\rm{L}}}l_c^{ - 2}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\\ \mathit{\boldsymbol{C}}_{{{\dot \omega }_{\rm{L}}}}^{\dot \omega } = {m_{\rm{L}}}l_c^{ - 2}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde R}}}_{HA}}\\ \mathit{\boldsymbol{C}}_{{{\dot \omega }_{\rm{L}}}}^{{{\dot \omega }_{\rm{L}}}} = {I_{\rm{L}}} - {m_{\rm{L}}}l_c^{ - 2}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}\mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{{\mathit{\boldsymbol{\tilde R}}}_{LB}} \end{array}$ | (13) |
等号右边的的向量函数为
| $\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{{{\dot \omega }_{\rm{L}}}}} = {\mathit{\boldsymbol{M}}_{OL}} - {{\mathit{\boldsymbol{\tilde \omega }}}_{\rm{L}}}{\mathit{\boldsymbol{I}}_{\rm{L}}}{\omega _{\rm{L}}} - }\\ {l_c^{ - 2}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}\mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{\mathit{\boldsymbol{F}}_{OL}} - }\\ {{m_{\rm{L}}}\left( {\dot \phi _c^2 + {{\cos }^2}{\phi _c}\dot \theta _c^2} \right){{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}} + }\\ {{m_{\rm{L}}}l_c^{ - 2}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}\mathit{\boldsymbol{A}}_{\rm{L}}^{\rm{T}}{{\mathit{\boldsymbol{\tilde \omega }}}_{\rm{L}}}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\omega _{\rm{L}}} + }\\ {{m_{\rm{L}}}l_c^{ - 2}{{\mathit{\boldsymbol{\tilde R}}}_{LB}}{\mathit{\boldsymbol{A}}_{\rm{L}}}{\mathit{\boldsymbol{R}}_{AB}}\mathit{\boldsymbol{R}}_{AB}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\tilde \omega }}\left( {\mathit{\boldsymbol{V}} - {{\mathit{\boldsymbol{\tilde R}}}_{HA}}\omega } \right)} \end{array}$ | (14) |
式中:IL为刚体吊挂物的惯性矩矩阵;MOL为吊挂物体轴系下作用于吊挂物重心处的气动力矩。式 (12~14) 表明直升机机体运动以及吊索摆角运动均对吊挂物的角运动产生了耦合
2 模型验证通过将配平和频响的计算值与试验数据对比验证模型,以说明所建模型能用于耦合分析。
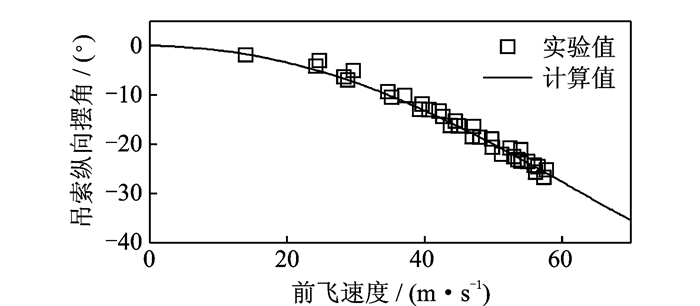
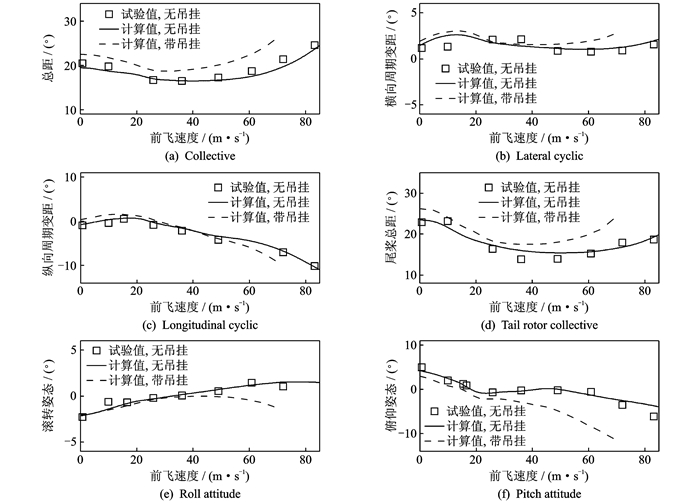
2.1 配平特性验证以UH-60直升机和CONEX箱体吊挂物为例,根据文献[19, 20]中的构型参数和飞行状态参数,计算配平特性。图 2中给出了吊索纵向摆角配平值随前飞速度的变化。随着前飞速度增加,吊挂物的气动阻力增加,吊索后摆角因此增加。图 2中的计算值和飞行试验值[21]吻合较好。直升机的操纵量和姿态配平值如图 3所示。由于带吊挂飞行的相关配平试验数据缺乏,图中给出了不带吊挂的计算值和飞行试验值[20],以及带吊挂的计算值。对比不带吊挂的飞行试验值和本文计算值,吻合较好。算例中,吊挂点A位于直升机重心前下方,为了平衡吊挂物的重力和气动阻力,吊挂飞行时图 3中的总距和尾桨总距均相应增加,滚转和俯仰力矩的平衡也使得横向和纵向周期变距发生了相应的变化,而侧向力和纵向力的平衡使得直升机的滚转和俯仰姿态也相应增加。图中所反映的这些区别是合理可信的。
|
图 2 吊索纵向摆角 (θc) 配平特性 Figure 2 Trim property of longitudinal cable angle (θc) |
|
图 3 直升机配平特性 Figure 3 Trim properties of helicopter |
2.2 频响特性验证
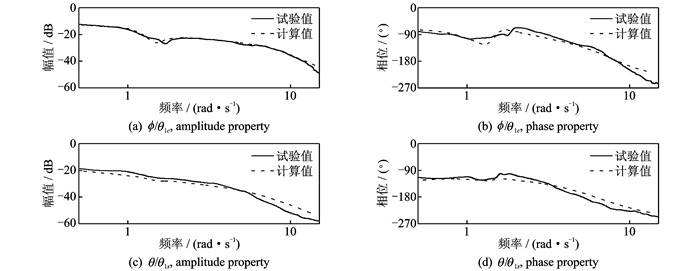
配平反映了系统的稳态特性,本节计算系统的幅频和相频特性,验证系统的动态特性。仍以前文UH-60直升机和CONEX箱体吊挂物为例。直升机不带吊挂以15 m/s速度前飞的姿态频响特性如图 4所示。图 4(a,b) 分别为直升机滚转姿态 (ϕ) 对横向周期变距 (θ1c) 的幅值特性和相位特性,图 4(c,d) 分别为直升机俯仰姿态 (θ) 对纵向周期变距 (θ1s) 的幅值特性和相位特性。图 5中给出了直升机带吊挂以15 m/s速度前飞时的频响特性。两图中,计算值和试验值[22]均较吻合。对比图 4,5可知,吊挂飞行对直升机的姿态频响特性具有显著影响。

|
图 4 直升机频响特性 Figure 4 Frequency response property of helicopter |
|
图 5 直升机吊挂飞行频响特性 Figure 5 Frequency response property of helicopter with slung load |
3 耦合分析
前文建模中充分考虑了直升机和吊挂系统的耦合,这种耦合直观表现为气动导数的变化,并进而影响系统的动稳定性。
基于配平状态对式“小扰动”线化,可得到直升机吊挂飞行的气动导数矩阵。为了更方便地对比,首先对系统减缩,缩小系统维数。基于弱耦合假设并兼顾挥舞和入流动特性的影响,对β,
沿用前文模型验证中的算例,对比分析15 m/s前飞时算例直升机与吊挂系统耦合和不耦合两种情形下的气动导数。其中,不耦合情形下的吊挂系统指的是吊挂飞行中直升机不受吊挂系统影响始终以恒定速度前飞时的吊挂系统[24],不耦合情形下的直升机即为不带吊挂飞行的直升机。耦合情形则指直升机与吊挂系统相互耦合。对比发现,在19×19的气动导数矩阵中,近半数的气动导数发生了变化。其中部分气动导数的变化相对显著,在表 1中列出。表中导数后括号内为导数变化量,“+”表示值增加,“-”表示值减小。其余导数的变化量远没有表中列出的导数显著。气动导数可分为4类:直升机自身、吊挂对直升机的耦合、直升机对吊挂的耦合以及吊挂自身。分别指直升机状态量变化率对自身状态量的导数、直升机状态量变化率对吊挂系统状态量的导数、吊挂系统状态量变化率对直升机状态量的导数以及吊挂系统状态量变化率对其自身状态量的导数。
| 表 1 吊挂飞行耦合导致的变化显著的气动导数 Table 1 Aerodynamic derivatives significantly influenced by couplings of flights with slung load |
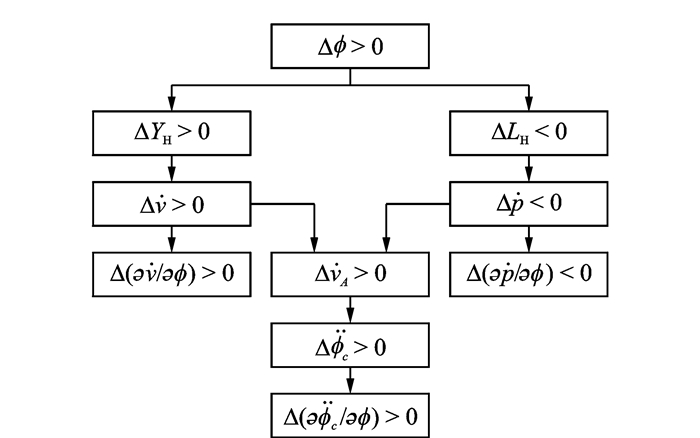
由表 1可知,除了
|
图 6 横向气动导数耦合机理 Figure 6 Coupling mechanism of lateral derivatives |
由气动导数的变化可以看出,吊挂系统通过作用于直升机上吊挂点处的作用力影响直升机,而直升机通过吊挂点的运动影响吊挂系统,相互耦合由此而建立。这种相互耦合改变了气动导数矩阵,也因此会对系统的动稳定性产生影响。
3.2 动稳定性的耦合分析表 2所示为15 m/s前飞时不耦合和耦合两种情形下直升机和吊挂系统各模态的动稳定性 (除直升机航向模态)。表 2中,“[ωn, ζ]”描述模态特征值为复根的模态固有频率ωn和阻尼比ζ,“(a)”描述特征值为实根-a的模态[20, 23]。不耦合情形下,直升机的运动模态包括以滚转角运动为主的滚转模态、以俯仰角运动为主的俯仰模态、以横向运动和滚转角运动为主的荷兰滚模态、以纵向运动和俯仰角运动为主的沉浮模态、以垂向运动为主的垂向模态以及以偏航角运动为主的螺旋模态。吊挂系统的运动模态包括以吊挂物滚转角运动为主的吊挂物滚转模态、以吊挂物俯仰角运动为主的吊挂物俯仰模态、以吊索横向摆动为主的吊挂横向单摆模态、以吊索纵向摆动为主的吊挂纵向单摆模态以及以吊挂物偏航角运动为主的吊挂物航向模态。耦合情形下,吊挂系统的状态量将参与到直升机的运动模态中,直升机的状态量也将参与到吊挂系统的运动模态中,运动模态的动稳定性也将随之而发生变化。
| 表 2 直升机吊挂飞行中的耦合对动稳定性的影响 Table 2 Effects of couplings on dynamic stability in helicopter flights w ith slung load |
对比表 2中耦合和不耦合两种情形下各运动模态的动稳定性可知,直升机运动模态中,滚转模态的稳定性被削弱近2/5,而荷兰滚模态的阻尼比也减小近1/4,文献[15]中也有类似发现。这两个模态中,滚转阻尼扮演了重要角色,吊挂飞行使得原先直升机自身的阻尼需同时对直升机和吊挂物起作用,稳定性因此被削弱。直升机垂向模态的变化很小。其余直升机模态稳定均略有改善,由前述气动导数可知,这是因为吊挂飞行增强了直升机姿态对角运动的静稳定性作用。
直升机和吊挂系统的耦合使得所有吊挂系统运动模态的稳定性均有所改善,其中尤以两个单摆模态最显著。吊挂横向单摆模态的阻尼比增加了7倍多,吊挂纵向单摆模态的阻尼比也增加了4倍多,稳定性得到了显著改善,文献[9, 15]中亦得到类似结果。在这两个单摆模态中,由于耦合气动导数,吊挂系统的运动会改变吊索作用于直升机上吊挂点处的作用力,激起直升机的运动,促使直升机自身的阻尼发生作用,从而增强运动模态的动稳定性。与此同时,由于直升机和吊挂系统的耦合,等效摆长变小,导致两个单摆模态的频率增加。
进一步分析发现,横航向运动模态的变化大于纵向运动模态,说明直升机和吊挂系统的横航向耦合强于纵向耦合。这与前文气动导数的耦合分析结果相一致。
4 结束语本文建立了能够用于耦合分析的直升机/刚性吊索/刚体吊挂物的全耦合飞行动力学模型,计算了直升机吊挂飞行的配平特性和频响特性,并通过与飞行试验数据对比验证了模型。
吊挂系统通过吊索作用于直升机上吊挂点处的作用力影响直升机,直升机通过吊挂点的运动影响吊挂系统,两者形成相互耦合。算例分析表明,直升机和吊挂系统的相互耦合,一方面使得直升机自身的阻尼需要对直升机和吊挂系统产生作用,另一方面使得直升机姿态对直升机角运动起静稳定作用同时增强了吊索摆角对吊索摆动的静稳定作用。直升机滚转模态和荷兰滚模态的稳定性因此被削弱,两个单摆模态的稳定性因此得到显著改善。而且直升机和吊挂系统的横航向耦合强于纵向耦合。
| [1] | MANWARING J C, CONWAY G A, GARRETT L C. Epidemiology and prevention of helicopte r external load accidents[J]. Journal of Safety Research, 1998, 29(2): 107–121. DOI:10.1016/S0022-4375(98)00007-3 |
| [2] | LUCASSEN L R, STERK F J. Dynamic stability analysis of a hovering helicopter with a sling load[J]. Journal of the American Helicopter Society, 1965, 10(2): 6–12. DOI:10.4050/JAHS.10.6 |
| [3] | STROPE K, GASSAWAY B, HARDING J. Frequency domain verification & validati on of a UH-60A FLIGHTLAB® model with a CONEX sling load[C]//Proceedings of the American Helicopter Society 61st Annual Forum. Grapevine, USA: the American Helicopter Society International, 2005. |
| [4] | KENDRICK S A, WALKER D J. The modelling simulation and control of helicopters operating with external loads[C]//Proceedings of the American Helicopter Society 62nd Annual Forum. Phoenix, USA: the American Helicopter Society Interna tional, 2006. |
| [5] | IVLER C M, TISCHLER M B, POWELL J D. Cable angle feedback control systems to improve handling qualities for helicopters with slung loads[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Portland, USA: AIAA, 2011. |
| [6] | GURSOY G, TARIMCI O, YAVRUCUK I. Helicopter slung load simulations using Heli-Dyn+[C]//AIAA Modeling and Simulation Technologies Conference. Minneapol is, USA: AIAA, 2012: 4851. |
| [7] | THANAPALAN K, WONG T M. Modeling of a helicopter with an under-slung loa dsystem[C]//Proceedings of the 29th Chinese Control Conference. Beijing, Chin a: IEEE, 2010: 1451-1456. |
| [8] | OKTAY T, SULTAN C. Modeling and control of a helicopter slung-loadsystem[J]. Aerospace Science and Technology, 2013, 29(1): 206–222. DOI:10.1016/j.ast.2013.03.005 |
| [9] | GUGLIERI G, MARGUERETTAZ P. Dynamic stability of a helicopter with an external suspended load[J]. Journal of the American Helicopter Society, 2014, 59(4): 1–12. |
| [10] | KRISHNAMURTHI J, HORN J F. Helicopter slung load control using lagged cable angle feedback[J]. Journal of the American Helicopter Society, 2015, 60(2): 1–12. |
| [11] |
齐万涛, 陈仁良.
直升机吊挂飞行稳定性和操纵性分析[J]. 南京航空航天大学学报, 2011, 43(3): 406–412.
QI Wantao, CHEN Renliang. Stability and control characteristic ana lysis for flight of helicopter with slung-load[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(3): 406–412. |
| [12] |
王照瑞, 曹义华.
吊挂物为刚体模型的直升机外吊挂飞行平衡与稳定性分析[J]. 南京航空航天大学学报, 2015, 47(2): 296–303.
WANG Zhaorui, CAO Yihua. Equilibrium characteristics and stability analysis of helicopter with rigid-body modeling slung-load[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(2): 296–303. |
| [13] |
曹龙, 曹义华, 李春华.
直升机-吊挂耦合系统平衡特性和稳定性分析[J]. 北京航空航天大学学报, 2014, 40(9): 1220–1225.
CAO Long, CAO Yihua, LI Chunhua. Equilibrium characteristics and stability analysis of helicopter-slung-load coupling system[J]. Journal of Be ijing University of Aeronautics & Astronautics, 2014, 40(9): 1220–1225. |
| [14] | CICOLANI L S, KANNING G. Equations of motion of slung load sys tems, including multi-lift systems[R]. NASA Technical Paper 3280, 1992. |
| [15] | RONEN T. Dynamics of a helicopter with a sling load[D]. Cali fornia, USA: Stanford University, 1986. |
| [16] | EHLERS G E. Hi-fidelity simulation and prediction of helicopt er single point external load stabilization[D]. California, USA: Naval Postgra duate School, 2001. |
| [17] | ZHAO J. Dynamic wake distortion model for helicopter maneuveri ng flight[D]. Altlanta, USA: Georgie Institute of Technology, 2005. |
| [18] |
高正, 陈仁良.
直升机飞行动力学[M]. 北京: 科学出版社, 2003: 43-53.
GAO Zheng, CHEN Renliang. Helicopter flight dynamics[M]. Beijing: Science Press, 2003: 43-53. |
| [19] | HOWLETT J J. UH-60A Black Hawk engineering simulation program : Volume I-Mathematical model final report[R]. NASA Contractor Report 166309, 1981. |
| [20] | KIM F D. Formulation and validation of high-order mathematica l models of helicopter flight dynamics[D]. City of College Park, USA: University of Maryland, 1991. |
| [21] | CICOLANI L S, LUSARDI J, GREAVES L D, et al. Flight test resul ts for the motions and aerodynamics of a cargo container and a cylindrical slung load[R]. NASA/TP-2010-216380, 2010. |
| [22] | TYSON P H. Simulation validation and flight prediction of UH-60A Black Hawk helicopter/slung load characteristics[D]. Monterey, USA: Naval Postgraduate School, 1999. |
| [23] | PADFIELD G D. Helicopter flight dynamics: The theory and appli cation of flying qualities and simulation modelling[M]. 2nd ed. Washington DC, USA: American Institute of Aeronautics and Astronautics, Inc, 2007: 236-251. |
| [24] | FEASTER L, POLI C, KIRCHHOFF R. Dynamics of a slung load[J]. Journal of Aircraft, 1977, 14(2): 115–121. DOI:10.2514/3.44578 |
 2017, Vol. 49
2017, Vol. 49


