可靠性分析中,经常需要由离散的实验数据求出概率分布曲线,进而计算可靠度。最大熵原理是解决概率类问题的有力工具,具有在拟合概率密度公式时不事先假定概率分布,公式统一,适用性强等优点。
文献[1~5]应用非线性最小二乘法+拟牛顿法确定最大熵概率密度公式中的拉格朗日乘子。但由于拉格朗日优化函数的高度非线性且拟牛顿法的局限性,使确定拉格朗日乘子时容易计算不收敛且结果受初始点选择影响较大。文献[6, 7]提出将拉格朗日优化函数积分区间进行线性变换,避免计算拉格朗日乘子时出现计算溢出情况,但在计算过程中需进行矩阵求逆运算,有时会出现奇异现象,导致计算失败。
本文根据以上缺点进行如下改进:(1) 应用极大似然估计法简化拉格朗日优化函数,使计算拉格朗日乘子不再具有高度非线性;(2) 提出了逐次优化法代替拟牛顿法,避免了初始点选择的影响且提高了计算精度;(3) 重新推导了线性变换公式避免了矩阵求逆运算,使优化算法更加稳健。
文中将拉格朗日乘子由非线性最小二乘法确定的最大熵概率密度估计称为经典型最大熵概率密度估计;将拉格朗日乘子由极大似然估计法确定的最大熵概率密度估计称为极大似然最大熵概率密度估计。
1 极大似然最大熵概率密度估计及其实现 1.1 经典型最大熵概率密度估计| $ S = - \int\limits_R {f\left( x \right)\ln \left[ {f\left( x \right)} \right]{\rm{d}}x} $ | (1) |
最大熵的基本方程为
| $ \begin{array}{l} {\rm{Max}}\;S = - \int\limits_R {f\left( x \right)\ln \left[ {f\left( x \right)} \right]{\rm{d}}x} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\int\limits_R {f\left( x \right){\rm{d}}x = 1} \\ \;\;\;\;\;\;\;\;\int\limits_R {{x^i}f\left( x \right){\rm{d}}x = {m_i}\;\;} i = 1,2, \cdots ,n \end{array} $ | (2) |
式中:f(x) 为变量X的理论概率密度函数;R为变量X的变化范围;mi为第i阶原点矩,其数值由样本确定。
| $ f\left( x \right) = \exp \left( { - \sum\limits_{i = 0}^n {{\lambda _i}{x^i}} } \right) $ | (3) |
| $ {\lambda _0} = \ln \int_R {\exp \left( { - \sum\limits_{i = 0}^n {{\lambda _i}{x^i}} } \right){\rm{d}}x} $ | (4) |
式中λ0, λ1, …, λi为拉格朗日乘子,由残差余量ei的平方和最小确定,即
| $ {\rm{Min}}\;{e^2} = \sum\limits_{i = 1}^n {e_i^2} $ | (5) |
| $ {e_i} = 1 - \frac{{\int_R {{x^i}\exp \left( { - \sum\limits_{j = 0}^n {{\lambda _j}{x^j}} } \right){\rm{d}}x} }}{{{m_i}\int_R {\exp \left( { - \sum\limits_{j = 0}^n {{\lambda _j}{x^j}} } \right){\rm{d}}x} }}\;\;i = 1,2, \cdots ,n $ | (6) |
目前国内外文献普遍采用拟牛顿法求解式 (5)。但由于拟牛顿法的局限性,在确定拉格朗日乘子时遇到如下问题:(1) 寻优结果对初始点的选择较敏感,若选取不合理,寻优结果不理想;(2) 优化函数的高度非线性使拟牛顿法寻优效率下降,往往造成寻优结果不收敛。
1.2 极大似然最大熵概率密度估计极大似然估计法是一种综合总体概率密度函数和样本信息,求解总体概率分布模型中未知参数的方法。其原理是基于总体概率密度函数构造一个包含未知参数的似然函数,求解似然函数最大时的未知参数,由此得到的概率分布模型与样本数据拟合性最好。
设变量X是一个连续随机变量,其概率密度函数f(x) 可表示为最大熵概率密度函数式 (3)。样本观测系列x1, x2, …, xl为递增离散系列 (x1≤x2≤…≤xl),则样本的似然函数为
| $ L\left( {{\lambda _0},{\lambda _1}, \cdots ,{\lambda _n}} \right) = \prod\limits_{j = 1}^l {\exp \left( { - \sum\limits_{i = 0}^n {{\lambda _i}x_j^i} } \right)} $ | (7) |
为了使样本似然函数值L(λ0, λ1, …, λn) 不随子样个数增加而增加,样本似然函数可写为如下形式
| $ L'\left( {{\lambda _0},{\lambda _1}, \cdots ,{\lambda _n}} \right) = {\left( {\prod\limits_{j = 1}^l {\exp \left( { - \sum\limits_{i = 0}^n {{\lambda _i}x_j^i} } \right)} } \right)^{\frac{1}{l}}} $ | (8) |
似然函数的对数为
| $ \begin{array}{*{20}{c}} {\ln L'\left( {{\lambda _0},{\lambda _1}, \cdots ,{\lambda _n}} \right) = \frac{1}{l}\sum\limits_{j = 1}^l {\left( { - \sum\limits_{i = 0}^n {{\lambda _i}x_j^i} } \right)} = }\\ { - \sum\limits_{i = 0}^n {{\lambda _i}\left( {\frac{1}{l}\sum\limits_{j = 0}^l {x_j^i} } \right) = - \sum\limits_{i = 0}^n {{\lambda _i}{m_i}} } } \end{array} $ | (9) |
式中:mi为样本的第i阶原点矩,m0=1。
利用极大似然原理,以拉格朗日乘子为优化变量,lnL′(λ0, λ1, …, λn) 最大值为优化目标,即可确定出最大熵概率密度函数。比较优化公式 (6,9),可以看出极大似然最大熵概率密度估计的优化函数不再具有高度非线性。
1.3 极大似然最大熵概率密度估计的优化算法及计算机实现为了进一步解决经典型最大熵、极大似然最大熵概率密度估计 (式 (6,9)) 优化过程中寻优拉格朗日乘子的初始点问题,即优化结果不理想、求解效率低或计算不收敛等问题,本文采用逐次优化法来求解拉格朗日乘子。
由于各阶样本原点矩mi不相关[5],所以本文的逐次优化法在寻优拉格朗日乘子时,优化函数从低阶到高价逐次加入原点矩,并更新最大熵概率密度公式。
下面以极大似然最大熵概率密度公式的计算实现为例,来阐述本文提出的逐次优化步骤。设拉格朗日乘子的个数为M,n=1, 2, …, M-1,则有:
(1) 当n=1,设优化变量为V1=[λ1],V1=[0]为初始值,令
(2) n=2,设优化变量为V2=[λ1 λ2],V2=[λ1*(1)0]为初始值,令
(3) 增加n值,如此往复,直至n=M-1,求得最终的最优变量Vn*,并由
(4) 由最终的拉格朗日乘子代入式 (3),即可得到最大熵概率密度公式。
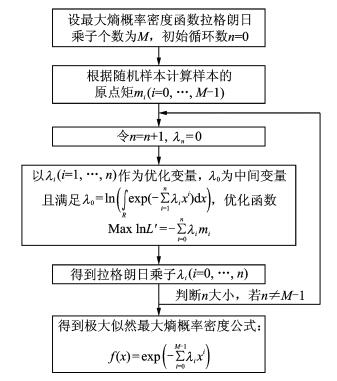
极大似然最大熵概率密度估计+逐次优化法的求解框图详见图 1。
|
图 1 极大似然最大熵概率密度估计+逐次优化计算框图 Figure 1 Diagram of MLE maximum entropy probability density estimation with sequential optimization method |
1.4 积分区间变换
利用极大似然最大熵概率密度估计+逐次优化法寻优拉格朗日乘子时,需计算
为此,文献[6]提出将x的积分区间线性变换到[0, 1],求出变换后的拉格朗日系数λ′,由变换前后拉格朗日乘子的关系H·λ=λ′,计算变换前的拉格朗日系数λ,确定原问题的最大熵概率密度函数。
由关系式H·λ=λ′确定变换前的拉格朗日系数时,需对变换矩阵H求逆,但变换矩阵H求逆有时会出现奇异现象,导致结果不正确。为避免这种情况,本文重新推导线性变换前后拉格朗日乘子的关系λ=G·λ′,推导内容如下:
设原问题的积分区间为l≤x≤u,线性变换为l′≤x′≤u′,则这两个积分区间表示的概率密度函数定义如下
| $ l \le x \le u\;\;\;\;{f_1}\left( x \right) = \exp \left( { - \sum\limits_{i = 0}^n {{\lambda _i}x_j^i} } \right) $ | (10) |
| $ l' \le x' \le u'\;\;\;\;{f_2}\left( {x'} \right) = \exp \left( { - \sum\limits_{i = 0}^n {{{\lambda '}_i}{{\left( {x'} \right)}^i}} } \right) $ | (11) |
令
| $ S = \frac{{u' - l'}}{{u - l}} $ | (12) |
| $ A = \frac{{Sl - l'}}{S} $ | (13) |
则
| $ x = \frac{{x' - l'}}{S} + l = A + \frac{{x'}}{S} $ | (14) |
根据概率论知识可知
| $ {f_1}\left( x \right) = S{f_2}\left( {x'} \right) $ | (15) |
将式 (15) 代入式 (11) 可得
| $ \frac{1}{S}{f_1}\left( x \right) = \exp \left\{ { - \sum\limits_{i = 0}^n {\left[ {{{\lambda '}_i}{{\left[ {S\left( {x - A} \right)} \right]}^i}} \right]} } \right\} $ | (16) |
化简式 (16) 可得
| $ \begin{array}{*{20}{c}} {{f_1}\left( x \right) = \exp \left\{ {\ln S - \sum\limits_{i = 0}^n {\left[ {{{\lambda '}_i}{S^i}{{\left( { - A} \right)}^i}} \right]} - } \right.}\\ {\left. {\sum\limits_{i = 1}^n {\left[ {{{\lambda '}_i}{S^i}\sum\limits_j^i {C_i^j{x^j}{{\left( { - A} \right)}^{i - j}}} } \right]} } \right\}} \end{array} $ | (17) |
将式 (10,17) 进行对比可得
| $ {\mathit{\boldsymbol{\lambda }}^{\rm{T}}} = \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\lambda '}}}^{\rm{T}}} $ | (18) |
式中
| $ \begin{array}{l} \mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} {C_0^0{S^0}{{\left( { - A} \right)}^0}}&{C_1^0{S^1}{{\left( { - A} \right)}^1}}&{C_2^0{S^2}{{\left( { - A} \right)}^2}}& \cdots &{C_{n - 1}^0{S^{n - 1}}{{\left( { - A} \right)}^{n - 1}}}&{C_n^0{S^n}{{\left( { - A} \right)}^n}}\\ 0&{C_1^1{S^1}{{\left( { - A} \right)}^0}}&{C_2^1{S^2}{{\left( { - A} \right)}^1}}& \cdots &{C_{n - 1}^1{S^{n - 1}}{{\left( { - A} \right)}^{n - 2}}}&{C_n^1{S^n}{{\left( { - A} \right)}^{n - 1}}}\\ 0&0&{C_2^2{S^2}{{\left( { - A} \right)}^0}}& \cdots &{C_{n - 1}^2{S^{n - 1}}{{\left( { - A} \right)}^{n - 3}}}&{C_n^2{S^n}{{\left( { - A} \right)}^{n - 2}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&0&0&0&{C_{n - 1}^{n - 1}{S^{n - 1}}{{\left( { - A} \right)}^0}}&{C_n^{n - 1}{S^n}{{\left( { - A} \right)}^1}}\\ 0&0&0&0&0&{C_n^n{S^n}{{\left( { - A} \right)}^0}} \end{array}} \right]\\ \;\;\;\;\;\mathit{\boldsymbol{\lambda '}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{{\lambda '}_0}}&{{{\lambda '}_1}}&{{{\lambda '}_2}}& \cdots &{{{\lambda '}_{n - 1}}}&{{{\lambda '}_n}} \end{array}} \right]\;\;\;\;\;\;\;\mathit{\boldsymbol{\lambda = }}\left[ {\begin{array}{*{20}{c}} {{\lambda _0} + \ln S}&{{\lambda _1}}&{{\lambda _2}}& \cdots &{{\lambda _{n - 1}}}&{{\lambda _n}} \end{array}} \right] \end{array} $ |
利用式 (18) 即可避免变换矩阵的求逆运算,克服计算溢出现象。至此极大似然最大熵概率密度估计步骤如下:
(1) 将随机子样数据进行线性变换成x′;
(2) 设拉格朗日乘子个数为M,求出x′的M-1阶原点矩mi(i=1, 2, …, M-1);
(3) 运用极大似然最大熵概率密度估计+逐次寻优方法计算线性变换后的拉格朗日乘子[λ′0, λ′1, …, λ′n];
(4) 由式 (18) 求出线性变换前的拉格朗日乘子[λ0, λ1, …, λn];
(5) 由式 (3) 得到原问题的极大似然最大熵概率密度公式。
2 算例分析与讨论 2.1 极大似然最大熵概率密度估计法对常见概率分布类型的计算分析通过4种常见的分布类型 (威布尔分布,对数正态分布,正态分布,Gamma分布) 验证极大似然最大熵概率估计法的通用性。
利用MonteCarlo方法生成1 000个随机样本,样本分别服从威布尔分布W(10, 5, 8)(形状参数为10,位置参数为5,尺度参数为8), 对数正态分布LogN(4, 0.5)(对数期望为4,对数标准差为0.5),正态分布N(20, 1) (期望为20,标准差为1), Gamma分布G(3, 4)(形状参数为3,尺度参数为4)。
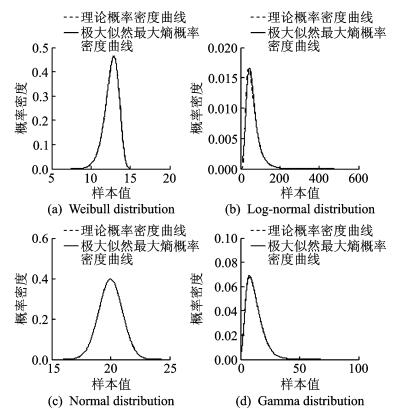
基于随机样本的前6阶原点矩,应用极大似然最大熵概率密度估计法+逐次优化法寻优拉格朗日乘子,获得极大似然最大熵概率密度函数。极大似然最大熵概率密度曲线与理论概率密度曲线对比见图 2。
|
图 2 4种常见概率分布类型的极大似然最大熵概率密度曲线与理论概率密度曲线对比 Figure 2 Comparison of four common probability distribution between theoretical and MLE maximum entropy PDF curves |
图 2显示在大样本情况下针对常见的概率分布类型,极大似然最大熵概率密度函数曲线与理论概率密度曲线十分吻合,表明极大似然最大熵概率估计法+逐次优化法较强的通用性及概率密度函数公式的统一性 (即服从不同分布类型的随机变量可由不同拉格朗日乘子的最大熵概率密度函数表示)。
2.2 极大似然最大熵与经典型最大熵概率密度估计法计算精度对比利用MonteCarlo方法生成1 000个随机样本,样本分别服从对数正态分布LogN(4, 0.5)(对数期望为4,对数标准差为0. 5),威布尔分布W(10, 5, 8)(形状参数为10,位置参数为5,尺度参数为8);其他分布类型具有相似的结论,在此不一一阐述。
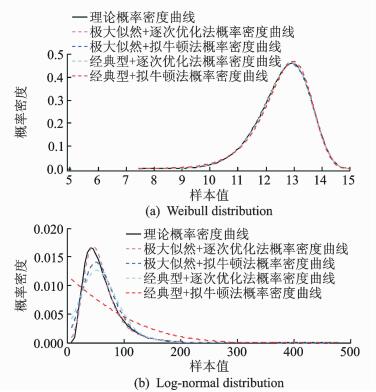
基于随机样本前6阶原点矩,将极大似然最大熵概率密度估计法、经典型最大熵概率密度估计法分别与拟牛顿法、逐次优化法组合,计算随机变量的概率密度函数。表 1列出不同方法组合计算的概率密度函数均方根误差,图 3显示基于不同方法组合的概率密度曲线与理论概率密度曲线的对比。
均方根误差的计算公式如下
| 表 1 不同方法组合产生的概率密度函数均方根误差 Table 1 RMSE of probability density function caused by different method combinations |
|
图 3 不同方法组合的概率密度曲线对比 Figure 3 Comparison among probability density curves based on different method combinations |
| $ {\rm{RMSE = }}\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {\frac{{{{\hat x}_i} - {x_i}}}{{{x_i}}}} \right)}^2}} } $ | (19) |
式中:
表 1和图 3结果表明:对于相同的最大熵概率密度估计方法,逐次优化法计算精度优于拟牛顿法。对于相同的优化方法,极大似然最大熵概率密度估计法优于经典型最大熵概率密度估计法。方法组合的计算精度从高到低的排列顺序为:极大似然+逐次优化法、极大似然+拟牛顿法、经典型+逐次优化法、经典型+拟牛顿法。
变量服从威布尔分布时,4种方法组合计算的概率密度曲线与理论概率密度曲线吻合较好。但当变量服从对数正态分布时,图 3可以明显看出不同方法组合计算的概率密度曲线偏离理论概率密度曲线的误差各不相同。分析其原因如下:(1) 经典型+拟牛顿法计算精度最差。由于拟牛顿法的局限性同时拉格朗日优化函数的高度非线性,计算精度对于初始点的选择较敏感,文中由于初始点选择不合理,导致优化结果不收敛。(2) 逐次优化法克服了拟牛顿
法受初始点选择的影响,避免优化结果不收敛,使经典型+逐次优化法较经典型+拟牛顿法具有更高的计算精度。(3) 极大似然估计法简化了拉格朗日优化函数,寻优过程不再高度非线性,较经典型估计法更易获得优化函数的最优解。
2.3 最大熵概率密度估计法在可靠性问题中的应用在工程实践中,研究对象的属性 (如结构疲劳寿命,应力强度) 一般具有分散性,工程设计中将其视为随机变量。利用最大熵概率密度估计法可方便地计算出给定属性值对应的可靠度。基于最大熵概率密度估计法的可靠度公式为
| $ R\left( t \right) = 1 - \int_{ - \infty }^t {\exp \left( { - \sum\limits_{i = 0}^n {{\lambda _i}{x^i}} } \right){\rm{d}}x} $ | (20) |
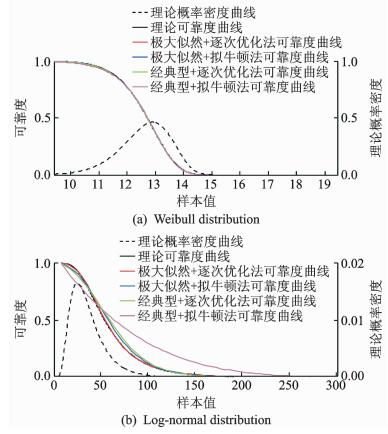
利用MonteCarlo方法生成1 000个随机样本,样本分别服从威布尔分布W(10, 5, 8)(形状参数为10,位置参数为5,尺度参数为8),对数正态分布LogN(4, 0.5)(对数期望为4,对数标准差为0.5)。其他分布类型,如正态分布,Gamma分布得到的结论相似,在此不一一阐述。基于样本的前6阶原点矩,应用最大熵概率密度估计法计算随机变量的可靠度函数。图 4显示了不同方法组合计算的可靠度函数曲线与理论可靠度函数曲线的对比。表 2列出了不同方法组合计算的可靠度函数均方根误差,均方根误差公式见式 (19)。
|
图 4 不同方法组合的可靠度曲线对比 Figure 4 Comparison of reliability curves among different method combinations |
| 表 2 不同方法组合的可靠度估计均方根误差 Table 2 RMSE of reliability estimation based on different method combinations |
图 4和表 2结果表明,基于最大熵概率密度函数可方便求出随机变量的可靠度函数。组合方法的计算精度对比与2.2节结论一致,即极大似然最大熵概率密度估计法优于经典型最大熵概率密度估计法,逐次优化法优于拟牛顿法。4种方法组合中极大似然+逐次优化法的计算精度最高。
图 4显示4种方法组合计算威布尔分布的可靠度函数曲线与理论可靠度函数曲线较为吻合。但计算对数正态分布时,经典型+拟牛顿法由于初始点选择不合理及优化函数高度非线性,使计算的可靠度曲线与理论可靠度曲线偏离较远。
3 结论(1) 基于最大似然原理推导了拉格朗日优化函数的简化形式,提出了最大似然概率密度估计法。相比经典最大熵概率密度估计法,最大熵概率密度估计法优化函数表达式简单,非线性程度低,计算精度更高。
(2) 本文提出的逐次优化法将高维拉格朗日优化问题转化为一系列低维拉格朗日优化问题。在取得低维优化问题最优解的基础上,逐次增加拉格朗日乘子数目,有效地避开初始点选择问题,与拟牛顿法相比,优化过程更易收敛,计算精度更高。
(3) 针对求解拉格朗日乘子时变换矩阵求逆导致的奇异现象,本文重新推导了线性变换前后拉格朗日乘子的关系式,避免矩阵求逆运算,提高寻优过程中的稳定性。
(4) 算例结果对比表明:4组方法组合中,极大似然最大熵+逐次优化法计算精度最高,稳定性最好。
| [1] | SINGH P V, ZHANG L, RAHIMI A. Probability distribution of rainfall-runoff using entropy theory[J]. Transactions of the ASABE, 2012, 55(5): 1733–1744. DOI:10.13031/2013.42364 |
| [2] | ZHANG L, XIA X, WANG Z.Maximum entropy bootstrap method for parameter estimation[C]//Seventh International Symposium on Instrumentation and Co ntrol Technology:Measurement Theory and Systems and Aeronautical Equipment.Bellingham:SPIE-Int Soc Optical Engineering, 2008. |
| [3] | LI C Q, WANG W, WANG S. Maximum entropy Monte Carlo method for the evaluation of dam overtopping proba bility[J]. Disaster Advances, 2012, 5(4): 1143–1147. |
| [4] | RAMIREZ P, CARTA J A. The use of wind probability distributions derived from the maximum entropy principle in the analysis of wind energy[J]. Energy Conversion and Management, 2006, 47(15/16): 2564–2577. |
| [5] | WU X. Calculation of maximum entropy densities with application to income distribution[J]. Journal of Econometrics, 2003, 115(2): 347–354. DOI:10.1016/S0304-4076(03)00114-3 |
| [6] |
高翔, 郑建祥.
基于最大熵概念的复杂随机变量统计模型[J]. 农业机械学报, 2008, 38(2): 43–46.
GAO Xiang, ZHENG Jianxiang. Statistical distribution model of complicated random variables based on maximum entropy concept[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 38(2): 43–46. |
| [7] |
吕文.最大熵原理与贝叶斯方法在测量数据处理中的应用[D].成都:电子科技大学, 2006.
LV Wen.The applications of maximum entropy method and Bayes in data processing[D].Chengdu:University of Electronic Science and Technology of China, 2006. |
| [8] | BARDUCCI A, GUZZI D, LASTRI C, et al. Emissivity and temperature assessment using a maximum entropy estimator:Structure and performance of the maxentes algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 738–751. DOI:10.1109/TGRS.2014.2327218 |
| [9] | MOHTASHAMI B G R.Characterization of Pearsonian and bilateral power series distribution via maximum entropies[C]//Bayesian Inference and Maximum Entropy Methods in Science and Engineering.Gif-Sur-Yvette, France:American Institute of Physics, 2001. |
| [10] | ZHANG H, JING Y Y, LIU Z Y. Study on the maximum entropy principle applied to the annual wind speed probability distribution:A case study for observations of intertidal zone anemometer towers of Rudong in east China sea[J]. Applied Energy, 2014, 114: 931–938. DOI:10.1016/j.apenergy.2013.07.040 |
| [11] | ZHANG J, TEIXEIRA A P, SHI X H. Structural reliability analysis based on probabilistic response modelling using the maximum entropy method[J]. Engineering Structures, 2014, 70: 106–116. DOI:10.1016/j.engstruct.2014.03.033 |
| [12] | MARCO B. A maximum entropy approach to loss distribution analysis[J]. Entropy, 2013, 15(3): 1100–1117. DOI:10.3390/e15031100 |
| [13] | LYNN K R, REZA M A.Maximum entropy estimation of the probability density function from the histogram using order statistic constraints[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing.New York:IEEE, 2013. |
| [14] | BRETTHORST G L. The maximum entropy method of moments and Bayesian probability theory[J]. Bayesian Inference and Maximum Entropy Methods in S cience and Engineering, 2013, 1553: 3–15. |
| [15] | OLIVARES S, MATTEO G A. About the probability distribution of a quantity with given mean and variance[J]. Metrologia, 2012, 49(3). |
| [16] | ZHU Hehua, ZUO Yulong, LI Xiaojun, et al. Estimation of the fracture diameter distributions using the maximum entropy principle[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 72: 127–137. DOI:10.1016/j.ijrmms.2014.09.006 |
| [17] | YU L J, ZHANG X N.Maximum entropy models for mode split forecasting[C]//IEEE/Informs International Conference on Service Operations, Logistics and Informatics.New York:IEEE, 2009:609-613. |
| [18] | DENG J, PANDEY M D, XIE W C.Maximum entropy principle and partial probability weighted moments[C]//American Institute of Physics Conference.Melville:American Inst Physics, 2012:190-197. |
| [19] |
李填, 夏良正, 顾宗悫.
一种新的二维最大熵图象阈值分割方法[J]. 南京航空航天大学学报, 1994(S1): 151–157.
LI Zhen, XIA Liangzheng, GU Zongque. A new method of image thresholding segmentation using two-dimensional maximum entropy[J]. Journal of Nanjing University o f Aeronautics & Astronautics, 1994(S1): 151–157. |
 2017, Vol. 49
2017, Vol. 49


