发动机试车台地面模拟试验是发动机研制系统工程重要组成部分,目的在于确定发动机性能指标,评价发动机可靠性和寿命,不断完善和发展发动机理论研究。目前传统单分量测力方法己不能满足科学技术发展要求。在发动机推力测试中,采用单一主推力测试方法不可能取得发动机工作特性的准确数据。只有通过测量寄生分量(两个侧向力和3个力矩)和轴向载荷,以及它们与各个测量量的关系,才能取得发动机工作特性的准确数据。这些问题只有通过矢量推力测量才能解决。随着现代航空航天工业的迅速发展, 发动机推力矢量测量,特别是推力矢量随机测量的功能越来越成为发动机发展的一个重要方面[1]。
1 现阶段试车台校准存在的问题目前高空发动机试车台矢量推力测量系统的校准主要在实验室开展,即将测力传感器拆卸送到实验室进行校准。但在实际使用过程中,由于台架安装精度要求动架体上端、动架体下端和主推力承力架的同轴度不大于0.1 mm,反复拆装传感器耽误时间,且容易使测量条件由于安装而产生变化,导致测量数据的不准确。另外试车时推力为动态的力,测力传感器在静态下计量而使用在动态环境中,测力传感器所测量的数值与实际推力数值有很大的区别,实际现场使用时误差增至±5%~±10%的情况也不少见,造成了发动机试车台推力的测量不准确,进而对发动机的工作时间,导弹的飞行速度、射程产生重要影响。
对于引起误差的原因,主要是由于校准条件和使用条件不同,包括以下几方面[2-5]:
(1) 目前的高空发动机试车台推力校准方法为采用标准力传感器通过挠性杆组件连接工作级传感器,两类传感器同步感知推力信号,以标准力传感器测得力值信号为激励,工作级传感器的输出为响应,求取推力传感器的工作模型,其中标准力传感器往往采取单独标定的方法溯源至上一级标准。实际使用时,当溯源后的标准力传感器安装在发动机推力台架上,其等效刚度不可避免发生变化,此时标准力传感器标定的灵敏度将随之发生偏移,最终降低静态校准的精度;
(2) 力传感器校准环节中,力传感器需牢靠固定于发动机推力台上,由理论推导和测试数据可知,推力台低频模态比较丰富,当力传感器与推力台形成一体后,力传感器感知推力信号在其频域范围内激发多阶低频模态,力传感器在其工作频域形成多个共振峰,导致力传感器频响函数在低频工作范围内不再是平坦直线,极大地影响了校准精度,因此需要开展动态校准及其补偿方法的研究;
(3) 高空发动机试车台推力台架上共安装8只测力传感器,共同求取发动机矢量力,依据矢量推力计算模型可知,矢量力的精确求取,取决于测力传感器测得的空间矢量的严格同步,当各路空间矢量之间存在时延(频率域表现为各路信号存在相位偏差),则对应各个时刻点上的矢量计算结果将会出现偏差,因此各路测试信号相位的一致性对于推力矢量的准确计算至关重要。在实际工作中,由于各路空间矢量测试系统的不一致性,空间矢量相位偏差不可避免,推力矢量计算精度受到影响,因此有必要针对校准的动态特性曲线进行相位补偿方法研究,以便确保各路信号的相位一致性。
综上,随着研制任务的深入开展,对矢量推力试验台测量精度要求越来越高,而矢量推力试验台尚未开展矢量推力现场校准工作。为降低实验室校准与实际使用条件不同而产生的附加误差,提高矢量推力测量系统的精度,迫切需要开展矢量推力试验台现场推力校准方法研究。
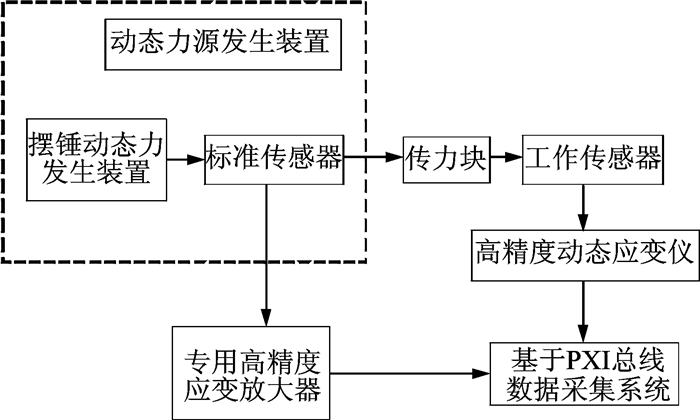
2 高空发动机试车台矢量推力现场动态校准的设计 2.1 矢量推力校准方案通过对现阶段不同动态力发生装置的比较[6-8],本文采取摆锤式动态力发生装置完成推力测量系统动态校准任务。其工作原理如图 1所示,校准时将摆锤提升到一定角度,并采用特定机构固定摆锤,当校准系统准备完毕后,释放摆锤,对于垂直于地面安装主推力传感器而言,摆锤下落至水平位置击中传力块,传力块将力值传递至推力传感器,对于其余水平安装推力传感器而言,摆锤则是下落至垂直位置击中传力块,传力块将力值传递至推力传感器。通过调整系统参数,如摆锤质量、提升角度等可获得不同脉宽及幅值的力值信号。
|
图 1 原位现场校准总体框图 Figure 1 General scheme of field calibration |
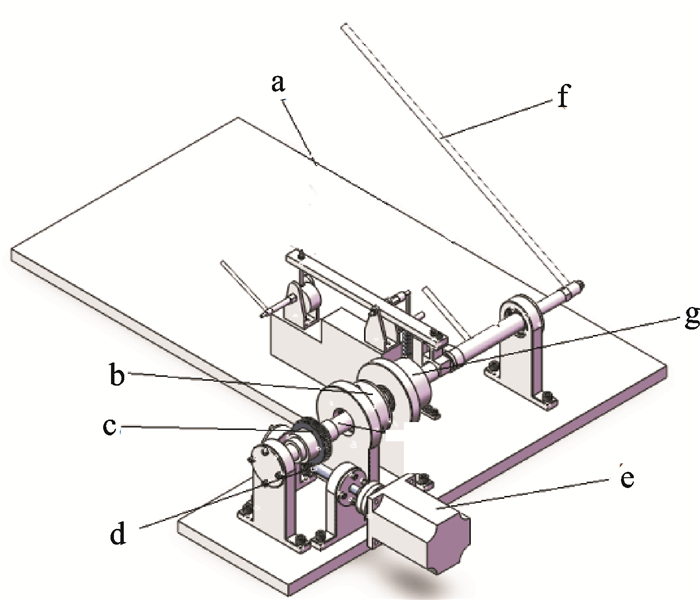
图 2为摆锤式动态力发生装置总体结构示意图。机械部分主要包括:a.底座、b.电磁离合器、c.蜗轮、d.蜗杆、e.步进电机、f.旋转编码器、g.摆杆。
|
图 2 校准装置机械结构示意图 Figure 2 Machine construction of pendulum bob calibration system |
控制系统控制电磁离合器闭合,并控制步进电机转动,通过蜗杆蜗轮减速装置带动摆锤提升,摆锤提升角度由旋转编码器获得。当摆锤提升到设定角度后,步进电机停止转动。由于蜗轮蜗杆减速装置具有自锁作用,在无电机驱动扭矩的作用下,摆锤不会自由下落。当需要摆锤自由下落时,控制系统控制电磁离合器分离,摆锤将在重力作用下自由下落并撞击传力块,进而将力值传递给被校推力传感器。撞击后摆锤将反弹,通过控制系统自动控制电磁离合器闭合,并结合蜗轮蜗杆的自锁作用,可以固定摆锤,防止二次撞击。校准装置的摆杆长度设计为可调,同时防二次撞击机构中的凸轮滑杆长度和滑块弹簧的压缩量均设计为可调。
2.2 矢量推力数据的处理通常利用最小二乘法对数据进行线性平滑法数据处理[9],五点滑动平均的计算公式为
| $ \begin{array}{l} \left. \begin{array}{l} {y_1}{\rm{ = }}\frac{1}{5}\left( {3{x_1} + 2{x_2} + {x_3} - {x_4}} \right)\\ {y_2} = \frac{1}{{10}}\left( {4{x_1} + 3{x_2} + 2{x_3} + {x_4}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {y_i} = \frac{1}{5}\left( {{x_i} - 2 + {x_i} - 1 + {x_{i + 1}} + {x_{i + 2}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {y_{m - 1}} = \frac{1}{{10}}\left( {{x_{m - 3}} + 2{x_{m - 2}} + 3{x_{m - 1}} + 4{x_m}} \right)\\ {y_m} = \frac{1}{5}\left( { - {x_{m - 3}} + {x_{m - 2}} + 2{x_{m - 1}} + 3{x_m}} \right) \end{array} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {i = 3, 4, \cdots , m - 2} \right) \end{array} $ | (1) |
而五点平滑法滤波相当于一个低通滤波器,将高频噪声成分滤去。
动态特性指测试系统对随时间变化的输入信号的输出响应特性。主推力方向上的响应曲线表明系统可看为一个二阶(或二阶以上)系统,所以从二阶系统方面入手对系统进行分析,求出其动态性能指标,至于二阶以上系统,可以将其看成二阶系统与其他低阶系统的组合。二阶系统动态特性指标可分为时域和频域两种,时域指标的特征量主要包括减幅系数α,阻尼比ζ,超调量σ,衰减率d,延迟时间td,上升时间tτ,峰值时间tp和响应时间ts等。频域指标中应用最广泛的是固有频率fn,系统的传递函数,通频带fb等(幅值衰减为0.707倍处的频率)。
上升时间、振荡周期和谐振频率等可以由响应曲线读取,减幅系数为
| $ \alpha = \frac{1}{T}\ln \frac{{{A_1}}}{{{A_2}}} $ | (2) |
阻尼比为
| $ \zeta = \frac{a}{{{\omega _n}}} = \frac{1}{T}\ln \frac{{{A_1}}}{{{A_2}}}l{\omega _n} $ | (3) |
固有频率为
| $ {f_n} = \frac{{{f_x}}}{{\sqrt {1 - 2{\zeta ^2}} }} $ | (4) |
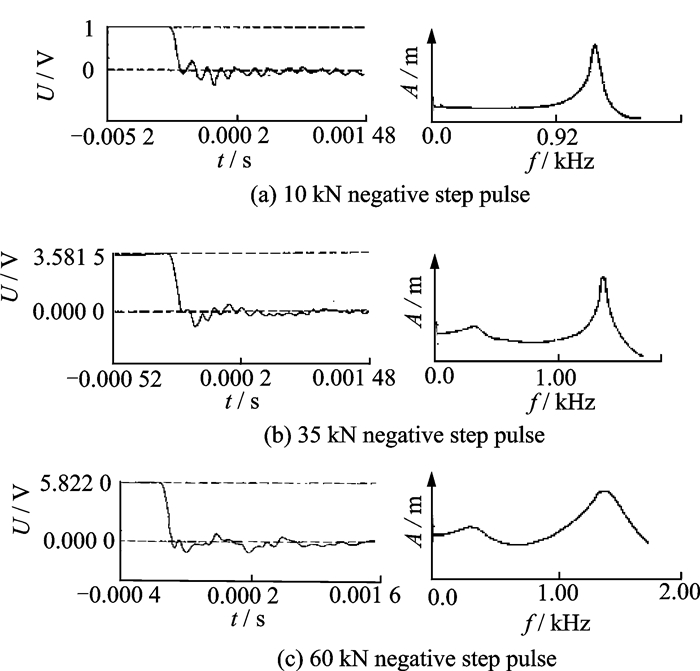
图 3给出了某测力传感器分别经受10,35,60 kN负阶跃力输出响应及对应幅值谱曲线。
|
图 3 力传感器在不同量值阶跃作用下的响应谱 Figure 3 Response and amplitude spectrum by trust sensor with step force |
2.3 矢量推力校准系统的溯源
本文中的发动机试车台矢量推力校准系统应充分考虑到溯源性,其动态力校准的溯源图如图 4所示[10]。

|
图 4 校准设备溯源图 Figure 4 Traceability figure of calibration system |
3 发动机试车台矢量推力现场动态校准不确定度预估
(1) 测量不确定度的A类评定
系统的测量重复性是在试验过程中获得的独立重复测量数据,根据该测量数据利用贝塞尔公式计算实验标准差,该实验标准差即为重复性,该部分重复性主要由传感器测量力值时引入。A类测量不确定度为:uA=2.0×10-3。
(2) 测量不确定度的B类评定
该项不确定度主要由工作传感器的不确定度、传感器及挠性杆组合件位置误差不确定、调理电路相对不确定、数采系统不确定、动架轴线与校准坐标的不同轴性引起的误差和随机干扰噪声不确定引入不确定度[11-12]组成。
① 工作传感器引入组成的不确定度分量,按均匀分布估计,u1=2.0×10-3。
② 传感器及挠性杆组合件位置误差引入的测量不确定度分量,按均匀分布估计:u2=3.0×10-2。
③ 调理电路引入的测量不确定度分量,按均匀分布估计:u3=1.0×10-3。
④ 数采系统引入的测量不确定度分量,按正态估计:u4=1.0×10-3。
⑤ 随机干扰噪声引入的测量不确定度分量,按正态分布估计:u5=3.0×10-3。
⑥ 动架轴线与校准坐标的不同轴性引入的测量不确定度分量按正态分布估计:u6=5.0×10-3。
⑦ 标准动态力传感器引入测量不确定度分量,按均匀分布估计:u7=5.0×10-3。
⑧ 动态加载装置稳定度引入的测量不确定度分量按正态分布估计:u8=4.0×10-3。
⑨ 动态加载装置波形失真引入的测量不确定度分量按正态分布估计:u9=5.0×10-3。
测量不确定度合成为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{u_c} = \sqrt {\sum\limits_{i = 1}^n {u_{{{\rm{A}}_i}}^2} + \sum\limits_{j = 1}^m {u_{{{\rm{B}}_j}}^2} } = \\ \sqrt {u_A^2 + u_1^2 + u_2^2 + u_3^2 + u_4^2 + u_5^2 + u_6^2 + u_7^2 + u_8^2 + u_9^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1.1\% \end{array} $ |
矢量推力动态校准扩展不确定度为
| $ {U_{{\rm{rel}}}} = k{u_c} = 2 \times 1.1\% = 2.2\% , \;k = 2 $ |
不确定度汇总如表 1所示。
| 表 1 不确定度汇总表 Table 1 Summary sheet of uncertainty components |
4 结束语
本文根据发动机试车台校准需求,提出了一种利用摆锤式动态力加载装置实现高空发动机试车台矢量推力现场动态校准方法,校准时将摆锤提升到一定角度,并采用特定机构固定摆锤,当校准系统准备完毕后,释放摆锤。该方法结构简单,加载力源移动方便,可以很灵活地应用在试车台现场。通过试验表明,该方案; 动态性能优异, 响应迅速, ,动态校准不确定度2.2%,满足高空发动机试车台矢量推力测试的需求,为后续进一步准确测试矢量推力提供了依据。
| [1] |
黄知涛, 胡正峰, 郭伟民.
微型涡喷发动机地面试车台推力测量系统[J]. 测控技术, 1999(9): 40–42.
DOI:10.3969/j.issn.1000-8829.1999.09.014 HUANG Zhitao, HU Zhengfeng, GUO Weimin. The thust measurement system of the ground test bed of the micro-turboject engine[J]. Measurement & Control Technology, 1999(9): 40–42. DOI:10.3969/j.issn.1000-8829.1999.09.014 |
| [2] |
SAE-AIR4951. Test Cell Thrust Measurement[S].SAE, 2011. |
| [3] |
颜雄雄, 耿卫国.
小发动机推力矢量的测量[J]. 推进技术, 2000, 6(3): 86–88.
DOI:10.3321/j.issn:1001-4055.2000.03.025 YAN Xiongxiong, GENG Weiguo. Thrust vector measurement for small engine[J]. Journal of Propulsion Technology, 2000, 6(3): 86–88. DOI:10.3321/j.issn:1001-4055.2000.03.025 |
| [4] |
王红艳, 孙宝元, 钱敏, 等.
基于有限元分析的推力矢量测试平台研究[J]. 压电与声光, 2006, 28(5): 618–620.
DOI:10.3969/j.issn.1004-2474.2006.05.040 WANG Hongyan, SUN Baoyuan, QIAN Min, et al. Study on thrust vector measuring platform based on finite element method[J]. Piezoelectrics & Acoustooptics, 2006, 28(5): 618–620. DOI:10.3969/j.issn.1004-2474.2006.05.040 |
| [5] |
王洪业.
传感器工程[M]. 长沙: 国防科技大学出版社, 1997.
WANG Hongye. Sensor engines[M]. Changsha: National Defense Industry Press, 1997. |
| [6] |
何闻.
标准动态力发生装置国内外研究现状[J]. 机电工程, 1999(2): 47–49.
HE Wen. Summarization of standard dynamic force generator at home and abroad[J]. Journal of Mechanical & Electrical Engineering, 1999(2): 47–49. |
| [7] |
马晓利, 李永新.
基于加速度监测的落锤压力标定方法研究[J]. 计测技术, 2013, 33(4): 26–29.
DOI:10.3969/j.issn.1674-5795.2013.04.005 MA Xiaoli, LI Yongxin. Study of drop weight pressure gauge based on the acceleration monitoring[J]. Metrology & Measurement Technology, 2013, 33(4): 26–29. DOI:10.3969/j.issn.1674-5795.2013.04.005 |
| [8] |
张学成, 荆风林, 任敏, 等.
火箭发动机推力测量的原位自动校准[J]. 宇航计测技术, 1998, 18(2): 60–64.
ZHANG Xuecheng, JING Fenglin, REN Min, et al. Automatic calibration of rocket engine thrust measurement at the testing location[J]. Journal of Astronautic Metrology and Measurement, 1998, 18(2): 60–64. |
| [9] |
樊尚春, 占俊芳, 张庆荣, 等.
航空测试系统[M]. 北京: 北京航空航天大学出版社, 2005.
FAN Shangchun, ZHAN Junfang, ZHANG Qingrong, et al. Airborne measurement system[M]. Beijing: Beihang University Press, 2005. |
| [10] |
国家质量技术监督局.JJG632动态力传感器检定规程[S].北京: 中国质检出版社, 2011.
General Adminstration of Quality Supervision, Inspection and Quarantine of the People's Republic of China.JJG632 verification regulation of dynamic force sensors[S].Beijing: China Zhijian Publishing House, 2011. |
| [11] |
刘智敏.
不确定度原理[M]. 北京: 中国质检出版社, 1993.
LIU Zhimin. Principle of uncertainty in measurement[M]. Beijing: China Zhijian Publishing House, 1993. |
| [12] |
国家质量技术监督局.JJF 1059-1999测量不确定度评定与表示[S].北京: 中国质检出版社, 1999.
JJF 1059-1999Evaluation and Expression of Uncertainty in Measurement. Beijing: China Zhijian Publishing House, 1999. |
 2018, Vol. 50
2018, Vol. 50


