2. 中国空间技术研究院, 北京, 100094
2. Beijing Institute of Spacecraft System Engineering, Beijing, 100094, China
航天电子设备的可靠性在很大程度上取决于组成它的电子元器件的可靠性,而元器件的失效率是电子设备主要的可靠性指标[1], 失效率增加严重影响电子设备的寿命及系统任务的可靠性。随着电子元器件的高度集成,空间系统任务的可靠性对热环境要求愈发严格,尤其是当可靠性与温度相关时,组件故障强烈依赖于设备运行的温度[2]。
航天电子设备在空间应用中使用时,由于空间热环境造成的失效称为热失效。热失效是指由于过热或急剧温度变化而导致的烧毁、熔融、蒸发、迁移、断裂等失效。另外,许多材料长期处于低温环境时将变得冷脆,出现强度下降和脱落等现象[3]。文献[4]指出温度变化所产生的热应力也是电子元器件产品的主要失效因素。同样地在温度剧烈交变的环境中材料、组合部件会出现断裂、撕脱等损坏。
目前,研究电子元器件失效率对温度依赖性所使用的模型为文献[5]提出的Arrhenius指数模型,具体在计算失效率时引入环境因子进行修正,从而计算各种不同环境下的失效率,此种方法虽然一定程度上考虑了环境因素,但不同元器件在不同环境下的环境因子可能相差很大,计算实用性不强,对于各种典型元器件的失效率计算详细见文献[6]。而且目前研究大都没有考虑由于温度、形变剧烈变化对失效率的影响以及低温情况下的失效率计算。
本文采用基于模糊逻辑的智能算法研究了温度和应力大小对失效率的影响,以及温度和形变相对于上一时刻的变化对失效率的影响。本文研究为航天电子元器件的可靠性分析提供有效的失效率计算基础。
1 模糊逻辑模糊逻辑最早由Zadeh提出[7],用于处理不精确的或模糊的信息,是一种基于模糊集合论的数学方法。模糊集理论已经广泛应用于图像处理、语音识别、医疗诊断、证券交易和控制系统等领域。特别是模糊联想记忆系统和自适应模糊系统领域的发展,为机器学习和人工智能提供了重要的理论基础。
模糊逻辑和经典二值逻辑之间的根本区别在于集合的定义。经典集合论是基于二值逻辑的,即对象元素要么属于集合要么不属于集合,只有这两种状态。而在大多数情况下,命题的真实状态是既不完全正确,也不完全错误,而是模糊不精确的,不能确定地归属于某一明确清晰边界的集合,因此经典的二值逻辑使得它在现实世界的应用中是一个不恰当的推理过程。而模糊逻辑允许对象成为多个集合的成员[8],最重要的是它引入了隶属函数的概念,用来描述对象元素对模糊集合的隶属程度。
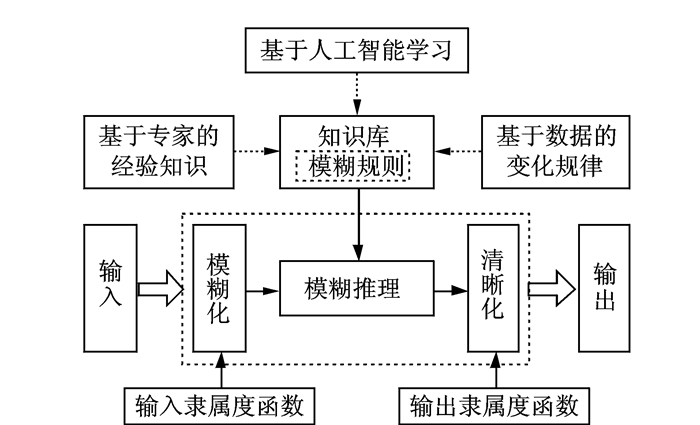
一般的模糊逻辑决策系统的结构如图 1所示。它由4部分组成,即模糊规则知识库,模糊推理过程,模糊化过程和去模糊化过程[9]。
|
图 1 典型模糊逻辑决策系统的结构 Figure 1 General structure of a typical fuzzy logic system |
图 1中,输入由模糊特征变量组成,输出由模糊的结论变量组成。系统的模糊化部分将清晰或模糊的输入值映射到预定义的模糊集。推理引擎在知识库中与输入数据匹配规则的前提,并执行模糊推理。将模糊的结论转化为清晰的数值。
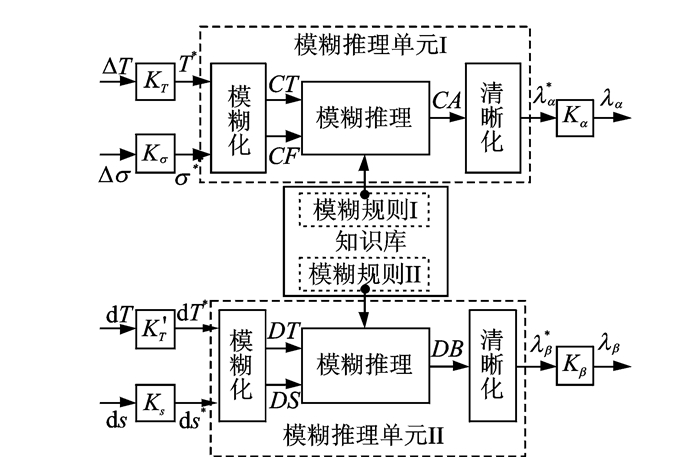
2 使用模糊逻辑进行失效率的分析失效率不仅与温度及应力的大小有关,而且还和温度及变形相对于上一时刻的变化率有关。本文采用两个模糊推理决策单元分别对此进行分析,整体的模糊推理决策系统如图 2所示。两个模糊推理单元所使用的模糊分割、标准化隶属度函数及模糊推理方法相同,但两者具体模糊化、清晰化过程中的论域尺度变换因子不同,模糊推理所使用的模糊规则不同。
|
图 2 模糊推理决策系统 Figure 2 Fuzzy logic inference decision units |
模糊推理单元Ⅰ分析温度及应力大小对失效率的影响。选择已知一定温度、应力条件下的失效率作为基准,输入到模糊推理单元Ⅰ的ΔT,Δσ是相对于基准温度、基准应力的偏移量,通过相应的模糊规则进行模糊推理得到相对基准失效率的偏移量,从而计算得出不同温度、应力条件下失效率的大小。模糊推理单元Ⅱ分析温度及形变相对于上一时刻的变化量对失效率的影响。输入到模糊推理单元Ⅱ的dT,ds是当前时刻相对于上一时刻温度、形变的相对变化量,通过相应的模糊规则进行模糊推理得到温度、形变不同变化率对失效率的影响。
2.1 模糊分割及隶属度函数模糊推理的输入和输出的语言变量分别构成了模糊输入空间和模糊输出空间。每个语言变量的取值为一组模糊语言名称,每个模糊语言名称相应一个模糊集合。对于每个语言变量,其取值的模糊集合具有相同的论域。模糊分割确定对于每个语言变量取值的模糊语言名称的个数。本文采用标准正则化论域[-3, 3],模糊集合及模糊语言见表 1,每一个模糊集合分为7个元素等级,模糊集合的下标代表语言值与哪个元素等级相关。
| 表 1 模糊集合及其模糊语言 Table 1 Fuzzy sets and fuzzy language |
隶属度函数选用铃型隶属函数
| $ \mu \left( x \right) = {{\rm{e}}^{ - \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{2{\sigma ^2}}}}} $ | (1) |
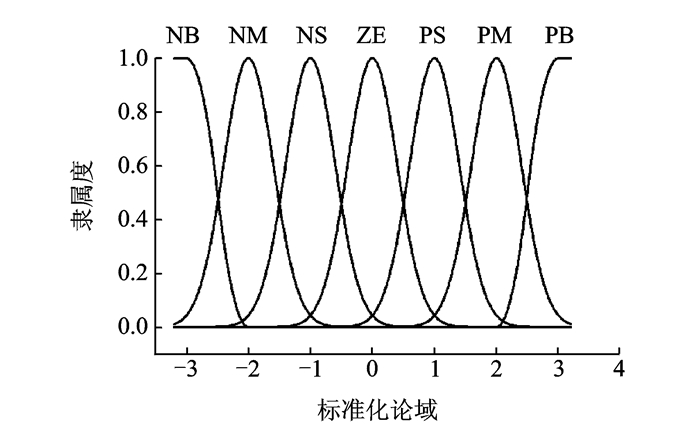
式中:x0为隶属度函数的中心值,σ2为方差,图 3为铃型隶属函数分布图。
|
图 3 隶属度函数 Figure 3 Membership functions |
2.2 模糊规则表的制定
本文通过经验知识及实验数据的变化规律制定两个模糊规则表, 分别实现温度及应力大小和温度变, 及形变相对于上一时刻变化对失效率的影响。
(1) 模糊规则表Ⅰ
反映温度对失效率最常用的是Jacobus提出的用于描述化学反应速度的Arrhenius方程
| $ f = A{e^{ - \frac{Q}{{kT}}}} $ | (2) |
式中:A为Arrhenius常数,一般取为2.356e+11, f为失效率,Q为活化能量(eV),一般取为0.674 eV,k为波尔兹曼常数(8.63×10-5 eV/K),T为温度(K)。方程表明,随着温度的升高,其失效率呈指数规律增长。另外,低温同样对失效率有很大的影响,温度越低失效率越高。而且温度引起的热应力也会引起机械损坏,导致元器件失效。模糊规则表见表 2。
| 表 2 模糊规则Ⅰ Table 2 Fuzzy rules Ⅰ |
(2) 模糊规则表Ⅱ
温度剧烈交变的环境中, 材料、组合部件会出现断裂、撕脱等损坏。由于温度梯度所产生的温度变化和热变形变化会导致疲劳失效。文献[1]指出,当元器件的温度循环变化超过±20 ℃时,其失效率可以增加到基本恒温时失效率的8倍以上。
形变变化相对较小的情况下,随着温度相对于上一时刻变化量越大,对失效率的影响越大;在温度变化一定的情况下,无论是拉伸形变还是压缩形变,相对变化量越大,对失效率的影响越大。模糊规则Ⅱ见表 3。
| 表 3 模糊规则Ⅱ Table 3 Fuzzy rules Ⅱ |
2.3 模糊推理计算
两个模糊推理单元进行模糊推理计算时,均需经过模糊化、模糊推理及清晰化3个基本过程,但是在模糊化及清晰化时论域之间的比例因子不同,在模糊推理所使用的模糊规则不同,说明如下:
(1) 模糊化
模糊化的作用是将输入量进行尺度变换,变换到各自的论域范围,然后将已变换到论域范围的输入量进行模糊处理,使原先精确的输入量变成模糊量,并用相应的模糊集合来表示。对于模糊推理单元Ⅰ,输入为
| $ \left\{ \begin{array}{l} {T^*} = {K_T}(\Delta T - \frac{{\Delta {T_{{\rm{max}}}} + \Delta {T_{{\rm{min}}}}}}{2})\\ {\sigma ^*} = {K_\sigma }(\Delta \sigma - \frac{{\Delta {\sigma _{{\rm{max}}}} + \Delta {\sigma _{{\rm{min}}}}}}{2}) \end{array} \right. $ | (3) |
式中:T*, σ*为变换到标准论域的输入量;ΔTmax, ΔTmin和Δσmax, Δσmin分别为实际输入所在研究范围的最大最小值;KT, Kσ分别为温度和应力输入变换的比例因子。
模糊推理单元Ⅱ,输入为
| $ \left\{ \begin{array}{l} {\rm{d}}{T^*} = {{K'}_T}({\rm{d}}T - \frac{{{\rm{d}}{T_{{\rm{max}}}} + {\rm{d}}{T_{{\rm{min}}}}}}{2})\\ {\rm{d}}{s^*} = {K_s}({\rm{d}}s - \frac{{{\rm{d}}{s_{{\rm{max}}}} + {\rm{d}}{s_{{\rm{min}}}}}}{2}) \end{array} \right. $ | (4) |
式中:dT*, ds*为变换到标准论域的输入量;dTmax, dTmin和dsmax, dsmin分别为实际输入所在研究范围的最大最小值;K′T,Ks分别为温度变化和形变变化输入变换的比例因子。
(2) 模糊推理
模糊推理基于模糊逻辑中蕴涵关系及推理规则来进行。本文采用模糊蕴涵最小运算(Mamdani)实现模糊推理[10]。
对于两输入单输出的模糊推理单元,已建立的模糊规则库为:
R1:如果x是A1, y是B1,则z是C1
R2:如果x是A2, y是B2,则z是C2
…
Rn:如果x是An, y是Bn,则z是Cn
其中:x, y和z为分别代表输入和输出的语言变量,Ai,Bi和Ci(i=1, 2, …, n)分别是语言变量x, y和z在其论域X,Y,Z上的语言变量值,所有规则组合在一起构成了规则库。
对于第i条规则“如果x是Ai, y是Bi,则z是Ci”的模糊蕴涵关系Ri定义为
| $ {\mathit{\boldsymbol{R}}_i} = \left( {{\mathit{\boldsymbol{A}}_i}\;\;{\rm{and}}\;{\mathit{\boldsymbol{B}}_i}} \right) \to {\mathit{\boldsymbol{C}}_i} $ | (5) |
式中:(Ai and Bi)为定义在X×Y上的模糊集合Ai×Bi,Ri=(Ai and Bi)→Ci是定义在X×Y×Z上的模糊蕴涵关系。
所有n条模糊规则总的模糊蕴涵关系为
| $ \mathit{\boldsymbol{R = }}\bigcup\limits_{i = 1}^n {{\mathit{\boldsymbol{R}}_i}} $ | (6) |
(3) 清晰化
清晰化的作用是将模糊推理得到的模糊量变换为实际的清晰量, 采用文献[11]的清晰化方法。
| $ {z_0} = \frac{{\sum\limits_{i = 1}^7 {\sum\limits_{j = 1}^7 {{z_{0, l(i, j)}}{\mu _{l(i, j)}}} } }}{{\sum\limits_{i = 1}^7 {\sum\limits_{j = 1}^7 {{\mu _{l(i, j)}}} } }} $ | (7) |
式中:μl(i, j)为触发不同模糊规则的隶属度,z0, l(i, j)为输出模糊集所对应的中心值。
输出量进行尺度变换,变换到实际的论域范围
| $ \Delta {\lambda _\alpha } = {K_\alpha }\Delta \lambda _\alpha ^* + \frac{{\Delta {\lambda _{\alpha \;{\rm{max}}}} + \Delta {\lambda _{\alpha \;{\rm{min}}}}}}{2} $ | (8) |
| $ \Delta {\lambda _\beta } = {K_\beta }\Delta \lambda _\beta ^* + \frac{{\Delta {\lambda _{\beta \;{\rm{max}}}} + \Delta {\lambda _{\beta \;{\rm{min}}}}}}{2} $ | (9) |
式中:Δλα*, Δλβ*为清晰化后标准论域的输出量; Δλα, Δλβ为变换到实际论域的输出量; Kα, Kβ为输出变换的比例因子。
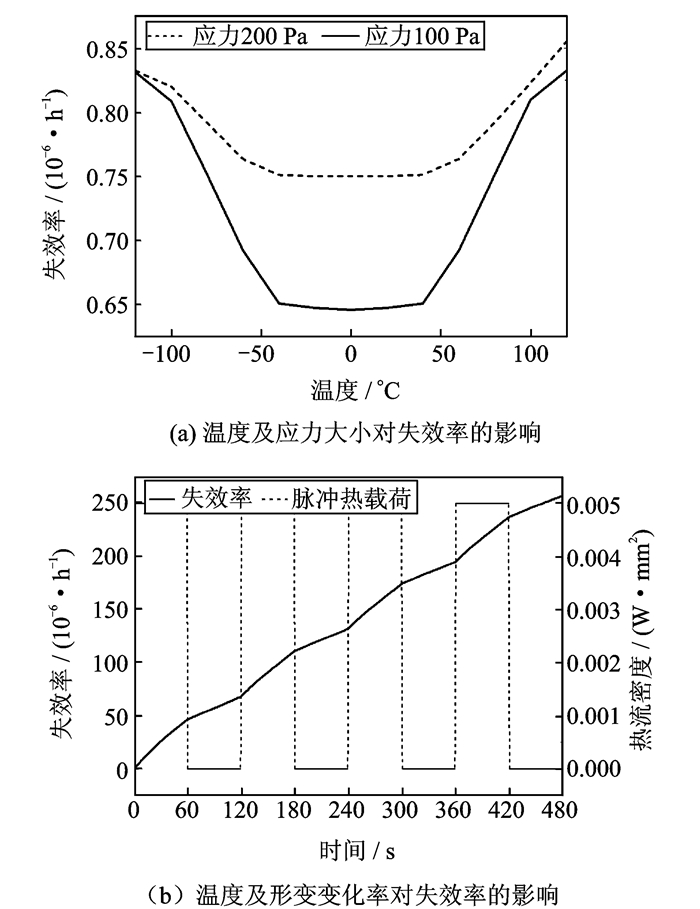
3 仿真校验 3.1 温度及应力大小对失效率的影响在一定高温范围内,随着温度的升高,失效率呈指数函数逐渐升高;当温度较低时,随着温度的减小,失效率也在升高,这主要是由于低温引起的材料冷脆所导致的。同样温度一定的情况下,应力较大导致机械失效,故失效率增加。
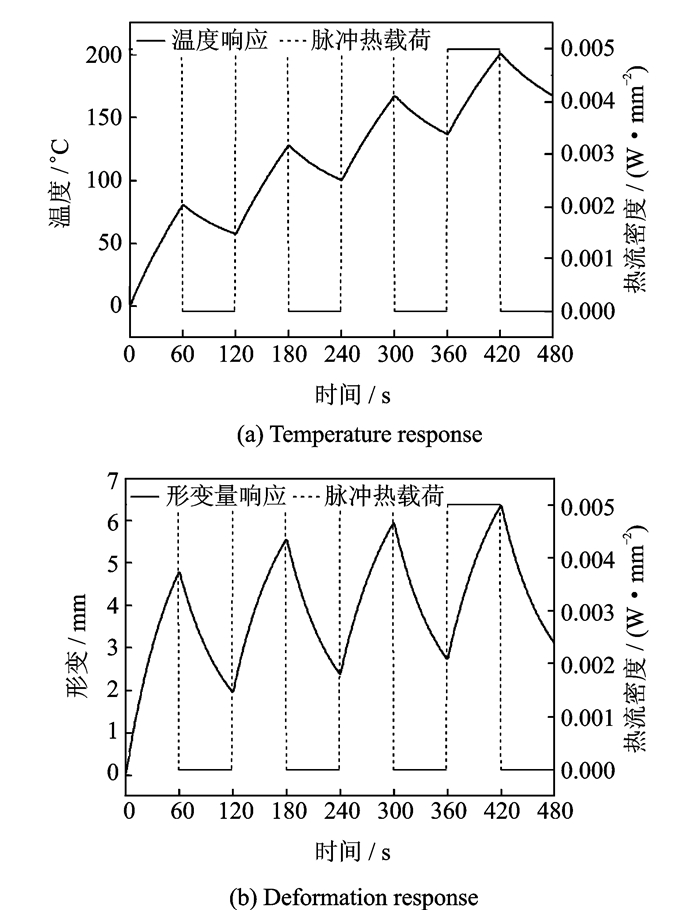
3.2 温度及形变变化率对失效率的影响ANSYS仿真,每隔1 min施加5 000 W的热流密度载荷,研究算例的温度响应及形变响应,将每秒的温度变化和形变变化作为输入,温度及形变在脉冲载荷条件下响应如图 4所示。经过模糊推理可得失效率的相对变化,温度及应力的大小和变化率对失效率的影响如图 5所示。
|
图 4 脉冲载荷输入及其响应 Figure 4 Pulse load input and its response |
|
图 5 仿真结果 Figure 5 Simulation results |
随着温度和形变的增加,失效率也在增加;随着循环次数的增加,失效率不断上升;0~60 s时间段内,温度形变上升,初始斜率较大,温度及形变相对上一时刻变化较大,失效率的变化量较大,随着斜率减小,失效率的变化量减小,但是累加失效率在上升,上升的斜率在减小;60~120 s时间段内,虽然温度和形变在冷却过程下降,但是斜率依然存在,即温度和形变相对前一时刻仍在变化,故失效率相对变化,随着斜率的降低,失效率的相对变化在逐渐下降,但总的累加失效率仍在上升,反应了温度形变不断变化对失效率的影响。
4 结束语本文采用基于模糊逻辑的智能算法,研究了温度和应力大小对失效率的影响,以及温度和形变相对于上一时刻的变化对失效率的影响。本文研究有效解决了定性分析到定量计算的过渡以及传统数学模型数据缺失等问题,为航天电子元器件的可靠性分析提供有效的失效率计算方法。
| [1] |
夏贵斌, 黄政.
多种负荷下的电子元器件突然失效率估算方法[J]. 中国设备工程, 2009(7): 47–49, 57.
DOI:10.3969/j.issn.1671-0711.2009.07.024 XIA Guibin, HUANG Zheng. Estimation method of sudden failure rate of electronic components under the effect of multi-load[J]. China Plant Engineering, 2009(7): 47–49, 57. DOI:10.3969/j.issn.1671-0711.2009.07.024 |
| [2] |
SEO H S, RHEE J.
Thermal failure of the LM117 regulator under harsh space thermal environments[J]. Dialogues in Cardiovascular Medicine DCM, 2013, 27(1): 49–56.
|
| [3] |
闵桂荣.
卫星热控制技术[M]. 北京: 宇航出版社, 1991: 25-28.
|
| [4] |
LUO Y, JIANG W.
Effects of anode porosity on thermal stress and failure probability of planar solid oxide fuel cell with bonded compliant seal[J]. International Journal of Hydrogen Energy, 2016, 41(18): 7464–7474.
DOI:10.1016/j.ijhydene.2016.03.117
|
| [5] |
CELINA M, GILLEN K T, ASSINK R A.
Accelerated aging and lifetime prediction:Review of non-Arrhenius behaviour due to two competing processes[J]. Polym Degrad Stab, 2005, 90: 395.
DOI:10.1016/j.polymdegradstab.2005.05.004
|
| [6] |
中国人民解放军总装备部. GJB/Z 299C-2006: 电子设备可靠性预计手册[S].北京: [s.n.], 2006.
|
| [7] |
ZADEH L A.
Fuzzy sets, information and control[J]. Information & Control, 1965, 8(3): 338–352.
|
| [8] |
KLIR J, YUAN B.
Fuzzy sets and fuzzy logic:Theory and applications[M]. New Jersey: Prentice Hall, 1995.
|
| [9] |
YADAV O P, SINGH N.
A fuzzy logic based approach to reliability improvement estimation during product development[J]. Reliability Engineering and System Safety, 2003, 80: 63–74.
DOI:10.1016/S0951-8320(02)00268-5
|
| [10] |
李国勇, 杨丽娟.
神经·模糊·预测控制及其MATLAB实现[M]. 北京: 电子工业出版社, 2013: 187-222.
|
| [11] |
LI Y Z, LEE K M.
Thermohydraulic dynamics and fuzzy coordination control of a microchannel cooling network for space electronics[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 700–708.
DOI:10.1109/TIE.2010.2045999
|
 2018, Vol. 50
2018, Vol. 50


