地空导弹在执行防空作战任务时,发射装置中的复合随动系统同步跟踪和随动性能的准确性直接影响导弹武器作战的效能。导弹复合随动系统运动特性校准主要采用分系统静态校准方法,该方法具有校准方式简单、校准设备成熟、安装操作简单等特点,是目前广泛采用的校准方式[1]。然而传统的分系统静态校准方法在测量效率、测量便捷性以及随动系统运动状态复现性上存在一些不足:使用分系统静态校准方法,只是对复合随动系统不同方位姿态角进行校准,测量效率低,没有结合复合随动系统实际工况及测试状态开展校准,且缺乏符合要求的校准规范指导。
为解决上述问题,本文提出使用多目视觉动态测量系统来实现复合随动系统运动特性的现场动态校准。利用多目视觉动态测量系统实现复合随动系统上方位随动系统和高低随动系统上被测标志点的实时跟踪测量,具有测量精度高、速度快、成本低和自动化程度高等优点。
1 导弹复合随动系统的工作原理本文的被测对象随动系统是一种用于倾斜发射的导弹发射架结构。图 1为随动系统结构原理图。发射架一端通过联结轴安装在方位转台上,另一端与俯仰推举缸伸出端相连,俯仰推举缸固定端与方位转台连接;发射架和相关控制系统组成高低随动系统,方位转台和相关控制系统组成方位随动系统,发射架、方位转台、俯仰推举缸和相关控制系统组成一整体机构——随动系统,实现发射架通过俯仰推举缸进行俯仰运动,并通过方位转台实现360°随动[2-4]。随动系统通过位置指令装置将希望的位移转换成具有一定精度的电量,利用为止反馈装置随时检测处被控机械的实际位移,也把它转换成具有一定精度的电量,与指令进行比较,把比较得到的偏差信号放大以后,控制执行电机向消除偏差的方向旋转。
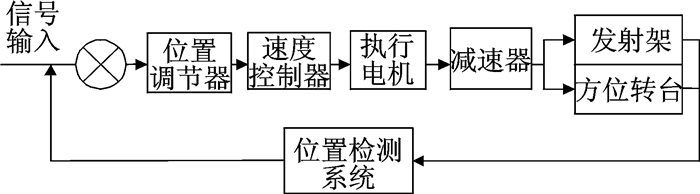
|
图 1 随动系统结构原理图 Figure 1 Structure schematic diagram of servo system |
2 基于多目视觉动态测量系统的校准方法 2.1 总体方案设计
本文采用多台高速相机在不同的位置动态或静态采集导弹发射车随动系统运动的图像,如图 2所示,通过系统软件的图像处理、分析计算和三维恢复等过程后,实时测量被测对象的空间位置、姿态等。
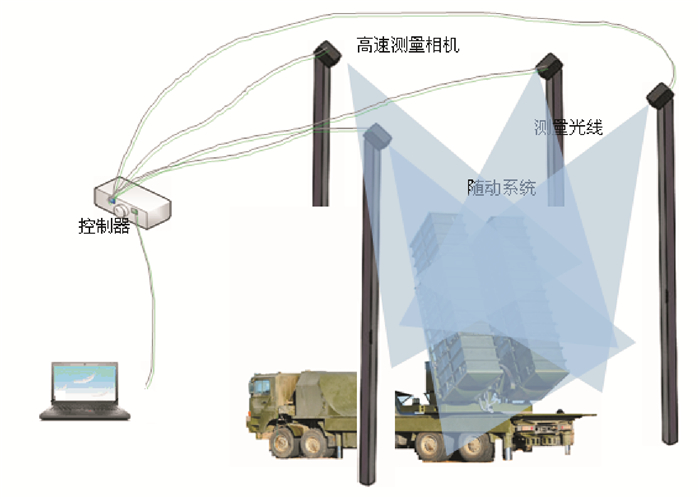
|
图 2 校准技术方案示意图 Figure 2 Calibration technology scheme diagram |
多目视觉动态测量系统由4台高速相机、图像采集控制器和系统软件等部件组成。主要构成为:
仪器主机:采用4台高速相机。单相机测量精度3 μm+3 μm/m。方位视场角81°,仰俯视场角60°,1台用于随动系统的基准测量,3台用于随动系统运动姿态测量。
图像采集同步控制器:同步控制器主要用于为多路相机及光源供电,并控制多台相机同步进行拍照,并将照片进行图像处理后传送给上位机进行解算。
软件:数据采集处理采用自主研发软件。
2.2 多目视觉动态测量系统原理及技术实现多目视觉动态测量是通过在不同的位置和方向获取同一物体的2幅不同角度的数字图像,经计算机图像匹配等处理及相关数学计算后得到待测点精确的三维坐标[5-7]。
多目视觉动态测量系统采用多摄站交会的几何原理,系统采用多个摄站对目标进行拍摄,可获取被测物体的多个立体像对,从而构成多目立体视觉[8-10],设物方点Pi由j个摄站(j条光线)相交(图 3),则共有j个共线方程:
| $ \left. \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x - {x_0} + \Delta x} \right)ij = \\ - {f_j}\frac{{{a_{{1_j}}}\left( {{X_i} - {X_{{S_j}}}} \right) + {b_{1j}}\left( {{Y_i} - {Y_{{S_j}}}} \right) + {c_{1j}}\left( {{Z_i} - {Z_{{S_j}}}} \right)}}{{{a_{3j}}\left( {{X_i} - {X_{{S_j}}}} \right) + {b_{3j}}\left( {{Y_i} - {Y_{{S_j}}}} \right) + {c_{3j}}\left( {{Z_i} - {Z_{{S_j}}}} \right)}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {y - {y_0} + \Delta y} \right)_{ij}} = \\ - {f_j}\frac{{{a_{2j}}\left( {{X_i} - {X_{{S_j}}}} \right) + {b_{2j}}\left( {{Y_i} - {Y_{{S_j}}}} \right) + {c_{2j}}\left( {{Z_i} - {Z_{{S_j}}}} \right)}}{{{a_{3j}}\left( {{X_i} - {X_{{S_j}}}} \right) + {b_{3j}}\left( {{Y_i} - {Y_{{S_j}}}} \right) + {c_{3j}}\left( {{Z_i} - {Z_{{S_j}}}} \right)}} \end{array} \right\} $ | (1) |
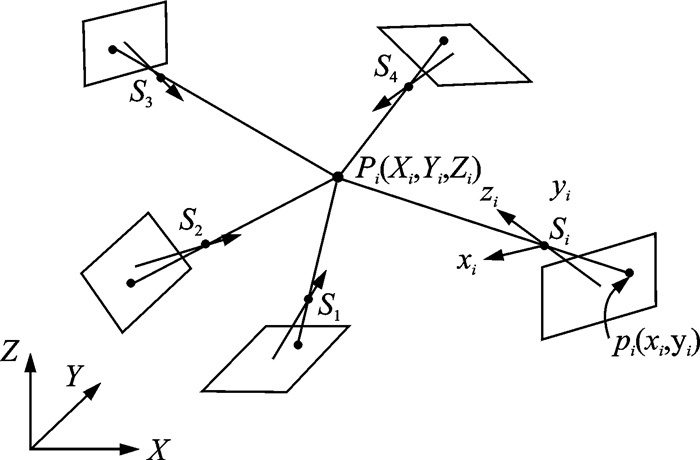
|
图 3 多摄站交会几何 Figure 3 Multi-station intersection geometric principle |
对共线方程式线性化得到像点坐标改正数方程式为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ \begin{array}{l} {v_x}\\ {v_y} \end{array} \right] = \\ \left[ \begin{array}{l} \frac{{\partial x}}{{\partial {X_S}}}\;\;\frac{{\partial x}}{{\partial {Y_S}}}\;\;\frac{{\partial x}}{{\partial {Z_S}}}\;\;\frac{{\partial x}}{{\partial \omega }}\;\;\frac{{\partial x}}{{\partial \varphi }}\;\;\frac{{\partial x}}{{\partial \kappa }}\;\;\frac{{\partial x}}{{\partial X}}\;\;\frac{{\partial x}}{{\partial Y}}\;\;\frac{{\partial x}}{{\partial Z}}\\ \frac{{\partial y}}{{\partial {X_S}}}\;\;\frac{{\partial y}}{{\partial {Y_S}}}\;\;\frac{{\partial y}}{{\partial {Z_S}}}\;\;\frac{{\partial y}}{{\partial \omega }}\;\;\frac{{\partial y}}{{\partial \varphi }}\;\;\frac{{\partial y}}{{\partial \kappa }}\;\;\frac{{\partial y}}{{\partial X}}\;\;\frac{{\partial y}}{{\partial Y}}\;\;\frac{{\partial y}}{{\partial Z}} \end{array} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ \begin{array}{l} \Delta {X_S}\\ \Delta {Y_S}\\ \Delta {Z_S}\\ \;\Delta \omega \\ \;\Delta \varphi \\ \;\Delta \kappa \\ \;\Delta X\\ \;\Delta Y\\ \;\Delta Z \end{array} \right] - \left[ \begin{array}{l} x - \overline X \\ y - \overline y \end{array} \right] \end{array} $ | (2) |
式中:x,y表示用近似参数计算的像点坐标。
将式中的未知数分为外方位元素、物方点坐标和内方位元素,则有
| $ \begin{array}{l} \left[ \begin{array}{l} {v_x}\\ {v_y} \end{array} \right] = \left[ \begin{array}{l} {c_{11}}\;\;{c_{12}}\;\;{c_{13}}\;\;{c_{14}}\;\;{c_{15}}\;\;{c_{16}}\\ {c_{21}}\;\;{c_{22}}\;\;{c_{23}}\;\;{c_{24}}\;\;{c_{25}}\;\;{c_{26}} \end{array} \right]\left[ \begin{array}{l} \Delta {X_S}\\ \Delta {Y_S}\\ \Delta {Z_S}\\ \;\Delta \omega \\ \;\Delta \varphi \\ \;\Delta \kappa \end{array} \right] + \\ \;\;\;\;\;\left[ \begin{array}{l} - {c_{11}}\;\; - {c_{12}}\;\; - {c_{13}}\\ - {c_{21}}\;\; - {c_{22}}\;\; - {c_{23}} \end{array} \right]\left[ \begin{array}{l} \Delta X\\ \Delta Y\\ \Delta Z \end{array} \right] - \left[ \begin{array}{l} {l_x}\\ {l_y} \end{array} \right] \end{array} $ | (3) |
写成矩阵形式,得到像点坐标误差方程式的一般式为
| $ \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{X}}_1}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{A}}_{\rm{2}}}{\mathit{\boldsymbol{X}}_2}\mathit{\boldsymbol{ - L}} $ | (4) |
为了验证随动系统运动特性动态校准方法的准确性,利用激光跟踪系统完成实验室环境下的多目视觉动态测量系统的试验验证。采用一定数量的特征编码点来确定相机之间的位置关系及姿态关系。首先在实验室环境下布设特征编码点,通过激光跟踪仪完成各特征编码点位置关系的校准,最后使用摄影测量系统识别已布设的特征点,自动完成相关匹配,并解算出已校准特征点的位置关系,然后完成其试验验证过程。
在四面体标准器上贴反光标志点,在边长分别为500 mm,800 mm,1000 mm上做3组实验,将实验结果与激光跟踪仪测量结果进行比较,结果如表 1所示。
| 表 1 准确度测试结果 Table 1 Accuracy test results |
从表 1可以发现,最大测试结果误差为0.051 mm,说明该摄影测量系统具有较高的准确度。
3.2 某型导弹随动系统运动特性现场测试采用多目视觉动态测量系统进行某型导弹运动特性现场测试。测试前,将高速相机动态多目视觉动态测量系统进行安装和连接,粘贴测量标识,分别建立发射车和随动系统坐标系,然后进行多相机姿态标定。测试时,随动系统进行联动,高速相机动态测量系统进行实时动态测量,数据处理软件实时计算出随动系统转动的角度、角速度和角加速度等动态参量,快速获取目标物在每个时刻的姿态角以及速度、加速度等动态参量,并与随动系统理论值进行比较,完成校准。图 4为随动系统运动参数动态校准结构框图,其测试结果如表 2所示。
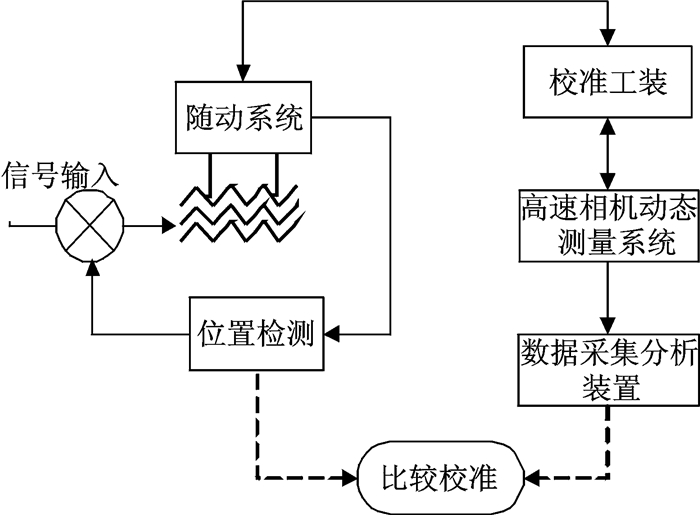
|
图 4 随动系统运动参数动态校准结构框图 Figure 4 Servo system motion parameters calibration block diagram |
| 表 2 随动系统运动参数测试结果 Table 2 Test results of servo system motion parameters |
从表 2可发现,多目视觉动态测量系统的速度测试结果的最大误差为0.072°/s,其相对误差为0.16%,角度测试的最大误差为0.024°,这说明多目视觉动态测量系统完全满足导弹随动系统运动特性的校准需求。
4 结论本文对某型导弹随动系统运动特性的校准设计了一种现场校准方式,对校准方法进行了研究,并阐述了某型导弹随动系统的校准原理。利用多目视觉动态测量系统进行分参数校准的方法有效地解决了某导弹随动系统运动特性的校准难题。精度测试和随动系统运动特性的现场校准试验结果表明,该方法可行,数据准确、可靠,大大提高了导弹随动系统运动特性校准的准确性。
| [1] |
贾云得.
机器视觉[M]. 北京: 科学出版社, 2000.
JIA Yunde. Machine vision[M]. Beijing: Science Press, 2000. |
| [2] |
蒋有才, 韩晓光, 赵玉龙, 等.
位置随动系统动态性能自动检测研究[J]. 军械工程学院学报, 2013, 25(5): 63–65.
DOI:10.3969/j.issn.1008-2956.2013.05.013 JIANG Youcai, HAN Xiaoguang, ZHAO Yulong, et al. Position servo system dynamic performance automatic detection[J]. Journal of Ordnance Engineering College, 2013, 25(5): 63–65. DOI:10.3969/j.issn.1008-2956.2013.05.013 |
| [3] |
黄富, 于正林.
随动系统运动参数测试研究[J]. 机械工程师, 2013(12): 106–109.
DOI:10.3969/j.issn.1002-2333.2013.12.054 HUANG Fu, YU Zhenglin. Study on motion parameters testing of the servo system[J]. Mechanical Engineer, 2013(12): 106–109. DOI:10.3969/j.issn.1002-2333.2013.12.054 |
| [4] |
郭海, 吴益飞, 郭毓.
车载发射转塔高性能随动系统智能控制策略研究[J]. 计算机测量与控制, 2012, 20(5): 1222–1224, 1228.
GUO Hai, WU Yifei, GUO Yu. Study on intelligent control strategy of a servo system in a car-borne launch turret with high performance[J]. Computer Measurement & Control, 2012, 20(5): 1222–1224, 1228. |
| [5] |
王德辉, 张世林, 王桂芝.
CCD技术与图像测量在叶片测量中的应用[J]. 计量与测试技术, 2002, 29(2): 17–19.
DOI:10.3969/j.issn.1004-6941.2002.02.009 WANG Dehui, ZHANG Shilin, WANG Guizhi. Application of CCD and image technique in the blade edge measurement[J]. Metrology & Measurement Technology, 2002, 29(2): 17–19. DOI:10.3969/j.issn.1004-6941.2002.02.009 |
| [6] |
JENSEN K, ANASTASSIOU D.
Sub-pixel edge localization and the interpolation of still images[J]. IEEE Trans Image Processing, 1995, 4(3): 285–295.
DOI:10.1109/83.366477
|
| [7] |
赵爱明.
基于二次曲线拟合的图像亚像素边缘定位算法[J]. 哈尔滨理工大学学报, 2006, 11(3): 68–70.
DOI:10.3969/j.issn.1007-2683.2006.03.022 ZHAO Aiming. Sub pixel detection algorithm based guadrativ cure fitting[J]. Journal of Harbin University of Science and Technology, 2006, 11(3): 68–70. DOI:10.3969/j.issn.1007-2683.2006.03.022 |
| [8] |
LYVERS E P, MITCHELL O R.
Precision edge contrast and orientation estimation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1988, 10(6): 927–937.
|
| [9] |
于起峰, 陆宏伟, 刘肖琳.
基于图像的精密测量与运动测量[M]. 北京: 科学出版社, 2002.
YU Qifeng, LU Hongwei, LIU Xiaolin. Precision measurement and motion measurement based on image[M]. Beijing: Science Press, 2002. |
| [10] |
孟祥丽, 周波, 程俊延, 等.
基于单相机的数字摄影测量系统关键技术研究[J]. 机床与液压, 2009, 37(1): 94–96, 170.
DOI:10.3969/j.issn.1001-3881.2009.01.032 MENG Xiangli, ZHOU Bo, CHENG Junyan, et al. Research on photogrammetry and 3D reconstructing system based on single cameras[J]. Machine Tool & Hydraulics, 2009, 37(1): 94–96, 170. DOI:10.3969/j.issn.1001-3881.2009.01.032 |
 2018, Vol. 50
2018, Vol. 50


