2. 北京理工大学信息与电子学院, 北京, 100081
2. School of Information & Electronics, Beijing Institute of Technology, Beijing, 100081, China
群时延特性是通信卫星转发器分系统重要的测试项目,而数字群时延测试法[1]是群时延特性测试的一种数字实现技术。由于该技术信号动态范围大、算法可重构、参数可灵活配置、测试精度高及设备集成性好,比矢量网络分析仪及其他测试技术具有较大的优势[1],因此广泛应用于通信卫星转发器测试领域。该方法设计之初是为了适应常规转发器(1~100 MHz带宽)的测试,随着通信卫星技术的不断发展,目前通信带宽已经向窄带宽(小于100 kHz)和宽带(大于100 MHz)两个方向拓展[2],该测试法已经无法满足不同带宽的测试需求。究其原因是不同带宽的测试参数和硬件环境选择不合理,由于测试参数与算法、硬件环境和通信带宽相关联,因此需要深入研究其中的关系,才能设计出合理的测试参数,进而优化测试系统。
本文将数字群时延测试法抽象成数学模型,并建立MATLAB仿真平台,通过仿真深入理解测试参数的深层意义,得出不同带宽的测试参数设计方法,并搭建硬件测试平台进行验证,最终满足不同带宽下的群时延测试需求。
1 数字群时延测试原理 1.1 群时延定义群时延是指群信号通过传输系统后,信号整体产生的延迟。假设通信系统的传递函数为[3]
| $ H\left( {{{\rm{e}}^{j\omega }}} \right) = A\left( \omega \right){{\rm{e}}^{{\rm{j}}\phi \left( \omega \right)}} $ | (1) |
式中:A(ω)和θ(ω)分别为系统的幅频特性函数和相频特性函数。
系统群时延特性τ(ω)可以表示为[3]
| $ \tau \left( \omega \right) = \frac{{{\rm{d}}\varphi \left( \omega \right)}}{{{\rm{d}}\omega }} $ | (2) |
如果群时延特性是平坦的,即式中τ(ω)是常数,则信号的不同频率分量具有相同时延,因此信号不会产生畸变;反之若群时延是波动的,即τ(ω)随频率变化,则信号的不同频率分量具有不同时延,因此信号会产生畸变[4]。
1.2 数字群时延测试方法数字群时延测试法是利用经过转发器的频率调制(Frequency modulation, FM)信号解调出的调制信号与未经转发器的原始调制信号的相位差[5]来计算转发器系统群时延,其测试原理如图 1所示,算法实现过程参见文献[1],这里不再赘述。

|
图 1 数字群时延测量原理框图 Figure 1 Block diagram of digital group delay test implementation |
2 MATLAB仿真模型建立及参数优化设计
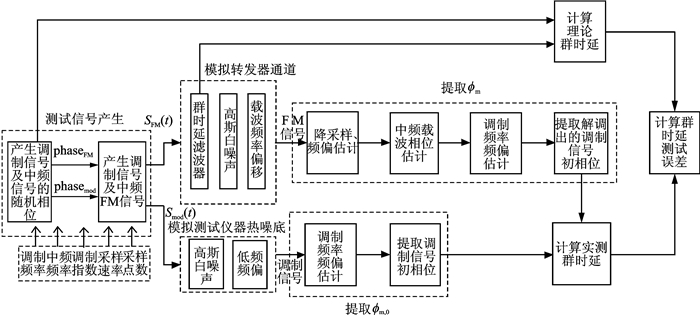
依据数字群时延测量原理[1],搭建MATLAB仿真平台,模拟转发器通道时延特性及测试链路热噪声特性,对系统收发全链路进行仿真,仿真链路如图 2所示。从算法原理[1]和系统仿真链路可以看出,本测试方法中涉及多个关键测量参数,其对不同转发器带宽下的群时延测量精度有不同影响。下面分别对各关键参数对测试精度的影响进行理论和仿真分析,并得出不同带宽下的转发器通道群时延各个测试参数的优化方法。
|
图 2 数字群时延测试MATLAB仿真链路 Figure 2 MATLAB simulation path link of digital group delay test |
2.1 调制频率
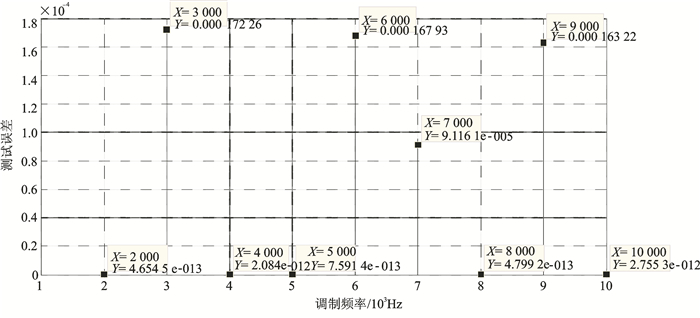
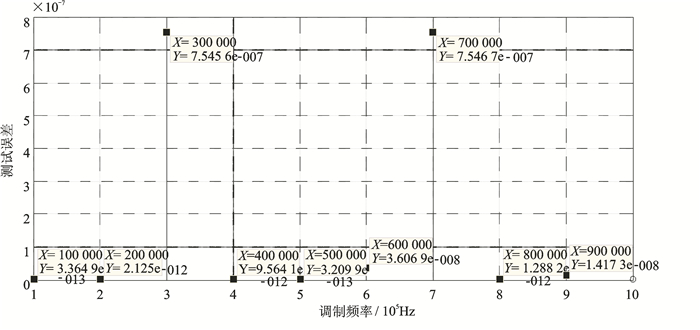
转发器通信带宽决定了FM信号的一阶分量[6]带宽,即调制频率。表 1提供了群时延误差随调制频率变化的仿真条件。仿真条件1结果如图 3所示,条件2如图 4所示,群时延误差随调制频率呈现非单调关系变化,在测试不同带宽下群时延时,首先应根据通信带宽大致选择调制频率量级,然后在此基础上通过仿真确定调制频率具体数值。
| 表 1 群时延随调制频率变化的仿真条件 Table 1 Simulation conditions for the change of delay with modulation frequency |
|
图 3 仿真条件1下群时延误差随调制频率的关系 Figure 3 Relationship of group delay error and modulation freqency in simulation 1 |
|
图 4 仿真条件2下群时延误差随调制频率的关系 Figure 4 Relationship of group delay error and modulation frequency in simulation 2 |
2.2 中频频率、采样速率、采样点数、系统频偏
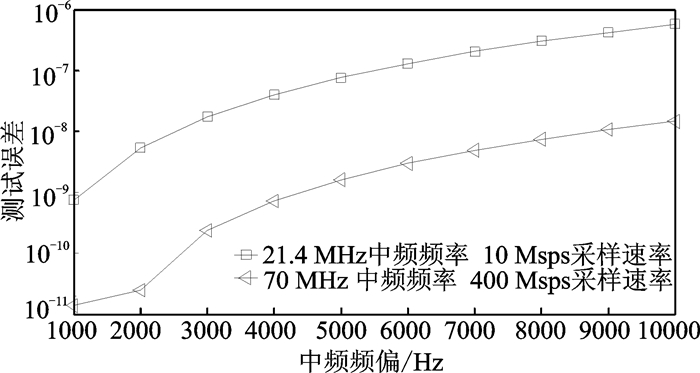
表 2给出了200 MHz通信带宽下群时延测量误差随中频频率、采样速率和中频频偏(系统固有频偏,指硬件的实际中频频率与算法中设置的频率之间的偏差)的仿真条件,其中中频频率和采样速率满足采样定律[7-8]。仿真结果如图 5所示,70 MHz中频、400 Msps采样速率测试结果精度较高,21.4 MHz中频、10 Msps采样速率的测试精度较低,同时随着系统频偏的增加,测量误差同步增加。因此,在确定调制频率后,依据测试设备的条件及能力,尽可能选择较大的中频和采样速率。同时,中频频偏是测试系统内各设备之间的频率偏差,将测试系统共时基,能够有效减少系统频率偏差。
| 表 2 群时延随其他参数变化的仿真条件 Table 2 Simulation conditions for the change of group delay with other parameters |
|
图 5 群时延测量误差随系统频偏变化仿真结果 Figure 5 Simulation results of the change of group delay test error with system frequency offset |
2.3 信噪比
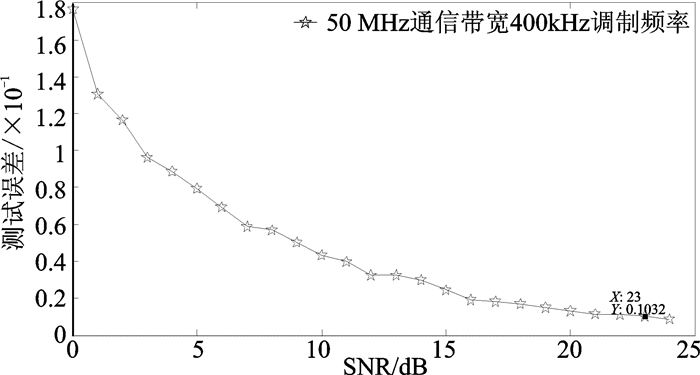
信噪比(Signal-nosie ratio, SNR)决定了下行链路测试设备输入信号的质量[9],表 3给出了群时延误差随信噪比变化的仿真条件,仿真结果如图 6所示,群时延误差随信噪比增大而减小。由于卫星转发器饱和输出电平为定值[2],提高下行链路的信噪比,需尽可能减小测试电缆或设备间的插损。
| 表 3 群时延误差随信噪比变化的仿真条件 Table 3 Simulation conditions of group delay with SNR |
|
图 6 群时延误差随信噪比变化关系曲线 Figure 6 Simulation of group delay error with SNR change |
2.4 不同带宽参数设计方法
综合以上仿真和分析过程,从而得出不同带宽的参数设计方法。
(1) 根据通信带宽选取调制频率量级,然后通过仿真结果得出最优调制频率;
(2) 中频频率和采样速率需满足采样定律[7]。中频频率可通过测试设备的能力来选择,Agilent E4447A提供21.4 MHz中频[10],Agilent N9030提供70MHz中频[11],采样速率依据示波器的能力来选择,采样点数影响算法的运行速度,采样速率和点数的选择需平衡硬件资源和测试效率;
(3) 中频频偏可以通过设备间共时基减弱其影响;信噪比可以通过减小下行链路插损来来实现。
综上所述,针对3种典型转发器带宽,表 4给出了群时延测试误差最小的参数设计。
| 表 4 针对不同带宽的MATLAB仿真最优参数 Table 4 Optimized parameters of MATLAB simulation according to different bandwidths |
3 工程实现测试验证
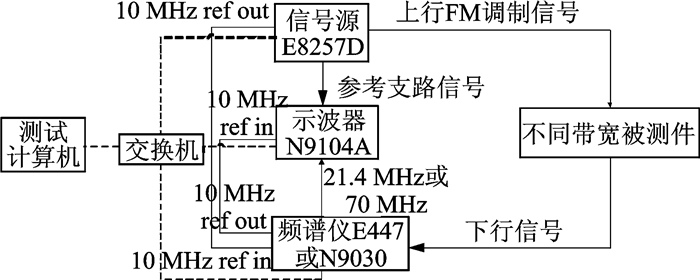
为验证以上仿真结果,搭建硬件测试系统,针对3种不同带宽进行测试验证。具体如图 7所示,其中不同带宽被测件包括40 kHz, 36 MHz和110 MHz模拟转发器。实测结果以群时延纹波(Group delay ripple)为衡量标准,它表征通信带宽内群时延的起伏程度[12],决定了通信信号的误差向量幅度(Error vector magnitude,EVM)[7],其测量结果包含了被测件真实的带内群时延起伏以及测试系统误差[8],而减少测试误差有助于真实反映被测件的群时延起伏程度。
|
图 7 硬件实验系统框图 Figure 7 Block diagram for hardware system implementation |
针对40 kHz窄带模拟器,调制频率可选取1 kHz至10 kHz之间, 群时延纹波在μs量级;针对36 MHz带宽模拟器,调制频率可选取400 kHz至800 kHz之间, 群时延纹波在ns量级;针对110 MHz宽带模拟器,调制频率可选取400 kHz至1 000 kHz之间, 群时延纹波在0.1 ns量级。表 5给出了实测结果,3种带宽的参数组3的群时延纹波明显低于其他两组参数,符合表 4中MATLAB仿真结果预期,达到了硬件验证的预期效果。
| 表 5 不同带宽模拟器工程验证情况 Table 5 Verification results with different bandwidths simulators |
4 结束语
本文首先简要介绍了数字群时延测试的基本原理,然后建立MATLAB仿真模型,分析了不同通信带宽下,测试参数对群时延测量误差的影响,并归纳出参数设计方法,最后,依据仿真结果,搭建3种不同带宽下的硬件测试系统。工程实测结果与仿真结果一致,满足了不同带宽下的群时延测试需求,进一步完善了数字群时延测试方法。本文所研究的数字群时延测试方法的最高精度能达到0.1 ns[11],和矢量网络分析仪测试精度相当,但由于该测试方法的信号源和频谱仪信号动态范围均大于矢量网络分析仪,因此该测试技术可以应用卫星转发器在轨测距、微波高精度测距、长电缆时延测试和系统时延测试等测试领域。
| [1] |
刘彬, 刘枫, 刘崇华.
卫星群时延特性测量新方案的设计和实现[J]. 航天器工程, 2010, 19(1): 77–81.
DOI:10.3969/j.issn.1673-8748.2010.01.014 LIU Bin, LIU Feng, LIU Chaoghua. Design and implementation of a novel method for satellite group delay measurement[J]. Spacecraft Engineering, 2010, 19(1): 77–81. DOI:10.3969/j.issn.1673-8748.2010.01.014 |
| [2] |
BAKLANOV I G, PALKIN E A. The method for the satellite transponder group delay measurement[C]//The 2nd International Conerence on Satellite Communications. Moscow, Russia: IEEE, 1996: 124-128.http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=864261 |
| [3] |
郑君里.
信号与系统[M]. 北京: 高等教育出版社, 2000: 270-274.
ZHENG Junli. Signal and system[M]. Beijing: High Education Press, 2000: 270-274. |
| [4] |
MITOLA J.
The software radio architecture[J]. IEEE Communications Magazine, 1995, 33(5): 26–38.
DOI:10.1109/35.393001
|
| [5] |
YI F B. FPGA implementation of a fully digital FM demodulator[C]//International Conference on Communications System.2004: 446-450.http://www.researchgate.net/publication/4106376_FPGA_implementation_of_a_fully_digital_FM_demodulator |
| [6] |
SONG B S, LEE I S.
A digital FM demodulator for FM, TV, and wireless[J]. IEEE Transactions on Circuits and Systems, 1995, 42(12): 821–825.
DOI:10.1109/82.476180
|
| [7] |
樊昌信.
通信原理[M]. 北京: 国防工业出版社, 2014: 187-193.
FAN Changxin. Communication[M]. Beijing: National Defence Industry Press, 2014: 187-193. |
| [8] |
NYQUIST H, BRAND S.
Measurement of phase distortion[J]. Bell System Technical Journal, 2014, 9(3): 522–549.
|
| [9] |
朱旭东.
系统绝对群时延测量的研究[J]. 现代雷达, 2006, 11: 75–80.
ZHU Xudong. Study of measurement for absolute group delay[J]. Modern Rador, 2006, 11: 75–80. |
| [10] |
Agilent Technologies. Understanding the fundamental principles of vector network analysis[Z]. Agilent Technologies, 2000: 1-14. |
| [11] |
Agilent Technologies. Applying error correction to network analyzer measurement[Z]. Agilent Technologies, 2004: 1-24. |
| [12] |
XI Qin.
Influence of group-delay ripple on timing jitter induced by SPM and IXPM in systems with dispersion compensated by CFBG[J]. Chinese Optics Letters, 2007, 5(8): 441–444.
|
 2018, Vol. 50
2018, Vol. 50


