2. 火箭军装备研究院, 北京, 100085
2. Rocket Force Equipment Academy, Beijing, 100085, China
命中精度是导弹的重要性能指标[1-2],如何对导弹的命中精度进行准确评估是亟待解决的一个重要问题。由于接近应用环境的导弹性能试验是小子样的,为了充分利用研制各阶段的飞行试验信息、仿真试验信息等先验信息,Bayes统计理论广泛应用于导弹命中精度评估[1]。
对于地面点目标而言,圆概率偏差(Circular error probability,CEP)是衡量导弹命中精度的关键指标[3-4],而对于舰船目标而言,常常采用命中概率来衡量反舰导弹的命中精度。对于命中概率的评估,经典的评估方法包括估计和假设检验,估计方法包括基于正态分布的命中概率Bayes估计[5]和基于二项分布的命中概率Bayes估计[6]。基于正态分布的命中概率Bayes估计假设导弹的落点偏差服从二维正态分布,通过估计正态分布的总体参数,进一步估计导弹命中目标区域的概率。基于二项分布的命中概率Bayes估计根据导弹是否命中目标区域确定成败,通过估计二项分布的成功概率参数,来估计导弹的命中概率。不论采用哪种评估方法,评估的完整流程是给定置信度,利用导弹试验数据估计得到导弹命中概率置信下限,与预先设定的精度指标进行比较,判断导弹在该置信度下是否满足精度要求。
在实际应用过程中,基于正态分布和基于二项分布的命中概率Bayes估计存在一定差异,单独使用可能会带来较大的评估风险。随着武器装备的不断发展,各种型号的反舰导弹层出不穷,对命中精度的评估要求越来越高,急需更稳健的精度评估方法。因此,本文结合Bootstrap重采样[7],基于正态分布提出了命中概率估计的新方法,并联合基于二项分布的命中概率估计,对导弹命中精度进行一致性评估。结果表明,该方法可以提高评估结果的稳健性,降低评估风险。
1 基于正态分布的命中概率Bayes估计为了估计导弹的命中概率,首先需要估计导弹落点的正态分布参数。基于二维的正态密度函数,在命中区域内进行积分,可以得到命中概率的点估计,但是经典方法难以给出命中概率的区间估计及置信下限估计,因此在本节基于Bootstrap重采样构建了计算命中概率区间估计及置信下限估计的新方法。
1.1 正态参数的Bayes估计假设导弹的落点偏差服从二维正态分布,为方便讨论,以X方向为例,介绍正态参数的Bayes估计。设X~N(μ, D),其中μ是均值,D是方差。考虑μ, D均未知的情况,(μ, D)的共轭先验分布为正态逆Gamma分布[8-9]。将前一阶段的数据作为后续阶段的先验信息,可得到多阶段试验之下的Bayes递推估计。
记
| $ \pi \left( {\mu ,D\left| {{{\bar X}^{\left( 1 \right)}},{u^{\left( 1 \right)}}} \right.} \right) \propto N\left( {{\mu _1},{\eta _1}D} \right) \cdot {\mathit{\Gamma }^{ - 1}}\left( {{\alpha _1},{\beta _1}} \right) $ | (1) |
式中,Γ-1(α1, β1)表示以α1, β1分布参数的逆Gamma分布密度函数,若先验分布采用无先验信息时的π(μ, D)∝1/D,故有
| $ \left\{ \begin{array}{l} {\alpha _1} = \sum\limits_{i = 1}^{{n_1}} {{{\left( {X_i^{\left( 1 \right)} - {{\bar X}^{\left( 1 \right)}}} \right)}^2}/2} = {n_1}{u^{\left( 1 \right)}}/2\\ {\beta _1} = \left( {{n_1} - 1} \right)/2\\ {\mu _1} = {{\bar X}^{\left( 1 \right)}}\\ {\eta _1} = 1/{n_1} \end{array} \right. $ | (2) |
式中
| $ \left\{ \begin{array}{l} {{\bar X}^{\left( 1 \right)}} = \frac{1}{{{n_1}}}\sum\limits_{i = 1}^{{n_1}} {X_i^{\left( 1 \right)}} \\ {u^{\left( 1 \right)}} = \frac{1}{{{n_1}}}\sum\limits_{i = 1}^{{n_1}} {{{\left( {X_i^{\left( 1 \right)} - {{\bar X}^{\left( 1 \right)}}} \right)}^2}} \end{array} \right. $ | (3) |
同理,当进行第二阶段试验后,得到试验样本(X1(2), X2(2), …, X(2)n2),此时(μ, D)的后验联合概率密度
| $ \pi \left( {\mu ,D\left| {{{\bar X}^{\left( 2 \right)}},{u^{\left( 2 \right)}}} \right.} \right) \propto N\left( {{\mu _2},{\eta _2}D} \right) \cdot {\mathit{\Gamma }^{ - 1}}\left( {{\alpha _2},{\beta _2}} \right) $ | (4) |
故有
| $ \left\{ \begin{array}{l} {\alpha _2} = {\alpha _1} + \frac{{{n_2}{u^{\left( 2 \right)}}}}{2} + \frac{{{n_2}{{\left( {{{\bar X}^{\left( 2 \right)}} - {\mu _1}} \right)}^2}}}{{2\left( {{n_2}{\eta _1} + 1} \right)}}\\ {\beta _2} = {\beta _1} + {n_2}/2\\ {\eta _2} = \frac{{{\eta _1}}}{{1 + {n_2}{\eta _1}}} = \frac{1}{{{n_1} + {n_2}}}\\ {\mu _2} = \frac{{{n_2}{{\bar X}^{\left( 2 \right)}} + {\mu _1}/{\eta _1}}}{{{n_2} + 1/{\eta _1}}} \end{array} \right. $ | (5) |
式中
| $ \left\{ \begin{array}{l} {{\bar X}^{\left( 2 \right)}} = \frac{1}{{{n_2}}}\sum\limits_{i = 1}^{{n_2}} {X_i^{\left( 2 \right)}} \\ {u^{\left( 2 \right)}} = \frac{1}{{{n_2}}}\sum\limits_{i = 1}^{{n_2}} {{{\left( {X_i^{\left( 2 \right)} - {{\bar X}^{\left( 2 \right)}}} \right)}^2}} \end{array} \right. $ | (6) |
一般地,N个阶段之后,有
| $ \pi \left( {\mu ,D\left| {{{\bar X}^{\left( N \right)}},{u^{\left( N \right)}}} \right.} \right) \propto {\rm{N}}\left( {{\mu _N},{\eta _N}D} \right) \cdot {\mathit{\Gamma }^{ - 1}}\left( {{\alpha _N},{\beta _N}} \right) $ | (7) |
式中参数
这样,μ的后验边缘密度为
| $ \pi \left( {\mu \left| {{{\bar X}^{\left( N \right)}},{u^{\left( N \right)}}} \right.} \right) = \int_0^{ + \infty } {{\rm{ \mathsf{ π} }}\left( {\mu ,D\left| {{{\bar X}^{\left( N \right)}},{u^{\left( N \right)}}} \right.} \right){\rm{d}}D} $ | (8) |
而D的后验边缘密度为
| $ \pi \left( {D\left| {{{\bar X}^{\left( N \right)}},{u^{\left( N \right)}}} \right.} \right) = \int_{ - \infty }^{ + \infty } {{\rm{ \mathsf{ π} }}\left( {\mu ,D\left| {{{\bar X}^{\left( N \right)}},{u^{\left( N \right)}}} \right.} \right){\rm{d}}\mu } $ | (9) |
在平均损失函数之下,μ和D的Bayes估计分别为各自边缘分布的期望
| $ \left\{ \begin{array}{l} {{\hat \mu }_B} = {\mu _N}\\ {{\hat D}_B} = {\alpha _N}/\left( {{\beta _N} - 1} \right) \end{array} \right. $ | (10) |
(1) 假设落点的纵向偏差X和横向偏差Y是相互独立的正态随机变量,即
| $ X \sim N\left( {{\mu _x},{D_x}} \right),Y \sim N\left( {{\mu _y},{D_y}} \right) $ | (11) |
式中
| $ P = {P_x} \cdot {P_y} $ | (12) |
式中
| $ \begin{array}{l} {P_x} = P\left\{ {{x_1} \le x \le {x_2}} \right\} = \mathit{\Phi }\left[ {\left( {{x_2} - {\mu _x}} \right)/\sqrt {{D_x}} } \right] - \\ \;\;\;\;\;\;\;\mathit{\Phi }\left[ {\left( {{x_1} - {\mu _x}} \right)/\sqrt {{D_x}} } \right]\\ {P_y} = P\left\{ {{y_1} \le y \le {y_2}} \right\} = \mathit{\Phi }\left[ {\left( {{y_2} - {\mu _y}} \right)/\sqrt {{D_y}} } \right] - \\ \;\;\;\;\;\;\;\mathit{\Phi }\left[ {\left( {{y_1} - {\mu _y}} \right)/\sqrt {{D_y}} } \right] \end{array} $ | (13) |
Φ[·]表示标准正态分布的分布函数。
(2) 当X和Y不是相互独立的时候,假设(X, Y)服从二维正态分布N(μ, Σ),其中
| $ \mathit{\boldsymbol{\mu }} = \left\{ {\begin{array}{*{20}{c}} {{\mu _x}}\\ {{\mu _y}} \end{array}} \right\},\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = \left\{ {\begin{array}{*{20}{c}} {{D_x}}&{\rho \sqrt {{D_x}{D_y}} }\\ {\rho \sqrt {{D_x}{D_y}} }&{{D_y}} \end{array}} \right\} $ | (14) |
落点偏差(X, Y)的概率密度函数
| $ \begin{array}{l} f\left( {x,y} \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}\sqrt {{D_x}} \sqrt {{D_y}} \sqrt {1 - {\rho ^2}} }} \times \exp \left\{ { - \frac{1}{{2\left( {1 - {\rho ^2}} \right)}}} \right.\\ \left. {\left[ {\frac{{{{\left( {x - {\mu _x}} \right)}^2}}}{{{D_x}}} - \frac{{2\rho \left( {x - {\mu _x}} \right)\left( {z - {\mu _y}} \right)}}{{\sqrt {{D_x}} \sqrt {{D_y}} }} + \frac{{{{\left( {z - {\mu _y}} \right)}^2}}}{{{D_y}}}} \right]} \right\} \end{array} $ | (15) |
式中
| $ \rho = \frac{{\sum\limits_{i = 1}^n {\left[ {\left( {{x_i} - {\mu _x}} \right)\left( {{y_i} - {\mu _y}} \right)} \right]} }}{{\sqrt {\left[ {\sum\limits_{i = 1}^n {{{\left( {{x_i} - {\mu _x}} \right)}^2}} } \right]} \sqrt {\left[ {\sum\limits_{i = 1}^n {{{\left( {{y_i} - {\mu _y}} \right)}^2}} } \right]} }} $ | (16) |
则导弹的命中概率P为
| $ P = \iint_R {f\left( {x,y} \right){\text{d}}x{\text{d}}y} $ | (17) |
式(17)中积分的计算可采用数值积分法。
1.3 命中概率的区间估计以X和Y不独立情况为例,给出命中概率P的区间估计,置信下限估计。由于很难构造命中概率P的枢轴变量,因此无法基于经典统计方法给出P的区间估计,置信下限估计。
因此提出了基于Bootstrap方法的参数自助法,来计算P的区间估计,置信下限估计。设
(1) 根据试验样本,估计均值
(2) 从正态总体N(μ, Σ)中,随机抽取M组样本量为n的独立样本,利用式(17)计算出这M(1 000≤M≤3 000)个P的代入型点估计,并从小到大排序为
(3) 则P的置信度为1-α的置信区间估计为
假设n次导弹试验中导弹命中目标区域R的次数记作X,X服从二项分布B(n, P),其中P表示导弹的命中概率,P的共轭先验分布为Beta分布,记为B(α, β) [8-9],其中α, β是Beta分布的参数。
设先验试验结果成功数为s0,失败数为f0,先验试验数n0=s0+f0。若无先验信息可用,则按照Jeffreys规则,取s0=1/2,f0=1/2。先验分布为
| $ {\alpha _0} = {s_0},{\beta _0} = {f_0} $ | (18) |
设现场试验结果成功数为s1,失败数为f1,试验数n1=s1+f1,则后验分布为
| $ {\alpha _1} = {\alpha _0} + {s_1},{\beta _1} = {\beta _0} + {f_1} $ | (19) |
在平均损失函数下,P的Bayes点估计为
| $ \hat P = \frac{{{\alpha _1}}}{{{\beta _1}}} = \frac{{{s_0} + {s_1}}}{{{n_0} + {n_1}}} $ | (20) |
由文献[10]构造二项分布参数P的枢轴变量,可得到
| $ \frac{{{f_0} + {f_1}}}{{{s_0} + {s_1}}} \cdot \frac{P}{{1 - P}} \sim F\left( {2\left( {{s_0} + {s_1}} \right),2\left( {{f_0} + {f_1}} \right)} \right) $ | (21) |
式中F(·,·)表示F分布,故有
| $ {\text{Prob}}\left\{ {{F_{\alpha /2}} \leqslant \frac{{{f_0} + {f_1}}}{{{s_0} + {s_1}}} \cdot \frac{P}{{1 - P}} \leqslant {F_{1 - \alpha /2}}\left| X \right.} \right\} = 1 - \alpha $ | (22) |
其中Fα/2为
| $ \begin{array}{l} \left[ {\frac{{\left( {{s_0} + {s_1}} \right){F_{\alpha /2}}}}{{\left( {{f_0} + {f_1}} \right) + \left( {{s_0} + {s_1}} \right){F_{\alpha /2}}}},} \right.\\ \left. {\frac{{\left( {{s_0} + {s_1}} \right){F_{1 - \alpha /2}}}}{{\left( {{f_0} + {f_1}} \right) + \left( {{s_0} + {s_1}} \right){F_{1 - \alpha /2}}}}} \right] \end{array} $ | (23) |
P的1-α置信下限
| $ {{\hat P}_{L.B}} = \frac{{\left( {{s_0} + {s_1}} \right){F_\alpha }}}{{\left( {{f_0} + {f_1}} \right) + \left( {{s_0} + {s_1}} \right){F_\alpha }}} $ | (24) |
导弹精度试验中,落点位置服从正态分布,试验的目标区域为R=[-500, 500], [-200, 200]。若某型号导弹现场试验的落点偏差样本为:
| $ \mathit{\boldsymbol{X}} = \left[ { - 31.9, - 183.5,125.1, - 5.4, - 135.9} \right], $ |
| $ \mathit{\boldsymbol{Y}} = \left[ { - 33.8, - 101.1, - 31.1, - 6.4, - 45.8} \right]。$ |
该型号导弹研制阶段的飞行试验样本作为精度评估的先验样本,记作:X0=[60.6,-169.3,509.4,-320.0,203.9],Y0=[67.4,-21.9,-30.9,-5.8,-131.9]。
利用本文提出的基于正态分布的命中概率估计新方法及经典二项分布命中概率方法估计该批次导弹试验命中概率及置信下限,结果如表 1所示。
| 表 1 命中概率的估计结果 Table 1 Estimation results of hit probability |
3.2 两种评估方法的一致性分析
(1) 例1
为了分析两种评估方法的一致性,设置了不同的精度指标P0(从0到1),分别采用这两种评估方法进行评估,分析评估的结果。设两种方法可信度为90%的置信下限估计分别为
|
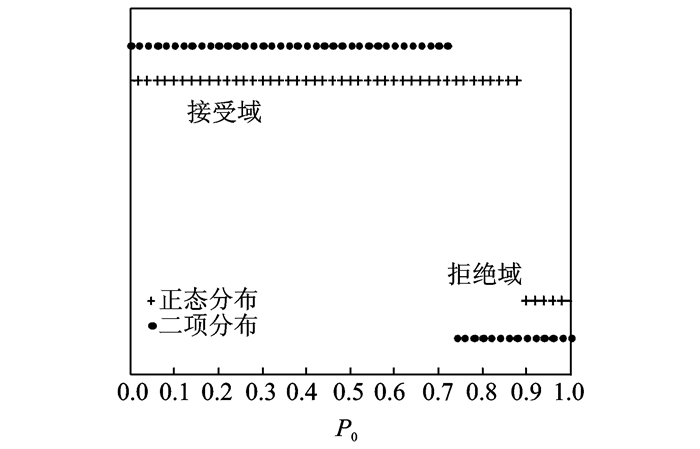
图 1 两种方法的评估结果 Figure 1 Assessment results of the two methods 注:横坐标(无单位)表示精度指标,纵坐标(无单位)高位表示估计结果满足精度指标,纵坐标低位表示估计结果不满足精度指标 |
从图 1可以看到,对于不同的精度指标,只要基于二项分布的评估结果满足精度要求,则基于正态分布的评估结果一定可以满足精度要求。因此从一定程度上讲,基于二项分布的评估准则更加宽容,而正态分布的评估准则更加严苛。
(2) 例2
假设另有某型号导弹现场试验的落点偏差样本为:X=[-122.7, -279. 3, 29.5,55.9,71.4],Y=[66.5, -59.2, -24.7,166.7,-98.5]。
该型号导弹研制阶段的飞行试验样本作为精度评估的先验样本,记作: X0=[-164.3,-45.5,445.1,242.3,-96.1],Y0=[143.4,-144.6,33.6,-110.5,-81.2]。
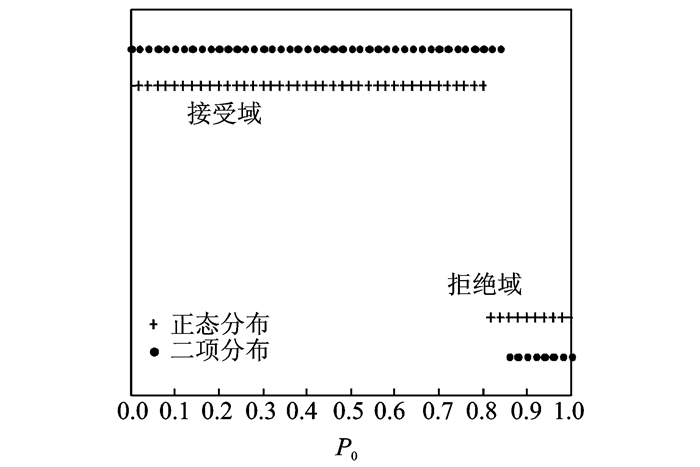
分别采用本文提到的两种方法进行评估,估计命中概率的置信下限,从而比较两种评估方法的差异,结果如图 2所示。
|
图 2 两种方法的评估结果 Figure 2 Assessment results of the two methods 注:横坐标(无单位)表示精度指标,纵坐标(无单位)高位表示估计结果满足精度指标,纵坐标低位表示估计结果不满足精度指标 |
从图 2可以看到,基于二项分布的评估结果满足精度要求时,基于正态分布的评估结果不一定满足精度要求,这与例一中得出的结论是矛盾的。
4 结论综合分析例一和例二的计算结果可以得到,对于不同型号的导弹试验,采用不同的评估方法得到的评估结果存在差异。因此,在对导弹试验进行精度评定的时候,应该综合考虑这两种评估方法的结果,只有两种方法的评估结果同时满足精度要求的时候,才判定导弹试验满足精度要求。
对于导弹试验评估而言,由于多源试验信息复杂,接近应用环境的性能试验子样数少,单独使用经典的评估方法对命中概率进行估计时,会造成较大的评估风险,估计的结果不稳健。本文改进了基于正态分布的命中精度估计方法,提出了基于Bootstrap重采样的命中概率区间估计新方法。综合基于正态分布和二项分布的命中概率评估方法进行一致性评估,在一定程度上可以降低评估风险,提高了估计结果的稳健性。
| [1] |
傅惠民.
导弹命中精度整体推断方法[J]. 北京航空航天大学学报, 2006, 32(10): 1141–1145.
DOI:10.3969/j.issn.1001-5965.2006.10.004 FU Huimin. Integral inference method for missile hit accuracy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(10): 1141–1145. DOI:10.3969/j.issn.1001-5965.2006.10.004 |
| [2] |
张金槐, 唐雪梅.
Bayes方法[M]. 长沙: 国防科技大学出版社, 1993.
|
| [3] |
汶小泥, 祝小平.
命中精度CEP的估计[J]. 弹箭与制导学报, 2005, 25(2): 367–369.
DOI:10.3969/j.issn.1673-9728.2005.02.120 WEN Xiaoni, ZHU Xiaoping. Evaluation of hit precision CEP[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2005, 25(2): 367–369. DOI:10.3969/j.issn.1673-9728.2005.02.120 |
| [4] |
ZHANG S, DUAN X, LI C, et al.
CEP calculation based on weighted Bayesian mixture Model[J]. Mathematical Problems in Engineering, 2017(5): 1–7.
|
| [5] |
金振中, 曲宝忠.
正态总体参数的Bayes评估及其应用[J]. 现代防御技术, 1996(2): 50–57.
JIN Zhenzhong, QU Baozhong. Bayesian evaluation of normal population parameters and its application[J]. Modern Defence Technology, 1996(2): 50–57. |
| [6] |
赵喜春.
导弹命中精度综合鉴定方法研究[J]. 现代防御技术, 2008, 36(3): 33–36.
ZHAO Xichun. Research on the appraisal method of missile impact accuracy[J]. Modern Defence Technology, 2008, 36(3): 33–36. |
| [7] |
EFRON B B.
Bootstrap Methods:Another Look at the Jackknife[J]. The Annals of Statistics, 1979, 7(1): 1–26.
DOI:10.1214/aos/1176344552
|
| [8] |
茆诗松.
贝叶斯统计[M]. 北京: 中国统计出版社, 2012.
|
| [9] |
陈希孺.
数理统计学教程[M]. 北京: 中国科技大学出版社, 2009.
|
| [10] |
孟昭为.
二项分布参数的置信区间[J]. 大学数学, 1995(4): 169–171.
MENG Zhaowei. Confidence interval of parameter for binomial distribution[J]. Journal of Mathematics for Technology, 1995(4): 169–171. |
 2018, Vol. 50
2018, Vol. 50


