雷达的测量误差分为系统误差(设备系统误差、测量误差)、随机误差和过失误差，设备系统误差包括零值误差、大盘不水平、光机轴偏差、两轴不正交误差等^[1-2]。其中零值误差需要进行经常性的动态标定，特别是在雷达进场安装调试后和执行大型任务前必须进行雷达精度鉴定，验证和标定设备的随机误差和零值偏差。

当前雷达精度鉴定主要有四种方法^[3]：跟踪搭载全球定位系统(Global positioning system, GPS)接收机的飞机的校飞方法、跟踪卫星激光测距(Satellite laser ranging，SLR)卫星的方法^[4-5]、基于精密设备测量的方法和基于广播式自动相关监视(Automatic dependent surveillance-broadcast，ADS-B)数据的方法^[6-7]。这4种方法无一例外都是硬比方法^[8]，即把得到雷达探测数据和标准设备给出的数据进行比对，在距离、方位角和俯仰角等的一次差的基础上进行统计、分析，从而得到被试雷达的探测精度。硬比方法难以避免工作周期长、协调难度大等多种问题。

20世纪60、70年代，美国为分析民兵导弹出现的问题，花费大量人力物力提升地基雷达的测量精度，重点分析雷达的各类误差因素，建立雷达误差模型，研究雷达精度鉴定方法^[9]。前期提出了基于误差模型的最佳弹道估计(Error modei best estimate trajectory，EMBET)的跟星自鉴定技术，当时GPS卫星系统不够成熟，地球引力场模型、地球运动模型都不够精准，该技术实现起来难度较大。后来，美国发射了测地卫星(Geodetic earth orbiting satellite，GEOS)系列服务于雷达精度鉴定，解决了雷达精度鉴定的难题，满足了当时的需要。

随着空间卫星数量的增加，地球引力场模型、地球运动模型越来越准确，笔者认为继续发展雷达跟星自鉴定技术已经具备了基础条件。目前航天活动的日益频繁，继续研究地基雷达跟星自鉴定技术仍然有重大现实意义，该技术可以使雷达精度鉴定更加快速灵活，更加自主可控。

本文介绍前期研究雷达跟星自鉴定技术的阶段成果，给出了一套雷达跟踪卫星后快速给出雷达零值的方法。

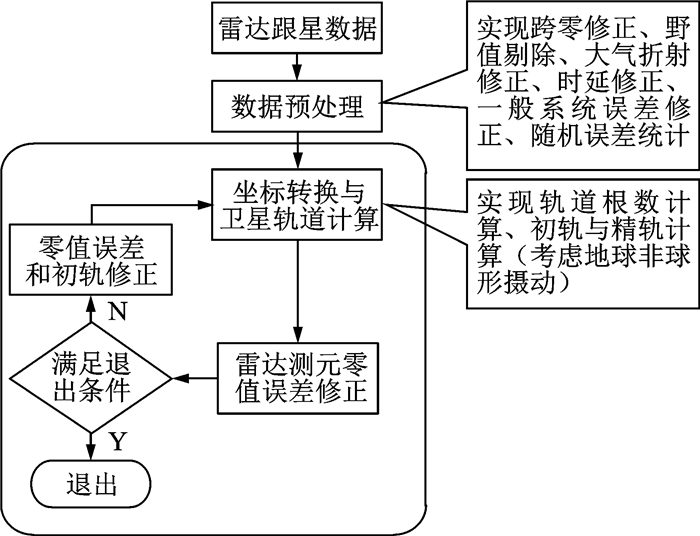
1 地基雷达跟星自鉴定技术方案

实现雷达跟星自鉴定的前提是卫星自由飞行，跟星期间没有进行轨道调整，而且卫星体积不能太大且属于中低轨卫星。用雷达跟星测量数据实现测元零值误差估计的基本流程如图 1所示。

首先，进行数据预处理，包括方位角跨零修正、野值剔除、大气折射修正、时延修正、一般系统误差修正、随机误差统计。然后，实现循环迭代估计雷达测元零值误差。

1.1 数据预处理

(1) 方位角跨零修正^[10]

当卫星由雷达Ⅰ象限向Ⅳ象限或者从相反方向移动时(以测站水平面内的天文北作为零度，顺时针方向旋转为正)，每次雷达所测量的方位角A值会出现跨零跳跃，为使测量值连续必须进行修正，消除跨零跳跃问题。

(2) 随机误差统计

统计雷达的随机误差是为了了解和掌握雷达的测量性能，看其是否满足精度设计指标要求，利于分析、检查设备各环节的问题和原因，帮助改进雷达系统设计。另外统计随机误差也是外测数据处理的依据，对测量数据野值的判断标准就是以随机误差为依据的。

(3) 野值检测与替换

野值又称异常值，雷达测量数据出现野值的原因很多，包括设备故障或者数据传输和记录过程出现异常，周围环境的突发性变化和干扰，以及操作人员的过失等。测量数据含有野值使测量值严重失真，降低了观测数据的置信度，势必影响数据处理结果的精度。因此数据处理时，必须首先对观测数据的异常值进行判别和处理，以合理、可信的数据替代它，保证外测数据处理结果的质量。

(4) 系统误差修正

测量数据的系统误差主要来自设备、跟踪和参数误差3个方面。对单脉冲雷达而言，设备误差包括测距与测角系统固定偏差、三轴不正交、天线畸变、传感器非线性、基座倾斜、零点漂移、伺服不平衡、天线偏倚、动态滞后等；跟踪误差包括瞄准误差、时统误差、电波折射、传播时延等；参数误差包括光速误差、振荡器频率误差、大地坐标误差等。雷达测元零值误差估计^[11]前需要尽可能地消除已知系统误差的影响。

(5) 时间误差修正

时间误差包括来自时统设备的时间误差、时统设备与雷达设备测量点上时间不同步误差、电波传播时延误差。不同步误差通常为固定值、电波时延误差是一个与目标距离相关的变化误差。

(6) 大气折射修正

测量空间各处大气成分、密度、湿度和电离程度不相同，介质特性相当复杂，因此电波和光波通过大气传播时，其传播速度已不是匀速直线运动，路径也发生弯曲，这就引起电波(或光波)信号的折射误差。电波(光波)折射是影响外测数据测量精度的重要误差源，在雷达数据处理时必须进行修正处理^[12]。

(7) 低仰角数据切除

雷达低仰角测量时受到多径效应、对流层和电离层折射较为严重且复杂，因此低仰角测量数据在精确处理时有必要进行切除。

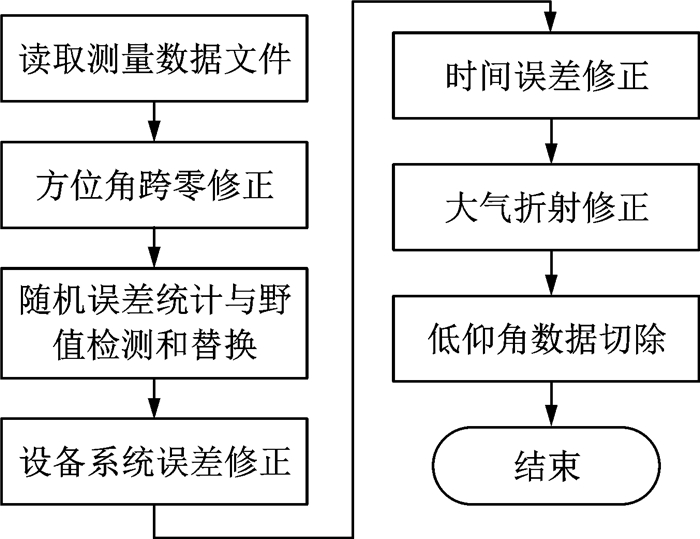
整个数据预处理的流程如图 2所示。

1.2 测元零值误差估计

测元零值误差估计涉及的理论基础主要有三条：一是二体轨道理论，可以采用某时刻的位置和速度量表示任意时刻卫星的位置和速度^[13]；二是轨道积分理论，已知某时刻目标在空间的位置和速度可以唯一确定目标轨道，而这个唯一轨道可以通过轨道积分理论进行准确预报；三是最小二乘法参数估计理论。

(1) 二体轨道理论

卫星绕地球运动的轨道是很复杂的，它要受到地球引力、大气阻力、日月引力、太阳辐射压力等力的作用。但运动的基本情况还是把卫星看成质点，它绕一个均匀球形地球的运动，这就是天体力学中的最基本“二体运动”，其它作用力包括地球非球形部分的引力作用都可以看作“摄动力”。二体问题在数学上是完全可解的，二体运动可以看成卫星的近似运动，一般在初始轨道确定、卫星观测预报，在一定范围内都把卫星轨道看成椭圆。二体运动遵守开普勒定律。

(2) 轨道积分理论

给定任意时刻卫星的状态(位置和速度)，可以得到相应时刻卫星的摄动力，从而确定卫星瞬时的受力情况，采用常微分方程数值积分方法可以求解下一时刻卫星的状态。常用的积分方法有Cowell法、Encke法^[14]、Runge-Kutta法^[15]、Adams预测校准法等，本文采用Runge-Kutta-Fehlberg法和Adams预测校准法。

(3) 参数估计理论

参数估计理论和方法是外测数据处理的重要数学基础，外测数据处理中经常使用的参数估计方法包括矩估计、最大似然估计和最小二乘估计。最小二乘估计最早形式是高斯估计，适用于随机误差为等方差不相关条件，对于随机误差变化的测量数据序列需要采用马尔科夫估计。本文采用马尔科夫估计实现测元零值误差的估计。

2 雷达测元零值估计方法 2.1 即时惯性坐标系

一般在地心惯性坐标系下分析卫星轨道，常用的坐标系为J2000坐标系，但是从地心固定坐标系(Earth-centered fixed coordinates，ECF)转到J2000坐标系过程复杂，因此本文提出一种即时惯性坐标系，即以某时刻T₀为起始时刻，对该时刻的地心固定坐标系，通过极移变换后，转到准地固坐标系，以该时刻的准地固坐标系为基准，建立瞬时惯性坐标系，坐标系不再随地球旋转，称该惯性坐标系为即时惯性坐标系。

2.2 观测方程建立

当t_j时刻观测方程数据为距离R_j、俯仰角E_j、方位角A_j时，得到轨道在测站坐标系中的位置坐标为

$ \left\{ \begin{array}{l} {x_j} = {R_j}\cos {E_j}\cos {A_j}\\ {y_j} = {R_j}\sin {E_j}\\ {z_j} = {R_j}\cos {E_j}\sin {A_j} \end{array} \right. $

得到对应即时惯性坐标系下的坐标为

$ {\mathit{\boldsymbol{X}}_j} = \mathit{\boldsymbol{\theta }}_j^{\rm{T}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{R}}_{\lambda \varphi }}{\mathit{\boldsymbol{x}}_j} + {\mathit{\boldsymbol{X}}_{G0}}} \right) $

式中，${\mathit{\boldsymbol{X}}_j} = {\left[ {{X_j}\;\;{Y_j}\;\;{Z_j}} \right]^{\rm{T}}}, {\mathit{\boldsymbol{x}}_j} = {\left[ {{x_j}\;\;{y_j}\;\;{z_j}} \right]^{\rm{T}}}, {\mathit{\boldsymbol{\theta }}_j} $是即时惯性坐标系向准地固坐标系的旋转矩阵，P是准地固坐标系向地固坐标系的旋转矩阵，R_λφ是测量系向地心固定坐标系的旋转矩阵，X_G0是雷达站点在地心固定坐标系下的坐标。

记$ {\mathit{\boldsymbol{X}}_0} = {\left[ {{X_0}\;\;{Y_0}\;\;{Z_0}\;\;{{\dot X}_0}\;\;{{\dot Y}_0}\;\;{{\dot Z}_0}} \right]^{\rm{T}}}$为卫星在T₀时刻在即时惯性坐标系下的坐标，根据卫星二体力学条件，建立任意时刻卫星坐标X_j与X₀的关系。

$ {\mathit{\boldsymbol{X}}_j} = {\mathit{\boldsymbol{G}}_j}{\mathit{\boldsymbol{X}}_0} $

式中

$ {\mathit{\boldsymbol{G}}_j} = \left[ {\begin{array}{*{20}{c}} {{f_j}}&0&0&{{g_j}}&0&0\\ 0&{{f_j}}&0&0&{{g_j}}&0\\ 0&0&{{f_j}}&0&0&{{g_j}} \end{array}} \right] $

式中

$ {f_j} = 1 - \frac{a}{{{r_0}}}\left( {1 - \cos \Delta {E_j}} \right) $

$ {g_j} = \Delta {t_j} - \frac{1}{n}\left( {\Delta {E_j} - \sin \Delta {E_j}} \right) $

式中a是轨道长半轴，r₀是T₀时刻目标的地心距，Δt_j=t_j－T₀，ΔE_j=E_j－E₀。各轨道参数的解算方法参考二体轨道理论部分。

令${\mathit{\boldsymbol{F}}_j} = {\rm{ }}\mathit{\boldsymbol{R}}_{\lambda \varphi }^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\theta }}_j} $，可以建立任意时刻测量量x_j与X₀的关系。

$ {\mathit{\boldsymbol{x}}_j} + \mathit{\boldsymbol{R}}_{\lambda \varphi }^{\rm{T}}{\mathit{\boldsymbol{X}}_{G0}} = {\mathit{\boldsymbol{F}}_j}{\mathit{\boldsymbol{G}}_j}{\mathit{\boldsymbol{X}}_0} $

2.3 误差关系式建立

记雷达零值误差量为R₀、E₀、A₀，则在测量坐标系中观测数据的误差为

$ \Delta {\mathit{\boldsymbol{X}}_j} = {\mathit{\boldsymbol{L}}_j} \cdot \mathit{\boldsymbol{C}} $

其中

$ {\mathit{\boldsymbol{L}}_j} = \left[ {\begin{array}{*{20}{c}} {\cos {A_j}\cos {E_j}}&{ - {R_j}\cos {A_j}\sin {E_j}}&{ - {R_j}\sin {A_j}\cos {E_j}}\\ {\sin {E_j}}&{{R_j}\cos {E_j}}&0\\ {\sin {A_j}\cos {E_j}}&{ - {R_j}\sin {A_j}\sin {E_j}}&{{R_j}\cos {A_j}\sin {E_j}} \end{array}} \right] $

$ \mathit{\boldsymbol{C}} = {\left[ {\begin{array}{*{20}{c}} {{R_0}}&{{E_0}}&{{A_0}} \end{array}} \right]^{\rm{T}}} $

考虑到随机误差(记为η_j)，则测站坐标系下的误差向量为

$ \Delta {\mathit{\boldsymbol{X}}_j} = {\mathit{\boldsymbol{L}}_j} \cdot \left( {\mathit{\boldsymbol{C}} + {\mathit{\boldsymbol{\eta }}_j}} \right) $

从而得到

$ {\mathit{\boldsymbol{x}}_j} + \mathit{\boldsymbol{R}}_{\lambda \varphi }^{\rm{T}}{\mathit{\boldsymbol{X}}_{G0}} = {\mathit{\boldsymbol{F}}_j}{\mathit{\boldsymbol{G}}_j}{\mathit{\boldsymbol{X}}_0} + {\mathit{\boldsymbol{L}}_j}\mathit{\boldsymbol{C}} + {\mathit{\boldsymbol{L}}_j}{\mathit{\boldsymbol{\eta }}_j} $

2.4 测元零值误差估计

进一步转换成高斯-马尔科夫估计所需形式为

$ {\mathit{\boldsymbol{x}}_j} + \mathit{\boldsymbol{R}}_{\lambda \delta }^{\rm{T}}{\mathit{\boldsymbol{X}}_{G0}} = \left[ {{\mathit{\boldsymbol{F}}_j}{\mathit{\boldsymbol{G}}_j}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_0}}\\ \mathit{\boldsymbol{C}} \end{array}} \right] + {\mathit{\boldsymbol{L}}_j}{\mathit{\boldsymbol{\eta }}_j} $

记$\mathit{\boldsymbol{Y}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{X}}_0}\\ \mathit{\boldsymbol{C}} \end{array} \right], \mathit{\boldsymbol{F}} = \left[ {{\mathit{\boldsymbol{F}}_j}{\mathit{\boldsymbol{G}}_j}\;\;{\mathit{\boldsymbol{L}}_j}} \right], \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{x}}_j} + \mathit{\boldsymbol{R}}_{\lambda \varphi }^{\rm{T}}{\mathit{\boldsymbol{X}}_{G0}}, \mathit{\boldsymbol{\eta }} = {\mathit{\boldsymbol{L}}_j}{\mathit{\boldsymbol{\eta }}_j} $，则上式可以写为

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{Y}} + \mathit{\boldsymbol{\eta }} $

则

$ \mathit{\boldsymbol{\hat Y}} = {\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{F}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{y}} $

利用分块矩阵求逆的方法，可以将$ \left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{F}}} \right)$表示成

$ {\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{11}}}&{{\mathit{\boldsymbol{M}}_{12}}}\\ {{\mathit{\boldsymbol{M}}_{21}}}&{{\mathit{\boldsymbol{M}}_{22}}} \end{array}} \right] $

可以将${\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{y}} $表示成

$ {\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_X}}\\ {{\mathit{\boldsymbol{M}}_C}} \end{array}} \right] $

从而求的X₀和C

$ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_0}}\\ {\mathit{\boldsymbol{\hat C}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{{{\hat X}_0}}}}&{{\mathit{\boldsymbol{P}}_{{{\hat X}_0}\hat C}}}\\ {{\mathit{\boldsymbol{P}}_{\hat C{{\hat X}_0}}}}&{{\mathit{\boldsymbol{P}}_{\hat C}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_X}}\\ {{\mathit{\boldsymbol{M}}_C}} \end{array}} \right] $

式中

$ {\mathit{\boldsymbol{P}}_{\hat C}} = {\left[ {{\mathit{\boldsymbol{M}}_{22}} - {\mathit{\boldsymbol{M}}_{21}}\mathit{\boldsymbol{M}}_{11}^{ - 1}{\mathit{\boldsymbol{M}}_{12}}} \right]^{ - 1}} $

$ {\mathit{\boldsymbol{P}}_{{{\hat X}_0}}} = \mathit{\boldsymbol{M}}_{11}^{ - 1} + \mathit{\boldsymbol{M}}_{11}^{ - 1}{\mathit{\boldsymbol{M}}_{12}}{\mathit{\boldsymbol{P}}_{\hat C}}{\mathit{\boldsymbol{M}}_{21}}\mathit{\boldsymbol{M}}_{11}^{ - 1} $

$ {\mathit{\boldsymbol{P}}_{{{\hat X}_0}\hat C}} = - \mathit{\boldsymbol{M}}_{11}^{ - 1}{\mathit{\boldsymbol{M}}_{12}}{\mathit{\boldsymbol{P}}_{\hat C}} $

$ {\mathit{\boldsymbol{P}}_{C{X_0}}} = {\mathit{\boldsymbol{P}}_{{X_0}C}}^{\rm{T}} $

则

$ \mathit{\boldsymbol{\hat C}} = {\mathit{\boldsymbol{P}}_{\hat C}}\left[ {{\mathit{\boldsymbol{M}}_C} - {\mathit{\boldsymbol{M}}_{21}}\mathit{\boldsymbol{M}}_{11}^{ - 1}{\mathit{\boldsymbol{M}}_X}} \right] $

$ {{\mathit{\boldsymbol{\hat X}}}_0} = {\mathit{\boldsymbol{P}}_{{{\hat X}_0}}} \cdot {\mathit{\boldsymbol{M}}_X} + {\mathit{\boldsymbol{P}}_{{{\hat X}_0}\hat C}} \cdot {\mathit{\boldsymbol{M}}_C} $

3 方法验证 3.1 验证流程

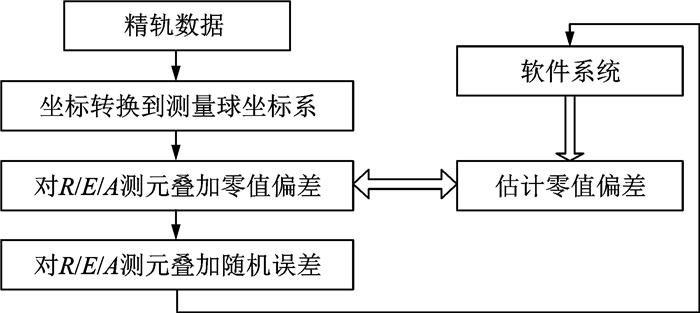
根据前面的方法开发了软件，采用设定参数模拟测量数据，然后采用本文方法估计设定的参数进行验证。首先将卫星精轨数据转换到给定雷达测量球坐标系，然后对三个测元叠加零值偏差，最后叠加随机误差。采用模拟的测量数据输入软件系统，估计指定雷达的测元零值，把估计结果与预设3个测元零值比较。方法验证流程如图 3所示。

3.2 验证结果

(1) 无噪声仿真验证结果

以单雷达跟踪卫星一个弧段的数据进行验证，三次验证情况见表 1。

可以看出估计误差最大的是第1次验证实验，距离零值估计误差约0.1 m，俯仰角零值估计误差约5E-4 mrad，方位角估计误差约1.62E-2 mrad。经分析零值误差估计残差是由精轨自身精度、轨道积分方法、以及计算机截断误差等因素带来。验证结果表明本文提出的准实时精度验证方法正确有效。

(2) 有噪声仿真验证结果

雷达测量过程中存在随机误差，在测量数据模拟时为三个测元分别叠加了方差为5 m、0.14 mrad、0.14 mrad的随机误差。验证结果表明俯仰角零值估计误差 < 0.01 mrad，精度较高；而在距离零值和方位零值方面估计误差较大，其中距离零值估计误差 < 50 m、方位角零值估计误差 <0.5 mrad。

经过深入分析多次仿真结果，得出如下结论：

(1) 俯仰角零值估计最准。因为俯仰角偏差受轨道高度和周期的约束，因此估计精度最高。

(2) 距离零值估计较方位角零值估计准确。距离零值受轨道形状的约束，比如轨道偏心率，因此估计精度较俯仰角零值估计精度差，而较方位角零值估计精度好。

(3) 方位角零值估计效果最差。因为方位角偏差主要表现为轨道的平移，对轨道形状影响较小。

(4) 随机误差与估计轨道参数的耦合效应，造成单雷达单弧段精度验证效果差。

4 结束语

为了克服随机误差对估计精度的影响，提高误差估计精度，提出了3种新的估计模式：单雷达单星双弧段模式、单雷达多星多弧段模式和多雷达联合跟星模式，取得了较好的效果，将在后续研究中深入探讨。