2. 中国航天空气动力技术研究院, 北京, 100074
2. China Academy of Aerospace Aerodynamics, Beijing, 100074, China
飞行器在飞行过程中的噪声来源主要有两个:一是发动机引起的喷流噪声;二是飞行器与大气相互作用产生的脉动压力环境所引起的气动噪声[1]。
强烈的噪声环境对飞行仪器、结构和人员都有不利的影响。当声压级达到140 dB时,一般的飞行仪器就不能正常工作;对于载人飞行器,当飞行器内部的声压级达到120 dB时,人员会感到很难受。另外,脉动压力也会引起很大的局部载荷,尤其是与低阶模态的频率范围接近时,脉动压力的低频成份会引起结构的抖振响应。在航空航天发展史上,因脉动压力造成的事故时有发生。美国的登月火箭在跨声速飞行时由于脉动压力造成过火箭头部整流罩破坏;发射“水星”MA-3飞船时也因跨声速下的脉动压力引起结构振动,部件失效从而导致发射失败;“阿波罗”飞船再入返回途中,在10 km高空附近由脉动压力所产生的强烈噪声致使宇航员没有听到指挥中心指令,从而导致严重后果[2]。可见,飞行器脉动压力的研究不容忽视。
脉动压力与飞行器的外形、飞行马赫数、动压以及攻角等参数密切相关。在飞行器外形过渡处、舱段连接处、整流罩、空腔和突起等部位非常容易产生脉动压力。脉动压力的产生机制主要是来流和边界层的转捩/湍流特性、绕流分离/再附特性和激波振荡特性这些局部复杂的流动特性[3]。
对于附体流,表面脉动压力由边界层的特性决定,对层流区,不产生脉动压力;在湍流区,它的强弱取决于流态、物形和表面粗糙度等因素;在转捩区,它存在峰值,因此可利用此特性,判断边界层转捩区。
当飞行器表面产生强的逆压梯度时,可能导致气流分离,在分离区,其复杂的分离流动结构使得飞行器表面会产生强于湍流边界层产生的脉动压力,并在分离与再附点处出现峰值。
在飞行器表面,当局部流动达到声速时,形成局部超声速区并伴随生成激波。此时,激波往往是极不稳定的,弱激波与边界层相互作用,引起绕流分离和再附位置发生波动,形成激波振荡。加之气流分离和再附的交替出现,会产生强烈的随机脉动压力,甚至引起结构振动[4]。
目前常用的脉动压力预示方法主要有风洞试验、经验公式和数值模拟。对数值模拟脉动压力来说,需要准确、成熟的高雷诺数非定常模拟方法。大量的测量和飞行试验表明,脉动压力的频率范围很广,从几赫兹到几千赫兹,这要求数值模拟的时间步长应该尽可能小同时统计时间应该尽可能长,这使得计算的开销特别大。另一方面,复杂外形的脉动压力往往是由复杂的流动特征引发的,例如大分离、剪切层不稳定、涡干扰等,对这些复杂的流动现象的准确模拟到目前为止仍然是计算流体力学所面临的一项重要挑战,准确获得脉动压力的前提是准确捕获复杂流动特征的时均量和瞬时量。大涡模拟(Large eddy simulation, LES)通过模化小尺度涡,直接计算大尺度非定常分离流动在针对复杂流动现象的模拟上体现出明显的优势,然而对高雷诺数流动的苛刻网格要求,尚不完全成熟的近壁面模化方法严重地制约了LES在工程实际中的应用。近年来,综合雷诺平均NS方程(Reynolds average Navier-Stokes, RANS)和LES各自的优点,兴起了多种RANS-LES混合方法。这些方法的共同思想是采用RANS高效可靠地模拟高频小尺度运动占主导地位的近壁区域,同时采用LES准确计算低频大尺度运动占优的非定常分离流动区域。RANS-LES混合方法是当前有限计算资源条件下处理高雷诺数大分离流动的合理选择,已经在多种流动类型的模拟中得到广泛的应用,获得了很多有价值的研究成果。在对脉动压力的研究中,越来越多的研究者开始使用RANS-LES混合方法研究脉动压力问题[5-13]。
针对可重复使用飞行器在竖立状态、跨声速飞行、超声速飞行等几种典型状态下的脉动压力问题,本文采用RANS-LES混合方法进行了研究。
1 数值模拟方法本文采用RANS-LES混合方法中的分离涡模拟(Detached eddy simulation,DES)类方法进行数值模拟,选取的混合方法为基于SST湍流模型的延迟分离涡模拟方法DDES(Delayed detached eddy simulation,DDES)[14-20]。
1.1 DES/DDES方法构造DES/DDES混合方法基于传统的RANS湍流模型方程构造而来。本项目采用基于Menter k-ω SST湍流模型的混合方法。Menter k-ω SST两方程湍流模型(SST)为
| $ \left\{ \begin{array}{l} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (\rho {u_j}k)}}{{\partial {x_{j}}}} = P - {\beta ^*}\rho \omega k{\rm{ }} + \\ \;\;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial {x_{j}}}}\left[ {(\mu {\rm{ }} + {\rm{ }}{\sigma _{k}}{\mu _{t}})\frac{{\partial k}}{{\partial {x_j}}}} \right]\\ \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial (\rho {u_j}\omega )}}{{\partial {x_j}}} = {\rm{ }}\frac{\gamma }{{{\nu _t}}}P - {\beta ^*}\rho {\omega ^2} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + } \right.} \right.\\ \;\;\;\;\;\;\;{\sigma _{\omega }}{\mu _{t}})\frac{{\partial \omega }}{{\partial {x_j}}} + 2(1 - {F_{1}})\frac{{\rho {\sigma _{\omega 2}}}}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}} \end{array} \right. $ | (1) |
将RANS湍流模型中的长度尺度使用DES的长度尺度代替,就获得了基于该湍流模型的DES混合方法。DES的长度尺度由RANS和LES的长度尺度以如下方式混合得到
| $ {l_{{\rm{DES}}}} = {\rm{min}}({l_{{\rm{RANS}}}}, \;{l_{{\rm{LES}}}}) $ | (2) |
其中LES长度尺度仅由网格间距得到
| $ {l_{{\rm{LES}}}} = {C_{{\rm{DES}}}}\Delta $ | (3) |
式中Δ为局部网格间距。
SST湍流模型的RANS长度尺度为
| $ {l_{{\rm{RANS}}}} = \frac{{{k^{\frac{1}{2}}}}}{{{\beta ^*}\omega }} $ | (4) |
采用式(4),SST两方程湍流模型k方程的湮灭源项β*ρωk可重新写为
| $ {\beta ^*}\rho \omega k = \frac{{\rho {k^{\frac{3}{2}}}}}{{{l_{{\rm{RANS}}}}}} $ | (5) |
将湍流模型中的lRANS用lDES代替,就得到了基于该湍流模型的DES混合方法。
CDES是一个需要经过标定和验证的经验常数,反映了不同计算流体力学代码的耗散程度,本文直接取模型开发者标定的数值。对基于SST模型的DES方法,由于原始的SST模型本身是一个两层模型,外层是k-ε模型,内层是k-ω模型,因此CDES也应该采取SST模型的构造方法进行混合
| $ {C_{{\rm{DES}}}} = (1 - {F_1})C_{{\rm{DES}}}^{{\rm{outer}}} + {F_1}C_{{\rm{DES}}}^{{\rm{inner}}} $ | (6) |
式中CDESouter取0.61,CDESinner取0.78。F1是SST模型的内部函数。
从DES模型的构造过程可见,在RANS长度尺度占主导时,模型以传统RANS湍流模型的方式计算,在LES长度尺度占主导时,湍流模型的行为表现为经典的Smagorisnky亚格子模型,从而实现了RANS-LES以统一方式进行混合计算。
DES方法对RANS区域和LES区域的划分仅依赖于网格尺度。这在某些情况可能会出现以下的问题:随着网格的加密,LES计算可能会在边界层内被激活,但此时网格的密度并不足以提供LES计算湍流边界层所需要的网格密度,这使得LES产生过小的湍流粘性,产生模化应力损耗(Modeled stress depletion, MSD),MSD的直接后果是导致网格诱导的分离(Grid induced seperation, GIS)。为了尽可能避免MSD和GIS,经典的DES对网格拓扑和分布提出了很高的要求。
DDES方法通过引入一个延迟函数,重新构造了DDES的长度尺度lDDES,极大程度上避免了MSD问题,本文的RANS-LES混合方法即采用了DDES方法。
与DES方法类似,使用DDES的长度尺度lDDES代替湍流模型中长度尺度lRANS,即获得了基于原始湍流模型的DDES方法,其长度尺度lDDES可表示为
| $ {l_{{\rm{DDES}}}}{\rm{ = }}{l_{{\rm{RANS}}}} - {f_{\rm{d}}}{\rm{max}}\left\{ {{\rm{0, }}\;{l_{{\rm{RANS}}}} - {l_{{\rm{LES}}}}} \right\} $ | (7) |
延迟函数fd定义如下
| $ {f_{\rm{d}}} = 1 - \tanh \left[ {{{({c_{\rm{d}}}{r_{\rm{d}}})}^3}} \right] $ | (8) |
rd的表达式如下
| $ {r_{\rm{d}}} = \frac{{\nu + {\nu _{\rm{t}}}}}{{\sqrt {{u_{i, j}}{u_{i, j}}} {\kappa ^2}{d^2}}} $ | (9) |
式中:ν为摩尔黏性,νt为湍流黏性,ui, j为速度梯度,d是到最近壁面的距离,κ为Karman常数取0.41,实验常数cd取8。
从DDES的构造可见,当fd趋于0时,采用RANS计算,而当fd趋于1时,转化为传统的DES方法。通过这个方法保护了在附着流边界层的RANS区域计算,而不会影响在其他区域的DES计算。
1.2 其他用到的数值方法计算采用格心格式的非结构有限体积法,Roe格式计算无粘通量,反距离权重最小二乘法计算单元内的梯度分布以获得二阶空间精度,Venkatakrishnan限制器抑制间断附近的过冲和振荡。
脉动压力的计算模拟都是非定常的,非定常采用双时间步方法计算,物理时间层采用二阶向后差分,伪时间层采用LU-SGS隐式时间推进。
基于可压缩流动的求解器不适合计算低速流动,为此采用针对时间导数的当地预处理方法,不仅能很好地消除低速时控制方程刚性太大导致的计算精度和计算效率下降问题,而且在高速时能自然地恢复到无预处理状态,特别适合竖立风载计算时高低速流动并存时尺度不一致问题。
2 计算网格DDES方法对网格质量的要求比RANS要高。本文采用多区结构网格,飞行器的物面附近采用O型网格,远离物面采用H型网格。物面附近附面层内的O型网格用来保证物面的正交性和物面法向密度。物面附近的网格进行了加密,以确保壁面的y+ < 1。此外,在流动可能的分离处、强逆压梯度位置的网格也进行了加密以捕获更丰富的流动现象。总网格数超过2 000万个。选取的物理时间步长为5e-4 s。总共计算了10 s,取2 s之后的数据进行统计。
3 典型状态下的脉动压力计算 3.1 竖立状态下的脉动压力计算对于垂直发射的飞行器而言,竖立在发射台上时,地面风是影响飞行器结构和控制系统设计的重要环境因素。目前国内对风载荷的研究主要集中在火箭或导弹发射过程中,研究外形以简单细长旋成体为主,研究过程中可对飞行器简化为圆柱绕流问题,进而采用工程或试验的方法可以获得工程可用的风载特性[21]。但对于可重复使用飞行器这类复杂外形而言,研究开展相对较少,可参考的试验数据非常有限。本文采用的数值模拟方法不失为一种有效途径。
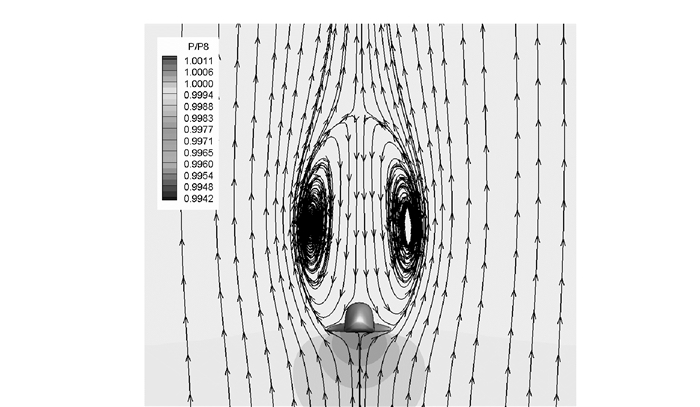
本文中,可重复使用飞行器在竖立状态下选取的计算风速为15 m/s,攻角为90°,风向角为0°,高度接近海平面。图 1,2分别给出了某x截面位置计算得到的瞬时展向涡和空间流线。从图中可见,飞行器背风面的流动结构非常丰富,是典型的旋涡主导的大分离非定常流动现象。

|
图 1 某x截面位置的瞬时展向涡 Figure 1 Instantaneous vorticity distribution of a certain transverse-section (x-axial) |
|
图 2 某x截面位置的空间流线 Figure 2 Streamlines of a certain transverse-section (x-axial) |
脉动压力均方根Prms反映了当地压力脉动的平均值。选取以下典型位置进行分析:不同x截面位置、绕翼根、背风区对称面、沿尾翼前沿、沿尾翼内侧这些位置。
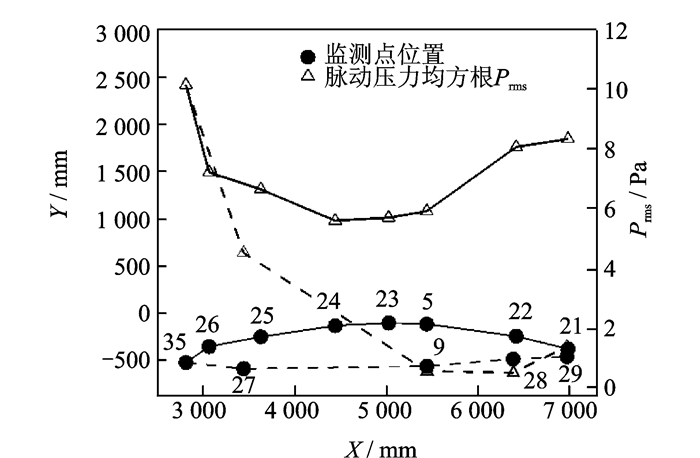
图 3给出了不同x截面处沿机体周向的脉动压力均方根。从图 3中可见,迎风面的脉动压力很小,可以忽略。在机体中部背风面脉动压力均方根小于10 Pa;在尾翼前缘机体背风区分离点附近脉动压力较强,超过40 Pa,随着向对称面靠近,脉动压力载荷迅速减小到10 Pa左右的量级。
|
图 3 不同x截面处沿机体周向的脉动压力均方根Prms Figure 3 Root-mean-square of pressure fluctuation of certain transverse-sections (variable x- locations) |
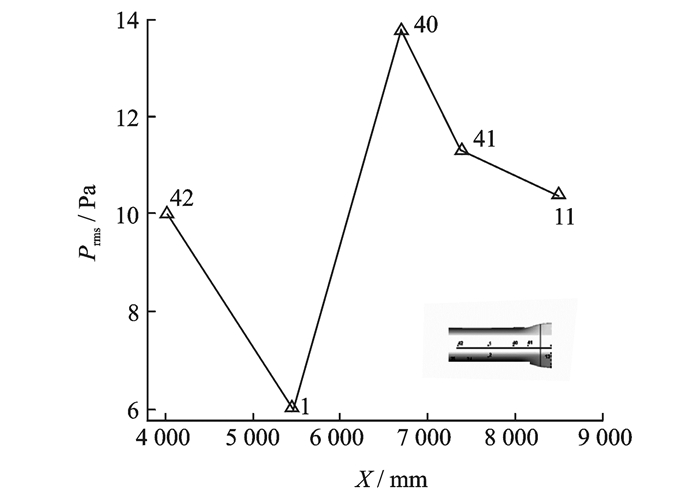
图 4给出了绕翼根一周的脉动压力均方根。从图中可见机翼根部的压力脉动都很小,背风面比迎风面要大,机翼前缘分离点处脉动最大,约为10 Pa。
|
图 4 绕翼根的一周的脉动压力均方根Prms Figure 4 Root-mean-square of pressure fluctuation at wing root cross-section |
图 5给出了机体背风区对称面上的脉动压力均方根。从图中可见机体背风区对称面上的脉动压力都很小,为10 Pa的量级。靠近翼根截面处的脉动压力略大一点。
|
图 5 背风区对称面上的脉动压力均方根Prms Figure 5 Root-mean-square of pressure fluctuation at leeward symmetry plane |
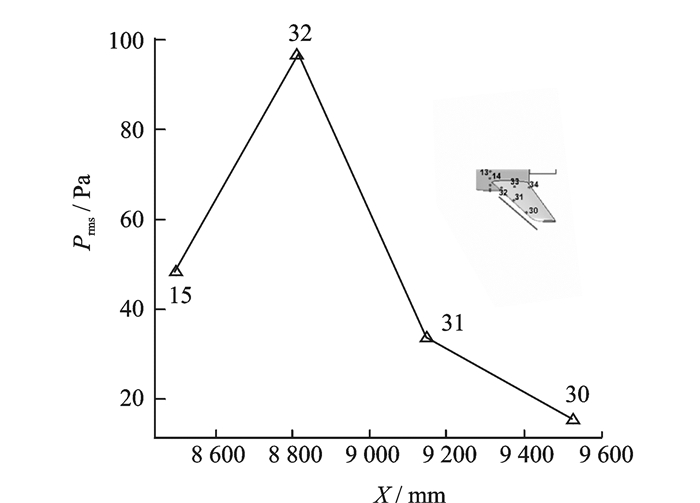
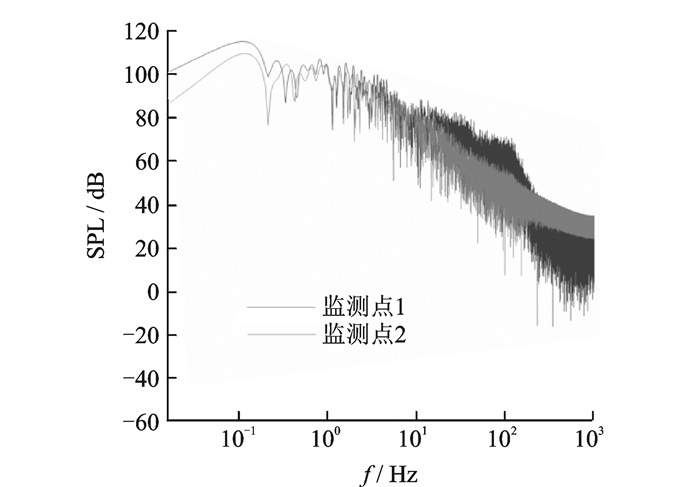
图 6给出了沿尾翼前沿的脉动压力均方根。从图中可见,尾翼前缘的脉动压力值明显比其他部位要高。在尾翼与机身较为接近的位置由于两者的相互干扰,其脉动压力明显更大,接近100 Pa。图 7为尾翼根部内侧典型监测点的声压级,最大为115 dB;脉动压力频率较低,低于1 Hz。
|
图 6 沿尾翼前沿的脉动压力均方根Prms Figure 6 Root-mean-square of pressure fluctuation at the leading edge of tail |
|
图 7 尾翼根部内侧典型监测点的声压级SPL Figure 7 Sound pressure level of typical monitoring locations embedded inward-side of the tail root |
3.2 跨声速飞行状态下的脉动压力计算
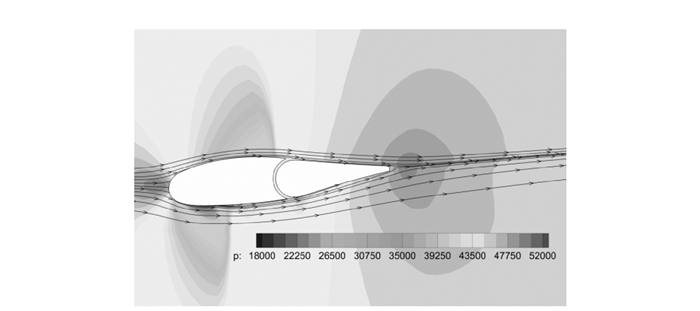
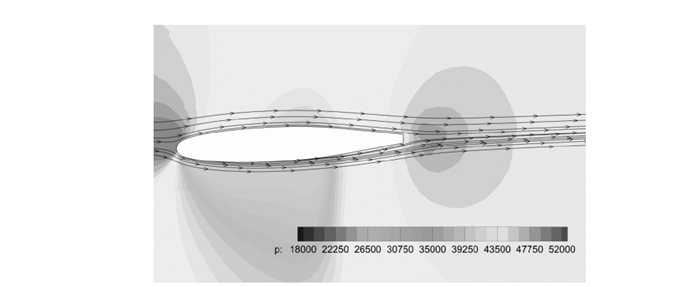
可重复使用飞行器在跨声速飞行状态下选取的计算来流马赫数为0.82,迎角为0°,飞行高度约为5 km。图 8,9分别为左机翼和左尾翼上某截面处的空间流线与压力云图。由图可见,飞行器在机翼和尾翼上出现了局部超声速区。
|
图 8 左机翼某截面的空间流场示意图 Figure 8 Streamlines and pressure distribution at a certain cross-section of the left wing |
|
图 9 左尾翼某截面的空间流场示意图 Figure 9 Streamlines and pressure distribution at a certain cross-section of the left tail |
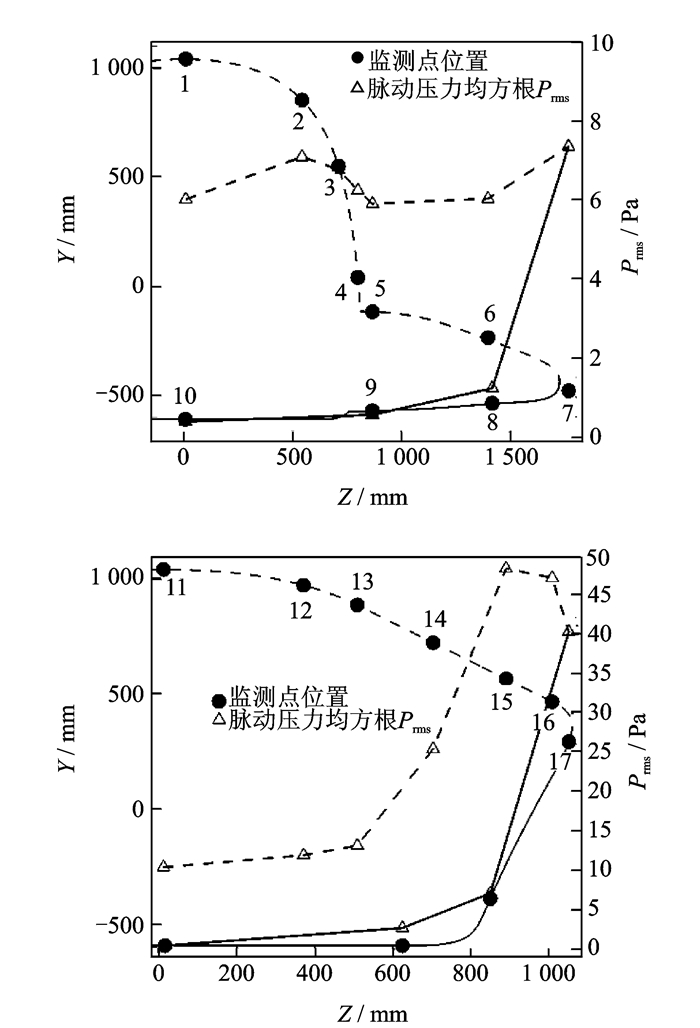
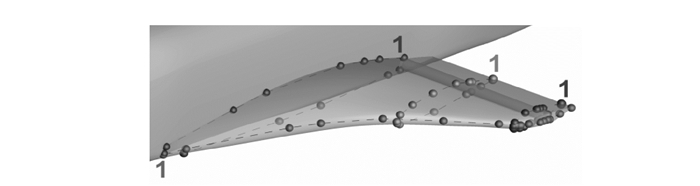
左机翼有4组监测点,见图 10。第1~3组分别沿着翼根截面、翼中截面和翼梢截面布置,起始点位置在后缘,然后经过上翼面绕到下翼面,最后回到后缘;第4组沿着机翼前缘和边缘从前往后布置。
|
图 10 左机翼监测点布置情况 Figure 10 Distribution of monitors on the left wing |
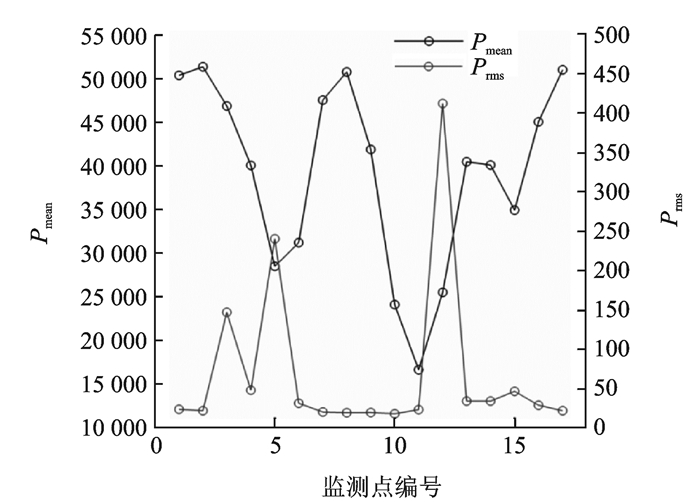
图 11给出了左机翼某截面处的脉动压力均方根Prms,从图中可见,该截面的监测点中则有几个明显的突起,表明在这些特定位置有较强的脉动压力。
|
图 11 左机翼某截面处的脉动压力均方根Prms Figure 11 Root-mean-square of pressure fluctuation at a certain cross-section of the left wing |
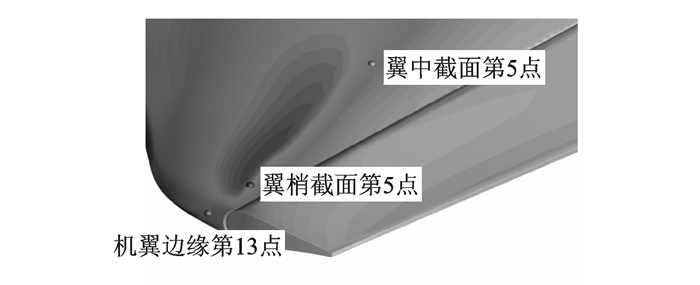
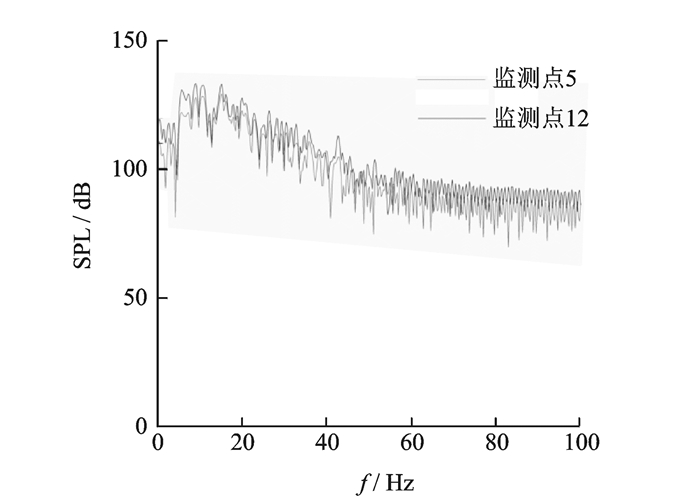
图 12给出了几个Prms较大监测点的位置。从图中可见,这几个监测点都位于激波附近,是压力梯度很大的位置。图 13给出了左机翼某截面上监测点5和监测点12的声压级SPL。从图中可见,左机翼脉动的最大强度约为137 dB。在机翼表面激波位置脉动压力的主要频率在8~15 Hz之间。
|
图 12 左机翼表面脉动压力幅度较大的位置 Figure 12 High pressure fluctuation level area on the surface of left wing |
|
图 13 左机翼某截面上监测点的声压级 Figure 13 Sound pressure level of two monitors on the left wing |
图 14为左尾翼表面压力云图及监测点位置示意图,图 15为某监测点的声压级,可达约140 dB,其主要的脉动频率约为9 Hz。

|
图 14 左尾翼表面压力云图及监测点位置 Figure 14 Pressure distribution and monitors on the left tail |

|
图 15 左尾翼某监测点的声压级 Figure 15 Sound pressure level of a monitor on the left tail |
图 16为飞行器在该计算状态下的底部流动示意图。由图可知,底部流动是一个复杂的旋涡主导的流动。该流动导致飞行器底部和体襟翼出现强烈的脉动压力。

|
图 16 飞行器的底部流动示意图 Figure 16 Demonstration of base flow field |
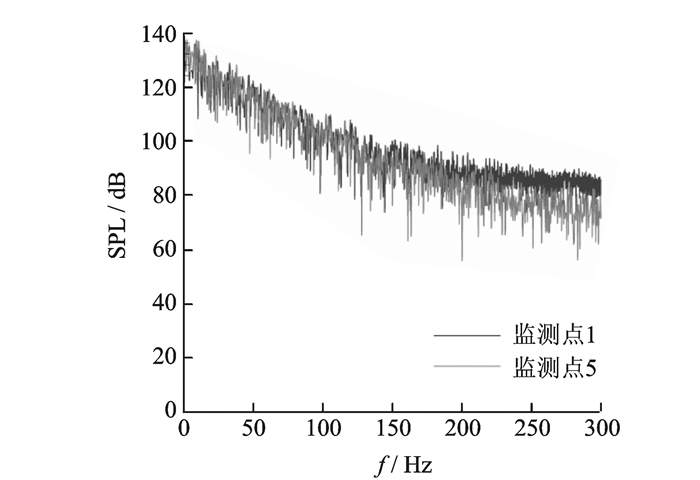
图 17为飞行器底部某监测点的声压级,可见最大声压级达到约137 dB,仅次于尾翼上的脉动强度,是飞行器脉动压力的主要来源之一。
|
图 17 飞行器底部某监测点的声压级 Figure 17 Sound pressure level of two monitors at the base |
3.3 超声速飞行状态下的脉动压力计算
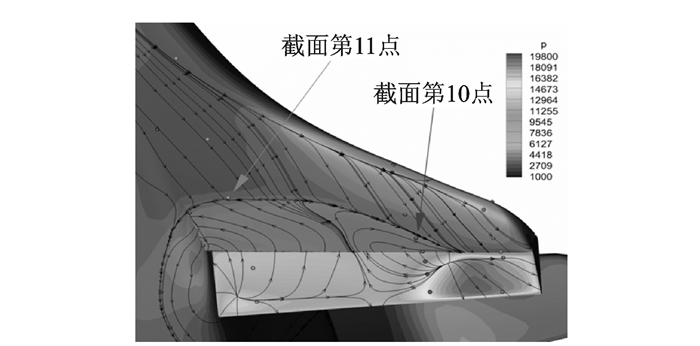
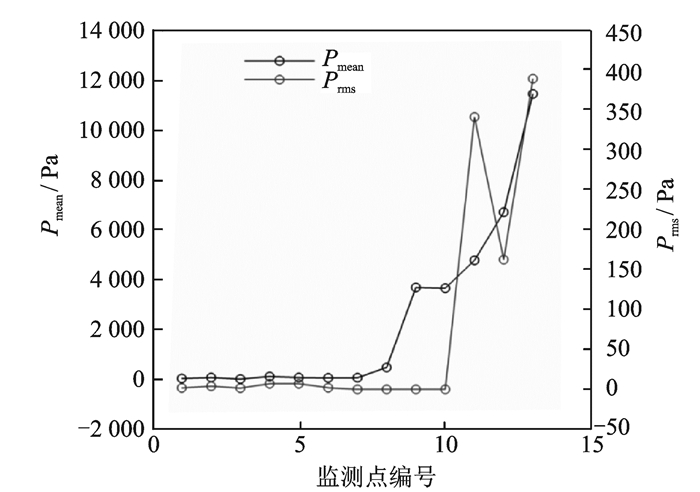
可重复使用飞行器在超声速飞行状态下选取的计算来流马赫数为3.6,迎角为26°,飞行高度约为30 km,各气动控制舵面均处于大舵偏状态,其中左副翼偏转超过25°。图 18为飞行器左机翼下表面上的流线及表面压力示意图,图 19为左机翼某截面的空间流线及压力云图,图 20为左机翼某截面处的脉动压力均方根Prms。
|
图 18 左机翼下表面上的流线及表面压力示意图 Figure 18 Streamlines and pressure distribution on the windward surface of the left wing |

|
图 19 左机翼某截面的空间流线及压力云图 Figure 19 Streamlines and pressure distribution at a certain cross-section of the left wing |
|
图 20 左机翼某截面处的脉动压力均方根Prms Figure 20 Root-mean-square of pressure fluctuation at a certain cross-section of the left wing |
由图可见,飞行器在机翼和副翼的下表面形成激波,并与机翼边界层作用导致流动分离,分离后的流动在副翼上再附,形成一个分离泡。而且该分离泡是不稳定的,随时间而变化,导致了下表面的压力脉动。
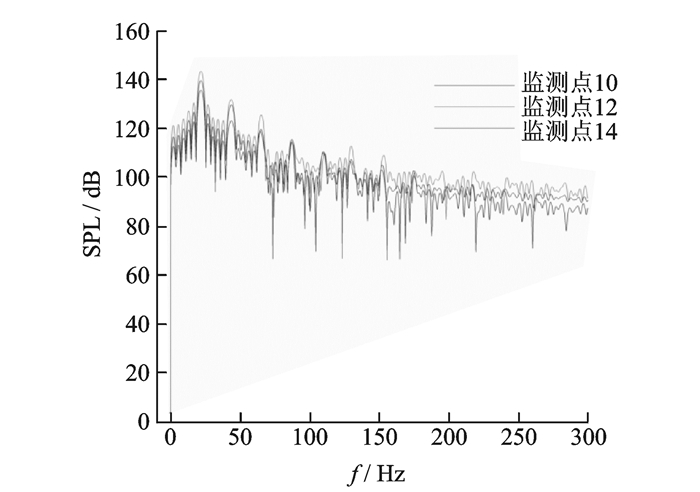
图 21给出了左机翼某截面上监测点的声压级SPL。从图中可见,左机翼脉动的最大强度约为140 dB,且强脉动的主要频率约为22 Hz。
|
图 21 左机翼某截面上监测点的声压级 Figure 21 Sound pressure level of monitors on the left wing |
4 结论
本文采用DES/DDES混合方法对可重复使用飞行器在竖立状态、跨声速飞行、超声速飞行时的脉动压力进行了数值模拟研究,经分析可得以下结论:
(1) 竖立状态下,可重复使用飞行器的脉动压力发生在背风区和分离点,强度较弱;尾翼前缘根部的脉动幅值最大达到约46 Pa,声压级可达115 dB;脉动频率很低,主频不超过1 Hz。
(2) 来流为高亚声速或接近跨声速时,可重复使用飞行器在机翼和尾翼上出现了局部超声速区。脉动压力主要是由于激波振荡产生,声压级可达约140 dB,其主要的脉动频率在10 Hz左右。
(3) 来流为超声速时,可重复使用飞行器通常处于大迎角大舵偏状态。此时,在飞行器机翼、副翼的下表面等迎风面上会出现较强的逆压梯度,使得流动发生分离,驻点、分离线和再附线附近的脉动压力较强,声压级可高达140 dB,脉动的主要频率约为22 Hz。
(4) 在飞行器底部等部位,由于物形变化,流体无法附着于物面,而产生大的流动分离,甚至会形成脱落涡,因此,也是容易产生较强脉动压力的位置。
| [1] |
ROBERTSON J E. Prediction of in-flight fluctuating pressure environments including protuberance induced flow[R]. NASA-CR-119947, WR-71-10, 71N36677, 1971. |
| [2] |
王发祥.
高速风洞试验[M]. 北京: 国防工业出版社, 2003.
|
| [3] |
黄寿康, 王玉堂.
流体力学弹道载荷环境[M]. 北京: 中国宇航出版社, 1991.
|
| [4] |
黄志澄.
航天空气动力学[M]. 北京: 中国宇航出版社, 2009.
|
| [5] |
刘振皓, 任方.
航天飞行器脉动压力数值计算方法综述[J]. 强度与环境, 2013, 40(6): 45–50.
DOI:10.3969/j.issn.1006-3919.2013.06.007 LIU Zhenhao, REN Fang. Review on numerical computation of spacecraft pressure fluctuations[J]. Structure & Environment Engineering, 2013, 40(6): 45–50. DOI:10.3969/j.issn.1006-3919.2013.06.007 |
| [6] |
BAURLE R A, TAM C J, EDWARDS J R, et al.
Hybrid simulation approach for cavity flows:Blending, algorithm, and boundary treatment Issues[J]. AIAA Journal, 2003, 41(8): 1463–1480.
DOI:10.2514/2.2129
|
| [7] |
SANCHEZ-ROCHA M, KIRTAS M, MENON S. Zonal hybrid RANS-LES method for static and oscillating airfoils and wings[R]. AIAA 2006-1256, 2006. |
| [8] |
LYNCH C E, SMITH M J. Hybrid RANS-LES turbulence models on unstructured grids[R]. AIAA 2008-3854, 2008. |
| [9] |
MENTER F R, EGOROV Y. A scale-adaptive simulation model using two-equation models[R]. AIAA 2005-1095, 2005. |
| [10] |
MENTER F R, KUNTZ M, BENDER R. A scale-adaptive simulation model for turbulent flow predictions[R]. AIAA 2003-0767, 2003. |
| [11] |
KRISHNAN V, SQUIRES K D, Forsythe J R. Prediction of the flow around a circular cylinder at high Reynolds number[R]. AIAA 2006-0901, 2006. |
| [12] |
XIAO Z X, LIU J, HUANG J B, et al.
Numerical dissipation effects on massive separation around tandem cylinders[J]. AIAA Journal, 2012, 50(5): 1119–1136.
DOI:10.2514/1.J051299
|
| [13] |
VATSA V N, LOCKARD D P. Assessment of hybrid RANS/LES turbulence models for aeroacoustics applications[R]. AIAA 2010-4001, 2010. |
| [14] |
SPALART P R.
Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 181–202.
DOI:10.1146/annurev.fluid.010908.165130
|
| [15] |
STRELETS M K. Detached eddy simulation of massively separated flows[R]. AIAA 2001-0879, 2001. |
| [16] |
SHUR M L, SPALART P R, STRELETS M K, et al.
A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638–1649.
DOI:10.1016/j.ijheatfluidflow.2008.07.001
|
| [17] |
XIAO Z X, LIU J, LUO K Y, et al.
Numerical investigation of massively separated flows past rudimentary landing gear using advanced DES approaches[J]. AIAA Journal, 2013, 51(1): 107–125.
DOI:10.2514/1.J051598
|
| [18] |
LORENZO A, VALERO E, DE-PABLO V. DES/DDES post-stall study with iced airfoil[R]. AIAA 2011-1103, 2011. |
| [19] |
DECK S. Detached-eddy simulation of transonic buffet over a supercritical airfoil[R]. AIAA 2004-5378, 2004. |
| [20] |
MORTON S.
Detached-eddy simulations of vortex breakdown over a 70-degree delta wing[J]. Journal of Aircraft, 2009, 46(3): 746–755.
DOI:10.2514/1.4659
|
| [21] |
龙乐豪.
总体设计(上)[M]. 北京: 中国宇航出版社, 1996.
|
 2018, Vol. 50
2018, Vol. 50


