空间站主动热控制系统主要通过泵驱动的单相流体回路来执行热量收集、热量传递和热量耗散3种功能。冷却工质循环至各个支路,并通过冷板或者换热器收集废热,将废热运输至中央热总线,再通过内外热控回路界面上的液-液换热器传递至外部冷却回路,最后通过外部冷却回路的辐射器向太空热沉排放。空间站热控系统的设计要求是具有较高的控温精度、可靠性和安全性,在内外热源变化较大时,具有较强的热量调控能力,使系统能够稳定运行[1-3]。机柜是空间站上为各种资源提供通用内部接口的装置,可以视为热控系统的基本单元。国际空间站标准机柜一般采用液冷结合风冷的冷却设计。EXPRESS机柜和EDR机柜设计的最大散热量均为3 000 W,其中EXPRESS机柜的最大风冷散热量设计为1 500 W,而EDR机柜的最大风冷散热设计量为1 200 W[4]。
国外文献中关于空间站热控系统设计和仿真的研究比较丰富。文献[5-9]分别介绍了国际空间站哥伦布舱、美国命运号实验舱、节点2号舱和节点3号舱的热控系统的结构和控制策略。De Palo等人研究了国际空间站哥伦布舱热力和水力控制回路的稳定性,验证了当前PID算法的稳定边缘和控制器参数变化时系统的稳定性[10]。Valenzano等人应用TeCLA软件以控制算法的增益为参数定义了稳定区域,估计了节点2号舱和节点3号舱液体回路温度控制算法的稳定性,预测了空间站运行周期的危险工况[11]。Solomon等人利用SINDA和TRASYS软件建立了国际空间站美国实验舱-A模块全局数学热模型(TMM),并利用模型预测了实验舱表面温度、冷凝温度、峰值空气温度等参数,估计了输入载荷的整体效应[12]。Zhukov等人运用V-HAB软件模拟了空间站整个飞行任务周期各个状态下温度、湿度等环境参数的动态变化,估计了空间站环境参数的可控性和稳定性[13]。
空间站内部液体主动热控回路的控制是复杂的热力过程,它具有多变量相耦合、大惯性、非线性、难以得到精确数学模型的特点。这些特点使得传统的PID技术难以达到满意的控制效果,其数学模型的不确定又限制了现代控制控制理论的有效应用。模糊控制、自适应控制和神经网络控制等智能控制算法,为解决复杂热工对象的控制提供了新的办法。针对PID控制器对控制对象的参数变化较难适应,而传统模糊控制器存在稳态控制残差的问题,李运泽、董素君等人提出了模糊增量控制算法,它能够很好地运用于航天器电子设备热控问题,如微通道流体冷却网络的协同控制[14]、基于环路热管和百叶窗式辐射器的航天器冷却系统[15]、纳卫星在轨瞬态热辐射环境的地面等效模拟系统[16]。
本文提出了以液冷支路进出口温差和风冷支路冷却量占总冷却量的比值为控制目标的反馈控制策略,采用模糊增量控制算法实现对控制目标精确、快速、稳定的控制。经过在机柜热力学模型上的仿真验证,证明了控制算法和控制策略的有效性和可行性。
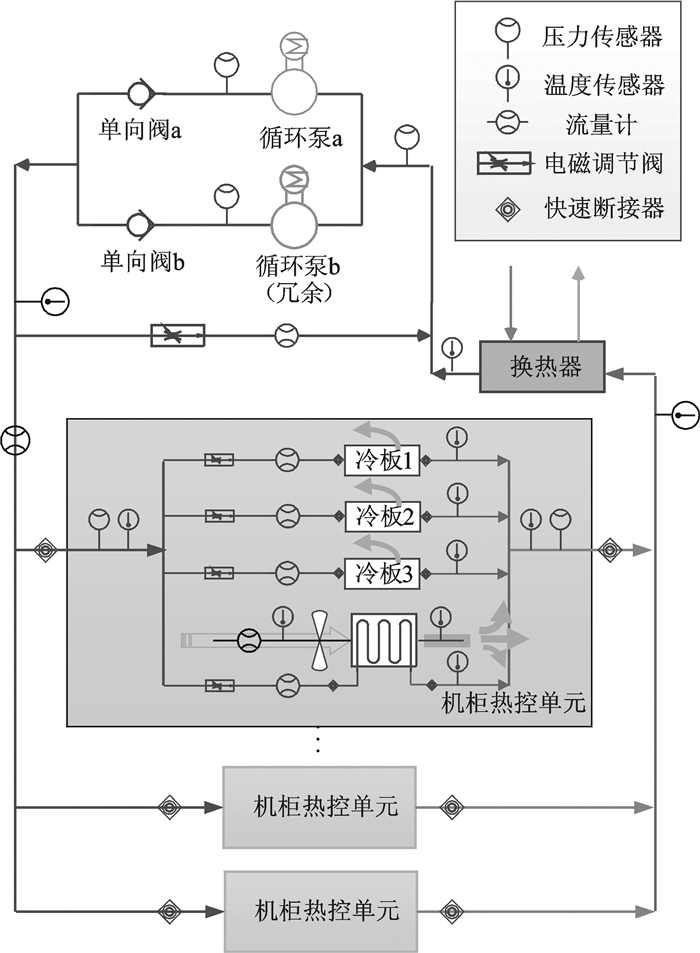
1 模型建立 1.1 系统概述如图 1所示,空间站内部主动热控系统主要由机械泵、阀门、冷板、换热器和单相流体循环回路组成。发热设备安装在冷板上,经冷板导热,将废热通过冷却液体带走。同时,在机柜中内布置风机,带动气体循环完成热量的收集和运输,并通过机柜内置的气-液换热器传递给另一侧的循环液体。冷却液在热总线汇合后进入液-液换热器,将热量传递给外部热控系统的液体后被冷却,最后重新进入机械泵完成循环。冷板在机柜中采用串联或者并联的布置方式,机柜在冷却回路中采用并联的布置方式。为了简便分析和计算,本文将研究对象简化为回路中只有1个机柜,机柜中并联3块冷板的情况。系统的模型可以分为水力模型和热力模型两个部分。
|
图 1 热控系统示意图 Figure 1 Schematic diagram of the thermal control system |
1.2 水力模型
假设循环泵进出口的压差ΔP为定值,流体在管道中的流动遵循下式
| $ {G_{\rm{f}}} = \sqrt {\Delta P/Z} $ | (1) |
式中:Gf为系统总流量,Z为回路总流阻。
各部分流阻的计算如下所示
| $ {Z_{{\rm{w}},i}} = {Z_{{\rm{CP}}}} + {Z_{\rm{M}}} + \frac{{{Z_{\rm{v}}}}}{{\varphi _{{\rm{w}},i}^2}} $ | (2-a) |
| $ {Z_{{\rm{air}}}} = {Z_{{\rm{AH}}}} + {Z_{\rm{M}}} + \frac{{{Z_{\rm{v}}}}}{{\varphi _{\rm{l}}^2}} $ | (2-b) |
| $ \frac{1}{{\sqrt {{Z_{{\rm{rack}}}}} }} = \sum\limits_{i = 1}^3 {\frac{1}{{\sqrt {{Z_{{\rm{w}},i}}} }} + \frac{1}{{\sqrt {{Z_{{\rm{air}}}}} }}} $ | (3) |
| $ Z = {Z_{{\rm{rack}}}} + {Z_{{\rm{HX}}}} + {Z_{\rm{P}}} $ | (4) |
式中:ZCP为冷板的流阻,ZM为流量计的流阻,ZAH为气-液换热器的流阻,Zw, i为液冷支路的总流阻,Zair为气冷支路的总流阻,Zv为阀门的基础流阻,φw, i为液冷支路阀门的开度,i=1~3,φl为气冷支路阀门的开度,ZHX为液-液换热器的流阻,ZP为管道流阻。
各冷却支路的流量分配由下式求出
| $ {G_{{\rm{f}},i}} = \frac{{\sqrt {{Z_{{\rm{rack}}}}} }}{{\sqrt {{Z_{{\rm{w}},i}}} }}{G_{\rm{f}}} $ | (5-a) |
| $ {G_{\rm{l}}} = \frac{{\sqrt {{Z_{{\rm{rack}}}}} }}{{\sqrt {{Z_{{\rm{air}}}}} }}{G_{\rm{f}}} $ | (5-b) |
式中:Gf, i为各液冷支路的流量,Gl为风冷支路的流量。
1.3 热力学模型采用节点热网络法建立机柜的热力学模型,将发热设备、冷板和机柜分别视为集总参数环节,它们的温度和热容分别为(Te, i, Ce, i),(Ts, i, Cs, i),(Tr, Cr),系统的控制方程分别为
| $ \begin{array}{l} {C_{{\rm{e}},i}}\frac{{{\rm{d}}{T_{{\rm{e}},i}}}}{{{\rm{d}}\tau }} = {\mathit{\Phi }_i} - {A_{{\rm{es}},i}}R_{{\rm{es}}}^{ - 1}\left( {{T_{{\rm{e}},i}} - {T_{{\rm{s}},i}}} \right) - \\ \;\;\;\;\;{A_{{\rm{ea}},i}}{h_{{\rm{ea}}}}\left( {{T_{{\rm{e}},i}} - {{T''}_{\rm{a}}}} \right) \end{array} $ | (6) |
| $ \begin{array}{l} {C_{{\rm{s}},i}}\frac{{{\rm{d}}{T_{{\rm{s}},i}}}}{{{\rm{d}}\tau }} = {A_{{\rm{es}},i}}R_{{\rm{es}}}^{ - 1}\left( {{T_{{\rm{e}},i}} - {T_{{\rm{s}},i}}} \right) - \\ \;\;\;\;\;{\eta _i}{G_{{\rm{f}},i}}{c_{\rm{w}}}\left( {{T_{{\rm{s}},i}} - {T_{{\rm{in}}}}} \right) - {A_{{\rm{sr}},i}}R_{{\rm{sr}}}^{ - 1}\left( {{T_{{\rm{s}},i}} - {T_{\rm{r}}}} \right) \end{array} $ | (7) |
| $ \begin{array}{l} {C_{\rm{r}}}\frac{{{\rm{d}}{T_{\rm{r}}}}}{{{\rm{d}}\tau }} = \sum\limits_{i = 1}^3 {{A_{{\rm{sr}},i}}R_{{\rm{sr}}}^{ - 1}\left( {{T_{{\rm{s}},i}} - {T_{\rm{r}}}} \right)} + \\ \;\;\;\;\;\;\;{A_{{\rm{ar}}}}{h_{{\rm{ar}}}}\left( {{T_{\rm{a}}} - {T_{\rm{r}}}} \right) - {A_{{\rm{r0}}}}{h_{{\rm{r0}}}}\left( {{T_{\rm{r}}} - {T_{\rm{0}}}} \right) - \\ \;\;\;\;\;\;\;\gamma {A_{{\rm{r0}}}}{h_{{\rm{r0}}}}\left( {{T_{\rm{r}}} - {T_{\rm{0}}}} \right) \end{array} $ | (8) |
式中:Aes, i为设备和冷板的热传导面积,Aea, i为设备和机柜内空气的热交换面积,Asr, i为冷板和机柜的热传导面积,Aar为机柜内空气和机柜的热交换面积,Ar0为机柜和舱内空气的热交换面积,Res和Rsr为接触热阻,hea, har和hr0为传热系数,ηi为冷板热效率,cw为冷却工质的比热容,Tin为入口冷却工质的温度,T0为舱内空气温度,T″a为气-液换热器出口气体温度,Ta为机柜内空气的平均温度,γ为机柜与周围结构间的热传导量占机柜向舱内空气散热量的比值,计算中假设γ为0.5。
Ta的计算公式为
| $ {T_{\rm{a}}} = \left( {{{T'}_{\rm{a}}} + {{T''}_{\rm{a}}}} \right)/2 $ | (9) |
式中:T′a为气-液换热器的进口空气温度。
冷板热效率的定义为
| $ {\eta _i} = \left( {{T_{{\rm{out}},i}} - {T_{{\rm{in}}}}} \right)/\left( {{T_{{\rm{s}},i}} - {T_{{\rm{in}}}}} \right) $ | (10) |
式中:Tout, i为各液冷支路液体出口温度。
气-液换热器液的热效率ε的定义为
| $ \left\{ {\begin{array}{*{20}{c}} {\varepsilon = \frac{{{T_{{\rm{out}},l}} - {T_{{\rm{in}}}}}}{{{{T'}_{\rm{a}}} - {T_{{\rm{in}}}}}}\;\;\;\;{G_{\rm{w}}}{c_{\rm{w}}} < {G_{\rm{a}}}{c_{\rm{a}}}}\\ {\varepsilon = \frac{{{{T'}_{\rm{a}}} - {{T''}_{\rm{a}}}}}{{{{T'}_{\rm{a}}} - {T_{{\rm{in}}}}}}\;\;\;\;{G_{\rm{a}}}{c_{\rm{a}}} < {G_{\rm{w}}}{c_{\rm{w}}}} \end{array}} \right. $ | (11) |
式中:Ga为空气的质量流量,Tout, l为液侧出口冷却工质的温度。
同时,气-液换热器中气侧和液侧的换热量qAH为
| $ {q_{{\rm{AH}}}} = {G_{\rm{w}}}{c_{\rm{w}}}\left( {{T_{{\rm{out}},{\rm{l}}}} - {T_{{\rm{in}}}}} \right) = {G_{\rm{a}}}{c_{\rm{a}}}\left( {{{T'}_{\rm{a}}} - {{T''}_{\rm{a}}}} \right) $ | (12) |
为方便计算,假设冷板热效率和气-液换热器热效率为定值,联立式(6—12)求解,可得到Te, i, Ts, i, Tr, Tout, i, Tout, l, T′a和T″a。
2 控制器设计载荷机柜热控系统的控制策略是:对于液冷支路,通过传感器测得支路出口液体温度,计算出进出口温度差ΔTi,与设定值进行比较,求出误差和误差变化率,将误差和误差变化率输入模糊增量控制器,经过运算得到阀门开度的增量,作用到执行机构即阀门上,通过调节阀门的大小调节冷却液体的流量,满足控温需求。对于气冷支路,以气冷支路冷却量占总冷却量的比例为被调量,通过调节风扇的功率调节空气通量的大小,使被调量达到设定值。Qa为空气的体积流量,假设空气流量可以在40~220 m3/h范围内连续变化。气冷支路冷却量占总冷却量比例的计算方法为
| $ {\rm{AP = }}\frac{{{q_{{\rm{AH}}}}}}{{{q_{{\rm{AH}}}} + \sum\limits_{i = 1}^3 {{c_{\rm{w}}}{G_{{\rm{f}},i}}\Delta {T_i}} }} $ | (13) |
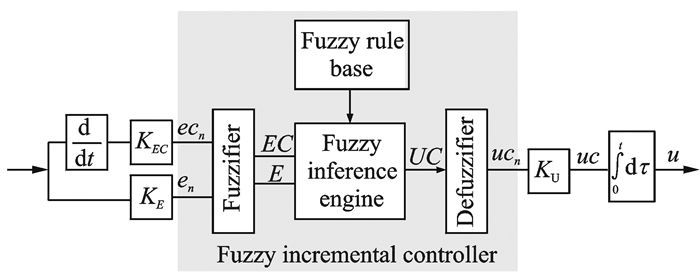
模糊增量控制器主要由模糊化、规则库、模糊推理机构和去模糊化4个部分组成,KE, KEC和KU分别是输入和输出的量化因子,如图 2所示。模糊增量控制器的工作原理详见文献[14-16]。
|
图 2 模糊增量控制器示意图 Figure 2 Implementation of fuzzy incremental controller |
表 1列出了输入和输出空间的模糊集合,及其对应的等级量和语言值。模糊分割的个数决定了该模糊增量控制器的最大可能规则数为7×7=49条。
| 表 1 模糊集合及其语言值 Table 1 Fuzzy set and associated linguistic value |
对于两个输入en,ecn和一个输出变量ucn,均采用高斯型的隶属度函数,即
| $ \mu \left( {x,k} \right) = \exp \left( { - \frac{{{{\left( {x - k \times \frac{1}{3}} \right)}^2}}}{{0.15}}} \right) $ | (14) |
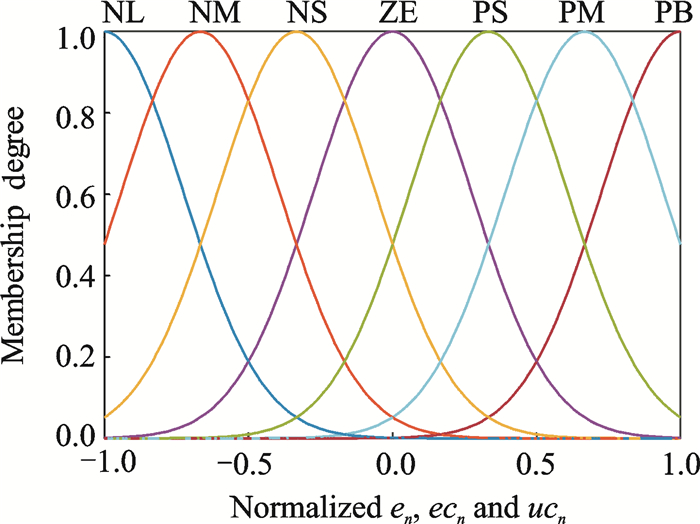
式中:x∈{en, ecn, ucn}, k为某一特定的模糊集合对应的等级量。该控制器采用比较“宽胖”的隶属度函数,故控制效果比较平稳,同时函数之间交叠部分较多,故控制比较灵敏,精度较高。隶属度函数曲线如图 3所示。
|
图 3 隶属度函数曲线 Figure 3 Membership function of the fuzzy sets |
模糊控制规则库由一系列“IF-THEN”型的模糊条件句构成。它的形式为
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{\rm{IF}}}&{{e_n}}&{{\rm{is}}}&{{E_j}}&{{\rm{and}}}&{e{c_n}}&{{\rm{is}}}&{E{C_i},} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{THEN}}}&{u{c_n}}&{{\rm{is}}}&{U{C_{k\left( {i,j} \right)}}} \end{array} \end{array} $ |
其中,Ej和ECi为输入空间的模糊集合,UCk(i, j)为输出空间的模糊集合。液冷支路和风冷支路的模糊规则控制表如表 2, 3所示。
| 表 2 模糊规则控制表(液冷支路) Table 2 Fuzzy control rules (Water-cooled) |
| 表 3 模糊规则控制表(风冷支路) Table 3 Fuzzy control rules (Air-cooled) |
模糊推理采用模糊蕴含最小运算,通过模糊推理得到的是模糊量,需要转变为实际控制的清晰量,采用加权平均的方法求清晰量
| $ u{c_n} = \frac{{\sum\limits_{i = 1}^7 {\sum\limits_{j = 1}^7 {u{c_{R,k\left( {i,j} \right)}}{\mu _{k\left( {i,j} \right)}}} } }}{{\sum\limits_{i = 1}^7 {\sum\limits_{j = 1}^7 {{\mu _{k\left( {i,j} \right)}}} } }} $ | (15) |
式中
| $ {\mu _{k\left( {i,j} \right)}} = {\rm{Min}}\left\{ {\mu \left( {{e_n},i} \right),\mu \left( {e{c_n},j} \right)} \right\} $ | (16) |
式中:ucR, k(i, j)为规则表中第i列,第j行所对应的模糊输出的语言值的等级量的大小。
最终阀门的开度为
| $ {u_{n + 1}} = {u_n} + {K_U} \times u{c_n} $ | (17) |
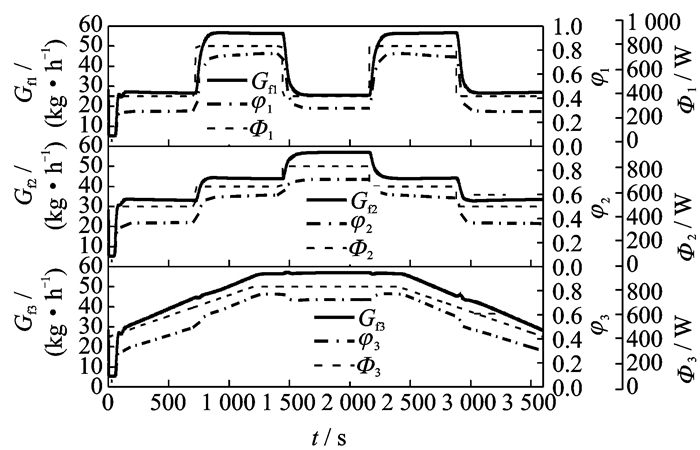
采用Matlab/Simulink软件进行仿真计算。对3块冷板分别施加3种变化规律的热源,模型的计算步长为200 ms,温度和流量的采样周期均为1 s。入口冷却液的温度Tin为20 ℃。液冷支路的控制目标为进出口液体温度差为10 ℃,风冷支路冷却量占总冷却量的控制目标设定值为AP=0.3。液冷支路和风冷支路控制器量化因子的取值如表 4所示。仿真计算的结果如图 4-7所示。
| 表 4 量化因子取值 Table 4 Value of normalized factor |
|
图 4 液冷支路流量响应 Figure 4 Follow rate response of water-cooled branch |
|
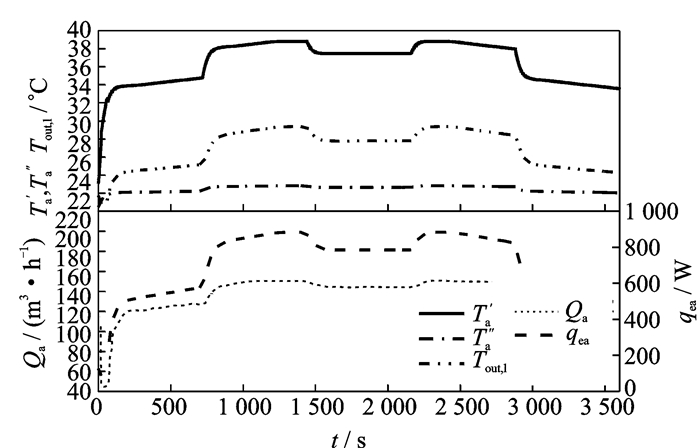
图 5 气冷支路各温度响应 Figure 5 Aircooled branch temperature response |
|
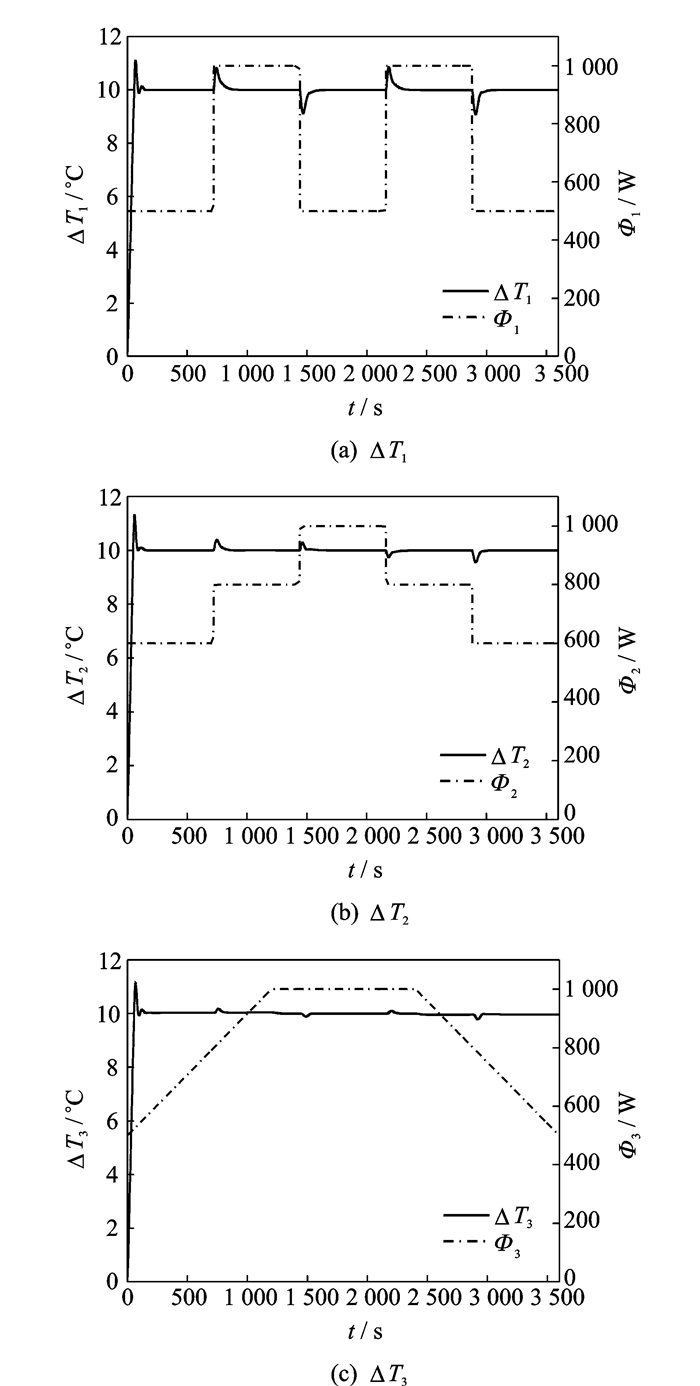
图 6 液冷支路进出口温差响应 Figure 6 Temperature difference response of water-cooled branch |

|
图 7 气冷比例响应 Figure 7 Air-cooling control variable response |
图 4显示了各液冷支路阀门开度和支路流量随时间的变化,可以看到阀门的开度和流量随着热载荷的变化而变化,各支路间的流量扰动较小。当Φ1从500 W上升到1 000 W时,阀门开度从0.3上升到0.7左右,流量从27 m3/h上升到56 m3/h左右。图 5显示了气-液换热器入口温度温度T′a,出口气体温度T″a和出口液体温度Tout, l随时间的变化。从图中可以看出,机柜内空气通量Qa的大小影响了空气和热载荷间热交换量qea的大小,随着qea增大,T′a和Tout, l增大,qea最大为900 W左右,此时空气通量约150 m3/h,而T′a约为39 ℃。在热载荷变化过程中,T″a的变化幅度很小,在22 ℃左右。仿真计算结果符合预期结果,验证了机柜模型的合理性。
图 6和图 7显示了控制系统被调量的响应。从图中可以看出,当支路载荷在0~1 000 W之间变化时,液冷支路进出口的温差能很好地稳定在10 ℃的设定值。机柜总载荷变化时,空气的散热量占液冷和气冷总散热量的比例能够保持在0.3的设定值。控制效果比较精确,响应快速,超调量较小。仿真结果验证了控制策略的有效性和可靠性。
4 结束语针对空间站载荷机柜的热控问题,本文提出了采用模糊增量控制算法,同时以液冷支路进出口温差和风冷冷却量占总冷却量的比例为反馈量,进行热控系统调控的控制策略。为验证控制算法和控制策略的有效性,本文建立了基于单相流体回路,采用液冷结合风冷的热控方式的机柜热控系统模型。仿真结果显示,模型能够很好地反应出热控系统的特性,热控策略能够有效地控制液冷支路的进出口液体温差和风冷支路冷却量比例达到设定值,控制效果精确,超调量较小,响应较快。文章还介绍了模糊增量控制算法的原理,该算法控制效果较好,且具有实现较为简单,运算量小的优点,因此可以广泛应用于航空航天设备的热控制。
| [1] |
HARTUNG R, MOORE K C. A review of space station ECLSS/ITCS automation[R]. SAE Technical Paper, 1995. |
| [2] |
范含林.
载人航天器热管理技术发展综述[J]. 航天器工程, 2007, 16(1): 28–32.
DOI:10.3969/j.issn.1673-8748.2007.01.006 FAN Hanlin. Manned spacecraft thermal management technologies development overview[J]. Spacecraft Engineering, 2007, 16(1): 28–32. DOI:10.3969/j.issn.1673-8748.2007.01.006 |
| [3] |
徐向华, 程雪涛, 梁新刚.
载人航天器主动热控制系统流体回路的优化设计[J]. 宇航学报, 2011, 32(10): 2285–2293.
DOI:10.3873/j.issn.1000-1328.2011.10.030 XU Xianghua, CHENG Xuetao, LIANG Xingang. Design and optimization for fluid loops of active thermal control system in manned spacecraft[J]. Journal of Astronautics, 2011, 32(10): 2285–2293. DOI:10.3873/j.issn.1000-1328.2011.10.030 |
| [4] |
ZHANG Yu, TONG Tiefeng.
Thermal control scheme study of scientific experiment rack of new manned space station[J]. Procedia Engineering, 2016, 157: 374–381.
DOI:10.1016/j.proeng.2016.08.379
|
| [5] |
QUARANTA A, BUFANO G, DE PALO S, et al. Columbus payloads flow rate anomalies[C]//Proceedings of 41st ICES Conference. Portland, Oregon: [s.n.], 2011. |
| [6] |
THURMAN R L. Automation of space station thermal control systems-the important role of software[R]. SAE Technical Paper, 1996. |
| [7] |
PATEL V P, BARIDO R, JOHNSON B. Development of the internal thermal control system(ITCS) for International Space Station (ISS)[R]. SAE Technical Paper, 2001. |
| [8] |
BERTOTTO D, BRAMBATI G, VALENZANO G. ISS node 2 environmental control design[R]. SAE Technical Paper, 2003. |
| [9] |
VALENZANO G, LOMBARDI S, LODDONI G, et al. ISS node 3 TCS analysis and design[R]. SAE Technical Paper, 1999. |
| [10] |
DE PALO S, KLINGBERG T, PERSSON J. Control stability analysis applied to Columbus ATCS[R]. SAE Technical Paper, 2009. |
| [11] |
VALENZANO G, BURZAGLI F, LOMBARDI S. Temperature controller stability resolution for ISS nodes 2& 3 IATCS loops[R].SAE Technical Paper, 2001. |
| [12] |
SOLOMON M E, IBARRA T H. Thermal math model of the Space Station U.S. Laboratory-A model[R].SAE Technical Paper, 1994. |
| [13] |
ZHUKOV A, ROTH C M. Simulation of the temperature and humidity control system of international space station in the virtual habitat[C]//43rd International Conference on Environmental Systems. Vail, Colorado: [s.n.], 2013. |
| [14] |
LI Yunze, LEE K.
Thermohydraulic dynamics and fuzzy coordination control of a microchannel cooling network for space electronics[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 700–708.
DOI:10.1109/TIE.2010.2045999
|
| [15] |
DONG Sujun.
Fuzzy incremental control algorithm of loop heat pipe cooling system for spacecraft applications[J]. Computers & Mathematics with Applications, 2012, 64(5): 877–886.
|
| [16] |
LI Yunze. Intelligent equivalent physical simulator for nanosatellite space radiator[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Singapore: IEEE, 2009. |
 2018, Vol. 50
2018, Vol. 50


