2. 北京航空航天大学航空科学与工程学院, 北京, 100191
2. School of Aeronautic Science and Engineering, Beihang University, Beijing, 100191, China
随着现代飞机对超声速巡航、超机动等方面要求越来越高,飞机逐渐向高压化和大功率化发展,由此带来的系统无效功率的增加和油液温度急剧上升等问题越来越引起了人们的关注[1-3]。研究表明飞机液压系统的压力从21 MPa上升至56 MPa时,液压系统油液温度会从110 ℃上升至180 ℃。液压油温度的升高会带来一系列危害,如油液的粘度下降、氧化分解加速、稳定使用寿命降低等。此外,还会导致液压系统密封件老化,金属腐蚀增加,运动副磨损加剧,工作寿命缩短等相关问题。因此,温度对液压系统的高效工作具有重要的影响。航空柱塞泵作为液压系统中最重要的能量转换装置,是飞机液压系统最主要的热源之一,对飞机液压系统油液温度具有重要的影响。开展柱塞泵的热分析和热设计研究对液压系统温度具有重要的影响。柱塞泵热分析方法的开展对液压系统油温控制在合理水平具有重要的意义[4-6]。
当前柱塞泵的热分析方法主要有:(1)平均油温法和动态油温法,(2)热节点网络法,(3)软件仿真法。同济大学的Li等人[6]使用平均油温方法估算了飞机液压系统在不同飞行阶段的油液温度;中国飞行试验研究院的安玉娇等人[7]对动态油温方法进行了改进。不管是动态油温法还是平均油温法都是比较粗略的研究方法,不能得到比较精确的结果。王宽等人[8]使用了AIMSim等软件对飞机液压系统进行了建模和仿真;空军工程大学的李永林等人[9]利用dymola软件对飞机液压系统中不同的泵源进行了仿真分析,得出了智能泵发热量最小能耗最低的结论。无论基于AIMSim还是dymola的软件仿真法对软件的依赖比较大,不能反映液压系统和元件内部的传热机制。Li等人[10]使用热节点网络法对EHA中柱塞泵进行了热节点建模,并且进行仿真分析。该分析方法不能反映内部的传热机制,且模型中各个参数耦合明显,求解较难。综上所述,当前飞机液压系统热分析方法都不能简洁和准确地求解液压系统及其元件的热变化过程。
基于集中参数热网络模型从机理出发,能够提供一个简单、高效且清晰表征传热过程的热分析方法而受到越来越多研究者的青睐[11-12]。集总参数法指当研究对象内部的导热热阻远小于其表面的对流换热热阻时,可以将整个对象连续分布的质量与热容汇总到一点,系统内部热量的传递可以认为是节点之间通过热阻进行传递,模型中各个节点之间的热阻是关于研究对象的几何尺寸、材料属性和运行参数的相关函数,能够准确表征研究对象的发热机理。
本文采用基于集总参数的热网络模型方法,建立了柱塞泵的热网络模型,在航空柱塞泵工作过程中对其热特性有重要影响的参数进行了甄别,对这些参数变化对柱塞泵热特性的影响进行了仿真,并且详细分析了相关的仿真结果。
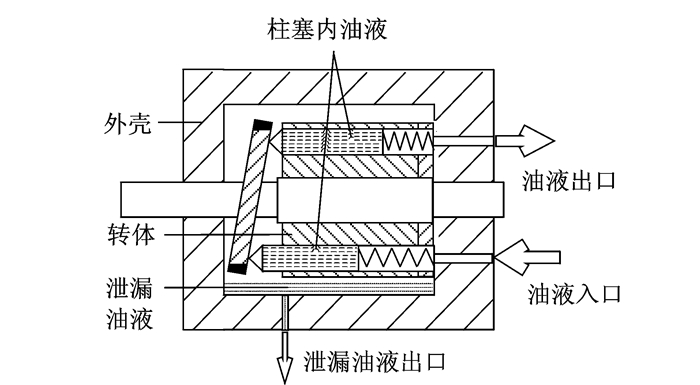
1 航空柱塞泵产热原理航空柱塞泵的示意图如图 1所示。柱塞泵主要有外壳、转体、油液进出口等组成。柱塞泵是一种将机械能转换成液压油压力势能的装置,它的产热原理是:外界的油液不断地输入柱塞泵的柱塞内,通过外界输入功率带动柱塞泵的转轴转动并且对柱塞内的油液做功,柱塞内的油液在转体柱塞的压缩下,从低压油变成高压油。在此过程中,液压油会存在流体动力损失,该损失全部转换成油液的内能,使其温度升高。在柱塞泵转动的过程中,转体内部会存在摩擦损失,该能量损失最终都转换成了转体内部的热能,使转体的温度升高。油液在流入、压缩和和流出的过程中与柱塞泵转体之间存在对流换热,使油液的温度升高。转体内部的高压液压油一部分通过柱塞泵的出口喷出,另一部分会通过转体的缝隙泄漏,最后通过泄漏口流出。这个过程中,泄漏的高压油中的压力势能转换成了油液的内能,使泄漏油液温度升高。从转体泄漏的高压油液会充满柱塞泵的整个壳体,与转体和外壳接触,泄漏油液与转体和外壳之间也存在对流换热。此外,转体和外壳之间紧密连接也存在对流换热。总之,柱塞泵在压缩流体做功的过程中,存在各种能量损失,该能量损失最终都是以热能的形式耗散,最终导致柱塞泵内部各个部件温度上升。
|
图 1 柱塞泵示意图 Figure 1 Schematic diagram of axial piston pump (APP) |
2 柱塞泵热建模 2.1 柱塞泵热阻网络模型
根据集总参数法的热网络模型研究方法,得到柱塞泵的热网络模型示意图如图 2所示。在该图中,将柱塞泵分为4个节点,即流出油液节点、泄漏油液节点、转节点和外壳节点。流出油液节点主要指通过柱塞泵内的柱塞压缩以后从出口流出的油液;泄漏油液节点指将柱塞泵内部从柱塞内泄漏充满柱塞能腔体的油液看成一个节点;转体节点是将柱塞泵内部的转体看成一个节点;外壳节点是将柱塞泵的外壳视为一个节点。此外,由于柱塞泵与外界空气和结构之间存在换热,故还需要加入空气节点和结构节点。图中各个节点之间的换热采用热阻的形式表示。柱塞泵内部4个节点自身热量的变化用热容方式表示。在柱塞泵工作的工程中,认为摩擦损失

|
图 2 柱塞泵热阻网络图 Figure 2 Thermal resistance network of APP |
柱塞泵热网络图的相关表达式如式(1)所示。
| $ {\mathit{\boldsymbol{C}}_{{\rm{pump}}}}\left[ {\begin{array}{*{20}{c}} {{{\dot T}_{{\rm{out}}}}}\\ {{{\dot T}_{{\rm{le}}}}}\\ {{{\dot T}_{\rm{r}}}}\\ {{{\dot T}_{\rm{s}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - R_{{\rm{or}}}^{ - 1}}&0&{R_{{\rm{or}}}^{ - 1}}&0\\ 0&{ - R_{{\rm{sr}}}^{ - 1} - R_{{\rm{lr}}}^{ - 1}}&{R_{{\rm{lr}}}^{ - 1}}&{R_{{\rm{sl}}}^{ - 1}}\\ {R_{{\rm{or}}}^{ - 1}}&{R_{{\rm{rl}}}^{ - 1}}&{ - R_{{\rm{ro}}}^{ - 1} - R_{{\rm{rl}}}^{ - 1} - R_{{\rm{rs}}}^{ - 1}}&{R_{{\rm{rs}}}^{ - 1}}\\ 0&{R_{{\rm{sl}}}^{ - 1}}&{R_{{\rm{rs}}}^{ - 1}}&{ - R_{{\rm{sl}}}^{ - 1} - R_{{\rm{rs}}}^{ - 1} - R_{{\rm{sa}}}^{ - 1}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{T_{{\rm{out}}}}}\\ {{T_{{\rm{le}}}}}\\ {{T_{\rm{r}}}}\\ {{T_{\rm{s}}}} \end{array}} \right] + {{\mathit{\boldsymbol{\dot Q}}}_{{\rm{pump}}}} $ | (1) |
式中:Tout,Tle, Tr和Ts分别为柱塞泵内部流出油液节点的温度、泄漏油液节点的温度、转子的温度和柱塞泵外壳的温度。Ta和Tj分别为外界空气和外界结构的温度。Ṫout, Ṫle, Ṫr和Ṫs分别为流出油液节点、泄漏油液节点、转体节点和外壳节点的温度梯度。Ror, Rrl, Rrs分别为柱塞泵转体与流出油液节点、泄漏油液节点和外壳节点之间的换热热阻,Rsl为外壳与泄漏油液节点之间的换热热阻。Rsa和Rsk分别为柱塞泵外壳节点与外界空气和外界结构之间的换热。Cpump和
| $ {\mathit{\boldsymbol{C}}_{{\rm{pump}}}} = {\rm{Diag}}\left[ {\begin{array}{*{20}{c}} {{c_{\rm{o}}}{m_{{\rm{out}}}}}&{{c_{\rm{o}}}{m_{{\rm{le}}}}}&{{c_{\rm{r}}}{m_{\rm{r}}}}&{{c_{\rm{s}}}{m_{\rm{s}}}} \end{array}} \right] $ | (2) |
| $ {{\mathit{\boldsymbol{\dot Q}}}_{{\rm{pump}}}} = \left[ {\begin{array}{*{20}{c}} {{{\dot Q}_{\rm{h}}} + {G_{{\rm{in}}}}{h_{{\rm{in}}}} - {G_{{\rm{out}}}}{h_{{\rm{out}}}} - {G_{{\rm{le}}}}{h_{{\rm{out}}}}}\\ {{G_{{\rm{le}}}}{h_{{\rm{out}}}} - {G_{{\rm{le}}}}{h_{{\rm{le}}}}}\\ {{{\dot Q}_{\rm{f}}}}\\ {R_{{\rm{sa}}}^{ - 1}{T_{\rm{a}}} + R_{{\rm{sk}}}^{ - 1}{T_{\rm{k}}}} \end{array}} \right] $ | (3) |
式中:co, cr和cs分别为油液、转体和外壳的比热容;mout, mle, mr和ms为流出油液节点、泄漏油液节点、转体节点和外壳节点的质量;
油液经过柱塞泵内部转体的做功从出口排除,流出油液节点与内部转体之间的存在对流换热,其热阻的计算表达式如下
| $ {R_{{\rm{or}}}} = \frac{1}{{{h_{{\rm{or}}}}{A_{{\rm{or}}}}}} $ | (4) |
式中:hor和Aor分别为流出油液与转体之间的对流换热系数和换热面积。
在柱塞泵内部,泄漏油液包裹转体,它们之间存在对流换热,其热阻计算如下
| $ {R_{{\rm{rl}}}} = \frac{1}{{{h_{{\rm{rl}}}}{A_{{\rm{rl}}}}}} $ | (5) |
式中:hrl和Arl分别为泄漏油液与转体之间的对流换热系数和换热面积。
转体与外壳之间为接触热阻,其表达式如下
| $ {R_{{\rm{rs}}}} = \frac{{{\delta _{{\rm{rs}}}}}}{{{h_{{\rm{rs}}}}{A_{{\rm{rs}}}}}} $ | (6) |
式中:δrs, λrs和Ars分别为外壳与转体之间的等效间隙,等效热传导系数和接触换热面积。
泄漏油液与外壳之间为对流换热,其热阻Rsl计算如下
| $ {R_{{\rm{sl}}}} = \frac{1}{{{h_{{\rm{sl}}}}{A_{{\rm{sl}}}}}} $ | (7) |
式中:hsl和Asl分别为泄漏油液与外壳之间的对流换热系数和换热面积。
柱塞泵外壳与结构之间为接触热阻,其表达式如下
| $ {R_{{\rm{sk}}}} = \frac{{{\delta _{{\rm{sk}}}}}}{{{\lambda _{{\rm{sk}}}}{A_{{\rm{sk}}}}}} $ | (8) |
式中:δsk, λsk和Ask分别为外壳与结构之间的等效间隙,等效热传导系数和接触换热面积。
外壳与空气之间为对流换热,其热阻Rsa计算如下
| $ {R_{{\rm{sa}}}} = \frac{1}{{{h_{{\rm{sa}}}}{A_{{\rm{sa}}}}}} $ | (9) |
式中:hsa和Asa分别为泄漏油液与外壳之间的对流换热系数和换热面积。
2.3 功率损失计算柱塞泵工作过程中的摩擦损耗和流体动力损耗表示如下[10]
| $ {{\dot Q}_{\rm{f}}} = \left( {{M_{\rm{u}}} + {M_{\rm{c}}}} \right)\omega $ | (10) |
| $ {{\dot Q}_{\rm{h}}} = \left( {{M_{\rm{n}}} + {M_{\rm{d}}}} \right)\omega $ | (11) |
式中:ω为角转速,单位(rad/s);Mu, Mc, Mn和Md分别为干摩擦力矩、常值摩擦力矩、黏性摩擦力矩和流体动力力矩。各力矩的计算表达式如下
| $ {M_{\rm{u}}} = {k_{\rm{u}}}{p_{{\rm{out}}}}{D_{\rm{m}}} $ | (12) |
| $ {M_{\rm{c}}} = {k_{\rm{c}}}{D_{\rm{m}}} $ | (13) |
| $ {M_{\rm{n}}} = {k_{\rm{n}}}\mu {D_{\rm{m}}}n $ | (14) |
| $ {M_{\rm{d}}} = {k_{\rm{d}}}\rho {\alpha ^3}{n^2}D_{\rm{m}}^{\frac{5}{3}} $ | (15) |
| $ \alpha = \frac{{2{\rm{ \mathsf{ π} }}{G_{{\rm{out}}}}}}{{{D_{\rm{m}}}\omega \rho }} $ | (16) |
式中:ku, kc, kn和kd分别为干摩擦力矩、常值摩擦力矩、粘性摩擦力矩和流体动力力矩的系数;pout为油液出口压力;Dm为柱塞泵排量;ρ和μ为油液的密度和粘度;α和n分别为柱塞泵的斜盘倾角和转速。
2.4 流体状态计算流入柱塞泵的油液在转体的作用下,从低压变为高压油液,其中一部分从出口流出,另一部分通过转体活塞缝隙泄漏,通过泄漏控流出。油液之间的关系可以表示如下
| $ {G_{{\rm{in}}}} = {G_{{\rm{out}}}} + {G_{{\rm{le}}}} $ | (17) |
关于柱塞泵内部油液泄漏油液的质量流量的表达式如下
| $ {G_{{\rm{le}}}} = {C_1}{D_{\rm{m}}}\rho {p_{{\rm{out}}}}/\mu $ | (18) |
式中:C1为泄漏系数。
| $ {p_{{\rm{out}}}} = {p_{{\rm{in}}}} + \Delta p $ | (19) |
柱塞泵输出功率与输出油液之间的关系表示如下
| $ {G_{{\rm{out}}}} = \frac{{{W_{{\rm{out}}}}}}{{\Delta p}} $ | (20) |
式中Wout为柱塞泵输出功率。
柱塞泵的输入功率转换成两个部分:一部分将流入柱塞泵内部油液的压力势能;另一部分转换成柱塞泵的内部的损耗,包括摩擦损耗和流体动力损耗。其能量平衡方程如下
| $ {M_{{\rm{in}}}}{\omega _{{\rm{in}}}} = {G_{{\rm{in}}}}\left( {{p_{{\rm{out}}}} - {p_{{\rm{in}}}}} \right) + {{\dot Q}_{\rm{f}}} + {{\dot Q}_{\rm{h}}} $ | (21) |
式中Min为输入转矩。
柱塞泵的效率计算如下
| $ \eta = \frac{{{G_{{\rm{out}}}}\left( {{p_{{\rm{out}}}} - {p_{{\rm{in}}}}} \right)}}{{{G_{{\rm{in}}}}\left( {{p_{{\rm{out}}}} - {p_{{\rm{in}}}}} \right) + {{\dot Q}_{\rm{f}}} + {{\dot Q}_{\rm{h}}}}} $ | (22) |
在仿真过程中,柱塞泵的仿真参数设计如表 1所示。在飞机飞行过程中,柱塞泵的转速、转矩和外界的对流换热系数会随着飞行工况而改变。转速和转矩主要对柱塞泵内部的功率损耗有重要影响,即对产热有重要影响。对流换热系数对柱塞泵的散热有重要影响。因此,转速、转矩和对流换热系数对柱塞泵的热特性有重要的影响。本文设置了4种工况分别进行了仿真,具体如表 2所示。在仿真过程中,设置输入油液温度恒定为55 ℃。
| 表 1 仿真参数 Table 1 Simulation parameters |
| 表 2 仿真工况设置 Table 2 Simulation case |
工况1为柱塞泵在转速4 411 r/min、转矩为80 N·m和对流换热系数为20 W/(m2·K)启动,其仿真结果如图 3所示。在初始时刻,柱塞泵内部各节点的温度都为25 ℃,当柱塞泵开始工作以后,55 ℃的油液进入柱塞泵,柱塞泵内部的温度开始急剧上升,经过大约250 s的调整时间,各个节点的温度达到稳态。此时柱塞泵内的转子温度最高,为90.1 ℃,然后依次为外壳节点温度、泄漏节点温度和出口油液节点温度,分别为88.6,79.1和58.7 ℃。转体节点的温度高是因为所有的摩擦损失都集中在转体节点造成了温升。柱塞泵外壳和转体之间紧密接触,热阻很小,从转体传递给柱塞泵的热量较多,导致外壳的温升也很大。流体的动力损失全部集中在流出节点,由于油液的比热容比较大,流出节点油液的温升只有3.7 ℃。泄漏油液的温度比流出节点的温度要高,是因为从流出节点泄漏的油液内部的压力势能转换成了内能,造成温升。

|
图 3 柱塞泵在工况1下启动各节点的温度 Figure 3 Temperature of nodes in APP under Case 1 |
工况2在柱塞泵达到热稳态以后,为保持转速和对流换热不变,在500 s时,转矩从80 N·m增加到120 N·m后柱塞泵的热特性变化,其相关的仿真结果如图 4所示。从图中可以得出,在500 s以后,柱塞泵各个节点的温度逐渐降低,经过约100 s重新达到稳态。各个节点的温度下降为1~3 ℃, 柱塞泵的效率从74.4%上升为82.6%。转矩的增加导致了柱塞泵效率的提升,说明柱塞泵输出油液中,输出单位质量油液所引起的柱塞泵损耗减小,单位质量流量的油液可吸收的热量降低,导致油液温度降低,通过柱塞泵内部的热阻网络传热,最终导致柱塞泵内部所有的温度降低。

|
图 4 柱塞泵转矩增加时各个节点的温度变化 Figure 4 Temperature of nodes in APP when torque increasing |
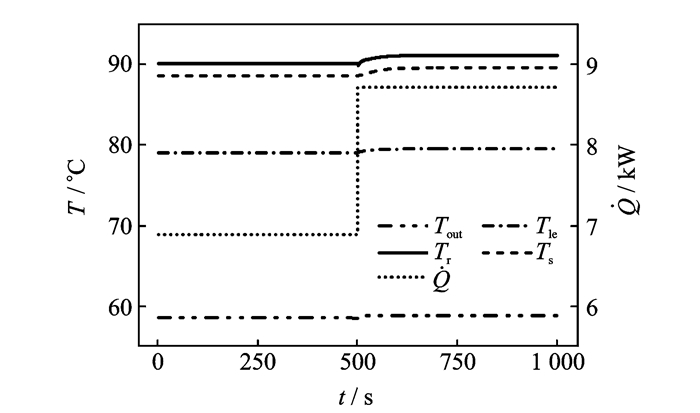
工况三为保持转矩和对流换热系数不变,在500 s时,转速从4 411 r/min增加20%到5 292 r/min后柱塞泵的热特性变化,其相关的仿真结果如图 5所示。从图中可以发现,在500 s以后,柱塞泵各个节点的温度逐渐升高,经过约100 s重新达到稳态。泄露节点和流出节点的温升比较小,约为1 ℃,外壳节点和转体节点温升比较明显,约为3 ℃。此外,柱塞泵的总损耗(包括摩擦损耗
|
图 5 转速提高20%后柱塞泵内各个节点温度变化 Figure 5 Temperature of nodes in APP when speed increasing |
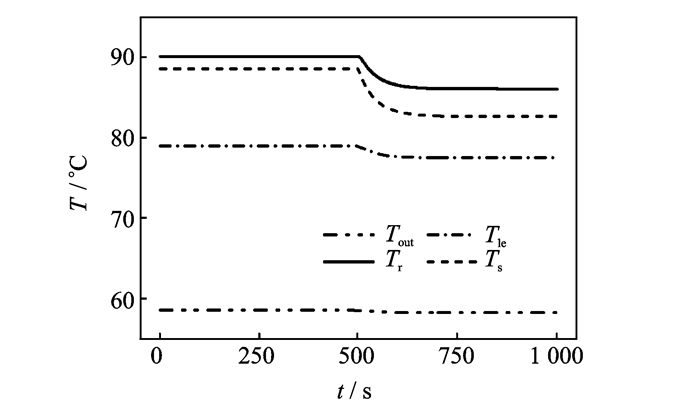
工况4为保持转速和转矩不变,对流换热系数在500 s时从20变为80,其相关的仿真结果如图 6所示。从图中可以得出,在对流换热系数增加以后,柱塞泵各节点的温度逐渐降低,经过约200 s重新达到稳态。外壳温度下降幅度最大,为5.9 ℃,其次分别是转体、泄漏节点和流出节点,分别为4.0,1.5和0.3 ℃。说明随着对流换热系数增加,柱塞泵与外界的换热加快导致了外壳温度的大幅度下降,转体由于与外壳之间的热阻很小导致转体的温度下降也比较大。
|
图 6 外界对流换热系数增加时柱塞泵内部各个节点的温度变化 Figure 6 Temperature of nodes in APP when ambient convection coefficient increasing |
4 结束语
本文针对飞机液压系统中柱塞泵热分析的问题,采用基于集总参数的热网络模型方法,建立了柱塞泵的热网络模型,通过设置不同转速、转矩和对流换热系数的4种工况,仿真分析了转速、转矩和对流换热系数变化时柱塞泵瞬态热特性。仿真结果显示,转速增加以后,损耗会上升导致温度上升;转矩上升会导致柱塞泵效率提升,油液的温度降低;外界对流换热系数增加会加速柱塞泵与外界的换热,导致柱塞泵温度的降低。
| [1] |
WANG J X, LI Y Z, YU X K, et al.
Investigation of heat transfer mechanism of low environmental pressure large-space spray cooling for near-space flight systems[J]. International Journal of Heat and Mass Transfer, 2018, 119: 496–507.
DOI:10.1016/j.ijheatmasstransfer.2017.11.128
|
| [2] |
OUYANG X P, GAO F, YANG H Y.
Model analysis of the aircraft hydraulic system pipeline[J]. Journal of Aircraft, 2012, 49(4): 1168–1174.
DOI:10.2514/1.C031660
|
| [3] |
BERGADA J M, KUMAR S, DAVIES D, et al.
A complete analysis of axial piston pump leakage and output flow ripples[J]. Applied Mathematical Modelling, 2012, 36(4): 1731–1751.
DOI:10.1016/j.apm.2011.09.016
|
| [4] |
ANCIK Z, VLACH R.
Thermal phenomena modeling of aircraft electronic unit[J]. Engineering Mechanics, 2011, 18(5/6): 281–288.
|
| [5] |
JOHANSSON B, ANDERSSON J, KRUS P.
Thermal modelling of an electro-hydrostatic actuation system[J]. Recent Advances in Aerospace Actuation Systems and Components, 2001, 5(2): 13–15.
|
| [6] |
LI J, XU L J, ZHANG X, et al. An estimation method of the fluid temperature foe commercial aircraft hydraulic system[C]//International Conference of Machine Automotive control Engineer. Wuhan, China: [s.n.], 2010. |
| [7] |
安玉娇, 江辉军, 秦成.
飞机液压系统动态油温计算方法优化[J]. 航空科学技术, 2015, 26(2): 54–58.
DOI:10.3969/j.issn.1007-5453.2015.02.012 AN Yujiao, WU Huijun, QIN Cheng. The optimization of dynamic temperature calculation method for aircraft hydraulic system[J]. Aeronautical Science & Technology, 2015, 26(2): 54–58. DOI:10.3969/j.issn.1007-5453.2015.02.012 |
| [8] |
王宽, 黄喜平, 王鸿鑫.
基于AMESim的大型飞机液压能源系统热特性仿真分析方法[J]. 流体传动与控制, 2006, 76(3): 23–27.
WANG Kuan, HUANG Xiping, WANG Hongxin. Thermal-hydraulic system modeling and simulation of large aircraft hydraulic systems based on AMESim[J]. Fluid Power Transmission & Control, 2006, 76(3): 23–27. |
| [9] |
李永林, 徐浩军, 曹克强, 等.
航空柱塞泵全工况效率分析及热力学建模[J]. 北京航空航天大学学报, 2010, 36(12): 1469–1472.
LI Yonglin, XU Haojun, CAO Keqiang, et al. Efficiency analysis and thermal hydraulic modeling of aerial piston pump at whole work condition[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(12): 1469–1472. |
| [10] |
LI C G, JIAO Z X.
Thermal-hydraulic modeling and simulation of piston pump[J]. Chinese Journal of Aeronautics, 2006, 19(4): 354–358.
DOI:10.1016/S1000-9361(11)60340-3
|
| [11] |
JADRIC I, BOROJEVIC D, JADRIC M.
Modeling and control of a synchronous generator with an active DC load[J]. IEEE Transactions on Power Electronic, 2000, 15(2): 303–311.
DOI:10.1109/63.838103
|
| [12] |
MA W M, HU A, LIU D Z, et al.
Stability of a synchronous generator with diode-bridge rectifier and back-EMF load[J]. IEEE Transactions on Energy Conversion, 2000, 15(4): 458–463.
DOI:10.1109/60.900508
|
 2018, Vol. 50
2018, Vol. 50


