2. 日照公路建设有限公司, 日照, 276826
2. Rizhao Highway Construction Co. Ltd., Rizhao, 276826, China
水泥稳定碎石基层结构在早龄期已出现开裂现象,基层的开裂直接影响沥青面层的路用性能,因此,对水泥稳定碎石基层结构早龄期变形进行监测与分析是非常必要的。由于基层内温度和水分的变化,早龄期的水泥稳定碎石基层内部会产生温度场和湿度场,从而产生收缩应变,包括干缩应变和温缩应变。
目前,对半刚性基层收缩应变的监测方法有室内试验、现场试验和数值模拟3类方法。现场试验主要是通过埋入振弦式应变传感器来测量半刚性基层的收缩应变,如:王国杰等[1]采用振弦式应变计监测混凝土结构早龄期的应力相关应变,测试结果表明:使用振弦式应变计可以是混凝土结构应力相关应变计算更加简便、精确,还有助于揭示混凝土早龄期水化、变形等方面的相互关系和应力相关应变的形成机理。吕惠卿等[2]将振弦应变计埋入混凝土梁试件和真实混凝土路面,进行了相关的室内和室外力学试验,以验证振弦式应变计在混凝土路面的力学性能测试应用中的可行性,为其在野外真实水泥混凝土路面使用性能的长期检测应用提供了理论依据和实践经验。吴跃红等[3]在混凝土试件中埋入振弦式应变计测试混凝土的线膨胀系数,得到了混凝土线膨胀系数随龄期变化的规律,即混凝土线膨胀系数在早龄期(2~3 d)变化较为剧烈,后期趋向均匀,并略有减小。室内试验如张鹏等[4]通过室内试验研究聚丙烯纤维水泥稳定碎石的收缩性能,试验结果表明:在一定的纤维掺量范围内,聚丙烯纤维水泥稳定碎石具有良好的抗收缩性能,应用于路面基层可提高路面的抗裂性能。数值模拟一般是借助大型通用软件ABAQUS等,如王艳等[5-6]借助ABAQUS建模分析不同水泥剂量的水泥稳定碎石基层结构内和不同开裂状态的水泥稳定碎石基层沥青路面因失水或降温引起的收缩应力,结果表明:水泥剂量增加会增大基层内的收缩应力;对于新铺筑的基层,因失水引起的收缩应力较温差的影响更为显著。
目前对半刚性材料的干缩和温缩进行了大量的研究,并取得了一定的成果,但对早龄期水泥稳定碎石的研究成果有限。鉴于以上研究方法的可行性,本文利用ABAQUS有限元软件对半刚性基层结构进行建模,并结合现场测量的数据,对水泥稳定碎石基层的早期收缩应变进行分析。结合现场试验路段实际测量的温度,对三维模型施加温度荷载,得出并分析基层结构的早期温度场以及收缩应变的变化规律,为半刚性基层沥青路面结构的基层设计提供一些参考意见。
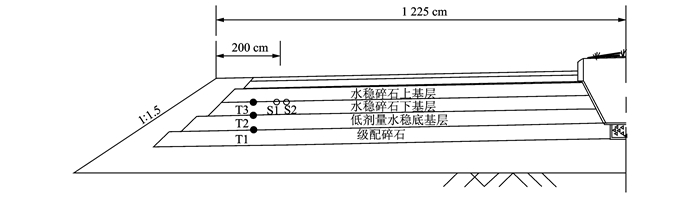
1 有限元模型 1.1 基层有限元模型的建立本文有限元模型的建立基于山东省一条试验路段的路面结构。试验路段的路面结构为18cm级配碎石+18cm底基层+18cm下基层+18cm上基层+透层、封层+6 cm AC-20C+粘层+4 cm AC-13C,基层为底基层、下基层、上基层3层连铺,施工中无时间间隔,见图 1。试验路段铺设于2014年10月19日。为详细记录养生阶段基层温度、应变的变化,在路面结构中埋设了温度、应变传感器,T1,T2,T3是水稳碎石基层、底基层中的温度传感器所埋设的位置,每层埋设2个温度传感器,3层共埋设6个温度传感器;S1,S2是水稳碎石基层的振弦式应变传感器。
|
图 1 应变传感器布置图 Figure 1 Arrangement of strain sensor |
利用ABAQUS软件,按照上述实际路面结构建立三维有限元模型,模型的大小为5m×5 m×10m。由于水泥稳定碎石基层铺设完成后一个月才开始面层的铺设,为了与实际情况一致,模型中未加入面层(见图 2)。其中,z方向为行车方向,y方向为结构深度方向,x方向为横向。为了简化问题的分析计算,假设路面各结构层连续且各向同性;层与层之间不考虑热阻问题。

|
图 2 三维有限元模型 Figure 2 Three-dimensional finite element model |
1.2 温度场分析参数的确定
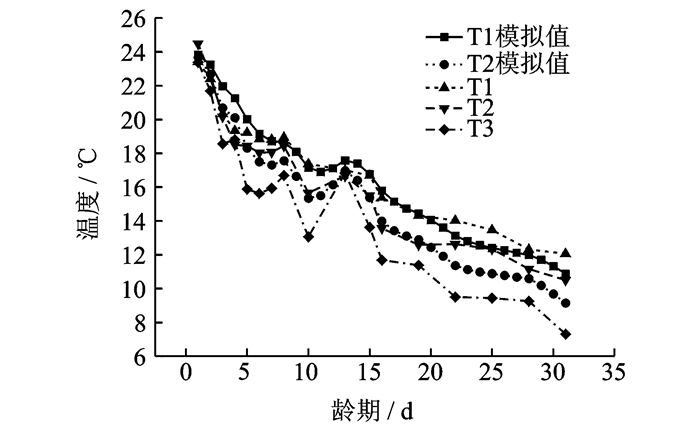
在路面结构材料参数的取值上参考李辉[7]和蒋默识[8]的研究数据,确定了几种热分析参数,即热传导率、比热容以及密度,材料热分析参数见表 1。前人在研究温度场时还会考虑外部温度、气候条件、路面与空气的热交换以及太阳辐射,通过编辑子程序进行模拟分析,本文旨在研究基层早期一段时间内的收缩应变,需要不同龄期的数据,为了保证模拟更加接近实际环境,上基层底面的温度数据采用试验路段已经测得的T3处温度数据,即给定温度边界条件。试验路段温度传感器T1,T2,T3测得的不同龄期的温度数据见图 3,其中图中温度传感器T1,T2,T3的数据为平均值,其最大标准差分别为0.094,0.125和0.110 ℃,可见实测的温度数据较为准确。
| 表 1 半刚性基层的温度场参数 Table 1 Temperature field parameters of semi-rigid base |
|
图 3 基层内各深度处温度的实测值与模拟值 Figure 3 Measured and simulated values of temperature at various depths in the base |
1.3 收缩应变分析参数的确定
半刚性基层收缩应变的分析基于其湿度场和温度场的耦合分析,主要需要弹性模量、泊松比、温缩系数以及干缩系数4个参数。半刚性基层材料不同龄期的回弹模量不同,根据顾吟等[9]的研究,采用拟合方程,见式(1),确定基层材料的弹性模量。拟定的参数见表 2,3。
| $ E = 493.57d - 240.57 $ | (1) |
| 表 2 收缩应变参数 Table 2 Shrinkage strain parameters |
| 表 3 基层模量取值 Table 3 Modulus values of base course |
式中:E为回弹模量;d为龄期。
根据相关研究,水泥稳定碎石材料在早期一个月内的总失水率约为3.5%,根据应变相等原则将干缩转化为相应的降温幅度施加在模型上。
2 结果分析 2.1 不同龄期温度场的分布由于水泥稳定碎石基层早期的干缩变形主要由材料失水引起,无外在荷载施加,所以干缩变形的产生一般是通过降低温度来模拟。温度模拟是否准确直接影响到水泥稳定碎石早期收缩应变发展规律的分析。为验证温度模拟的准确性,以上基层底面的温度T3为温度边界条件,模拟计算了下基层底面温度T2和底基层底面温度T1。实测温度值T1,T2与有限元模拟值见图 3。经过T1,T2模拟值与T1,T2实测值对比可知,实际测量和数值模拟的计算结果误差在5%以内,由此验证了数值模拟温度场分析的可靠性。
由于试验路段位于山东,铺设于2014年10月19日,此时正处于北方的秋季,天气越来越冷,环境温度逐渐降低。由图 3可见,无论是T1,T2还是T3,其温度均随着时间的增加逐渐降低。到2014年11月18日(龄期31 d)时,T1下降了1 1.4 ℃,T2下降了14 ℃,T3下降了16.4 ℃。这表明路面温度的变化趋势和环境温度变化趋势相同,随气温变冷,路面温度降低。另外还可以看出,由于路面深度不同,路面温度降低的程度不同。T1位于底基层底面,温度降低了11.4 ℃;T2位于下基层底面,温度降低了14 ℃;T3位于上基层底面,温度降低了16.4 ℃。这表明,当环境温度降低时,路面内部越浅,其温度降低越大,路面内部越深,其温度降低越小。即随着基层深度增加,温度逐渐升高,T1位置比T2位置深,T1的温度比T2的温度高,下基层的温度要高于上基层的温度。造成这种现象的原因主要是随深度增加,路面材料的热量损失越来越小,热传递过程长,热传递较慢。
另外,由图 3还可以看出,基层表面温度的变化,影响其内部温度的变化。当基层表面降温时,基层内部的温度也会随之降低。从第1天至第3天,温度持续降低,层间的温度差也逐渐加大;第10天至第13天,基层层顶的温度升高,基层层间的温度差逐渐减小。即基层层顶的温度降低时的层间温度差比基层层顶的温度升高时的层间温度差要大。这说明,温度的降低比温度的升高对半刚性基层内温差变化的影响大。
2.2 基层厚度对温度场的影响基层内温度分布梯度的增大,会使基层所产生的拉应力逐渐增大,从而影响沥青面层的路用性能,因此需对不同基层厚度内的温度场进行分析研究。
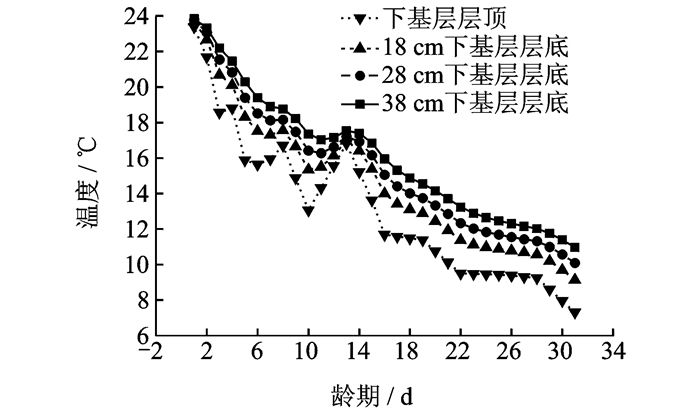
本文给定3种不同的下基层厚度,分别为18,28和38 cm,其他结构保持不变。计算所得的温度场结果见图 4。
|
图 4 不同基层厚度的基层温度分布 Figure 4 Temperature distribution of base with different base thickness |
由图 4可知,基层厚度的变化对基层的温度场影响较大。随着基层厚度的增加,基层层顶与基层层底间的温度差逐渐增大。基层受温度场影响的一个月内,下基层厚度为18 cm时,层间平均温差为1.55 ℃;下基层厚度为28 cm时,层间平均温差为2.35 ℃;下基层厚度为38 cm时,层间平均温差为3.10 ℃。这意味着,基层厚度每增加1 cm,基层层顶与层底的温度差平均增加4.5%。
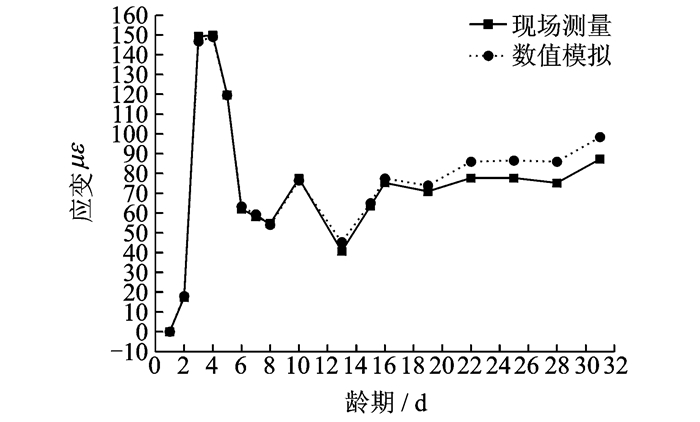
2.3 不同龄期收缩应变的变化试验路段铺设于2014年10月19日,监测时间从2014年10月20日至2014年11月18日,总共一个月的时间,监测水泥稳定碎石基层早龄期的收缩应变发展规律。现场应变传感器测量结果以及数值模拟分析结果见图 5,其中试验路段测得的收缩应变为两个振弦式传感器的平均值,其最大标准差为1.873με,可见实测数值较为准确。
|
图 5 现场测量与数值模拟所得的基层早龄期的收缩应变 Figure 5 Shrinkage strain of base measured by field and numerical modeling in early age |
由图 5可知,现场实测和数值模拟的结果基本保持一致,两者之间的平均误差在5%以内,故数值模拟分析结果较为准确。
水泥稳定碎石基层的收缩应变在水泥稳定碎石基层铺设完成后的一个月内不断变化。基层铺设完成的第1天测得的收缩应变作为基准点,视为0应变;第3天至第4天,由于基层内失水量的增加和温度的降低,基层的收缩应变迅速增大;其后,基层内的失水量减少,干缩对基层收缩应变的影响逐渐减小,基层内的收缩应变基本随温度的变化而变化。
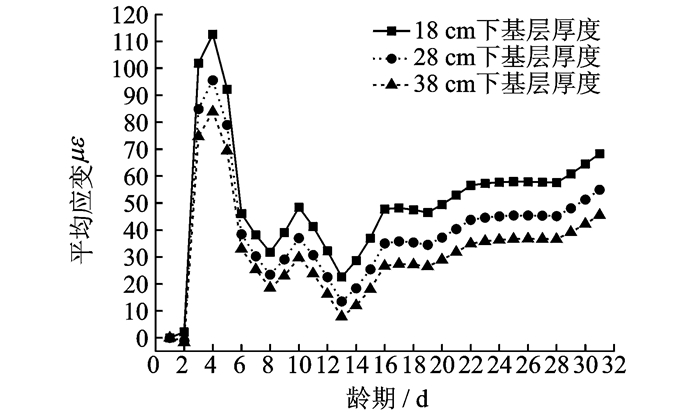
2.4 基层厚度对收缩应变分布的影响基层厚度延用2.2节中的下基层的厚度,即18,28和38 cm,分析其对收缩应变的影响。数值模拟结果见图 6。
|
图 6 不同基层厚度的基层平均收缩应变分布图 Figure 6 Average shrinkage strain distribution of base with different base thickness |
由图 6可知,不同的基层厚度对基层本身的收缩应变有一定的影响。基层厚度的增加,使得基层内平均收缩应变逐渐减小。当基层的厚度从18 cm增加到28 cm时,基层的厚度每增加1 cm,其平均收缩应变减小2.23%;当基层厚度从28 cm增加到38 cm时,基层厚度每增加1 cm,其平均收缩应变减小1.91%。
3 结论(1) 基层的收缩应变在基层铺设结束的前7天受干缩影响较大,其后与温度呈负相关,即基层内温度降低,其收缩应变增大,反之亦然。
(2) 温度的降低比温度的升高对水泥稳定碎石基层内温差变化的影响大。当基层层顶温度升高时,基层层顶与层底的温度差逐渐减小;当基层层顶的温度降低时,基层层顶与层底的温度差逐渐增大。
(3) 基层层顶和基层层底的温度差随着基层厚度的增加而逐渐增大。当基层的厚度在18~38 cm时,基层厚度每增加1 cm,基层层顶与层底的温度差增加4.5%。
(4) 基层厚度的增加,基层内平均收缩应变减小,但是随着基层厚度的增大,基层收缩应变随深度的变化幅度逐渐减小。当基层的厚度从18 cm增加到28 cm时,基层的厚度每增加1 cm,其产生的平均收缩应变减小2.23%;当基层厚度从28 cm增加到38 cm时,基层厚度每增加1 cm,其产生的平均收缩应变减小1.91%。
| [1] |
王国杰, 郑建岚.
混凝土结构早龄期应力相关应变现场监测与分析[J]. 工程力学, 2009, 26(6): 61–73.
WANG Guojie, ZHENG Jianlan. In situ monitoring and analysis for stress-dependent strains of early age concrete structures[J]. Engineering Mechanics, 2009, 26(6): 61–73. |
| [2] |
吕惠卿, 张湘伟, 张荣辉, 等.
振弦式应变计在水泥混凝土路面力学性能测试中的应用[J]. 公路交通科技, 2007(2): 61–63.
DOI:10.3969/j.issn.1002-0268.2007.02.016 LV Huiqing, ZHANG Xiangwei, ZHANG Ronghui, et al. Application of vibrating wire strain gauge in the test of mechanical properties of cement concrete pavement[J]. Journal of Highway and Transportation Research and Development, 2007(2): 61–63. DOI:10.3969/j.issn.1002-0268.2007.02.016 |
| [3] |
吴跃红, 曾世东.
振弦式应变计测试混凝土膨胀系数的研究[J]. 交通标准化, 2014, 42(23): 78–81.
WU Yuehong, ZENG Shidong. Linear expansion coefficient of concrete tested by vibrational chord strain gauge[J]. Transportation Standardization, 2014, 42(23): 78–81. |
| [4] |
张鹏, 李清富, 黄承逵.
聚丙烯纤维水泥稳定碎石收缩性能[J]. 交通运输工程学报, 2008, 8(4): 30–34.
DOI:10.3321/j.issn:1671-1637.2008.04.007 ZHANG Peng, LI Qingfu, HUANG Chengkui. Shrinkage properties of cement stabilized macadam reinforced with polypropylene fiber[J]. Journal of Traffic and Transportation Engineering, 2008, 8(4): 30–34. DOI:10.3321/j.issn:1671-1637.2008.04.007 |
| [5] |
王艳, 倪富强, 李强, 等.
水泥稳定碎石基层横向收缩裂缝控制研究[J]. 公路交通科技, 2008, 25(2): 45–49.
DOI:10.3969/j.issn.1002-0268.2008.02.010 WANG Yan, NI Fujian, LI Qiang, et al. Study on controlling of transverse shrinkage cracking in cement stabilized macadam base[J]. Journal of Highway and Transportation Research and Development, 2008, 25(2): 45–49. DOI:10.3969/j.issn.1002-0268.2008.02.010 |
| [6] |
王艳, 倪富强, 马翔.
不同基层开裂状态的沥青路面应力对比[J]. 交通运输工程学报, 2008, 8(6): 34–39.
DOI:10.3321/j.issn:1671-1637.2008.06.007 WANG Yan, NI Fujian, MA Xiang. Stress comparison of asphalt pavements with different base crack states[J]. Journal of Traffic and Transportation Engineering, 2008, 8(6): 34–39. DOI:10.3321/j.issn:1671-1637.2008.06.007 |
| [7] |
李辉.沥青路面车辙形成规律与温度场关系研究[D].南京: 东南大学, 2007.
LI Hui. Research on the relationship between rutting and temperature field of asphalt pavements[D]. Nanjing: Southeast University, 2007. |
| [8] |
蒋默识.水泥稳定碎石基层热物性参数研究[D].西安: 长安大学, 2012.
JIANG Moshi. Research on thermal physical parameters of cement stabilized macadam base[D]. Xi'an: Chang'an University, 2012. |
| [9] |
顾吟, 方辉, 王金昌.
水泥稳定碎石基层早期力学监测及数值模拟分析[J]. 公路交通科技, 2013, 30(8): 51–53.
GU Yin, FANG Hui, WANG Jinchang. Early mechanical monitoring and numerical simulation analysis of cement stabilized crushed stone base[J]. Journal of Highway and Transportation Research and Development, 2013, 30(8): 51–53. |
 2018, Vol. 50
2018, Vol. 50


