有限的停机位资源已经成为制约大型机场发展的瓶颈。针对现阶段机场拥堵严重的状况,对停机位进行合理的指派,有利于提高机场、航空公司和旅客三方的满意度,对解决目前机场场面拥堵问题具有重要意义。
关于停机位指派的研究,Lim等[1]首次建立以最小化步行距离为目标函数的停机位指派动态模型,采用启发式算法对模型进行求解。此后,Seker等[2]建立了基于航班起降时间的不确定性的停机位指派鲁棒性优化模型。熊杰等[3]为了提高机场容量,针对多跑道机场,建立以最小化航空器滑行距离为目标的停机位指派模型。Diepen[4]、Maharjan[5]、Jiang[6]等分别进行实地调研、以最小化航空器滑行燃油成本、最小化总步行距离为主要目标,考量实地可操作性、公平性和旅客步行距离等因素。Dorndorf等[7]在最小化未分配停机位的航空器数量的基础上以最大化鲁棒性为目标建立停机位多目标指派模型并进行求解。Niku lin等[8]建立了以最小化牵引活动数量,最小化新的停机位指派计划和参考计划的绝对偏差为目标的多目标停机位指派模型。Prem等[9]建立了成本考量下的最大化停机位指派计划鲁棒性的多目标停机位指派模型。杨文东等[10]以航班延误和停机位空闲时间总和最小为目标,构建停机位指派模型。王笑天等[11]建立增大停机位鲁棒性指派模型并采用列生成算法进行求解。解英全[12]将乘客步行总距离最短和航空器总耗油最少设置为停机位指派阶段的目标,实现停机位分配模型的构建。对于停机位指派的模型仿真求解,文献[13]提出采用启发式方法和随机方法结合的方法自上而下求解。Wang等[14]采用了蚁群算法对延误航班的实时再指派进行仿真验证,证明了其优越性。Liu等[15]应用混合集合规划(Mixed set programming, MSP)和序贯博弈的方法对模型进行求解,大大节约了计算时间。
纵观国内外停机位指派研究,国内外学者主要以旅客步行距离、预指派方案的鲁棒性和航空器滑行燃油成本作为优化目标建立单目标模型,或是兼顾停机位空闲时间或航空公司公平性建立多目标停机位指派优化模型。但是这些研究只能反映停机位指派需要解决的部分问题,缺乏全局性。在算法方面,大部分学者采用遗传算法、模拟退火算法或者禁忌搜索算法等对停机位指派模型进行求解,虽然求解速度通常比较快,但是无法进行多目标共同求解。在实际的停机位指派过程中,需要平衡航空公司、机场和旅客的三方利益,使得指派结果的综合效能最大化,同时对多目标模型进行有效的求解。
1 模型建立 1.1 模型假设(1) 停机位指派是一个连续运行过程,本文选取高峰期内某一时段航班为研究对象。
(2) 停机位数量满足该时段内所有航班需求,即每架航空器均能指派到一个停机位。
(3) 本文研究的停机位指派对象为航班对(以下简称航班),即由同一架航空器执行的进离港两个航班指派到同一个停机位上,且用同一个航班号表示。
(4) 研究时段内的所有航班信息已知,包括航班计划、航空器基本信息和停机位使用情况等。
(5) 对于固定的停机位,航班从停机位到跑道的出入口距离为定值,且为已知数据。
1.2 符号定义F为航班集合,F={f1, f2, …, fm},m为研究时段内航班总数,fi(1≤i≤m)为航班对代号,以航班进港时间由早到晚进行排序,即i越大航班fi的进港时间越晚。
cfi为执行航班fi的航空器大小,cfi越大,表示航空器越大,cfi越小,表示航空器越小;例如:将中型航班标准化为cfi=1,小型航班取为cfi=0.6cfi,大型航班取为cfi=1.2cfi。
L为航空公司集合,L= {l1, l2, …, lq},q为研究时段内航空公司总数,la(1≤a≤q)为航空公司。
Fla为la航空公司的航班集合。
G为停机位集合,G= {g1, g2, …, gn},n是研究范围内的停机位总数,gk(1≤k≤n)表示停机位。
cgk为停机位gk的类型,cgk越大,表示可停放的航空器越大,cgk越小,表示可停放的航空器越小。
例如:将中型停机位标准化为cgk=1,小型停机位取为cgk=0.6cgk,大型停机位取为cgk=1.2cgk。
| $ {X_{{g_k}}} = \left\{ \begin{array}{l} 1,\;\;\;停机位\;{g_k}\;为近机位;\\ 0,\;\;\;远机位。\end{array} \right. $ |
afi为航班fi的计划进港时间,单位为min。
dfi为航班fi的计划离港时间,单位为min。
tfi为航班fi的停机位占用时间,与本文定义的航班过站时间相同,tfi=dfi-afi,单位为min。
afi'为航班fi的实际进港时间,单位为min。
dfi'为航班fi的实际离港时间,单位为min。
b为同一停机位上连续两个航班之间的缓冲时间,即停机位为航班fi服务的实际时间区间为[afi'-b, dfi'+b],单位为min。
T为同一停机位上两个航班的最小时间间隔,单位为min。
Sgkarr为航空器从跑道出口滑行到停机位gk的距离。
Sgkdep为航空器从停机位gk滑行到跑道入口的距离。
Sgka为进港旅客从停机位gk到行李大厅的距离。
Sgkd为离港旅客从安检点到停机位gk的距离。
Sgkm为旅客从停机位gk步行到中转柜台的距离。
Nfia为航班fi进港旅客数量。
Nfid为航班fi离港旅客数量。
Nfim为航班fi的中转旅客数量。
v为航空器在飞行区的平均滑行速度,取v=15 km/h。
COSTfi为航班fi单位时间内滑行的油耗成本。
COSTfi, gk为航班fi指派到停机位gk产生的停机成本。
| $ {y_{{f_i},{g_k}}} = \left\{ \begin{array}{l} 1,\;\;\;航班\;{f_i}\;分配到停机位\;{g_k};\\ 0,\;\;\;其他。\end{array} \right. $ |
| $ {z_{{f_i},{f_j}}} = \left\{ \begin{array}{l} 1,\;\;\;航班\;{f_i},{f_j}\;分配到同一个机位;\\ 0,\;\;\;其他。\end{array} \right. $ |
M为一个足够大的值。
1.3 模型建立(1) 目标函数
航空公司运行过程中,要尽力降低航空器运行成本和停机成本。航空器运行成本往往受到诸如恶劣天气、事故等不可控因素的影响较多,往往难以控制。而停机成本则受到指派效率、指派公平性等因素影响较多,通过有效的管理可以大大降低航空器停机成本。
根据中国民用航空局2007年颁布的《民用机场收费改革实施方案》中的停机位收费标准和指派原则,建立最小化航空器停机位指派目标函数为
| $ \begin{array}{*{20}{c}} {\min {Z_1} = \sum\limits_{{f_i} \in F} {\sum\limits_{{g_i} \in G} {{y_{{f_i},{g_k}}}} } \times }\\ {\left[ {\frac{{\left( {S_{{g_k}}^{{\rm{arr}}} + S_{{g_k}}^{{\rm{dep}}}} \right)}}{v} \times {\rm{COS}}{{\rm{T}}_{{f_i}}} + {\rm{COS}}{{\rm{T}}_{{f_i},{g_k}}}} \right]} \end{array} $ | (1) |
计算方式为
| $ \begin{array}{l} {\rm{COS}}{{\rm{T}}_{{f_i},{g_k}}} = \\ \left\{ \begin{array}{l} 50\left[ {\frac{{{t_{{f_i}}} + 29}}{{30}}} \right]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t_{{f_i}}} \le 240\;\min ,{X_{{g_k}}} = 1\\ 55 \times 2{c_{{f_i}}} + 45\left[ {\frac{{{t_{{f_i}}} + 59}}{{60}}} \right]\;\;\;\;\;\;{t_{{f_i}}} \le 240\;\min ,{X_{{g_k}}} = 0\\ 55 \times 2{c_{{f_i}}} + 45 \times 2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t_{{f_i}}} > 240\;\min ,{X_{{g_k}}} = 0 \end{array} \right. \end{array} $ |
从旅客的角度,停机位指派的主要目的是提高旅客满意度。以最小化旅客步行距离为目标建立停机位指派目标函数为
| $ \min {Z_2} = \sum\limits_{{f_i} \in F} {\sum\limits_{{g_k} \in G} {{y_{{f_i},{g_k}}}\left( {N_{{f_i}}^{\rm{a}}S_{{g_k}}^{\rm{a}} + N_{{f_i}}^{\rm{d}}S_{{g_k}}^{\rm{d}} + N_{{f_i}}^{\rm{m}}S_{{g_k}}^{\rm{m}}} \right)} } $ | (2) |
从机场的角度,停机位指派的主要目的是提高预指派计划的抗干扰能力,以最小化航班指派发生冲突概率为目标建立停机位指派目标函数为
| $ \min {Z_3} = \sum\limits_{{f_i},{f_j} \in F,i < j} {\left( {{z_{{f_i},{f_j}}} \times P\left( {{f_i},{f_j}} \right)} \right)} $ | (3) |
式中:P(fi, fj)为航班fi和航班fj之间发生冲突的概率,且
| $ P\left( {{f_i},{f_j}} \right) = \frac{{e\left( {{f_i},{f_j}} \right) - \min \left\{ {e\left( {{f_i},{f_j}} \right)} \right\}}}{{\max \left\{ {e\left( {{f_i},{f_j}} \right)} \right\} - \min \left\{ {e\left( {{f_i},{f_j}} \right)} \right\}}} $ |
式中:e(fi, fj)可以是反函数、线性函数、余弦函数或指数函数,本文中根据实际情况在仿真中选用指数函数,即e(fi, fj)=e(-γl(fi, fj)),其中γ为一个常数,用于控制曲率,根据实际情况,此处取为γ=0.03[16]。
根据停机位指派的多目标函数可知,停机位指派结果将对大型航空器的停机位指派更为有利,这对拥有小型航空器较多的航空公司极不公平。本文通过增加“公平性”函数调整停机位指派结果的公平性。分别以航空公司航班的平均滑行距离和机场所有航空器平均滑行距离的差值与所有航空器平均滑行距离的比值最小、航空公司的所有旅客平均步行距离和机场所有航空器旅客平均步行距离差值与所有航空器旅客平均步行距离比值最小为目标,建立停机位指派目标函数为
| $ \min {Z_4} = \frac{{\left| {{{\bar S}_{{l_a}}} - \bar S} \right|}}{{\bar S}}\;\;\;\;\;{l_a} \in L $ | (4) |
| $ \min {Z_5} = \frac{{\left| {{{\bar W}_{{l_a}}} - \bar W} \right|}}{{\bar W}}\;\;\;\;\;{l_a} \in L $ | (5) |
式中:Sla为航空公司la的航班平均滑行距离,S为机场所有航班的平均滑行距离,Wla为la航空公司旅客平均步行距离,W为所有旅客平均步行距离。
| $ {{\bar S}_{{l_a}}} = \frac{{\sum\limits_{{f_i} \in {F_{{l_a}}}} {\sum\limits_{{g_k} \in G} {{y_{{f_j},{g_k}}} \times \left( {S_{{g_k}}^{{\rm{arr}}} + S_{{g_k}}^{{\rm{dep}}}} \right)} } }}{{\left| {{F_{{l_a}}}} \right|}} $ |
| $ \bar S = \frac{{\sum\limits_{{f_i} \in F} {\sum\limits_{{g_k} \in G} {{y_{{f_i},{g_k}}} \times \left( {S_{{g_k}}^{{\rm{arr}}} + S_{{g_k}}^{{\rm{dep}}}} \right)} } }}{{\left| F \right|}} $ |
| $ {{\bar W}_{{l_a}}} = \frac{{\sum\limits_{{f_i} \in F} {\sum\limits_{{g_k} \in G} {{y_{{f_i},{g_k}}}\left( {N_{{f_i}}^{\rm{a}}S_{{g_k}}^{\rm{a}} + N_{{f_i}}^{\rm{d}}S_{{g_k}}^{\rm{d}} + N_{{f_i}}^{\rm{m}}S_{{g_k}}^{\rm{m}}} \right)} } }}{{\sum\limits_{{f_i} \in {F_{{l_a}}}} {\left( {N_{{f_i}}^{\rm{a}} + N_{{f_i}}^{\rm{d}} + N_{{f_i}}^{\rm{m}}} \right)} }} $ |
| $ \bar W = \frac{{\sum\limits_{{f_i} \in F} {\sum\limits_{{g_k} \in G} {{y_{{f_i},{g_k}}}\left( {N_{{f_i}}^{\rm{a}}S_{{g_k}}^{\rm{a}} + N_{{f_i}}^{\rm{d}}S_{{g_k}}^{\rm{d}} + N_{{f_i}}^{\rm{m}}S_{{g_k}}^{\rm{m}}} \right)} } }}{{\sum\limits_{{f_i} \in {F_{{l_a}}}} {\left( {N_{{f_i}}^{\rm{a}} + N_{{f_i}}^{\rm{d}} + N_{{f_i}}^{\rm{m}}} \right)} }} $ |
(2) 约束条件
| $ \sum\limits_{{g_k} \in G} {{y_{{f_i},{g_k}}}} = 1\;\;\;\;\forall {f_i} \in F $ | (6) |
| $ {y_{{f_i},{g_k}}} \in \left\{ {0,1} \right\} $ | (7) |
式(6)和(7)为航班指派唯一性约束。即每个航班能且仅能指派一个停机位。
| $ \sum\limits_{{g_k} \in G,{X_{{g_k}}} = 0} {{y_{{f_i},{g_k}}}} = 1\;\;\;\;\forall {f_i} \in F,{T_{{f_i}}} > 240 $ | (8) |
式(8)表示过站时间超过4 h的航班均指派到远机位。
| $ {y_{{f_i},{g_k}}} \times {y_{{f_j},{g_k}}} \times \left( {{d_{{f_i}}} - {a_{{f_j}}}} \right) \times \left( {{d_{{f_j}}} - {a_{{f_i}}}} \right) \le 0 $ | (9) |
式(9)可以确保同一停机位上没有同时指派两个航班
| $ {z_{{f_i},{f_j}}} = \sum\limits_{{f_i} \in f} {\sum\limits_{j > i,{f_j} \in F} {\sum\limits_{{g_k} \in G} {\left( {{y_{{f_i},{g_k}}} \times {y_{{f_j},{g_k}}}} \right)} } } $ | (10) |
| $ {a_{{f_j}}} - {d_{{f_i}}} + \left( {1 - {z_{{f_i},{f_j}}}} \right)M \ge T\;\;\;\;i < j $ | (11) |
式(10)和(11)表示同一停机位上的两个航班应满足一定的安全时间间隔。其中,M为一个足够大的值
| $ \begin{array}{*{20}{c}} {{c_{{f_i}}} \le {c_{{g_k}}} + \left( {1 - {y_{{f_i},{g_k}}}} \right)M}\\ {i,j,k,a \in {{\bf{Z}}^ + }} \end{array} $ | (12) |
式(12)表示停机位和机型必须匹配或停机位可停放的航空器大小大于停放的航空器大小。
2 基于NSGA-Ⅱ算法的停机位多目标指派仿真验证第2代非支配排序遗传算法(Non-dominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ)是由第1代非支配排序遗传算法优化得到的,也是一种针对多目标优化问题得到非支配解集的算法。首先进行种群的初始化,然后对种群中的个体进行快速非支配排序,接下来,以此前进行的非支配排序和拥挤度排序的结果为运行基础进行选择操作,与此同时对种群内的个体进行交叉和变异操作。该算法与遗传算法的最大区别在于NSGA-Ⅱ算法中增加了快速非支配排序和拥挤度排序的过程。
本文将航空器分为大、中、小3类,选取中国某大型机场为仿真对象。根据各机型运行性能数据,设定滑行油耗为:大型航空器40 kg/min,中型航空器22 kg/min,小型航空器12 kg/min。航油价格取7 500元/t。选取中国某大型机场5:00至20 :00待指派停机位的国内航班57组相关数据为研究对象,G000~G006为7个近机位,G007~G 00 9为3个远机位,默认远机位可以无限制停放。具体航班信息来源于厦门高崎国际机场2015年9月某工作日从8:00至14:00的航班和停机位数据,因篇幅原因未列出。
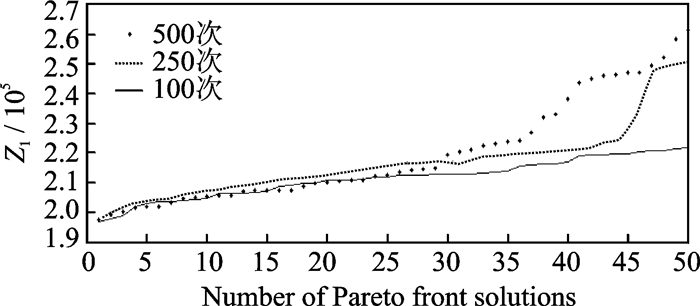
停机位优化指派模型中,取航空器的平均滑行速度v=15 km/h,最短时间间隔参数T=15 min,M=700。其中,Z1,Z2,Z3,Z4和Z5分别表示目标函数(1—5)的值。采用NSGA-Ⅱ算法对5个目标函数同时进行求解,对目标函数进行求解的演变过程如图 1—5所示。
|
图 1 目标函数Z1与迭代次数的关系 Figure 1 Relationship between objectivefunction Z1 and number of iterations |
|
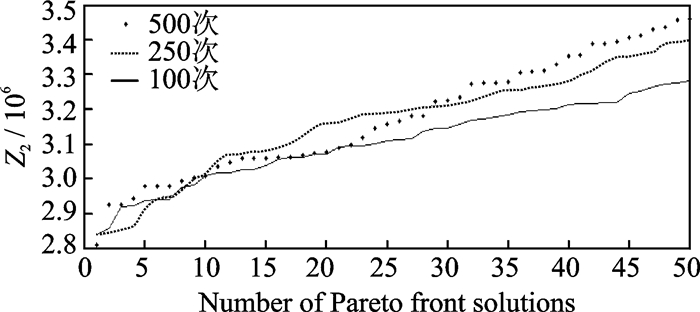
图 2 目标函数Z2与迭代次数的关系 Figure 2 Relationship between objective function Z2 and number of iterations |
|
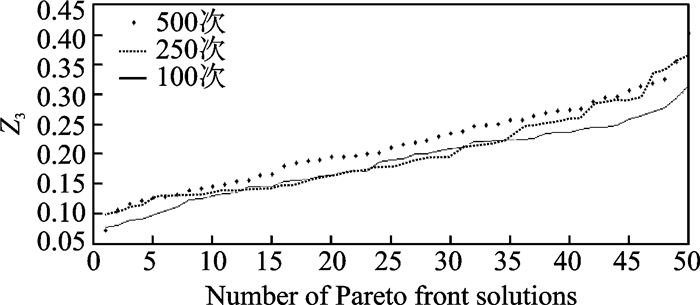
图 3 目标函数Z3与迭代次数的关系 Figure 3 Relationship between objectivefunction Z3 and number of iterations |
|
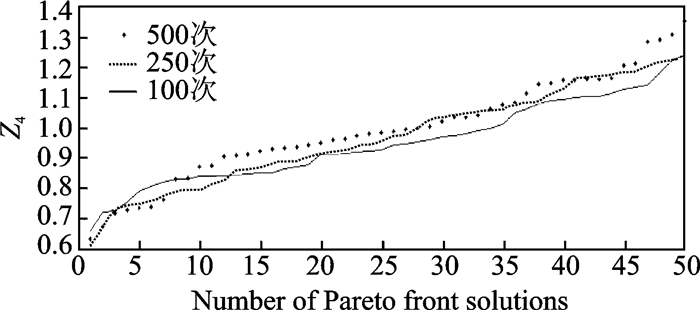
图 4 目标函数Z4与迭代次数的关系 Figure 4 Relationship between objectivefunction Z4 and number of iterations |
|
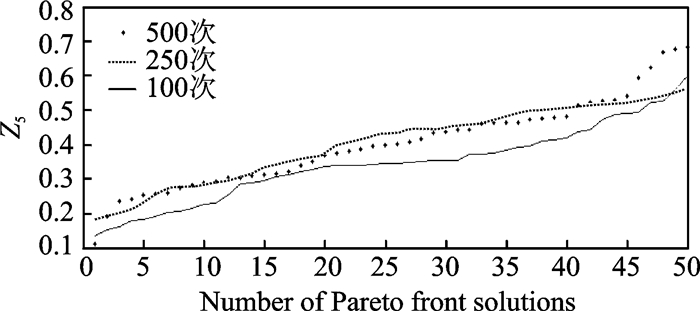
图 5 目标函数Z5与迭代次数的关系 Figure 5 Relationship between objective function Z5 and number of iterations |
图 1—5中,横坐标为Pareto前沿解的个数,每一次迭代均按照数值升序取前50个解,纵坐标分别为5个目标函数,3条曲线分别表示迭代100次, 250次, 500次所获得的Pareto前沿解的取值。随着迭代次数的增加,所获得Pareto前沿解的目标函数值都在减小,这说明NSGA-Ⅱ算法得到的解的质量在不断提高。通过不断迭代求解,求解结果在航空公司运行成本、旅客总步行距离、调度计划鲁棒性以及航空公司公平性上的表现都有所提高。以Pareto前沿解为基础单位,研究求解每个函数单位的数值特征,分析不同迭代次数下所得Pareto前沿解集所有解的平均值、中位值、最大值和最小值的变化。具体趋势如图 6—10所示,纵坐标为Pareto解集关于目标函数的数值特征,横坐标为迭代次数。
|
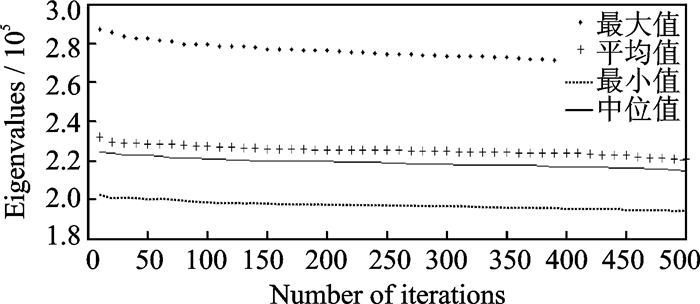
图 6 目标函数Z1的特征值与迭代次数的关系 Figure 6 Relationship between eigen valuesof objective Z1 and number of iterations |
|
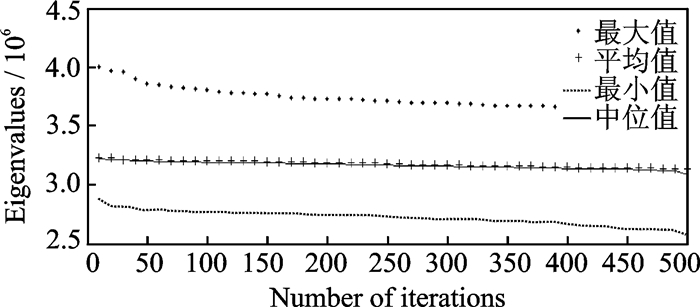
图 7 目标函数Z2的特征值与迭代次数的关系 Figure 7 Relationship between eigenvalues of objective Z2 and number of iterations |
|
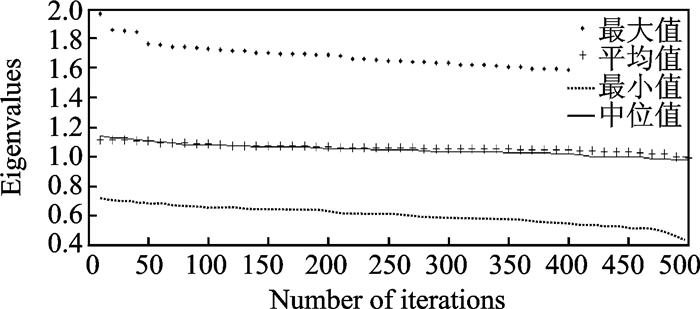
图 8 目标函数Z3的特征值与迭代次数的关系 Figure 8 Relationship between the eigenvalues of objective Z3 and number of iterations |
|
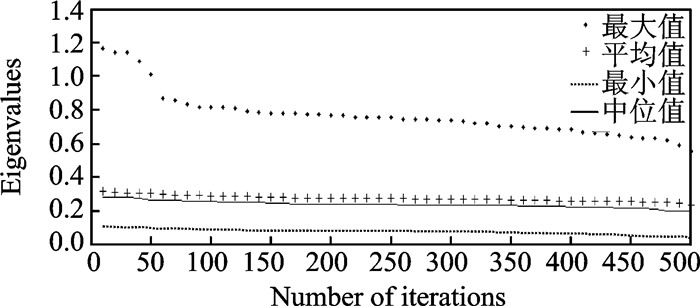
图 9 目标函数Z4的特征值与迭代次数的关系 Figure 9 Relationship between the eigenvalues of objective Z4 and the number of iterations |
|
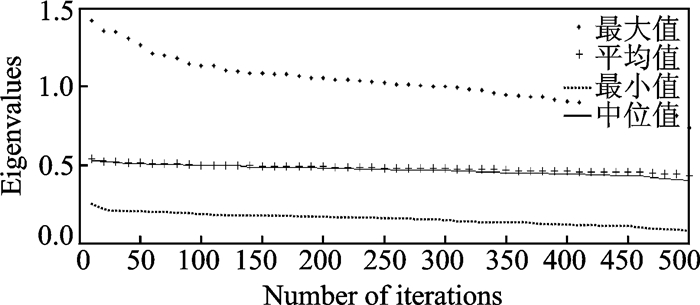
图 10 目标函数Z5的特征值与迭代次数的关系 Figure 10 Relationship between the eigenvalues of objective Z5 and the number of iterations |
从图 6—10可以看出,其纵坐标依次为5个目标函数,横坐标为迭代次数,4种不同的曲线分别表示某迭代次数下得到的所有Pareto前沿解关于不同目标函数的数值特征值,包括最大值、平均值、最小值和中位数。随着迭代次数的增加,每一代Pareto解集中所有解的目标函数值的平均值、中位数、最大值和最小值都在不断减小,即通过NSGA-Ⅱ算法得到的解的目标值的整体变化趋势在不断减小,且整组数据的波动没有变大,可以保证所得数值的公平性并且减小偶然性,可见所得Pareto解集中的解的整体质量在不断提高。另分析5组图片,发现每组数据中的中位值都略小于平均值,说明整组数据呈现右偏分布。表 1是迭代500次的Pareto前沿解和人工指派结果比较,验证了本模型对停机位指派问题进行优化的程度。
| 表 1 迭代500次的Pareto前沿解和人工指派结果比较 Table 1 Comparison of Pareto frontier solutions and artificial assignment results for 500 iterations |
表 1中已将迭代500次的各个解中的侧重目标函数值加黑标出。在最终得到的所有Pareto前沿解中,分别取Z1,Z2,Z3,Z4,Z5值最小的5个解,将其与人工指派结果进行比较,可见经过NSGA-Ⅱ算法优化的结果总体大大优于随机指派的结果。随机指派的每个目标值都明显差于经过500次迭代的优化解,经过迭代,解的质量已经明显提高。除此之外,还可以根据需求对NSGA-Ⅱ算法得到的Pareto解集中的解进行人工选择,使得最终得到的解更符合实际需求。
3 结束语本文从航空公司、机场和旅客三方角度出发,旨在寻找航空公司运行成本、旅客步行距离和航班冲突概率综合最小化的停机位指派方案,兼顾航空公司之间的公平性,寻求指派结果综合效能最大化。提出了一种满足三方利益的停机位指派模型,采用NSGA-Ⅱ算法对模型进行求解,具有突出的优化性能,可以为机场的停机位指派决策提供参考。NSGA-Ⅱ算法不是简单地按对多个目标进行分配权重的方法进行求解,而是对5个目标同时进行求解,因此对NSGA-Ⅱ算法的求解结果与不同算法下单目标的优化结果进行比较可以作为接下来的研究方向。
| [1] |
LIM A, RODRIGUES B, ZHU Y.
Airport gate scheduling with time windows[J]. Artificial Intelligence Review, 2005, 24(1): 5–31.
|
| [2] |
SEKER M, NOYAN N.
Stochastic optimization models for the airport gate assignment Problem[J]. Transportation Research Part E Logistics & Transportation Review, 2012, 48(2): 438–459.
|
| [3] |
熊杰, 张晨.
基于飞机滑行油耗的枢纽机场机位分配研究[J]. 交通运输系统工程与信息, 2010, 10(3): 165–170.
DOI:10.3969/j.issn.1009-6744.2010.03.028 XIONG Jie, ZHANG Chen. Airport gate assignment with airplane taxiing cost analysis[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(3): 165–170. DOI:10.3969/j.issn.1009-6744.2010.03.028 |
| [4] |
DIEPEN G, AKKER J M V D, HOOGEVEEN J A, et al.
Finding a robust assignment of flights to gates at Amsterdam airport schiphol[J]. Journal of Scheduling, 2012, 15(6): 703–715.
DOI:10.1007/s10951-012-0292-y
|
| [5] |
MAHARJAN B, MATIS T I.
Multi-commodity flow network model of the flight gate assignment problem[J]. Computers & Industrial Engineering, 2012, 63(4): 1135–1144.
|
| [6] |
JIANG Y, ZENG L, LUO Y.
Multiobjective gate assignment based on passenger walking distance and fairness[J]. Mathematical Problems in Engineering, 2013(7): 717–718.
|
| [7] |
DORNDORF U, JAEHN F, PESCH E.
Flight gate scheduling with respect to a reference schedule[J]. Annals of Operations Research, 2012, 194(1): 177–187.
DOI:10.1007/s10479-010-0809-8
|
| [8] |
NIKULIN Y, DREXL A.
Theoretical aspects of multicriteria flight gate scheduling:Deterministic and fuzzy models[J]. Journal of Scheduling, 2010, 13(3): 261–280.
DOI:10.1007/s10951-009-0112-1
|
| [9] |
PREM K V, BIERLAIRE M.
Multi-objective airport gate assignment problem in planning and operations[J]. Journal of Advanced Transportation, 2014, 48(7): 902–926.
DOI:10.1002/atr.v48.7
|
| [10] |
杨文东, 朱金福, 许俐.
基于航班连结树的机场停机位指派问题研究[J]. 山东大学学报(工学版), 2010, 40(2): 153–158.
YANG Wendong, ZHU Jinfu, XU Li. Research on the gate assignment problem in airport based on the flight connecting tree[J]. Journal of Shandong University(Engineering Science), 2010, 40(2): 153–158. |
| [11] |
王笑天, 田勇, 万莉莉, 等.
基于列生成算法的停机位指派的鲁棒性研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(1): 171–174.
DOI:10.3963/j.issn.2095-3844.2015.01.039 WANG Xiaotian, TIAN Yong, WAN Lili, et al. Research on robustness of gate assignment based on column generation methods[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2015, 39(1): 171–174. DOI:10.3963/j.issn.2095-3844.2015.01.039 |
| [12] |
解英全.基于遗传蚁群混合算法的机场停机位分配研究[D].西安: 西安工业大学, 2015.
XIE Yingquan. Aircraft stand assignment research based on genetic ant colony hybrid algorithm[D]. Xi'an: Xi'an Technological University, 2015. |
| [13] |
GENC H M, EROL O K, IBRAHIM E, et al.
A stochastic neighborhood search approach for airport gate assignment problem[J]. Expert Systems with Applications, 2012, 39(1): 316–327.
DOI:10.1016/j.eswa.2011.07.021
|
| [14] |
WANG H, LUO Y, SHI Z.
Real-time gate reassignment based on flight delay feature in hub airport[J]. Mathematical Problems in Engineering, 2013, 18(5): 708–716.
|
| [15] |
LIU J Q, ZHANG M L, CHEN P C, et al.
An integrative approach with sequential game to real-time gate assignment under CDM mechanism[J]. Mathematical Problems in Engineering, 2014, 25(1): 172–181.
|
| [16] |
曾琳燕.大型机场停机位多目标指派研究[D].南京: 南京航空航天大学, 2014.
ZENG Linyan. Study on large airport multi-objective gate assignment[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. |
 2018, Vol. 50
2018, Vol. 50


