2. 武警后勤学院学兵二大队九队, 天津, 300309
2. Student 2 Brigade 9 Teams, Logistics University of PAP, Tianjin, 300309, China
倾转旋翼机是一种将固定翼飞机和直升机特点融为一体的新型飞行器,其显著提升了直升机和固定翼飞机的使用范围,在军用和民用领域具有广泛的应用前景。由于倾转旋翼机在起飞着陆过程中的动能和势能较低,而需用功率较高,若遭遇发动机失效,驾驶员不恰当的操纵很可能造成飞行事故,因此研究倾转旋翼机在起飞着陆时发动机失效后的最优轨迹和操纵过程对飞行安全具有重要的意义。
飞行试验是检验倾转旋翼机发动机单发失效后如何操纵飞行器安全着陆的最终手段,但是飞行试验风险大、耗时且耗资。为了降低飞行试验的成本和风险,数值优化方法被提出来预测倾转旋翼机单发失效后着陆的最优操纵策略和飞行轨迹,为飞行试验提供理论依据。
倾转旋翼机单发失效后的轨迹数值优化研究始于20世纪90年代。Cerbe等[1-2]采用参数优化的方法研究了倾转旋翼机短距起飞和斜向起飞单发失效后的安全飞行问题。Carlson等[3-7]建立了倾转旋翼机纵向刚体飞行动力学模型,并应用最优控制理论研究了倾转旋翼机在短距起飞、垂直起飞时遭遇单发失效后的最优着陆轨迹和回避区。Bottasso等[8]对最优控制理论中的目标函数进行了扩展,研究了倾转旋翼机短距起飞单发失效后的继续起飞问题。然而,从以上文献的计算结果可以看出,倾转旋翼机单发失效后的最优飞行轨迹以及对应的旋翼拉力、旋翼后倒角和短舱倾转角的时间历程容易出现比较剧烈的波动现象,驾驶员难以实现对应的操纵。这是因为以上文献在研究过程中均未考虑到驾驶员反应特性的影响。由于倾转旋翼机单发失效后的着陆过程是一种机动飞行过程,驾驶员的操纵较为复杂,因此有必要在轨迹数值优化研究中考虑驾驶员的感知延迟、肌肉神经系统特性以及助力器速率限制等对驾驶员操纵以及最优轨迹的影响。
为了能在倾转旋翼机单发失效轨迹数值优化的研究中考虑到驾驶员的反应特性,本文在倾转旋翼机基本纵向刚体模型的基础上,建立旋翼拉力系数、旋翼后倒角与操纵杆量之间的关系,并引入延迟环节、惯性环节和操纵速率限制来模拟驾驶员的反应特性,形成适用于倾转旋翼机单发失效轨迹数值优化研究的增广飞行动力学模型。然后,以XV-15倾转旋翼机为例,利用最优控制理论,计算短距起飞单发失效后的最优着陆过程,并与文献[4]中的计算结果进行对比和分析。最后,本文进一步分析不同驾驶员感知延迟时间对最优轨迹和操纵策略的影响。
1 飞行动力学建模 1.1 基本飞行动力学模型倾转旋翼机具有沿纵向对称构型,在单发失效时,剩余有效发动机仍通过传动轴同时驱动着两副旋翼以相同转速工作,因此在无侧风条件下,单发失效后的飞行轨迹和与之相关的操纵都在纵向平面。为了提高计算效率,本文首先建立引入旋翼转速自由度的倾转旋翼机基本纵向刚体飞行动力学模型。其状态变量为:体轴系中的纵向速度u和垂向速度w、俯仰角速度q、俯仰角θ、旋翼转速Ω、水平位移x和高度h;控制变量为:旋翼拉力系数CT、旋翼后倒角β和短舱倾转角in。主控方程如下
| $ {{\mathit{\boldsymbol{\dot x}}}_b} = {f_b}\left( {{\mathit{\boldsymbol{x}}_b},{\mathit{\boldsymbol{u}}_b},t} \right) $ | (1) |
式中:xb=[u, w, q, θ, Ω, x, h]T;ub=[CT, β, in]T。
各部件的气动力和力矩系数均由风洞试验数据[9]插值获得。由于旋翼尾流对机翼的干扰,机翼-短舱的气动力被分为两部分:一部分为受到旋翼尾流影响的机翼气动力,另一部分为不受旋翼尾流作用的机翼气动力。机翼处于旋翼滑流部分的面积Swss和处于自由流部分的面积Swfs的计算公式分别为[4]
| $ \left\{ \begin{array}{l} {S_{{\rm{wss}}}} = {S_{{\rm{ssmax}}}}\left[ {\sin \left( {a \cdot {i_n}} \right) + \cos \left( {b \cdot {i_n}} \right)} \right]\frac{{{\mu _{\max }} - \mu }}{{{\mu _{\max }}}}\\ {S_{{\rm{wfs}}}} = {S_{\rm{w}}} - {S_{{\rm{wss}}}} \end{array} \right. $ | (2) |
式中:Sw为机翼面积;Sssmax=2ηssRc;a=1.386;b=3.114;ηss为旋翼滑流修正因子;R为旋翼半径;c为机翼平均气动弦长;μ为旋翼前进比;μmax为旋翼尾迹偏出机翼的最大前进比; in为发动机短舱倾转角。
倾转旋翼机在单发失效时,失效的发动机输出功率会逐渐衰减,为了保证倾转旋翼机能够顺利安全着陆,剩余发动机以最大可用功率输出,该过程可以表示为[4]
| $ {P_A} = \left( {{P_{{\rm{AEO}}}} - {P_{{\rm{OEI}}}}} \right){{\rm{e}}^{ - t/{\tau _{\rm{e}}}}} + {P_{{\rm{OEI}}}} $ | (3) |
式中:PAEO为两台发动机正常工作时的输出功率;POEI为单发失效后最大可用功率;τe为发动机响应时间常数。
基本纵向刚体飞行动力学模型适用于计算单发失效后伴随非定常旋翼转速变化的飞行过程,因此可用于进行倾转旋翼机单发失效后的轨迹数值优化研究。
1.2 增广飞行动力学模型由于基本飞行动力学模型没有包含驾驶员的操纵杆量信息,故无法模拟驾驶员的反应特性。因此,本节首先建立旋翼拉力系数、旋翼后倒角与操纵杆量之间的关系。
根据旋翼叶素理论[10]建立旋翼拉力系数CT和旋翼后倒角β与旋翼总距和纵向周期变距操纵的代数方程
| $ \left\{ \begin{array}{l} {C_T} - \frac{1}{2}{a_\infty }\sigma \left[ {\left( {\frac{1}{3} + \frac{1}{2}{\mu ^2}} \right){\theta _0} + \frac{1}{4}\left( {1 + {\mu ^2}} \right){\theta _1} - } \right.\\ \;\;\;\;\;\;\left. {\frac{1}{2}\lambda - \frac{1}{2}\mu {\theta _s}} \right] = 0\\ \beta - \left[ {\left( {\frac{8}{3}{\theta _0} + 2{\theta _1} - 2\lambda } \right)\mu - \left( {1 + \frac{3}{2}{\mu ^2}} \right){\theta _s} - \frac{{16}}{{{\gamma _b}}}\frac{q}{\mathit{\Omega }}} \right]/\\ \;\;\;\;\;\;\;\left( {1 - \frac{1}{2}{\mu ^2}} \right) = 0 \end{array} \right. $ | (4) |
式中:α∞为升力线斜率;σ为旋翼实度;μ为前进比;λ为入流比;θ0为旋翼桨根总距;θ1为桨叶扭度;θs为纵向周期变距;γb为桨叶洛克数。
以XV-15倾转旋翼机为例,将驾驶员操纵加入到模型中,驾驶员通过总距杆位移δcol改变旋翼桨根总距θ0,通过纵向杆位移δlon改变纵向周期变距θs和升降舵偏转角θe,并通过拇指滚轮δin来改变发动机短舱倾转角in。直升机模式下,周期变距和总距的操纵与常规直升机的操纵相同,但是当短舱倾转角in逐渐减小(由直升机模式变为固定翼模式)时,纵向周期变距操纵和总距操纵效能逐渐减弱,直至短舱倾转角in=0°时消失。这个过程可以用以下公式表示[9]
| $ \left\{ \begin{array}{l} {\theta _s} = \left( {2 \cdot {\delta _{{\rm{lon}}}} - 1} \right) \cdot {\theta _{s\max }}\sin {i_n} + {\delta _{B1}}\left( {1 - \sin {i_n}} \right)\\ {\theta _e} = {\theta _{e\max }} \cdot {\delta _{{\rm{lon}}}}\\ {\theta _0} = \partial {\theta _0}/\partial {\delta _{{\rm{col}}}} \cdot {\delta _{{\rm{col}}}} + {\theta _{0L}} + {\theta _{0RG}}\\ {i_n} = {\delta _{in}} \end{array} \right. $ | (5) |
式中:θsmax为最大纵向周期变距;补偿量δB1为1.5°;θemax为最大升降舵偏转角;θ0RG为旋翼转速调节系统输出的总距补偿量;倾转旋翼机在不同短舱倾转角下有对应的∂θ0/∂δcol与θ0L,因此旋翼桨根总距θ0可以通过多项式拟合表示为in,δcol和θ0RG的函数
| $ \begin{array}{l} {\theta _0} = \left[ {\left( {3.045\;9i_n^4 + 6.470\;7i_n^3 - 2.394\;2i_n^2 + } \right.} \right.\\ \;\;\;\;\;\;\;\left. {9.815\;6{i_n}} \right){\delta _{{\rm{col}}}} + \left( {6.510\;8i_n^3 - 13.849i_n^2 - } \right.\\ \;\;\;\;\;\;\;\left. {9.386{i_n} + 52.125} \right] \cdot {\rm{ \mathsf{ π} }}/180 + {\theta _{0RG}} \end{array} $ | (6) |
式(5)和(6)适用于倾转旋翼机的全部飞行模式,也适用于倾转旋翼机单发失效后的旋翼桨根总距操纵[9]。
在倾转旋翼机单发失效后的着陆过程中,驾驶员从感知到决策再到操纵量实际发生变化之间会有一定的延迟,且驾驶员在操纵时也会受到肌肉神经系统特性以及倾转旋翼机的助力器速率限制的影响。为了模拟以上驾驶员反应特性,本文首先分别对3个操纵量通道引入可以反映出倾转旋翼机驾驶员感知延迟和肌肉神经系统特性的延迟环节和惯性环节[11-12]
| $ \frac{{{\mathit{\boldsymbol{u}}_{\rm{p}}}\left( s \right)}}{{\mathit{\boldsymbol{u}}\left( s \right)}} = \frac{1}{{{T_{\rm{p}}}s + 1}}{{\rm{e}}^{ - {\tau _{\rm{p}}}s}} $ | (7) |
式中:τp为驾驶员感知延迟时间,即驾驶员从感知到决策再到操纵量实际发生变化之间的时间;Tp为驾驶员神经肌肉滞后时间常数。
纯延迟环节e-τps可用一阶Pade逼近
| $ {{\rm{e}}^{ - {\tau _{\rm{p}}}s}} \approx \frac{{1 - {\tau _{\rm{p}}}s}}{{1 + {\tau _{\rm{p}}}s}} $ | (8) |
分别对3个操纵量通道引入式(7), (8),并转化为微分方程形式
| $ \left\{ \begin{array}{l} {{\dot x}_{{\rm{lon}}}} = \frac{1}{{{T_{\rm{p}}}}}\left( {{u_{{\rm{lon}}}} - {x_{{\rm{lon}}}}} \right)\\ {{\dot \delta }_{{\rm{lon}}}} = \frac{1}{{{\tau _{\rm{p}}}}}\left[ { - {\delta _{{\rm{lon}}}} + \left( {{x_{{\rm{lon}}}} + {\tau _{\rm{p}}}{{\dot x}_{{\rm{lon}}}}} \right)} \right]\\ {{\dot x}_{{\rm{col}}}} = \frac{1}{{{T_{\rm{p}}}}}\left( {{u_{{\rm{col}}}} - {x_{{\rm{col}}}}} \right)\\ {{\dot \delta }_{{\rm{col}}}} = \frac{1}{{{\tau _{\rm{p}}}}}\left[ { - {\delta _{{\rm{col}}}} + \left( {{x_{{\rm{col}}}} - {\tau _{\rm{p}}}{{\dot x}_{{\rm{col}}}}} \right)} \right]\\ {{\dot x}_{{\rm{in}}}} = \frac{1}{{{T_{\rm{p}}}}}\left( {{u_{{\rm{in}}}} - {x_{{\rm{in}}}}} \right)\\ {{\dot \delta }_{{\rm{in}}}} = \frac{1}{{{\tau _{\rm{p}}}}}\left[ { - {\delta _{{\rm{in}}}} + \left( {{x_{{\rm{in}}}} - {\tau _{\rm{p}}}{{\dot x}_{{\rm{in}}}}} \right)} \right] \end{array} \right. $ | (9) |
式中:δcol,δlon和δin分别为驾驶员最后输出的操纵量。
在此基础上,本文根据倾转旋翼机的助力器速率限制[9]对式(9)中的驾驶员操纵速率
| $ \left\{ \begin{array}{l} {{\dot \delta }_{{\rm{colmin}}}} \le {{\dot \delta }_{{\rm{col}}}} \le {{\dot \delta }_{{\rm{colmax}}}}\\ {{\dot \delta }_{{\rm{lonmin}}}} \le {{\dot \delta }_{{\rm{lon}}}} \le {{\dot \delta }_{{\rm{lonmax}}}}\\ {{\dot \delta }_{{\rm{inmin}}}} \le {{\dot \delta }_{{\rm{in}}}} \le {{\dot \delta }_{{\rm{inmax}}}} \end{array} \right. $ | (10) |
式(9), (10)可以用于模拟倾转旋翼机单发失效后驾驶员的反应特性。
倾转旋翼机在单发失效后的着陆过程是一种机动飞行过程,为便于驾驶员操纵,一般选择关闭控制增稳系统和旋翼转速调节系统[4]。式(1), (4), (9)组成了增广飞行动力学模型的主控方程,其状态变量为:u, w, q, θ, Ω, x, h, xcol, δcol, xlon, δlon, xin, δin;代数变量为:CT, β;控制变量为:ucol, ulon和uin。
令
| $ \begin{array}{l} \mathit{\boldsymbol{x}} = {\left[ {u,w,q,\theta ,\mathit{\Omega },x,h,{x_{{\rm{col}}}},{\delta _{{\rm{col}}}},{x_{{\rm{lon}}}},{\delta _{{\rm{lon}}}},{x_{{\rm{in}}}},{\delta _{{\rm{in}}}}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{a}} = {\left[ {{C_T},\beta } \right]^{\rm{T}}}\\ \mathit{\boldsymbol{u}} = {\left[ {{u_{{\rm{col}}}},{u_{{\rm{lon}}}},{u_{{\rm{in}}}}} \right]^{\rm{T}}} \end{array} $ | (11) |
则增广飞行动力学模型可表示为以下微分-代数方程组
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{a}},\mathit{\boldsymbol{u}},\mathit{\boldsymbol{t}}} \right)\\ \mathit{\boldsymbol{a}} - g\left( \mathit{\boldsymbol{x}} \right) = {\bf{0}} \end{array} \right. $ | (12) |
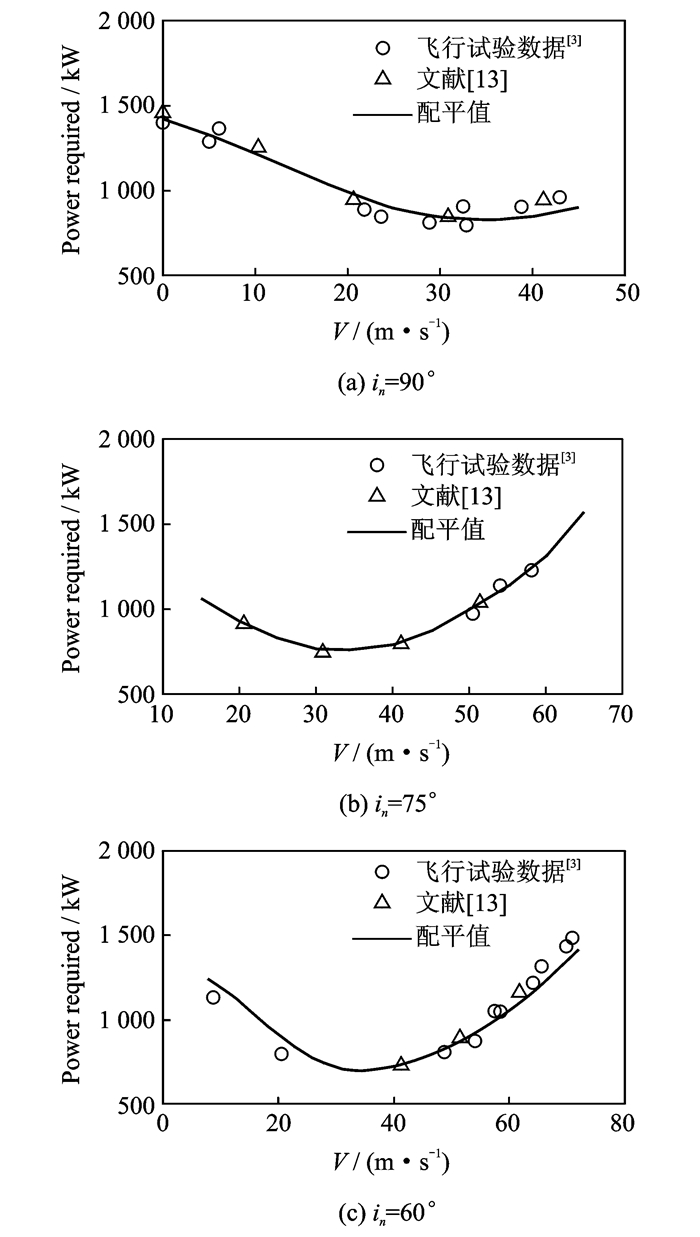
本文假设倾转旋翼机在单发失效前处于稳定飞行状态,因此需要首先计算平衡状态,为接下来的动态轨迹优化过程提供初始值。本文根据公式(12)的配平结果求得旋翼需用功率,并分别与使用相同机型参数的文献[13]的理论计算数据以及XV-15的飞行试验数据[3]进行对比(图 1),所用机型质量为5 897 kg,襟翼/副翼配置40°/25°。从图 1可以看出,本文计算的需用功率和文献[13]的理论计算数据以及XV-15的飞行试验数据吻合得较好,说明本文建立的模型较为准确。
2 最优控制问题和数值解法 2.1 最优控制问题
倾转旋翼机单发失效后的最优安全着陆问题,可以归结为一种含有状态和控制约束的非线性最优控制问题。最优控制问题一般可表示成如下Bolza形式:
优化变量:状态变量x、代数变量a、控制变量u和可变的末端时刻tf。
目标函数为
| $ \begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{u}} J = \phi \left( {\mathit{\boldsymbol{x}}\left( {{t_0}} \right),{t_0},\mathit{\boldsymbol{x}}\left( {{t_f}} \right),{t_f}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{t_f} - {t_0}}}\int_{{t_0}}^{{t_f}} {L\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right),t} \right){\rm{d}}t} \end{array} $ | (13) |
式中:t0为最优控制问题的初始时刻。
约束条件:包括微分方程约束、初始边界条件、末端边界条件和路径约束。其中微分方程约束为主控方程(12)中的微分方程为
| $ \mathit{\boldsymbol{\dot x}} = f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{a}},\mathit{\boldsymbol{u}},t} \right) $ | (14) |
初始边界条件:适航管理条例FAR[14]规定运输类旋翼飞行器在单发失效时驾驶员至少要有1 s的反应时间。假设飞行器于0时刻单发失效,通过积分可得驾驶员延迟1 s(t0=1 s)后对应的飞行状态量xdelay,则t0时刻初始边界条件为
| $ \mathit{\boldsymbol{x}}\left( {{t_0}} \right) = {\mathit{\boldsymbol{x}}_{{\rm{delay}}}} $ | (15) |
在驾驶员延迟时间内,旋翼转速调节系统仍处于开启状态,本文通过一个线性反馈控制律来模拟其转速调节作用[4]为
| $ \mathit{\dot {\bar \Omega} } - K\left( {\mathit{\bar \Omega } - 1} \right) = 0 $ | (16) |
式中:K=12/(k4Ω0),为反馈增益。随后驾驶员开始操纵,此时选择关闭旋翼转速调节系统,从而可以有效利用旋翼转动储存的能量,提高安全性。
末端边界条件和路径约束可根据FAR关于旋翼类飞行器单发失效后安全着陆的具体要求确定
| $ {\mathit{\boldsymbol{x}}_{f\min }} \le \mathit{\boldsymbol{x}}\left( {{t_f}} \right) \le {\mathit{\boldsymbol{x}}_{f\max }} $ | (17) |
| $ {\mathit{\boldsymbol{x}}_{\min }} \le \mathit{\boldsymbol{x}}\left( t \right) \le {\mathit{\boldsymbol{x}}_{\max }} $ | (18) |
驾驶员操纵速率
| $ \mathit{\boldsymbol{a}} - g\left( \mathit{\boldsymbol{x}} \right) = {\bf{0}} $ | (19) |
在进行轨迹优化数值计算时,由于状态变量和控制变量的量纲不同,某些变量之间的数量级相差较大,会引起数值求解困难。所以在数值计算前,首先对飞行动力学模型中的参数进行量纲一缩放。
定义常数k1, k2, k3, k4对状态量和时间进行量纲一缩放
| $ \begin{array}{l} \bar w = \frac{{{k_1}w}}{{{\mathit{\Omega }_0}R}},\bar u = \frac{{{k_1}w}}{{{\mathit{\Omega }_0}R}},\bar q = \frac{{{k_2}q}}{{{\mathit{\Omega }_0}}},\tau = {k_4}{\mathit{\Omega }_0}t\\ \mathit{\bar \Omega } = \frac{\mathit{\Omega }}{{{\mathit{\Omega }_0}}},\bar h = \frac{{{k_3}h}}{R},\bar x = \frac{{{k_3}x}}{R} \end{array} $ | (20) |
式中:Ω0为直升机模式下标准旋翼转速。长度、质量、升力系数、气动力和气动力矩的量纲一缩放如下
| $ \begin{array}{l} \bar l = \frac{{{k_1}}}{{{k_2}}}\frac{l}{R},{m_0} = \frac{{{k_4}}}{{{k_1}}}\frac{m}{{\rho {\rm{ \mathsf{ π} }}{R_3}}},{C_N} = \frac{2}{{{m_0}}}{C_T}\frac{{{k_1}}}{{{k_4}}}\\ {{\bar A}_z} = \frac{{{k_1}}}{{{k_4}}}\frac{{{A_z}}}{{m\mathit{\Omega }_0^2R}},{{\bar A}_x} = \frac{{{k_1}}}{{{k_4}}}\frac{{{A_x}}}{{m\mathit{\Omega }_0^2R}}\\ {{\bar M}_A} = \frac{{{k_2}}}{{{k_4}}}\frac{{{M_A}}}{{\mathit{\Omega }_0^2{I_{yy}}}} \end{array} $ | (21) |
为了使量纲一缩放后的状态变量和控制变量大小接近1,取k1=k2=100, k3=1, k4=0.01,则量纲一缩放后增广飞行动力学的主控方程可以表示为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}\mathit{\boldsymbol{\bar x}}}}{{{\rm{d}}\tau }} = f\left( {\mathit{\boldsymbol{\bar x}},\mathit{\boldsymbol{\bar a}},\mathit{\boldsymbol{\bar u}},\tau } \right)\\ \mathit{\boldsymbol{\bar a}} - g\left( {\mathit{\boldsymbol{\bar x}}} \right) = {\bf{0}} \end{array} \right. $ | (22) |
本文采用直接转换法将连续的最优控制问题转换为离散的非线性规划问题,然后利用序列二次规划算法进行求解。
将时间的量纲一τ等分为N-1个时间段
| $ \left\{ \begin{array}{l} {\tau _0} = {\tau _1} < {t_2} \cdots < {\tau _k} \cdots < {\tau _N} = {\tau _f}\\ {\tau _k} = {\tau _{k - 1}} + \Delta \tau \;\;\;\;\;\;\;\;\;k = 2, \cdots ,N\\ \Delta \tau = \left( {{\tau _f} - {\tau _0}} \right)/\left( {N - 1} \right) \end{array} \right. $ | (23) |
根据时间节点把连续空间下的状态变量、代数变量和控制变量进行离散可得
| $ {{\mathit{\boldsymbol{\bar x}}}_k} = \mathit{\boldsymbol{\bar x}}\left( {{\tau _k}} \right),{{\mathit{\boldsymbol{\bar a}}}_k} = \mathit{\boldsymbol{\bar a}}\left( {{\tau _k}} \right),{{\mathit{\boldsymbol{\bar u}}}_k} = \mathit{\boldsymbol{\bar u}}\left( {{\tau _k}} \right) $ | (24) |
由量纲一缩放后的参数组成的目标函数经过离散可得到
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_u {J_b} = \phi \left( {{{\mathit{\boldsymbol{\bar x}}}_1},{\tau _1},{{\mathit{\boldsymbol{\bar x}}}_N},{\tau _N}} \right) + \frac{1}{2}\sum\limits_{k = 1}^{N - 1} {\frac{1}{{N - 1}}} \left[ {L\left( {{{\mathit{\boldsymbol{\bar x}}}_k},} \right.} \right.}\\ {\left. {\left. {{{\mathit{\boldsymbol{\bar u}}}_k},{\tau _k}} \right) + L\left( {{{\mathit{\boldsymbol{\bar x}}}_{k + 1}},{{\mathit{\boldsymbol{\bar u}}}_{k + 1}},{\tau _{k + 1}}} \right)} \right]} \end{array} $ | (25) |
采用梯形公式对主控方程(22)中的微分方程进行离散,得到如下缺陷等式约束方程
| $ \begin{array}{l} {\bf{0}} \le {{\mathit{\boldsymbol{\bar x}}}_{k + 1}} - {{\mathit{\boldsymbol{\bar x}}}_k} - \frac{1}{2}\Delta \tau \left( {f\left( {{{\mathit{\boldsymbol{\bar x}}}_k},{{\mathit{\boldsymbol{\bar a}}}_k},{{\mathit{\boldsymbol{\bar u}}}_k},{\tau _k}} \right) + f\left( {{{\mathit{\boldsymbol{\bar x}}}_{k + 1}},} \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {{{\mathit{\boldsymbol{\bar a}}}_{k + 1}},{{\mathit{\boldsymbol{\bar u}}}_{k + 1}},{\tau _{k + 1}}} \right)} \right) \le {\bf{0}} \end{array} $ | (26) |
将路径约束作用于每一个时间节点,并将初始和末端边界条件约束分别作用于第1个和第N个时间节点,从而完成对连续最优控制问题的离散。应用稀疏序列二次规划算法[15]求解该非线性规划问题,然后对最优解中所有节点处的状态变量和控制变量进行分段3次Hermi te插值,即可得到光滑的最优轨迹和操纵曲线。
3 单发失效后轨迹数值优化本文以XV-15倾转旋翼机为例,计算短距起飞单发失效后的最优安全着陆过程,并与采用基本纵向刚体飞行动力学模型的文献[4]的计算结果进行对比。最后进一步分析不同驾驶员感知延迟时间对最优轨迹和操纵策略的影响。
倾转旋翼机从起飞到发动机失效的过程如下:全机质量为5 897 kg,襟翼/副翼配置为40°/25°,短舱倾转角保持70°,以静止状态在城区机场上滑跑起飞,加速度保持0.2g,当速度达到20.6 m/s时离地。发生单发失效的初始状态为速度2 2.6 m/s,高度3 m,航迹角10°,加速度0.2g,单发失效后驾驶员在反应1 s之后开始操纵。
本文与文献[4]均采用直接转换法和序列二次规划算法解决轨迹优化问题,为了方便对比,目标函数和以下末端约束与路径约束与文献保持一致:
目标函数为
| $ \min {J_b} = {{\bar x}_N} + \frac{{\dot {\bar x}_N^2}}{{2 \cdot 0.2\bar g}} $ | (27) |
末端边界条件为
| $ \begin{array}{l} - {5^ \circ } \le {\theta _f} \le {10^ \circ },{60^ \circ } \le {i_{nf}} \le {95^ \circ }\\ 0 \le {{\dot x}_f} \le 30.48\;{\rm{m/s}},0 \le {h_f} \le 0\\ - 3.048\;{\rm{m/s}} \le {{\dot h}_f} \le 0\\ 1\;{\rm{s}} \le {t_f} \le 15\;{\rm{s}} \end{array} $ | (28) |
路径约束为
| $ \begin{array}{l} - {40^ \circ } \le \theta \le {40^ \circ },0 \le h \le 15\;{\rm{m}}\\ {\rm{0}}{\rm{.78}} \le \mathit{\bar \Omega } \le 1.1,0.003 \le {C_T} \le 0.02\\ - {12^ \circ } < {\beta _{1c}} < {12^ \circ },{0^ \circ } \le {i_n} \le {90^ \circ } \end{array} $ | (29) |
以上路径约束可保证倾转旋翼机在着陆过程中旋翼不会发生大范围失速,从而确保飞行安全[4]。
由于本文采用增广飞行动力学模型,除了文献中的优化变量和约束条件,还增加了其他优化变量和约束条件
| $ \left\{ \begin{array}{l} 0 \le {u_{{\rm{col}}}},{x_{{\rm{col}}}},{\delta _{{\rm{col}}}} \le 1\\ 0 \le {u_{{\rm{lon}}}},{x_{{\rm{lon}}}},{\delta _{{\rm{lon}}}} \le 1\\ 0 \le {u_{{\rm{in}}}},{x_{{\rm{in}}}},{\delta _{{\rm{in}}}} \le {\rm{ \mathsf{ π} }}/2\\ - 0.15/{\rm{s}} \le {{\dot \delta }_{{\rm{col}}}} \le 0.15/{\rm{s}}\\ - 0.2/{\rm{s}} \le {{\dot \delta }_{{\rm{lon}}}} \le 0.2/{\rm{s}}\\ - 0.131\;{\rm{rad/s}} \le {{\dot \delta }_{{\rm{in}}}} \le 0.131\;{\rm{rad/s}} \end{array} \right. $ | (30) |
式(7)中的驾驶员神经肌肉滞后时间常数Tp一般取0.1 s,而感知延迟时间τp则根据驾驶员的知识经验和心理状态以及飞行任务而确定,一般为0.1~0.25 s[11, 16]。本文分别计算3种情况下的最优着陆轨迹和操纵策略:(1)不考虑驾驶员反应特性,即在轨迹优化计算中忽略式(9)和(10);(2)考虑驾驶员反应特性,感知延迟时间τp=0.1 s;(3)考虑驾驶员反应特性,感知延迟时间τp=0.25 s。
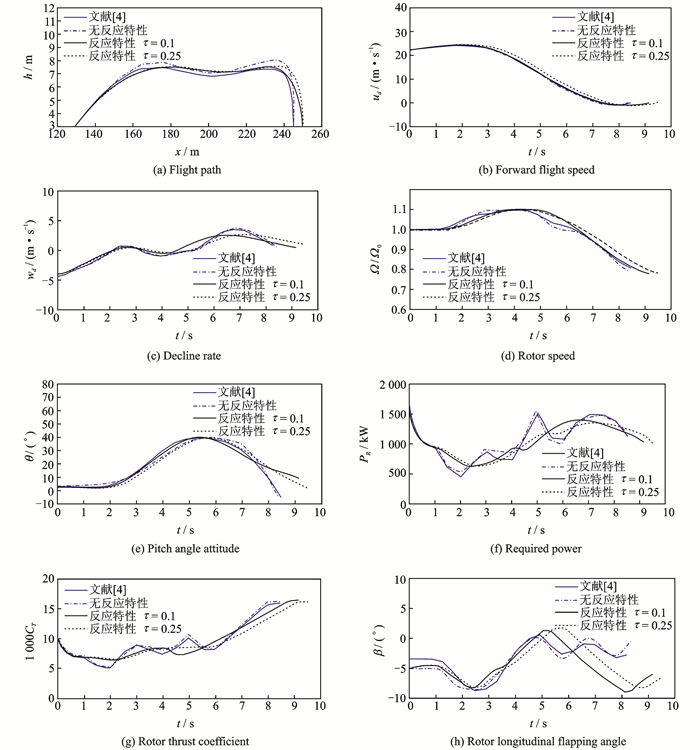
图 2所示为本文计算结果和文献[4]结果的对比。可以看出,不考虑驾驶员反应特性时,本文计算结果与文献的最优解吻合良好,说明本文建立的飞行动力学模型和采用的轨迹优化方法是可行的,但需用功率、拉力系数和旋翼后倒角都出现了比较剧烈的波动现象(图 2 (f)—(h));考虑驾驶员反应特性后,这些变量的时间历程更加柔和,且着陆时间和距离有所延长。这是因为本文所建模型可以模拟驾驶员的感知延迟、肌肉神经系统特性和操纵速率约束,不仅考虑到了驾驶员的感知延迟时间,还能避免在轨迹数值优化中可能会出现的操纵量高频振荡现象,从而使飞行状态量变化更加合理。除此之外,从图中可以看出,随着感知延迟时间τp的增加,着陆过程所需时间会延长,且着陆时垂向触地速度也会增大。因此经验丰富、反应较快的驾驶员可以更好的完成着陆,使垂向触地速度达到最小。
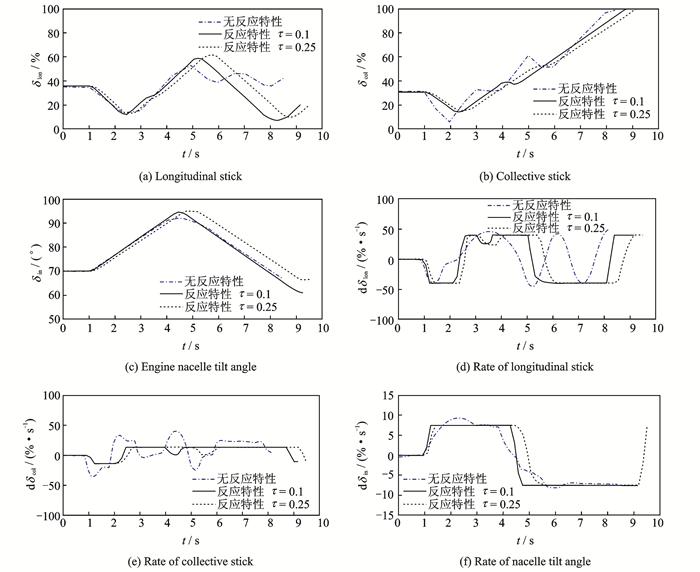
本文建立的增广飞行动力学模型包含了驾驶员操纵杆量,因此可以得到最优操纵量的时间历程,给驾驶员更多参考信息。如图 3所示,不考虑驾驶员反应特性时,优化得到的驾驶员纵向周期变距、总距操纵杆量以及操纵速率都出现了比较剧烈的波动现象;而考虑驾驶员反应特性后,驾驶员操纵量和操纵速率中的高频振荡现象均有所缓解,且飞行轨迹、速度和姿态角变化与文献基本一致,说明其最优操纵策略更加合理可行。除此之外,随着驾驶员感知时间的增加,着陆过程所需的操纵时间有所延长,但其操纵量变化趋势基本一致。
|
图 3 最优操纵量和操纵速率 Figure 3 Optimal controls and control rates |
以上结果可以说明本文建立的增广飞行动力学模型可以较好地模拟驾驶员的感知延迟、肌肉神经系统特性和操纵速率约束。
4 结论本文建立了可以模拟驾驶员反应特性的增广飞行动力学模型,并以XV-15倾转旋翼机为例,计算了短距起飞单发失效后的最优着陆过程,最后分析了不同驾驶员感知延迟时间对最优轨迹和操纵策略的影响。通过与相关文献结果的对比可以得到以下结论:
(1) 本文建立的增广飞行动力学模型较为准确,不仅适于倾转旋翼机单发失效后的轨迹数值优化,还可以考虑到驾驶员反应特性对最优轨迹和操纵策略的影响。
(2) 不考虑驾驶员反应特性时,本文的优化结果与采用基本纵向刚体飞行动力学模型的文献[4]的计算结果吻合良好,并且还包含了更多的操纵量信息,说明本文建立的模型和采用的轨迹优化方法是可行的。但需用功率、拉力系数、旋翼后倒角和一些操纵信息的时间历程均出现了比较剧烈的波动现象,会增加驾驶员的操纵负荷。
(3) 考虑驾驶员的反应特性后,优化得到的状态量、需用功率、拉力系数和旋翼后倒角变化更加柔和,飞行时间和着陆距离有所延长,操纵量变化更加合理,更符合驾驶员的实际操纵行为。这是因为本文所建模型可以模拟驾驶员感知延迟、肌肉神经系统特性和操纵速率约束,不仅考虑到了驾驶员的感知延迟时间,还能避免在轨迹数值优化中控制量可能会出现的操纵量高频振荡现象。
(4) 随着驾驶员的感知延迟时间增加,最优着陆过程所需时间会增加,且着陆时垂向触地速度也会增大,但操纵量变化趋势基本一致。说明经验丰富、反应较快的驾驶员可以更好地完成着陆,使垂向触地速度达到最小。本文建立的增广飞行动力学模型较好地模拟了驾驶员的反应特性,可以为驾驶员实施安全着陆提供依据。
| [1] |
CERBE T, REICHERT G, SCHRAGE D P. Short takeoff optimization for the XV-15 tiltrotor aircraft[C]//Proceedings of the 17th European Rotorcraft Forum. Paris, France: ERF International, 1991: 213-232. |
| [2] |
OKUNO Y, KAWACHI K.
Optimal takeoff procedures for a transport category tiltrotor[J]. Journal of Aircraft, 1993, 30(3): 291–292.
DOI:10.2514/3.46332
|
| [3] |
CARLSON E B. Optimal tiltrotor aircraft operations during power failure[D]. Minnesota: University of Minnesota, 1999. |
| [4] |
CARLSON E B, ZHAO Y J.
Optimal short takeoff of tiltrotor aircraft in one engine failure[J]. Journal of Aircraft, 2002, 39(2): 280–289.
DOI:10.2514/2.2925
|
| [5] |
CARLSON E B, ZHAO Y J.
Prediction of tilt-rotor height-velocity diagrams using optimal control theory[J]. Journal of Aircraft, 2003, 40(5): 896–905.
DOI:10.2514/2.6865
|
| [6] |
CARLSON E B, ZHAO Y J.
Optimal city-center takeoff operation of tiltrotor aircraft in one engine failure[J]. Journal of Aerospace Engineering, 2004, 17(1): 26–39.
DOI:10.1061/(ASCE)0893-1321(2004)17:1(26)
|
| [7] |
JHEMI A A, CARLSON E B, ZHAO Y J, et al.
Optimization of rotorcraft flight following engine failure[J]. Journal of the American Helicopter Society, 2004, 49(2): 117–126.
DOI:10.4050/JAHS.49.117
|
| [8] |
BOTTASSO C L, CROCE A, LEONELLO D, et al.
Optimization of critical trajectories for rotorcraft vehicles[J]. Journal of the American Helicopter Society, 2005, 50(2): 165–177.
DOI:10.4050/1.3092853
|
| [9] |
FERGUSON S W. A mathematical model for real time flight simulation of a generic tilt rotor aircraft: NASA CR-166536[R]. Washington: NASA, 1988: 192-442. |
| [10] |
JOHNSON W.
Helicopter theory[M]. New York: Dover Publications, INC, 1994: 179-184.
|
| [11] |
CAMERON N, THOMSON D G, MURRAY-SMITH D J.
Pilot modelling and inverse simulation for initial handling qualities assessment[J]. Aeronautical Journal, 2003, 107(1074): 511–520.
|
| [12] |
MCRUER D T, JEX H R.
A review of quasi-linear pilot models[J]. IEEE Transactions on Human Factors in Electronics, 1967(3): 231–249.
|
| [13] |
FERGUSON S W. Development and validation of a simulation for a generic tilt-rotor aircraft: NASA CR-166537[R]. Washington: NASA, 1989: 94-146. |
| [14] |
KIM S. Certification of transport category rotorcraft: 29-2C[S]. Washington: Federal Aviation Administration, Department of Transportation, 2014: 57-146. |
| [15] |
GILL P E, MURRAY W, SAUNDERS M A. User's guide for SNOPT version 7: Software for large-scale nonlinear programming[D]. California: University of California, 2006: 7-29. |
| [16] |
PAUSDER H J, JORDAN D.
Handling qualities evaluation of helicopters with different stability and control characteristics[J]. Vertica, 1976, 1(2): 125–134.
|
 2018, Vol. 50
2018, Vol. 50