飞机自动飞行中,驾驶员的指令信号转化为机械位移来偏转操纵舵面[1]。舵机及舵面系统作为飞行控制系统的执行机构,决定着飞机的动态响应品质[2]。在理想飞行动力学模型中,常常忽略舵面偏转速率的影响,模型的输出为理想化响应。但在真实情况下,作动器偏转速率对飞机响应及飞行品质影响显著。
升降舵作为主要的纵向飞行操纵面,在配平、操纵及增稳飞行中都有重要作用,且操纵性受舵面偏转速率影响显著。在机动飞行时,要求飞机响应快速且准确,如果舵面速率不满足要求,将会降低飞机的响应速度及飞行品质,影响飞行任务的完成,甚至危及飞行安全。
当前,在国内的飞机设计过程中,特别是在中小型通用飞机的设计中,对于舵面速率及功率指标,设计安全裕度一般很大,且实际需用速率指标和功率指标较为模糊,飞行品质难以定量分析。随着飞机飞行品质要求的提高、速度和载重的增加以及军用飞机的特殊要求,过大的舵面偏转速率及安全裕度不仅增加了作动器设计难度,而且对于材料和资源也是一种浪费。相反,过低的舵面偏转速率则容易导致舵面速率饱和,从而引发PIO(Pilot induced oscillation)振荡[3]。
本文提出一种方法,根据不同工况计算出需用的舵偏速率(带载荷的平均速率),并据此反算全状态最大空载速率,结合铰链力矩,计算舵偏范围内作动器功率最大值(即需用功率)并将其作为作动器功率设计值。该计算方法可为工程上设计升降舵作动器提供参考依据。
1 工况准则与平均速率计算方法在不同工况下,飞机的特性与响应均有不同,评价准则也不同。
1.1 工况分类在本次计算中,飞机共有巡航、巡逻、起飞和降落4种构型。飞行过程中的典型飞行工况如下。
(1) 精确机动操纵工况
起飞、降落等构型属于精确机动操纵工况。飞行员施加阶跃操纵输入,使飞机产生5%~10%的小幅度稳态过载增量。
(2) 大机动操纵工况
飞行员施加阶跃操纵输入,使飞机产生该状态30%的极限过载能增量。
(3) 极限机动操纵工况
极限机动操纵工况定义为:飞行员施加最大的阶跃操纵输入,使飞机产生该飞行状态下的极限稳态过载,对应升降舵的满舵状态。
由于涉及极限过载,飞行员操纵飞机达到过载的最大限制值。飞机在高速状态时,极限过载主要取决于使用过载限制值;在低速状态时,迎角较大,极限过载能力受迎角大小限制,根据状态点的速度和迎角,取使用过载和迎角限制过载较小值,作为极限稳态过载,如图 1所示。
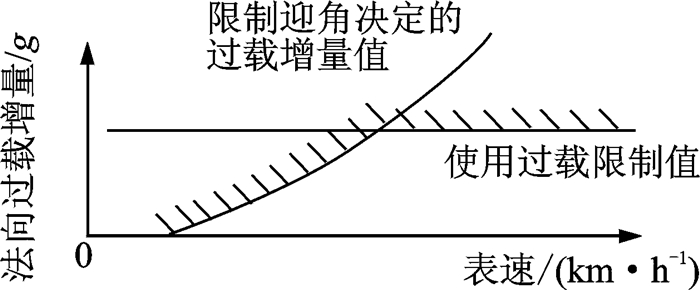
|
图 1 过载限制示意图 Figure 1 Overload limitation diagram |
1.2 飞行品质评价准则
在飞机的纵向短周期飞行品质中,与响应快速性相关性强的准则包括如下。
(1) 操纵期望参数(Control anticipation parameter,CAP)准则
纵向阶跃操纵时,用初始角加速度与稳态过载增量之比衡量飞行员对操纵效果推测(期望)的准确程度,定义为
| $ {\rm{CAP}} = \frac{{\Delta \ddot \theta \left( 0 \right)}}{{\Delta {n_y}\left( \infty \right)}} = \frac{{\omega _{n,sp}^2}}{{\frac{{\partial {n_y}}}{{\partial \alpha }}}} = \frac{{\omega _{n,sp}^2}}{{\left( {{V_ * }/g} \right)\left( {1/{t_d}} \right)}} $ | (1) |
式中:
(2) 俯仰角速率准则
俯仰角速率斜率最大点切线与x轴的交点,定义为有效延迟时间,表征飞机俯仰角速率初始响应的快速性。有效延迟时间t1的要求如表 1所示。
| 表 1 俯仰角速率准则对有效延迟时间的要求 Table 1 Requirement of pitch rate criterion to effective delay time |
(3) 时域准则
对阶跃操纵输入,法向过载的调节时间应满足Ts≤4 s。
升降舵速率设计应使得飞机响应满足以上3种准则要求。
1.3 带载荷平均舵面速率计算方法(1) 构造理想飞机传递函数,根据工况要求的稳态过载值,输入阶跃指令,生成期望的理想动态过载曲线;
(2) 由自然飞机从纵向操纵杆位移De到法向过载Ny的传递函数,求反函数,输出需用的舵面偏转响应;
(3) 将需用的舵面偏转输入速率限幅作动器,输出带有速率限制的舵偏;
(4) 将舵偏输入自然飞机,根据输出量评价飞行品质,得到需用舵偏速率。
2 铰链力矩特性分析分析舵面需用速率之后,结合舵面负载可确定舵面需用功率,舵面负载即为铰链力矩,是作用在舵面上的气动力相对于舵面铰链轴的力矩,升降舵的铰链力矩特性会对飞机的纵向操稳特性产生重大影响[4],其数值取决于舵面类型、几何形状、马赫数、迎角、侧滑角及舵面偏转等。一般来说,铰链力矩随迎角的增大在一定范围内基本呈线性变化,随舵面偏角的增大而增大[5]。执行机构(即舵面)的位移和力(矩)的分配使飞行员对操纵杆施加一定的力,舵面载荷直接影响操纵力的大小[6]。
目前采用风洞试验的手段来测定铰链力矩特性数据,在工程上是被大多数的气动设计师所接受,并认为是一种比较可靠的方法[7]。但目前在铰链力矩试验数据的雷诺数修正方法上,还缺少比较可靠的手段[8]。铰链力矩的表达式可近似写为
| $ {M_h} = {C_h} \cdot q \cdot S \cdot l $ | (2) |
式中:Ch为铰链力矩系数,q为速压,S为铰链线后面积,l为铰链线后平均气动弦长。铰链线后气动弦长和面积为定值,速压随马赫数的增大而增大。铰链力矩系数主要包括零升力矩系数、迎角力矩系数和舵偏力矩系数3部分,表达式近似如下[9]
| $ {C_h} = {C_{h0}} + {C_{h\alpha }} \cdot \alpha + {C_{h{\delta _e}}} \cdot {\delta _e} $ | (3) |
式中:Ch为铰链力矩系数;Ch0为零升力矩系数;Chα迎角力矩系数;Chδe为舵偏力矩系数;α为迎角;δe为升降舵舵偏。
其中,以舵面偏转产生的铰链力矩为主。铰链力矩不同与一般负载,其值大小随飞行状态改变,动压越大,铰链力矩越大[10]。
上述作动器需用速率分析中,所得结果为舵面平均需用速率,根据加入速率限制的舵机模型输出结果,其舵偏速率输出为定值,直至达到舵面偏转极限,因此计算功率时,使用平均需用功率最小值作为下边界。根据功率计算公式
| $ P = F \cdot v = {M_h} \cdot \omega $ | (4) |
式中:F为受力;v为线速度;Mh为铰链力矩;ω为舵面转轴角速度;
可知,计算各状态点的铰链力矩最大值,即可得驱动舵面的液压功率需求。
3 舵机需用功率计算由于铰链力矩是舵面的气动载荷,是气动力对铰链转轴的力矩,则根据功率计算公式
| $ P = F \cdot v = {F_{{\rm{air}}}} \cdot \omega \cdot d = {M_h} \cdot \omega $ | (5) |
舵面最小需求速率为精确机动工况中的平均速率,根据带载荷舵偏平均速率,利用积分求均值的原理,可反推空载舵面偏转速率,分析如下。
升降舵舵面偏转到极限位置时,偏转速率为最小;偏转到载荷最小时,偏转速率最大,因此,偏转速率是舵面位置的函数。
根据作动器流量与压力关系公式
| $ Q = {Q_0}\sqrt {1 - \frac{{\Delta P}}{{{P_0}}}} $ | (6) |
式中:Q为当前流量,Q0为空载流量,ΔP为活塞的压力差,P0为作动器进出口的压力差。
等号左右除以作动器活塞面积并乘以作动器行程到舵偏的系数,将压力差等效为铰链力矩,得到
| $ \omega = {\omega _0}\sqrt {1 - \frac{M}{{{k_M}{M_{\max }}}}} $ | (7) |
式中:ω为当前舵偏速率,ω0为空载流量,M为当前铰链力矩,Mmax为作动器所承受的最大铰链力矩,系数kM>1,kMMmax表征舵面最大承受的铰链力矩,一般情况,最大承受铰链力矩应不小于飞行包线中的最大铰链力矩的1.25倍。
当前铰链力矩和舵偏近似呈线性关系,令M=M0+Chδeδe,M0为零偏铰链力矩,Chδe为铰链力矩对舵偏的梯度,δe为舵偏。代入式(7),并对舵偏进行积分,得
| $ \omega = {\omega _0}\sqrt {1 - \frac{M}{{{k_M}{M_{\max }}}}} = {\omega _0}{\left[ {1 - \frac{{{M_0} + {C_{{h_{{\delta _e}}}}}{\delta _e}}}{{{k_M}{M_{\max }}}}} \right]^{\frac{1}{2}}} $ |
| $ \bar \omega = \frac{{\int_{{\delta _0}}^{{\delta _{\max }}} {\omega \left( {{\delta _e}} \right){\rm{d}}{\delta _e}} }}{{{\delta _{\max }} - {\delta _0}}} = \frac{{\int_{{\delta _0}}^{{\delta _{\max }}} {{\omega _0}{{\left[ {1 - \frac{{{M_0} + {C_{{h_{{\delta _e}}}}}{\delta _e}}}{{{k_M}{M_{\max }}}}} \right]}^{\frac{1}{2}}}{\rm{d}}{\delta _e}} }}{{{\delta _{\max }} - {\delta _0}}} $ |
式中:M0+Chδeδe为任意舵偏位置时的铰链力矩,δ0为该状态点的配平舵偏角。此处取kM=1.25。从公式中可以看出,随舵面载荷的增大,舵偏速率减小;舵面无载荷时,速率为ω0。
因为
| $ \begin{array}{*{20}{c}} {\int_{{\delta _0}}^{{\delta _{\max }}} {{\omega _0}\sqrt {1 - \frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} {\rm{d}}\delta } = }\\ {{\omega _0}\int_{{\delta _0}}^{{\delta _{\max }}} {{{\left( {1 - \frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} \right)}^{\frac{1}{2}}}{\rm{d}}\delta } = }\\ {{\omega _0}\frac{{{M_{\max }}}}{{{C_e}}}\int_{{\delta _0}}^{{\delta _{\max }}} {{{\left( {1 - \frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} \right)}^{\frac{1}{2}}}{\rm{d}}\frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} = }\\ { - {\omega _0}\frac{{{M_{\max }}}}{{{C_e}}}\int_{{\delta _0}}^{{\delta _{\max }}} {{{\left( {1 - \frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} \right)}^{\frac{1}{2}}}{\rm{d}}\left( {1 - \frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} \right)} = }\\ { - {\omega _0}\frac{{{M_{\max }}}}{{{C_e}}}\frac{2}{3}{{\left( {1 - \frac{{{M_0} + {C_e}\delta }}{{{M_{\max }}}}} \right)}^{\frac{3}{2}}}\left| {_{\delta = {\delta _0}}^{{\delta _{\max }}}} \right.} \end{array} $ |
所以
| $ \bar \omega = \frac{{ - {\omega _0}\frac{2}{3}\frac{{{M_{\max }}}}{{{C_e}}}\left[ {{{\left( {1 - \frac{{{M_0} + {C_e}{\delta _{\max }}}}{{{M_{\max }}}}} \right)}^{\frac{3}{2}}} - {{\left( {1 - \frac{{{M_0} + {C_e}{\delta _0}}}{{{M_{\max }}}}} \right)}^{\frac{3}{2}}}} \right]}}{{{\delta _{\max }} - {\delta _0}}} $ |
若平均舵偏速率已知,则可得到空载舵偏速率为
| $ {\omega _0} = \frac{{ - \bar \omega \left( {{\delta _{\max }} - {\delta _0}} \right)}}{{\frac{2}{3}\frac{{{M_{\max }}}}{{{C_e}}}\left[ {{{\left( {1 - \frac{{{M_0} + {C_e}{\delta _{\max }}}}{{{M_{\max }}}}} \right)}^{\frac{3}{2}}} - {{\left( {1 - \frac{{{M_0} + {C_e}{\delta _0}}}{{{M_{\max }}}}} \right)}^{\frac{3}{2}}}} \right]}} $ |
计算得到ω0后,任意δe位置的速率ω(δe)可求得,根据功率计算公式
| $ P\left( {{\delta _e}} \right) = F \cdot v = {F_{{\rm{air}}}} \cdot \omega \cdot d = {M_h}\left( {{\delta _e}} \right) \cdot \omega \left( {{\delta _e}} \right) $ |
可知功率P(δe)为舵偏的函数,求得函数最大值,即为为作动器的最低功率需求。
4 仿真计算结果 4.1 舵面空载速率巡航、巡逻、起飞和降落4种构型的状态点循环计算,得到的ω0范围如表 2所示。
| 表 2 空载速率范围 Table 2 No-load surface rate range |
柱形图如图 2所示。飞机处于起飞和降落构型中,机动动作幅度限制较为严格,空载速率偏低,同时液压流量着重倾向于供应增升装置。
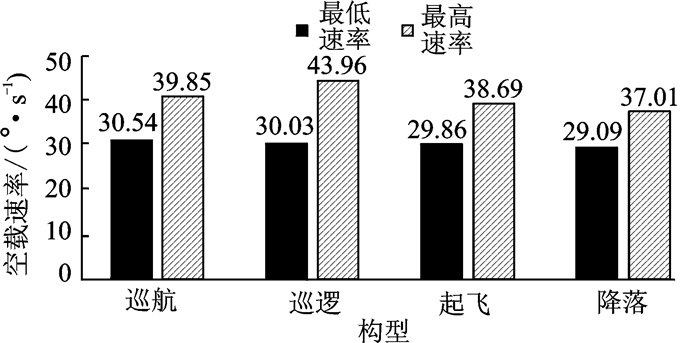
|
图 2 不同构型空载速率范围 Figure 2 No-load surface rate range of different configurations |
取得空载速率ω0最小值与最大值的状态点及详细参数如表 3所示。
| 表 3 空载速率最大最小值对应状态点 Table 3 State points that coresponds the maximum and minimum no-load surface rate |
空载速率计算结果与配平舵偏、极限舵偏、配平与最大铰链力矩等都有直接关系,上面所列结果为了说明空载速率的极限及边界范围,状态点的构型、高度及速度仅代表空载速率最大或最小时的状态,由计算结果决定。
根据结果的取值范围,最终确定ω0=43.957 3 °/s,取全包线最大值。
4.2 作动器铰链力矩及需用功率结果将部分计算结果与某两型支线客机对比如表 4所示。
| 表 4 参数对比 Table 4 Parameters comparison |
根据表 4数据,涡桨飞机的空载偏转速率大于两型支线客机,又由于受到涡桨发动机滑流影响,铰链力矩偏大,结果可信度较高;单块舵面最大铰链力矩介于其他两个型号之间,该最大力矩在巡逻状态点右舵面,0.45Ma飞行速度,拉力系数为0.02时取得。
计算作动器需用功率时,利用该点的力矩值与实际的偏转速率相乘,每个状态点循环计算后,取该状态点内所有舵偏位置功率的最大值。全包线内最大功率为
| $ {P_{\max }} = 1\;690.6\;{\rm{W}} $ |
(1) 舵机功率需满足全包线全位置的液压驱动能力,故最小需用速率应取各个状态点及所有舵面位置的需用功率最大值作为阈值,即需用液压功率为1 690.6 W,单块最大铰链力矩在右舵面取得,此时拉力系数为0.02,飞行速度为0.45Ma。
(2) 在单个状态点范围内对比,巡航巡逻构型中,铰链力矩及需用功率随拉力系数的增加而增加,即增大发动机动力,舵面负载也增大;正常平飞时随速度的增加,需用拉力系数减小,计算时需采用插值法确定拉力系数值。
(3) 由平均需用功率反算得到舵面空载速率,进而获取各状态点所有舵面位置的偏转速率,结合各舵偏位置的铰链力矩,计算得到需用功率;舵机在偏转时,力矩最小时速率最大。
实际上,作动器提供的铰链力矩为平衡当前铰链力矩和提供舵偏角加速度的力矩之和,为保证功率满足要求,同时考虑液压系统的尺寸参数设计标准,实际设计时的功率数值应大于计算结果,以保障舵面能够顺利克服负载转动,并具备应对极端载荷冲击的能力。本文提出的功率计算方法对作动器工程设计具有一定的参考价值和应用意义。
| [1] |
方振平.
带自动器飞机飞行动力学[M]. 北京: 国防工业出版社, 2010: 29.
FANG Zhenping. Aircraft flight dynamics with automata[M]. Beijing: National Defence Industry Press, 2010: 29. |
| [2] |
何倩琳, 王立新.
飞翼布局飞机舵面偏转速率设计[J]. 北京航空航天大学学报, 2015, 41(9): 1729–1735.
HE Qianlin, WANG Lixin. Design of rudder deflection rate of flying wing layout aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1729–1735. |
| [3] |
刘瑜, 王海维, 贾晓鹏.
升降舵速率饱和引发的纵向PIO趋势预测方法[J]. 飞行力学, 2014, 32(2): 174–178.
LIU Yu, WANG Haiwei, JIA Xiaopeng. Longitudinal PIO trend prediction method caused by elevator rate saturation[J]. Journal of Flight Mechanics, 2014, 32(2): 174–178. |
| [4] |
乔伟, 王洪伟.运12F飞机升降舵铰链力矩补偿方案分析[C]//中国航空学会青年科技论坛.北京: 航空工业出版社, 2012.
QIAO Wei, WANG Hongwei. Analysis of the compensation method for the hinge torque of the 12F aircraft elevator[C]//China Aviation Society Youth Science and Technology Forum. Beijing: Aviation Industry Press, 2012. |
| [5] |
黄宗波.舵面铰链力矩低速特性研究[D].绵阳: 中国空气动力研究与发展中心, 2007.
HUANG Zongbo. Research on low speed characteristics of rudder hinge moment[D]. Mianyang: China Aerodynamics Research and Development Center, 2007. |
| [6] |
李为吉.
飞机总体设计[M]. 陕西: 西北工业大学出版社, 2009: 141.
LI Weiji. Overall design of aircraft[M]. Shaanxi: Northwestern Polytechnical University Press, 2009: 141. |
| [7] |
杨康智, 陈春鹏.
某型飞机升降舵铰链力矩头部补偿研究[J]. 军民两用技术与产品, 2014(7): 13–14.
DOI:10.3969/j.issn.1009-8119.2014.07.010 YANG Kangzhi, CHEN Chunpeng. Research on head torque compensation of a certain aircraft elevator[J]. Dual-use Technology and Products, 2014(7): 13–14. DOI:10.3969/j.issn.1009-8119.2014.07.010 |
| [8] |
王百争.飞机铰链力矩风洞试验数据修正方法研究[C]//近代实验空气动力学会议.哈尔滨: 原子能出版社, 2009.
WANG Baizheng. Research on correction method of aircraft hinge torque wind tunnel test data[C]//Modern Experimental Aerodynamics Conference. Harbin: Atomic Enengy Press, 2009. |
| [9] |
方振平, 陈万春, 张曙光.
航空飞行器飞行动力学[M]. 北京: 北京航空航天大学出版社, 2010: 227.
FANG Zhenping, CHEN Wanchun, ZHANG Shuguang. Flight dynamics of aerospace vehicles[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010: 227. |
| [10] |
吴森堂, 费玉华.
飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2009: 169.
WU Sentang, FEI Yuhua. Flight control system[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2009: 169. |
 2018, Vol. 50
2018, Vol. 50


