飞行包线综合反映了飞机的气动、推力、飞控和结构等因素对各类飞行参数的限制。除最常见的飞行高度-速度包线外,近年来,有学者提出了反映民机飞行失控状态的5种包线,涵盖了飞机姿态角约束、空速-过载约束以及姿态角-操纵杆量约束等[1]。飞行包线保护是飞行控制系统的重要任务之一,保护控制律往往作为内环控制律,除对上述飞行参数进行保护以外,设计过程中还应考虑执行器饱和、响应速度限制等各类控制边界。
民机飞控系统一般基于分段小扰动线性模型设计线性控制律,采用传统增益调度方法获得变化的控制增益[2]。基于小扰动模型设计的飞行边界保护算法往往难以应对一些特情飞行条件。以大气扰动环境下的飞行为例,在扰动风作用下,飞机瞬时偏离平衡状态,在小扰动模型基础上设计的控制律无法实现有效的边界保护。应对这一问题,有学者提出了在保持横侧稳定的前提下,进行空速最大减速度约束[3]、俯仰变化率约束[4]等边界保护策略。此外,上述问题也凸显出采用小扰动模型研究飞行边界保护的方法存在不足。值得一提的是,近年来针对简化非线性模型的非线性控制律设计研究,往往缺少对简化模型的逼真度或有效性的验证。
近年来,以现代增益调度、反馈线性化为设计目标,出现了线性参数变化(Linear parameter varying,LPV)模型。L PV模型具有线性模型的特点,其系数矩阵是关于一组调度变量的函数。调度变量可根据系统的可测量来定义,使用中通过切换算法不断更新系数矩阵[5]。对全量非线性模型进行合理降阶,并针对性地选取调度变量,构建LPV飞行动力学模型,从而可对具体飞控任务进一步设计控制律。
边界保护控制算法通常是根据当前状态和约束要求,反求控制输入。国外有学者曾提出动态配平、峰值响应估计和非线性响应函数等设计方法。其中,动态配平法是在飞行边界状态稳定的前提下, 采用有约束优化方法求解操纵输入[6]。峰值响应估计法是在前者基础上,假定达到包线边界的控制输入为阶跃信号[7]。两种方法都基于线性模型,且求解结果均偏于保守。非线性响应函数法则采用神经网络描述从观测状态到输入的非线性映射关系,实现输入范围的动态估计[8], 但神经网络等非机理模型往往难以模拟飞机真实动态。
本文拟研究一种基于LPV模型的模型参考自适应边界保护控制方法,通过LPV模型随调度变量的动态变化,尽可能减小与高逼真度全量模型的失配;引入广义预测控制自适应算法,研究用于边界保护的前馈和反馈自适应控制律。本文拟对LPV模型的逼真度、自适应预测控制算法及其对飞行状态的约束乃至飞行边界保护能力进行全面的仿真验证研究。
1 LPV模型参考自适应控制 1.1 民机LPV动力学建模首先研究一种能够精确反映飞行动力学响应的LPV模型。LPV建模主要有雅克比线化、状态转移和函数替换等3种方法。雅克比法是取全量模型在某一平衡点处的一阶近似;状态转移法则通过偏微分计算,将非调度变量和控制输入表示为调度变量的连续可微函数。这两种方法均需构建调度变量的平衡点图,通过平衡点间的插值实现状态更新。模型精度与选取的平衡点数量有关,且只能保证偏离平衡点的小范围内有效,不具有超出平衡点图的外插能力[5, 9]。函数替换法则基于单个平衡点,将非线性系统表达为仿射参数依赖模型加分解函数的模型结构,分解函数通过优化计算求解。研究表明,函数替换LPV模型具有外插能力,能够比前两种模型更好地模拟系统动态[5, 10]。本文采用函数替换LPV建模方法,以纵向飞行动力学建模为例,采用下述状态空间模型表示
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot z}}}\\ {\mathit{\boldsymbol{\dot w}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( \mathit{\boldsymbol{z}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( \mathit{\boldsymbol{z}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{z}}\\ \mathit{\boldsymbol{w}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]\mathit{\boldsymbol{u}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_1}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{k}}_2}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]} \end{array} $ | (1) |
式中:z(t)∈Rnz为调度状态,w(t)∈Rnw为非调度状态,u(t)∈Rnu为控制输入。纵向动力学模型中,选取影响飞机气动特性的主要参数[V, α, h]T为调度变量;选取[q, θ]T为非调度变量;控制输入[δe, σ, T]T,分别为升降舵偏角、水平安定面偏角和发动机推力。调度变量、非调度变量及控制输入为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\eta }}_z} = \mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}\\ {\mathit{\boldsymbol{\eta }}_w} = \mathit{\boldsymbol{w}} - {\mathit{\boldsymbol{w}}_{{\rm{trim}}}}\\ {\mathit{\boldsymbol{\eta }}_u} = \mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{u}}_{{\rm{trim}}}} \end{array} \right. $ | (2) |
式中:下标trim为对应的平衡飞行状态,即选取(ztrim, wtrim, utrim)为常值参考点。将式(2)代入式(1)中,有
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot \eta }}}_z}}\\ {{{\mathit{\boldsymbol{\dot \eta }}}_w}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_z}}\\ {{\mathit{\boldsymbol{\eta }}_w}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]{\mathit{\boldsymbol{\eta }}_u} + \mathit{\boldsymbol{F}}} \end{array} $ | (3) |
式中, F是关于(ηz, ztrim, wtrim, utrim)的分解函数,其展开表达式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}}}\\ {{\mathit{\boldsymbol{w}}_{{\rm{trim}}}}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]{\mathit{\boldsymbol{u}}_{{\rm{trim}}}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{k}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]} \end{array} $ | (4) |
函数替换方法的关键在于重新构造函数F,将其描述为参数时变形式
| $ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{f}}\left( z \right){\mathit{\boldsymbol{\eta }}_z} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_1}\left( z \right)}\\ {{\mathit{\boldsymbol{f}}_2}\left( z \right)} \end{array}} \right]{\mathit{\boldsymbol{\eta }}_z} $ | (5) |
将式(5)代入式(3)中,得
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot \eta }}}_z}}\\ {{{\mathit{\boldsymbol{\dot \eta }}}_w}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{f}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right){\mathit{\boldsymbol{A}}_{12}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{f}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right){\mathit{\boldsymbol{A}}_{22}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right] \times }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_z}}\\ {{\mathit{\boldsymbol{\eta }}_w}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]{\mathit{\boldsymbol{\eta }}_u}} \end{array} $ | (6) |
式(5)的系数矩阵有多种实现,可通过优化计算,合理选取系数矩阵,使其尽可能地逼近原非线性系统。对调度变量[V, α, h]T的选取划分为i×j×k的网格形式,可将求解F的问题转化为求解带绝对值约束的线性规划问题。在模型运行过程中,根据调度变量变化实现LPV模型系统矩阵和输入矩阵的动态更新,从而降低LPV模型与全量模型的失配,方便后续有效地设计边界保护控制律。
建立式(7)所示的性能指标,以量化LPV模型与全量非线性模型动态响应的差别,有
| $ J = \sum\limits_{i = 1}^{{n_x}} {\frac{1}{{{t_{\rm{f}}}}}\sum\limits_{t = 0}^{{t_{\rm{f}}}} {\frac{{{{\left[ {{x_{nl\left( i \right)}}\left( t \right) - {x_{{\rm{LPV}}\left( i \right)}}\left( t \right)} \right]}^2}}}{{{S_i}}}} } $ | (7) |
式中:xnl(i)和xLPV(i)分别为两种模型的对应状态,Si是每个状态的归一化系数,tf是计算时长。LPV模型参考自适应控制过程中,一旦J值过大,将重新优化计算式(5),生成新的LPV模型,从而降低模型失配对控制律带来的不利影响。
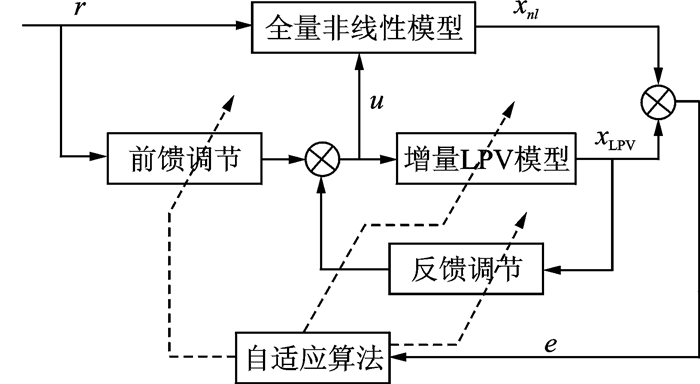
1.2 LPV模型参考自适应控制方案设计用于飞行边界保护控制的LPV模型参考自适应控制方案如图 1所示。
|
图 1 LPV模型参考自适应边界保护控制 Figure 1 Flight boundary protection based on LPV model reference adaptive con trol |
如图 1所示,以全量模型作为理想参考模型。全量模型可完整描述非线性飞行动力学特性,其输出能够反映飞机的真实输出。以LPV模型为控制对象,通过调度变量的动态变化来跟踪全量模型的变化。
通过自适应算法分别设计前馈和反馈调节器,进行飞行边界保护控制。边界约束包括状态约束、控制限幅及其控制增量约束等。前馈和反馈控制应具有实时性,能够快速响应边界约束的动态变化。此外,自适应机构应考察LPV模型与全量模型的失配程度,一旦超过失配阈值,则重新通过优化计算来更新LPV模型。
1.3 LPV模型自校正前馈和反馈控制器设计采用广义预测控制的自适应控制方法,首先将式(6)的增量L PV模型转为离散形式,有
| $ \left\{ \begin{array}{l} \Delta \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{B}}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right)\\ {\mathit{\boldsymbol{y}}_{\rm{c}}}\left( k \right) = {\mathit{\boldsymbol{C}}_{\rm{c}}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{y}}_{\rm{c}}}\left( {k - 1} \right)\\ {\mathit{\boldsymbol{y}}_{\rm{b}}}\left( k \right) = {\mathit{\boldsymbol{C}}_{\rm{b}}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{y}}_{\rm{b}}}\left( {k - 1} \right) \end{array} \right. $ | (8) |
式中:yc(k)和yb(k)分别为被控输出量和约束输出量,后者用于定义飞行边界状态约束。在每一采样时刻,控制限幅、增量约束和状态约束可表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{\min }}\left( k \right) \le \mathit{\boldsymbol{u}}\left( k \right) \le {\mathit{\boldsymbol{u}}_{\max }}\left( k \right)\\ \Delta {\mathit{\boldsymbol{u}}_{\min }}\left( k \right) \le \Delta \mathit{\boldsymbol{u}}\left( k \right) \le \Delta {\mathit{\boldsymbol{u}}_{\max }}\left( k \right)\\ {\mathit{\boldsymbol{y}}_{\min }}\left( k \right) \le {\mathit{\boldsymbol{y}}_{\rm{b}}}\left( k \right) \le {\mathit{\boldsymbol{y}}_{\max }}\left( k \right) \end{array} \right. $ | (9) |
为使LPV模型的响应输出跟随参考信号,构建以下形式的代价函数
| $ \begin{array}{*{20}{c}} {J\left( {\mathit{\boldsymbol{x}}\left( k \right),\Delta \mathit{\boldsymbol{u}}\left( k \right)} \right) = {{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right)} \right\|}^2} + }\\ {{{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_y}\left( {{\mathit{\boldsymbol{y}}_{p,c}}\left( {k + 1\left| k \right.} \right) - \mathit{\boldsymbol{r}}\left( {k + 1} \right)} \right)} \right\|}^2}} \end{array} $ | (10) |
式中:Γy和Γu分别是由预测时域p和控制时域m的维数所决定的权矩阵。yp, c(k+1|k)则是在k时刻预测k+1时刻的p步预测方程。通过状态方程递推可求得预测方程的解析形式,有
| $ {\mathit{\boldsymbol{y}}_{p,c}}\left( {k + 1\left| k \right.} \right) = {\mathit{\boldsymbol{S}}_x}\Delta \mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{y}}_{\rm{c}}}\left( k \right) + {\mathit{\boldsymbol{S}}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right) $ | (11) |
其各项系数的展开式有
| $ {\mathit{\boldsymbol{S}}_x} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{\rm{c}}}\mathit{\boldsymbol{A}}}\\ {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^2} + {\mathit{\boldsymbol{C}}_{\rm{c}}}\mathit{\boldsymbol{A}}}\\ \vdots \\ {\sum\limits_{i = 1}^p {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^i}} } \end{array}} \right]_{p \times 1}}\;\;\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{{n_{\rm{c}}} \times {n_{\rm{c}}}}}}\\ {{\mathit{\boldsymbol{I}}_{{n_{\rm{c}}} \times {n_{\rm{c}}}}}}\\ \vdots \\ {{\mathit{\boldsymbol{I}}_{{n_{\rm{c}}} \times {n_{\rm{c}}}}}} \end{array}} \right]_{p \times 1}} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{\rm{u}}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{B}}_{\rm{u}}}}&{}&{}&{}\\ {\sum\limits_{i = 1}^2 {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^{i - 1}}{\mathit{\boldsymbol{B}}_{\rm{u}}}} }&{{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{B}}_{\rm{u}}}}&{}&{}\\ \vdots&\vdots &{}&{}\\ {\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^{i - 1}}{\mathit{\boldsymbol{B}}_{\rm{u}}}} }&{\sum\limits_{i = 1}^{m - 1} {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^{i - 1}}{\mathit{\boldsymbol{B}}_{\rm{u}}}} }& \cdots &{{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{B}}_{\rm{u}}}}\\ \vdots&\vdots&\vdots&\vdots \\ {\sum\limits_{i = 1}^p {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^{i - 1}}{\mathit{\boldsymbol{B}}_{\rm{u}}}} }&{\sum\limits_{i = 1}^{p - 1} {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^{i - 1}}{\mathit{\boldsymbol{B}}_{\rm{u}}}} }& \cdots &{\sum\limits_{i = 1}^{p - m + 1} {{\mathit{\boldsymbol{C}}_{\rm{c}}}{\mathit{\boldsymbol{A}}^{i - 1}}{\mathit{\boldsymbol{B}}_{\rm{u}}}} } \end{array}} \right]}_{p \times m}}} \end{array} $ |
文献[11]给出了无约束广义预测控制的解析形式
| $ \Delta \mathit{\boldsymbol{u}}\left( k \right) = {\mathit{\boldsymbol{K}}_{{\rm{mpc}}}}\left( {\mathit{\boldsymbol{r}}\left( {k + 1} \right) - {\mathit{\boldsymbol{S}}_x}\Delta \mathit{\boldsymbol{x}}\left( k \right) - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{y}}_{\rm{c}}}\left( k \right)} \right) $ | (12) |
式中:r(k+1)为在预测时域内的参考输入,该项形成前馈调节项;yc(k)为由增量LPV模型确定的预测方程的反馈调节项。
1.4 飞行边界保护控制算法设计式(12)是引用广义预测控制方法进行的无约束条件下前馈和反馈控制器设计,其形式是解析的。在实时飞行边界保护中,须引入式(9)所示的控制约束。在有外部扰动下,状态约束可能随时变化。因此,必须研究一种满足动态约束变化的边界保护算法。
在有约束条件下,无法获得解析的控制律,本文拟采用二次规划(Quadratic programming, QP)进行数值计算。首先,将式(10)转为QP的目标函数形式。定义
| $ {\mathit{\boldsymbol{E}}_p}\left( {k + 1\left| k \right.} \right) = \mathit{\boldsymbol{r}}\left( {k + 1} \right) - {\mathit{\boldsymbol{S}}_x}\Delta \mathit{\boldsymbol{x}}\left( k \right) - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{y}}_{\rm{c}}}\left( k \right) $ | (13) |
则式(10)转为
| $ \begin{array}{*{20}{c}} {J = {{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_y}\left( {{\mathit{\boldsymbol{S}}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right) - {\mathit{\boldsymbol{E}}_p}\left( {k + 1\left| k \right.} \right)} \right)} \right\|}^2} + }\\ {{{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right)} \right\|}^2}} \end{array} $ | (14) |
将其展开后,由于‖ΓyEp(k+1|k)‖2项与Δu(k)无关,式(14)的优化问题等价于
| $ \begin{array}{*{20}{c}} {\tilde J = \Delta \mathit{\boldsymbol{u}}{{\left( k \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_{\rm{u}}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_y^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_y}{\mathit{\boldsymbol{S}}_{\rm{u}}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{u}}^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{u}}}} \right)\Delta \mathit{\boldsymbol{u}}\left( k \right) - }\\ {2\mathit{\boldsymbol{E}}_p^{\rm{T}}\left( {k + 1\left| k \right.} \right)\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_y^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_y}\mathit{\boldsymbol{E}}_p^{\rm{T}}\left( {k + 1\left| k \right.} \right)\Delta \mathit{\boldsymbol{u}}\left( k \right)} \end{array} $ | (15) |
其次,形成控制限幅约束和控制增量约束。由于QP问题的独立变量就是控制增量序列,因而可将控制增量约束直接写成Cz≥b的形式。类似地,通过控制增量累加也可将控制限幅约束表示成这种形式。
再次,对系统约束输出,可参考yp, c(k+1|k)推导类似的方法,推导出系统未来p步预测的约束输出方程
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{pb}}\left( {k + 1\left| k \right.} \right) = {\mathit{\boldsymbol{S}}_{xb}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{b}}}{\mathit{\boldsymbol{y}}_{\rm{b}}}\left( k \right) + }\\ {{\mathit{\boldsymbol{S}}_{ub}}\Delta \mathit{\boldsymbol{u}}\left( k \right)} \end{array} $ | (16) |
其展开式与式(11)类似。将式(16)代入式(9)规定的控制增量约束中,形成Cz≥b形式的输入约束为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{S}}_{ub}}}\\ {{\mathit{\boldsymbol{S}}_{ub}}} \end{array}} \right]\Delta \mathit{\boldsymbol{u}}\left( k \right) \ge }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{xb}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{b}}}{\mathit{\boldsymbol{y}}_{\rm{b}}}\left( k \right) - {\mathit{\boldsymbol{y}}_{\max }}\left( {k + 1} \right)}\\ { - {\mathit{\boldsymbol{S}}_{xb}}\Delta \mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{b}}}{\mathit{\boldsymbol{y}}_{\rm{b}}}\left( k \right) + {\mathit{\boldsymbol{y}}_{\min }}\left( {k + 1} \right)} \end{array}} \right]} \end{array} $ | (17) |
最后,综合式(15)性能指标、控制限幅和控制增量约束、状态输出约束式(17),形成约束预测控制的QP求解形式为
| $ \left\{ \begin{array}{l} \mathop {{\rm{Min}}}\limits_{\Delta \mathit{\boldsymbol{u}}\left( k \right)} \tilde J\\ {\mathit{\boldsymbol{C}}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right) \ge \mathit{\boldsymbol{b}}\left( {k + 1\left| k \right.} \right) \end{array} \right. $ | (18) |
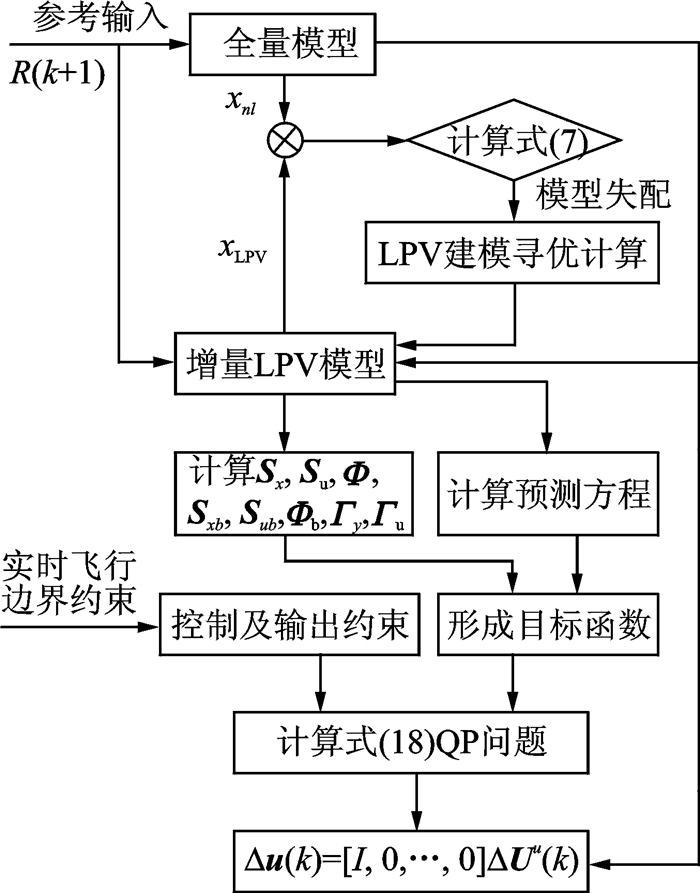
根据上述推导,基于LPV模型参考自适应飞行边界保护的算法流程如图 2所示。根据预测控制的滚动优化机理,在每个控制周期内,根据增量LPV模型计算预测方程并形成目标函数。根据实时飞行边界约束,形成控制及状态约束,从而通过QP数值求解有约束预测控制问题式(18)。将求解获得的最优解的第一列元素作为控制量,同时作为全量模型和增量LPV模型的控制输入。通过比较两者的响应,计算指标式(7),决定是否更新LPV模型。
|
图 2 飞行边界保护控制流程 Figure 2 Flow chart for flight boundary protection control |
上述算法流程提供了一种基于LPV参考模型,根据实时飞行边界求解有约束预测控制问题的数值方法,该算法可在控制周期内实时完成。算法流程中,通过计算(7)式考查LPV模型与全量模型是否失配。一旦出现失配,将通过线性规划重新构造F矩阵(即式(5)),从而形成新的LPV模型。在网格划分数不大时,这一优化过程可以在控制周期内完成。在成功获得新的F矩阵前,仍以前一个F矩阵代入计算。因此,可以保证LPV模型参考自适应控制算法的实时性。
2 LPV模型及自适应控制算法仿真本节拟通过仿真手段,先后考查LP V模型对全量模型的逼近能力、有约束广义预测控制算法性能及其对飞行边界的保护能力。基于B747-100飞机建模数据[12],建立该机全量纵向动力学模型和LPV模型。
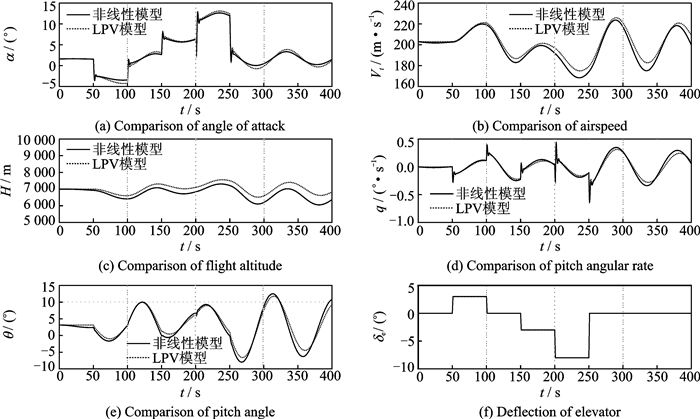
2.1 参考LPV模型动态性能测试将模型配平在7000m高度,以203m/s空速定直平飞。建立LPV模型,为优化求解式(5),选取网格划分为:迎角α∈[0, 5, 10],空速V∈[160, 200, 240],高度h∈[6 500, 7 000, 7 500]。图 3所示为LPV模型的动态性能测试。升降舵偏角δe按图 3(f)所示的测试激励偏转。
|
图 3 LPV模型与非线性模型的操纵响应对比 Figure 3 Comparison of control response between LPV model and nonlinear m odel |
从仿真结果可直观看出,LPV模型能较好地逼近全量模型的瞬时动态。特别是在大迎角状态时,动力学系统已处于气动包线边界,LPV模型仅靠外插仍能较好地逼近全量模型,体现出适应大范围动态变化的能力。除上述仿真结果以外,论文还进行了多组动态响应测试。通过多组试验数据的对比分析表明,LPV模型对全量模型具有较好的逼近能力。
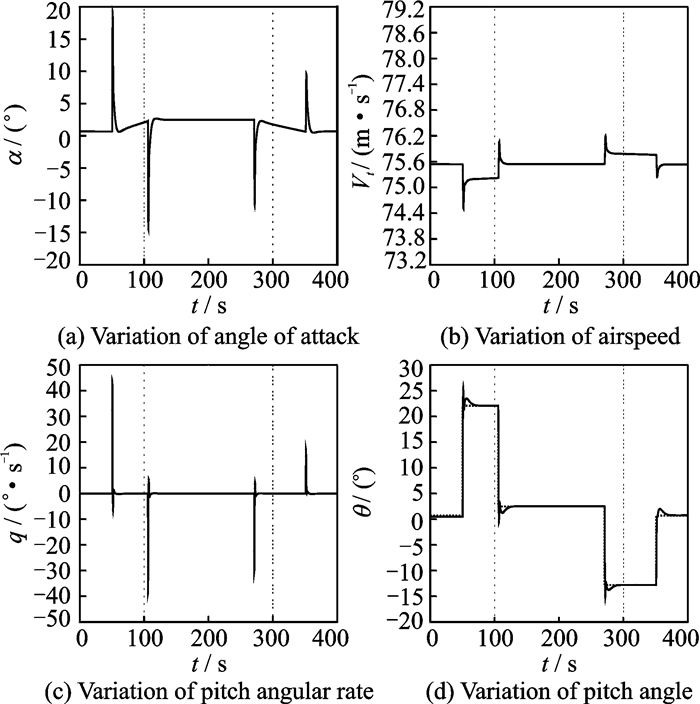
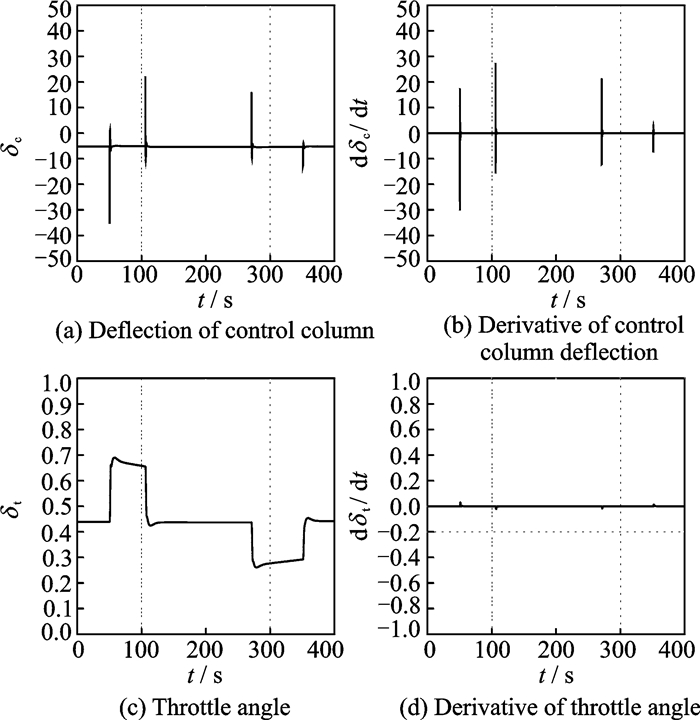
2.2 无约束广义预测控制仿真将飞机配平在低速飞行状态,以俯仰角θ为参考指令。整个模型参考自适应系统在接收到参考指令后,飞机俯仰角迅速跟踪到参考指令,但此时飞机已超过失速迎角,如图 4所示。图 5所示的升降舵偏角及其瞬时增量也远远超出执行器的实际能力。
|
图 4 无约束预测控制仿真 Figure 4 Simulation of unconstrained predictive control |
|
图 5 控制及其增量仿真 Figure 5 Simulation of controls and their increments |
2.3 飞行边界保护控制仿真
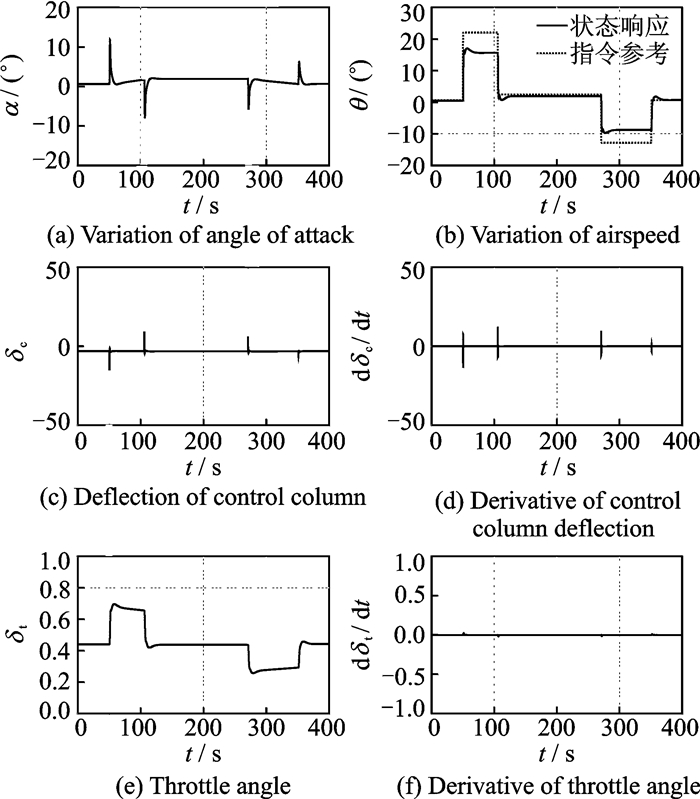
在2.2节仿真实验的基础上,根据B747-100飞机的操纵系统参数[12],引入飞行边界约束:-23°≤u1(k)≤17 °,-37°/s≤Δu1(k)≤37 °/s,-5°≤α(k) ≤17°。采用约束预测控制算法,获得仿真结果如图 6所示。可以看出,约束广义预测控制算法根据舵偏角和迎角约束,对俯仰角参考指令进行了合理的响应。θ保持在15 °左右,迎角、升降舵控制量及其瞬时增量均被保持在约束范围内。
|
图 6 飞行边界保护控制仿真 Figure 6 Simulation of flight boundary protection control |
3 结束语
合理的飞行边界保护可以有效地预防各类特情诱发的飞行失控。本文研究了一种基于LPV飞行动力学模型的模型参考自适应飞行边界保护控制方法。首先建立LPV模型,通过调度变量的动态变化尽可能减小与高逼真度全量模型的失配,从而提高控制对象的建模逼真度。其次,将飞行边界保护转为有约束广义预测控制问题。研究了一种考虑飞行状态约束、控制量及其增量约束的有约束广义预测控制算法,并通过二次规划进行数值求解。最终通过实时计算LP V模型与参考全量模型的失配进行模型更新,形成模型参考自适应控制机制;通过有约束广义预测控制形成LPV模型的前馈和反馈自适应调节机制。通过仿真分析表明, 本文建立的纵向LPV模型能够较好地逼近全量模型, 反映出瞬时飞行动态。在以LPV模型为模型参考的基础上,通过有约束广义预测控制数值算法能够有效地将飞行状态限制在约束范围内,从而为实现完整的飞行边界保护奠定基础。
| [1] |
WILBORN J, FOSTER J.Defining commercial trans-port loss-of-control: A quantitative approach[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Rhode Island, USA: AIAA, 2004: 1-11. |
| [2] |
HENNIG G, WELLER D, VIRNIG D, et al. SP-300 autopilot flight director system data for 737 flight crew training simulators: D637704[R]. USA: Boeing Company, D6-37704, 2006. |
| [3] |
LIAO F, WANG J, POH E, et al.
Fault-tolerant robust automatic landing control design[J]. Journal of Guidance, Control and Dynamics, 2005, 28(5): 854–871.
DOI:10.2514/1.12611
|
| [4] |
RAFI M, STECK J, ROKHSAZ K. A microburst response and recovery scheme using advanced flight envelope protection[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis, USA: AIAA, 2012: 1-13. |
| [5] |
MARCOS A, BALAS G.
Development of linear parameter varying models for aircraft[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(2): 218–228.
DOI:10.2514/1.9165
|
| [6] |
KRINGS M, THIELECKE F. An integrated approach to predictive flight guidance and envelope protection[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis, USA: AIAA, 2012: 1-13. |
| [7] |
HORN J, SAHANI N.
Detection and avoidance of main rotor hub moment limits on rotorcraft[J]. Journal of Aircraft, 2004, 41(2): 372–379.
DOI:10.2514/1.301
|
| [8] |
UNNIKRISHNAN S, PRASAD J. Carefree handling using reactionary envelope protection method[C]//AIAA Guidance, Navigation, and Control Conference. Keystone, USA: AIAA, 2006: 1-18. |
| [9] |
PAPAGEORGIOU G.Analysis and flight testing of a robust gain scheduling controller for the VAAC harrier[D]. Cambridge: University of Cambridge, 2000. |
| [10] |
BHATTACHARYA R, BALAS G, KAYA M, et al.
Nonlinear receding horizon control of an F-16 aircraft[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(5): 924–931.
DOI:10.2514/2.4965
|
| [11] |
陈虹.
模型预测控制[M]. 北京: 科学出版社, 2013.
CHEN Hong. Model predictive control[M]. Beijing: Science Press, 2013. |
| [12] |
HANKE C, NORDWALL D.The simulation of a jumbo jet transport aircraft volume Ⅱ: Modeling data: NASA, CR-114494[R]. USA: NASA, 1970. |
 2018, Vol. 50
2018, Vol. 50


