飞机在大气飞行时常遭遇阵风和紊流的干扰,这种干扰会使飞机气动升力面的有效攻角发生改变,进而引起升力突然改变,降低驾驶员和乘客的安全性及舒适性。阵风干扰在机体上引起的动态载荷还会降低机体寿命。因此,合理确定阵风载荷并减缓阵风影响对确保飞机安全飞行具有重大的意义[1]。
阵风载荷减缓(Gust load alleviation, GLA)的基本原理是通过传感器感受风场和飞机的运动状态,然后按照一定的规律操纵升降舵、对称襟翼等操纵面偏转,产生直接升力来减小阵风对飞行过载的影响[2]。针对阵风载荷减缓主动控制,国内外已做过许多研究。为了引入合适的阵风载荷,梁鉴和金华等分别设计了FL-12和FL-13两套阵风发生器[3, 4],朱博和吴志刚等对阵风发生器流场做了测量与分析[5, 6]。在控制器设计方面,主要有LQR/ LQG和H∞两种控制理论[7-13]。陈磊和吴志刚等还研究了多控制面机翼阵风减缓主动控制,并通过风洞实验进行了验证[14]。
目前,学者们针对阵风载荷减缓主动控制做了丰富的理论分析和数值仿真研究,但在风洞实验验证方面有待于完善。因此,本文设计了一套阵风载荷减缓主动控制实验系统,将数值仿真与风洞实验相结合,并引入了次最优和H∞控制器。H∞控制器在设计时考虑沉浮、俯仰方向的阻尼不确定因素以及超声电机建模时存在的误差,在风洞实验中展现出更优的控制效果。
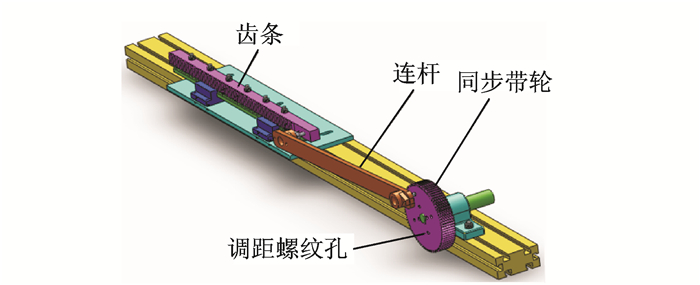
1 阵风发生器 1.1 阵风发生器结构设计阵风发生器可在垂直方向产生稳定的简谐流场[15], 它主要由驱动机构、叶栅摆动机构和控制系统等组成。驱动机构见图 1,主要包括同步带轮、连杆、齿条、导轨和滑块等。连杆与同步带轮、连杆与齿条均通过螺栓调心轴承连接。另外,在同步带轮上开有7组与轴心距离不同的螺纹孔,用以改变曲柄的长度,以达到改变叶栅最大摆角的目的。
|
图 1 阵风发生器驱动机构 Figure 1 Driving mechanism of gust generator |
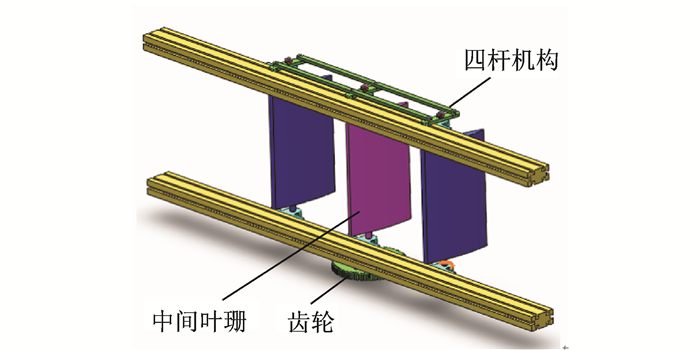
叶栅摆动机构见图 2,主要包括翼型、四杆机构以及用于驱动叶栅转动的齿轮。所采用叶栅为3组NACA0018的翼型,展长300 mm,弦长200 mm,叶栅轴心距离为300 mm。中间叶栅为主动叶栅,通过四杆机构带动两侧从动叶栅,实现同步运动。为保证叶栅高频摆动时的安全性,在另一侧增加一组连杆,形成对称的平行四边形。
|
图 2 阵风发生器叶栅摆动机构 Figure 2 Cascade swing of gust generator |
控制系统包括三相变频电机和变频器。三相变频电机接380 V交流电,功率为1.5 kW,具有恒功率调频和恒转速调频两种调速方式,变频器变频范围0~500 Hz。为获得电机转速与变频器调频的关系,在电机上加装光电编码器,以测量电机的转速。
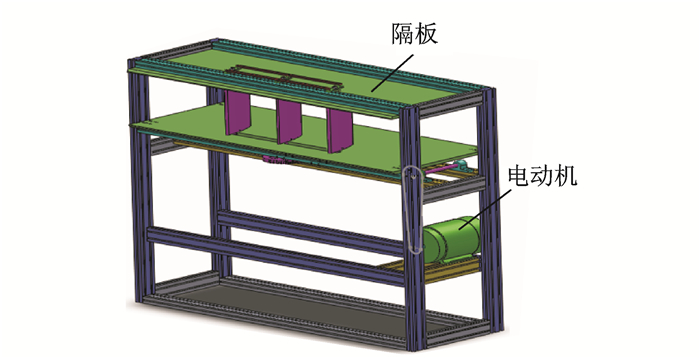
完整的阵风发生器如图 3所示。为了使经过叶栅摆动产生的流场具有更好的稳定性,在叶栅的两端还设立了两片平行隔离反射板,用来减少外部气流的干扰。
|
图 3 阵风发生器 Figure 3 Gust generator |
1.2 阵风发生器数值模拟
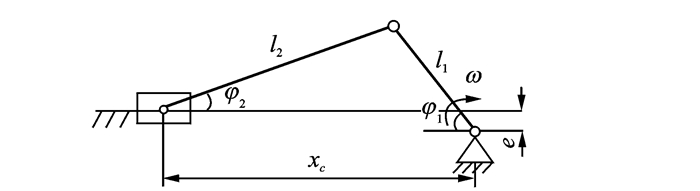
将传动机构等效为曲柄滑块机构,如图 4所示。
|
图 4 曲柄滑块机构 Figure 4 Slider-crank mechanism |
连杆l2长度400 mm,偏心距e1.47 mm,曲柄长度l1为可变长度,通过调整螺栓轴承到同步带轮轴心的距离实现,如图 5所示。

|
图 5 同步带轮 Figure 5 Synchronous pulley |
为增加叶栅的摆角范围,叶栅的驱动采用两种规格的齿轮,其模数相同,直径比为1:2。表 1为曲柄长度l1和叶栅摆角θ的对应关系。
| 表 1 曲柄长度与叶栅摆角 Table 1 The relation between crank length and blade angle |
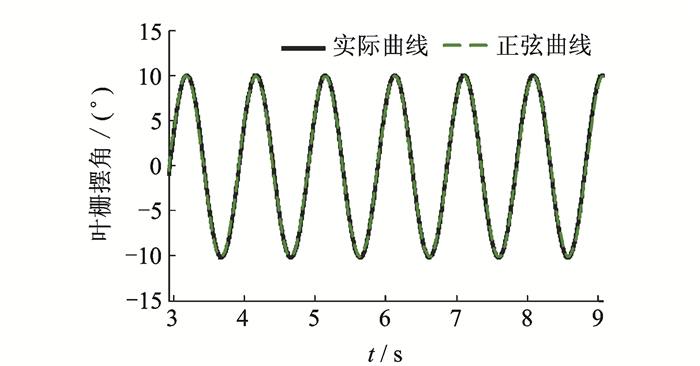
实验中由于传动机构存在较小的偏心距e=1.47 mm,叶栅为类简谐运动,但由于该偏心距相比曲柄和连杆的长度较小,叶栅的运动规律具有很好的简谐性。图 6为叶栅实际运动与正弦曲线10sin(2πt)的比对。
|
图 6 叶栅实际运动与正弦曲线 Figure 6 Actual and simulation motion of cascade |
2 气动弹性模型 2.1 二维翼段模型
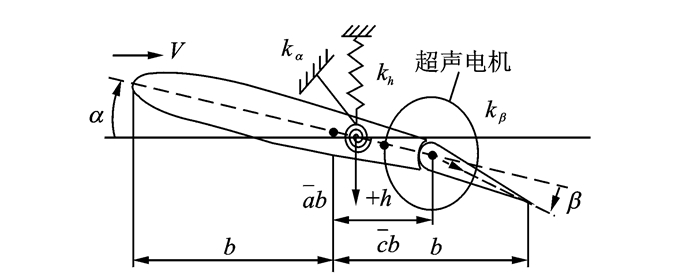
采用二维翼段作为实验模型,超声电机为作动器带动后缘控制面,如图 7所示。其中h为沉浮位移,向下为正,α为主翼俯仰角,顺时针为正,β为控制面转角,顺时针为正;b为半弦长,弹性中轴与弦中点的距离为b,控制面转轴到弦中点的距离为b;kh,kα和kβ分别为沉浮刚度、俯仰刚度以及控制面偏转刚度。a为弹性轴到弦中点的距离与半弦长的比值,c为控制面转轴到弦中点的距离与半弦长的比值。
|
图 7 二维翼段模型 Figure 7 2-D airfoil section model |
2.2 非定常气动力计算
基于Theodorsen定理,二维翼段做简谐运动受到的气动升力Lα和对弹性轴的气动力矩Tα分别为[2]
| $ \begin{array}{l} - {L_\alpha } = - {\rm{ \mathsf{ π} }}{\rho _{\rm{a}}}{b^2}{s_p} \times \\ \;\;\;\;\;\;\left[ {\ddot h + V\dot \alpha - b\bar a\ddot \alpha - {T_4}\dot \beta \frac{V}{{\rm{ \mathsf{ π} }}} - \frac{b}{{\rm{ \mathsf{ π} }}}{T_1}\ddot \beta } \right] + \\ \;\;\;\;\;\;2{\rm{ \mathsf{ π} }}{\rho _{\rm{a}}}Vb{s_p}C\left( k \right)\left[ {V\alpha + \dot h + b\left( {0.5 - \bar a} \right)\dot \alpha + } \right.\\ \;\;\;\;\;\;\left. {\frac{V}{{\rm{ \mathsf{ π} }}}{T_{10}}\beta + \frac{b}{{2{\rm{ \mathsf{ π} }}}}{T_{11}}\dot \beta } \right] \end{array} $ |
| $ \begin{array}{l} {T_\alpha } = {\rm{ \mathsf{ π} }}{\rho _{\rm{a}}}{b^2}{s_p}\left\{ {b\bar a\ddot h - Vb\left( {0.5 - \bar a} \right)\dot \alpha - } \right.\\ \;\;\;\;\;{b^2}\left( {0.125 + {{\bar a}^2}} \right)\ddot \alpha - \frac{{{V^2}}}{{\rm{ \mathsf{ π} }}}\left( {{T_4} + {T_{10}}} \right)\beta + \\ \;\;\;\;\;\frac{{Vb}}{{\rm{ \mathsf{ π} }}}\left[ { - {T_1} + {T_8} + \left( {\bar c - \bar a} \right){T_4} - 0.5{T_{11}}} \right]\dot \beta + \\ \;\;\;\;\;\left. {\left( {{b^2}/{\rm{ \mathsf{ π} }}} \right)\left[ {{T_7} + \left( {\bar c - \bar a} \right){T_1}} \right]\ddot \beta } \right\} + \\ \;\;\;\;\;2{\rm{ \mathsf{ π} }}{\rho _{\rm{a}}}V{b^2}{s_p}\left( {\bar a + 0.5} \right)C\left( k \right)\\ \;\;\;\;\;\left\{ {V\alpha + \dot h + b\left( {0.5 - \bar a} \right)\dot \alpha + \left( {V/{\rm{ \mathsf{ π} }}} \right){T_{10}}\beta + } \right.\\ \;\;\;\;\;\left. {\left( {b/2{\rm{ \mathsf{ π} }}} \right){T_{11}}\dot \beta } \right\} \end{array} $ | (1) |
式中:ρa为空气密度,V为来流风速,C(k)为Theodorsen函数,Ti(i=1, 4, 7, 8, 10, 11)为依赖于弾性轴位置和控制面铰链线性位置的Theodorsen常数。
基于Küsser函数和Duhamel积分,二维翼段在阵风干扰下的气动升力Lg和对弹性轴的气动力矩Tg分别为
| $ \begin{array}{*{20}{c}} {{L_{\rm{g}}} = 2{\rm{ \mathsf{ π} }}{\rho _{\rm{a}}}Vb\left[ {{\omega _{\rm{g}}}\left( t \right){\varphi _{\rm{g}}}\left( 0 \right) + \int_0^t {{\omega _{\rm{g}}}\left( \sigma \right)\frac{{{\rm{d}}{\varphi _{\rm{g}}}\left( {t - \sigma } \right)}}{{{\rm{d}}\sigma }}{\rm{d}}\sigma } } \right]}\\ {{T_{\rm{g}}} = 2{\rm{ \mathsf{ π} }}\left( {0.5 + a} \right)\rho V{b^2}\left[ {{\omega _{\rm{g}}}\left( t \right){\varphi _{\rm{g}}}\left( 0 \right) + } \right.}\\ {\left. {\int_0^t {{\omega _{\rm{g}}}\left( \sigma \right)\frac{{{\rm{d}}{\varphi _{\rm{g}}}\left( {t - \sigma } \right)}}{{{\rm{d}}\sigma }}{\rm{d}}\sigma } } \right]} \end{array} $ | (2) |
式中:ωg为阵风速度,φg(t)为Küssner函数,其表达式为[15]
| $ {\varphi _{\rm{g}}}\left( t \right) = 1 - {\delta _3}{{\rm{e}}^{\frac{{ - {\varepsilon _3}Vt}}{b}}} - {\delta _4}{{\rm{e}}^{\frac{{ - {\varepsilon _4}Vt}}{b}}} $ | (3) |
当用超声电机施加控制后,控制面的转角取决于超声电机输出轴的转角指令βc。
超声电机二阶动力学方程
| $ \ddot \beta + 2{\omega _0}\zeta \dot \beta + \omega _0^2\beta = {k_0}\omega _0^2{\beta _c} $ | (4) |
式中:β是超声电机的实际转角,k0是比例系数,ω0是固有频率,ζ为阻尼比。
包含超声电机作动特性在内的二维翼段气动弹性运动方程为
| $ {\mathit{\boldsymbol{M}}_{\rm{s}}}\ddot q + {\mathit{\boldsymbol{D}}_{\rm{s}}}\dot q + {\mathit{\boldsymbol{K}}_{\rm{s}}}\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{F}} + {\mathit{\boldsymbol{G}}_{\rm{s}}}{\mathit{\boldsymbol{\beta }}_{\rm{c}}} $ | (5) |
式中
| $ {\mathit{\boldsymbol{M}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} m&{{S_{h\alpha }}}&{{S_{h\beta }}}\\ {{S_\alpha }}&{{I_\alpha }}&{{S_{\alpha \beta }}}\\ 0&0&1 \end{array}} \right],{\mathit{\boldsymbol{D}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} {{d_h}}&0&0\\ 0&{{d_\alpha }}&0\\ 0&0&{{d_\beta }} \end{array}} \right],\mathit{\boldsymbol{q}} = \left\{ {\begin{array}{*{20}{c}} h\\ \alpha \\ \beta \end{array}} \right\} $ |
| $ {\mathit{\boldsymbol{K}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} {{k_h}}&0&0\\ 0&{{k_\alpha }}&0\\ 0&0&{{k_\beta }} \end{array}} \right],\mathit{\boldsymbol{F}} = \left\{ {\begin{array}{*{20}{c}} { - \left( {{L_\alpha } + {L_g}} \right)}\\ {{T_\alpha } + {T_g}}\\ 0 \end{array}} \right\},{\mathit{\boldsymbol{G}}_{\rm{s}}} = \left\{ {\begin{array}{*{20}{c}} 0\\ 0\\ {{g_0}} \end{array}} \right\} $ |
式中:m为二维翼段的质量,Shα为翼段对弹性轴的质量静矩,Shβ为控制面对其转动轴的质量静矩,Iα为翼段对弹性轴的转动惯量,Sαβ=(c-b)Shβ+Iβ,Iβ为控制面对其转动轴的转动惯量,dh,dα为相应阻尼系数,kh,kα为相应刚度系数。控制面偏转阻尼dβ=2ω0ζ,控制面偏转刚度kβ=ω02,g0=k0ω02。
加入阵风后二维翼段增广系统状态空间方程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{B}}{\beta _{\rm{c}}} + {\mathit{\boldsymbol{G}}_{\rm{g}}}{\omega _{\rm{g}}}\\ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}} \end{array} \right. $ | (6) |
式中:A为系统矩阵,B为控制面输入矩阵,Gg为阵风输入矩阵,C为输出矩阵,其中
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{\mathit{\boldsymbol{0}}_{3 \times 2}}}&{{\mathit{\boldsymbol{0}}_{3 \times 2}}}\\ { - {\mathit{\boldsymbol{M}}^{ - 1}}K}&{ - {\mathit{\boldsymbol{M}}^{ - 1}}D}&{ - {V^2}{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{E}}_{\rm{c}}}}&{{V^2}{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{E}}_{\rm{g}}}}\\ {V{\mathit{\boldsymbol{K}}_\alpha }}&{{\mathit{\boldsymbol{D}}_\alpha }}&{V{\mathit{\boldsymbol{Q}}_\alpha }}&{{\mathit{\boldsymbol{0}}_{2 \times 2}}}\\ {{\mathit{\boldsymbol{0}}_{2 \times 3}}}&{{\mathit{\boldsymbol{0}}_{2 \times 3}}}&{{\mathit{\boldsymbol{0}}_{2 \times 2}}}&{V{\mathit{\boldsymbol{A}}_{\rm{g}}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{B}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{0}}_{3 \times 1}}\\ {\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{G}}_{\rm{s}}}\\ {\mathit{\boldsymbol{0}}_{4 \times 1}} \end{array} \right],{\mathit{\boldsymbol{G}}_{\rm{g}}} = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{0}}_{8 \times 1}}}\\ 1\\ 1 \end{array}} \right\} $ |
| $ \mathit{\boldsymbol{C}} = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{0}}_{1 \times 2}}}&1&1&1&{{\mathit{\boldsymbol{0}}_{3 \times 2}}} \end{array}} \right\} $ |
式中:状态变量
由于所有气动力状态变量并不是都可测的,最优控制难以实现,本文采用基于输出反馈最优方法设计次最优控制器。反馈信号为3组可测信号:沉浮位移h、俯仰角α和控制面偏转角β。受控动力学方程为
| $ {\beta _{\rm{c}}} = - {\mathit{\boldsymbol{K}}_{{\rm{con}}}}\mathit{\boldsymbol{Y}} = - {\mathit{\boldsymbol{K}}_{{\rm{con}}}}\mathit{\boldsymbol{CX}} $ | (7) |
式中:βc为控制面转角输入量,设计次最优控制律就是寻求次最优反馈矩阵Kcon,使目标函数J达到极小,即有
| $ J = \frac{1}{2}\int_0^\infty {\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{QX}} + p\beta _{\rm{c}}^2} \right){\rm{d}}t} $ | (8) |
式中:Q为半正定加权矩阵,p>0为加权系数。Q由最小范数法求得。次最优反馈矩阵Kcon为
| $ {\mathit{\boldsymbol{K}}_{con}} = {\mathit{\boldsymbol{F}}^ * }{\mathit{\boldsymbol{C}}^{\rm{T}}}{\left( {{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}} \right)^{ - 1}} $ | (9) |
式中:F*为常增益全状态反馈矩阵,由LQR控制求出。
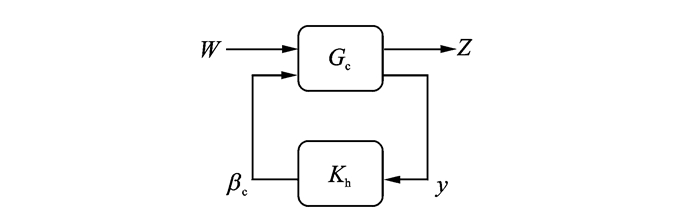
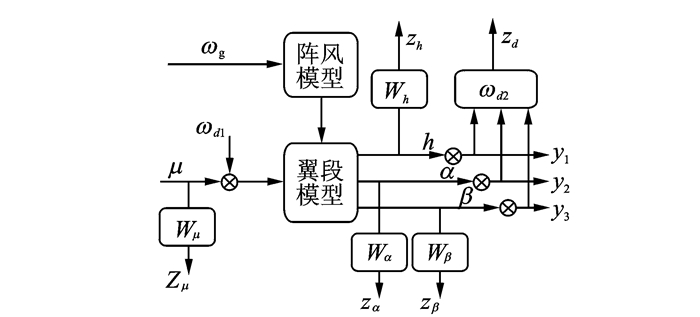
3.2 H∞控制器设计本文设计的另一种控制器采用的是乘法摄动模型的H∞控制器。图 8和图 9分别为标准H∞控制系统和转换后的翼段模型H∞控制系统模块图。其中:ωg为加载的阵风速度,u为控制输入,y1, y2和y3为3组测量信号,即沉浮位移、俯仰角和控制面转角。Wh, Wα和Wβ和分别表示机翼沉浮、俯仰和控制面偏转方向的乘法摄动大小,Wμ为用来调整输入大小的加权函数,ωd1用于调节输入的响应速度,ωd2为干扰的动态特性,zh, zα, zβ, zu和zd是保证乘法摄动鲁棒性的评价信号。
|
图 8 标准H∞控制系统 Figure 8 Standard H∞ control block system |
|
图 9 阵风载荷减缓H∞控制系统模型 Figure 9 H∞ control block of GLA |
4 数值仿真
表 2为模型实际参数及风洞实验条件参数。Sp为二维翼段的展长,其他参数定义见上文。
| 表 2 仿真参数 Table 2 Simulation parameter |
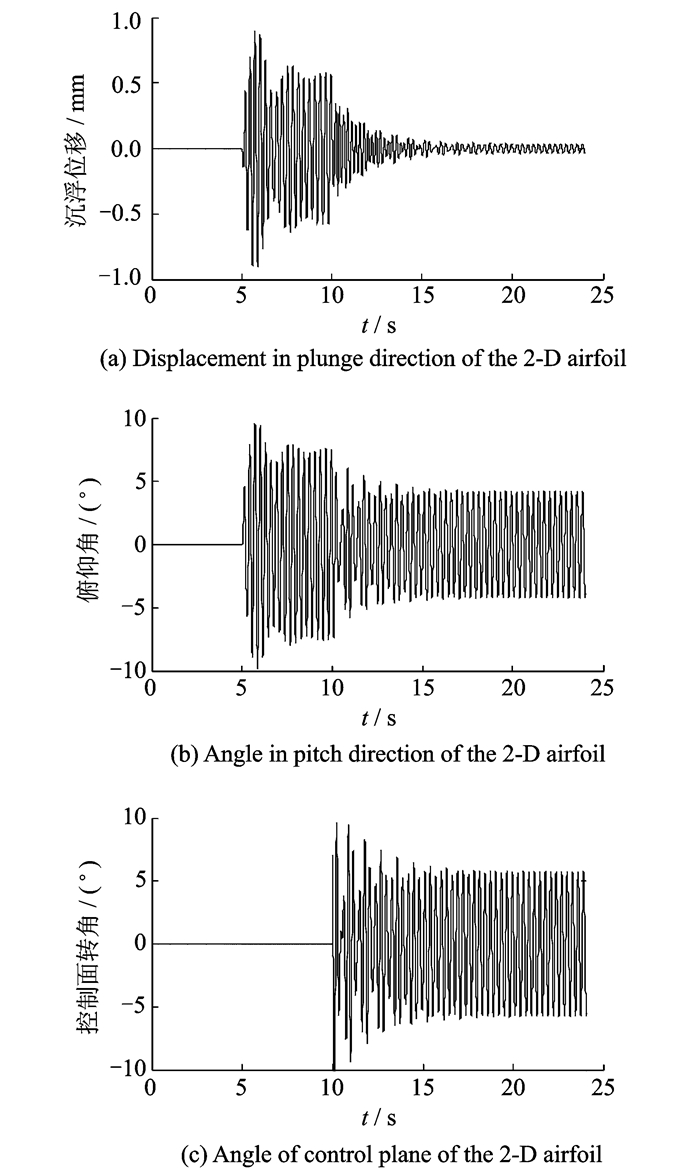
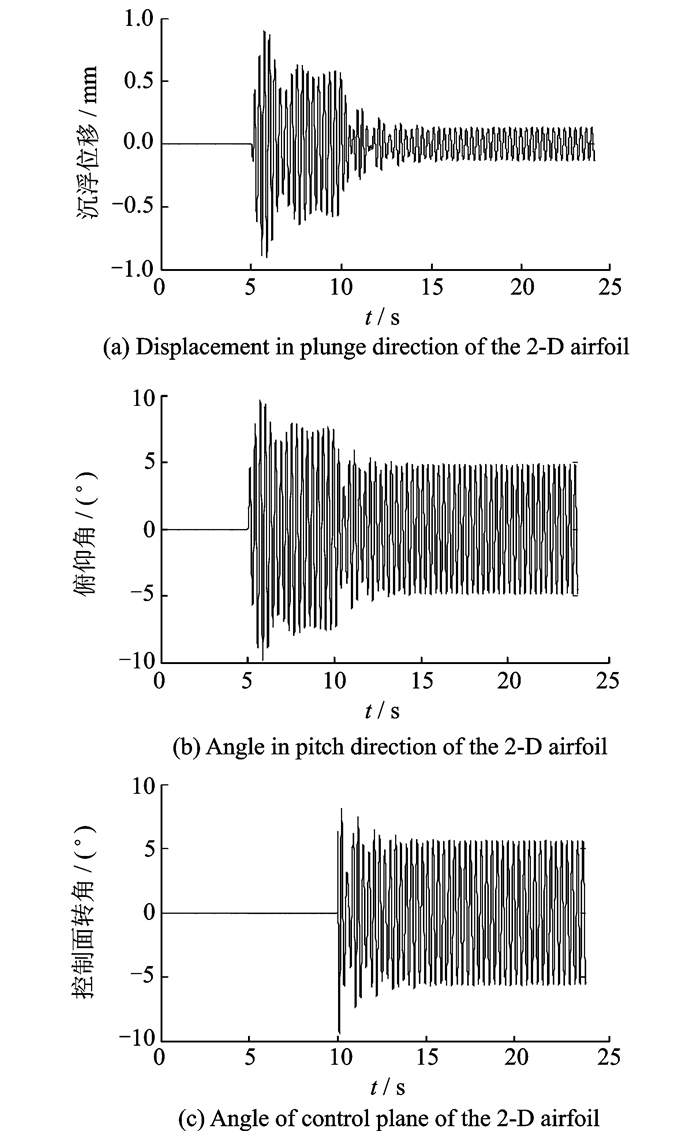
图 10, 11为来流风速为12 m/s,阵风速度峰值为2.5 m/s,阵风频率为3 Hz时,翼段的阵风响应及施加次最优控制器和H∞控制器后的结果。
|
图 10 次最优控制器仿真控制效果 Figure 10 Simulation of GLA in suboptimal controller |
|
图 11 H∞控制器仿真控制效果 Figure 11 Simulation of GLA in H∞controller |
仿真结果表明:两种控制器均可以减缓阵风载荷。如图 10和图 11,在翼段响应后的10 s施加控制器,次最优控制器和H∞控制器可有效减小机翼沉浮位移和俯仰角的阵风响应幅值,沉浮位移方向可以明显看出次最优控制器在减缓效果上比H∞控制器要更好;在俯仰方向次最优控制器的减缓效果也比H∞控制器好;两控制器所输出的控制面转角均在±10°范围内且最终保持稳定。
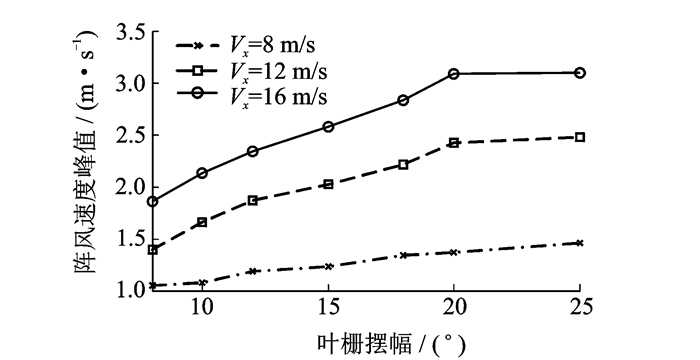
5 风洞实验 5.1 实验装置采用PIV流场测量设备对二维翼段轴线位置处的阵风速度峰值进行了测量。图 12为3组来流风速下,叶栅摆幅与阵风速度峰值的对应关系。可以发现:在一定来流风速范围内且叶栅摆幅不大时,阵风速度峰值与叶栅摆幅基本呈线性关系。
|
图 12 阵风速度峰值与叶栅摆幅对应关系 Figure 12 The relation between gust amplitude and cascade swing amplitude |
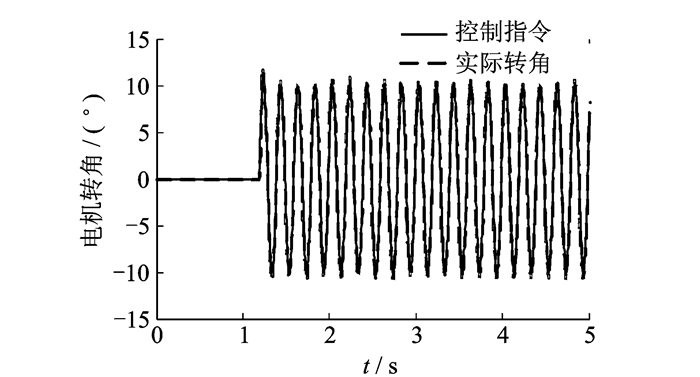
采用超声电机驱动后缘控制面,超声电机采用PID控制。图 13为超声电机对正弦信号10sin(2π·5t)的跟随效果。
|
图 13 超声电机跟随效果 Figure 13 The motion of ultrasonic motor |
图 14为整套实验装置及风洞,左侧为风洞口,接阵风发生器,阵风发生器后接二维翼段,二维翼段垂直放置,固定于安装架。阵风发生器及二维翼段的上下端部都安装有稳定流场的隔离反射板。本实验在南京航空航天大学空气动力学实验室完成。风洞开口试验段截面为矩形1.5 m×1 m,试验段长度1.7 m,最大风速40 m/s,湍流度0.08%。

|
图 14 阵风实验装置及风洞 Figure 14 The experimental device and tunnel |
实验中,首先开风洞,加载稳定的来流风速。此时,翼段不会发生振动。然后开阵风发生器,阵风发生器从静止到按设定的频率运动需要几秒的时间,这是翼段逐渐加载的过程。阵风发生器运行至稳定,翼段以固定的频率和幅值运动。最后施加控制,翼段到达另一个稳定运动的状态。
5.2 实验结果风洞实验结果表明:当阵风频率为1~6 Hz、来流风速5~25 m/s时,次最优控制器或H∞控制器对阵风载荷均有很好的减缓效果,尤其是当阵风频率在3.36 Hz和5.19 Hz附近时,此时减缓效果最为明显。因为所采用的二维翼段沉浮方向和俯仰方向的固有频率分别为3.361 Hz和5.191 Hz,此时,二维翼段受阵风干扰发生共振现象。但是,当阵风频率小于1 Hz或高于6 Hz或来流风速小于5 m/s时,由于翼段本身受阵风载荷影响比较小,此时减缓效果并不明显。
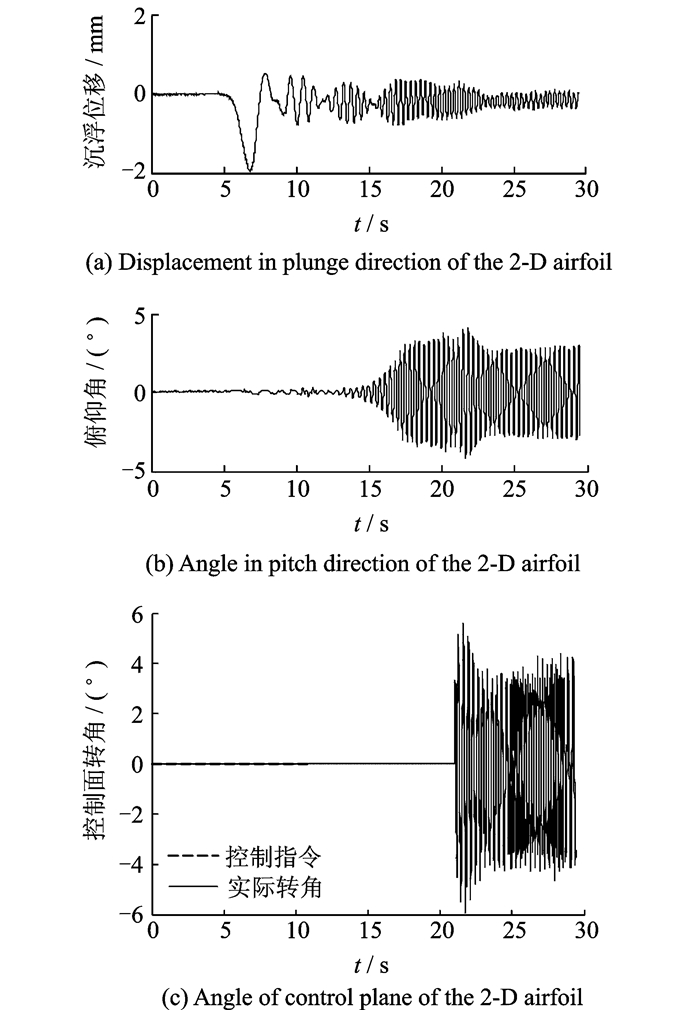
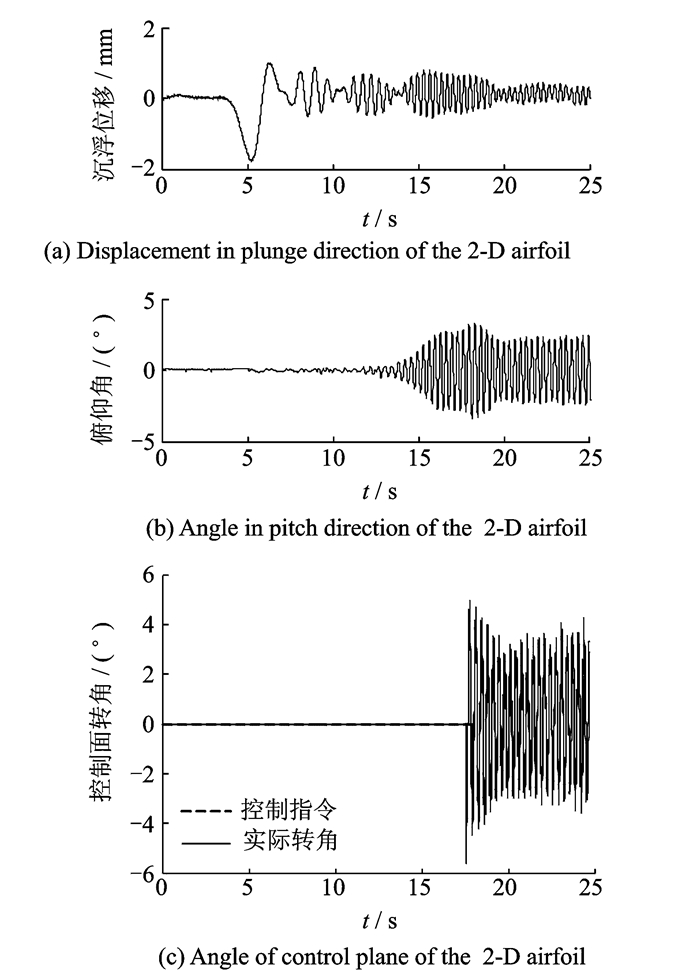
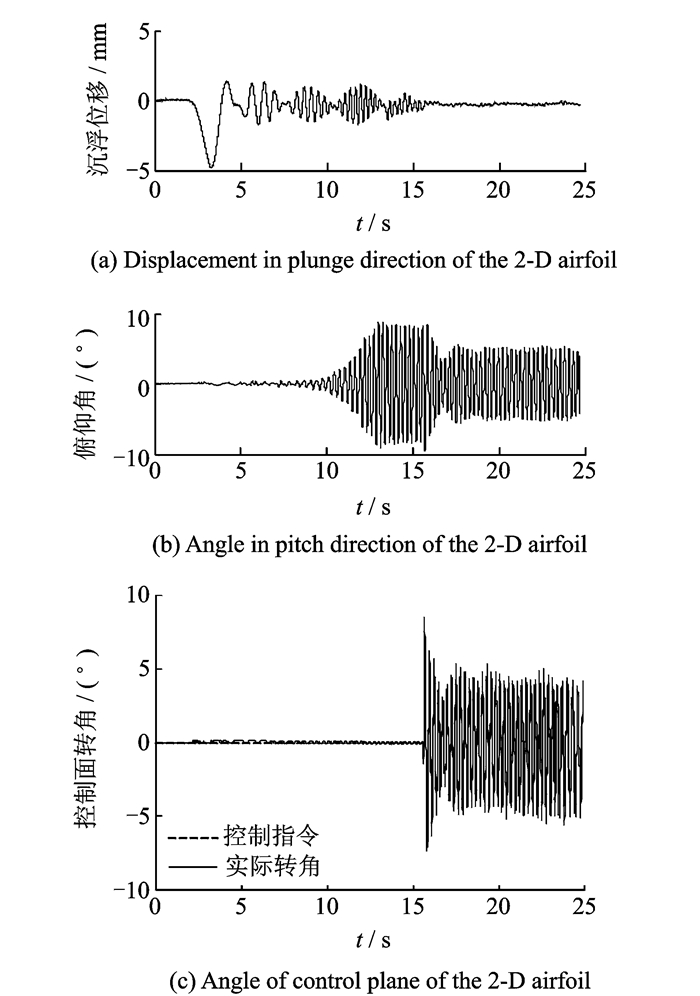
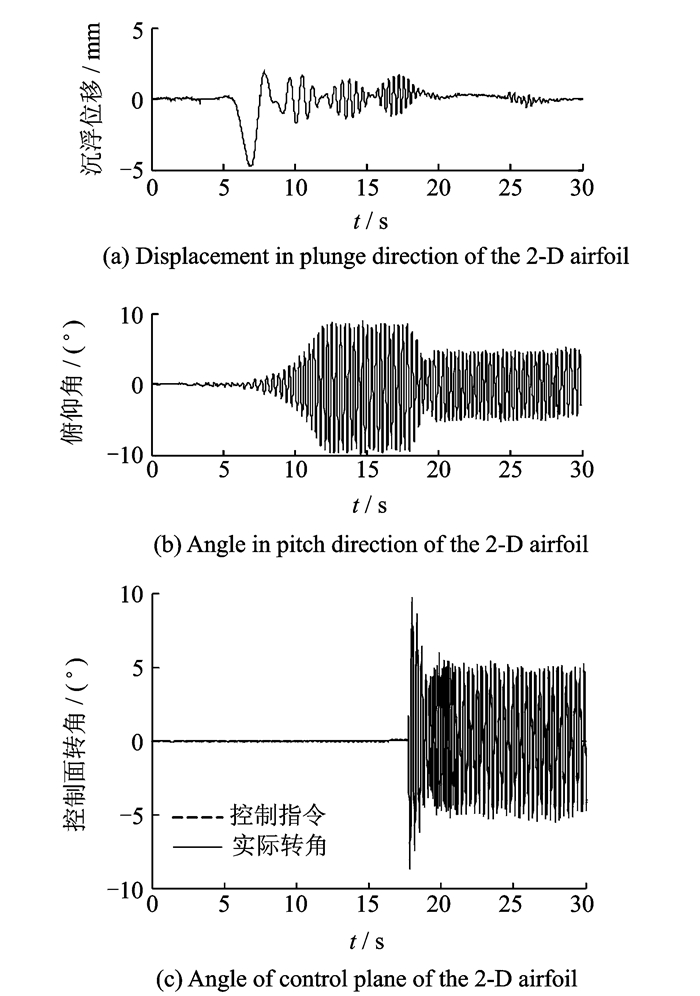
图 15—图 18为来流风速为12 m/s,阵风速度峰值为2.5 m/s,阵风频率分别为3 Hz,3.3 Hz的实验结果。图 15和图 16为次最优控制、图 17和图 18为H∞控制下的实验结果。
|
图 15 f=3 Hz次最优控制器风洞实验控制 Figure 15 Effect of suboptimal controller at f=3 Hz |
|
图 16 f=3.3 Hz次最优控制器风洞实验控制 Figure 16 Effect of suboptimal controller at f=3.3 Hz |
|
图 17 f=3 Hz H∞ 控制器实验控制效果 Figure 17 The effect of H∞ controller at f=3 Hz |
|
图 18 f=3.3 Hz H∞ 控制器实验控制效果 Figure 18 The effect of H∞ controller at f=3.3 Hz |
定义阵风载荷减缓效率
| $ r = \frac{{{x_0} - {x_1}}}{{{x_0}}} \times 100\% $ | (10) |
式中:x0为未加控制时,加载阵风载荷稳定后翼段沉浮方向或俯仰方向阵风响应的最大幅值,x1则为加入控制后翼段沉浮方向或俯仰方向阵风响应的最大幅值。
表 3为固定阵风速度幅值为2.5 m/s和来流风速为12 m/s,阵风频率分别为3, 3.3, 5.1和7 Hz时,统计出次最优控制器和H∞控制器分别在仿真和实验时阵风载荷减缓的平均效率并作对比。
| 表 3 阵风载荷减缓平均效率对比 Table 3 Comparison of GLA efficiency |
仿真结果和实验结果同时表明:两种控制器均可以减缓阵风载荷,通过对比发现:仿真中次最优控制器比H∞控制器具有更好的阵风载荷减缓效果,但实验中H∞控制器比次最优控制器效果更好,且实验结果和仿真结果更加接近。这是因为次最优控制在设计时,当阵风载荷和翼型参数严格确定之后,最优化的设计控制器,最大程度的减缓阵风载荷。而H∞控制在设计时,考虑了沉浮方向和俯仰方向的阻尼不确定因素以及超声电机建模时存在的误差,提高了模型对动态干扰的鲁棒性,实际控制效果优于次最优控制器。此外次最优控制器的控制率是根据3组可测的反馈信号即沉浮位移h、俯仰角α和控制面偏转角β实时计算出的,但在实验环境下传感器采集的数据中含有噪声、时滞等影响且实验参数存在测量误差,所以次最优控制器的实际控制效果相比仿真结果有一定的偏差。
6 结束语本文采用二维翼段作为阵风载荷减缓主动控制的研究对象,设计了一套完整的实验系统。将数值仿真与风洞实验相结合,实际验证了阵风载荷减缓效果。风洞实验结果表明:两种控制器均能对阵风载荷起到减缓的作用,但通过对比两种控制器的阵风载荷减缓效率发现:H∞控制器比LQR控制器具有更优的载荷减缓效果,且实验结果与仿真结果更加接近。因为H∞控制器设计时,考虑了沉浮方向、俯仰方向的阻尼不确定因素以及超声电机建模时存在的误差,提高了模型对动态干扰的鲁棒性。
| [1] |
莱特J R, 库珀J E.
飞机气动弹性力学及载荷导论[M]. 上海: 上海交通大学出版社, 2011.
WRITE J R, COOPER J E. Introduction to aircraft aeroelasticity and loads[M]. Shanghai: Shanghai Jiao Tong University Press, 2011. |
| [2] |
赵永辉, 黄锐.
高等气动弹性力学与控制[M]. 北京: 科学出版社, 2015.
ZHAO Yonghui, HUANG Rui. Advanced aeroelasticity and control[M]. Beijing: Science Press, 2015. |
| [3] |
梁鉴, 唐建平, 杨远志.
FL-12风洞突风试验装置研制[J]. 实验流体力学, 2012, 26(3): 95–100.
DOI:10.3969/j.issn.1672-9897.2012.03.018 LIANG Jian, TANG Jianping, YANG Yuanzhi. The development of gust generators in FL-12 wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 95–100. DOI:10.3969/j.issn.1672-9897.2012.03.018 |
| [4] |
金华, 王辉, 张海酉, 等.
FL-13风洞突风发生装置研究[J]. 空气动力学学报, 2016, 34(1): 41–46.
JIN Hua, WANG Hui, ZHANG Haiyou, et al. Investigation on gust response test apparatus in FL-13 wind tunnel[J]. Acta Aerodynamic Sinica, 2016, 34(1): 41–46. |
| [5] |
朱博, 刘琴, 屈晓力, 等.
阵风发生装置流场测量与分析[J]. 实验流体力学, 2013, 27(6): 77–80.
ZHU Bo, LIU Qin, QU Xiaoli, et al. Measurement and analysis of a gust generator flow field in wind[J]. Journal of Experiment in Fluid Mechanics, 2013, 27(6): 77–80. |
| [6] |
刘晓燕, 吴志刚, 杨超, 等.
阵风发生器流场特性分析与试验验证[J]. 北京航空航天大学学报, 2010, 36(7): 804–807.
LIU Xiaoyan, WU Zhigang, YANG Chao, et al. Flow field analysis and experimental investigation on gust generator[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(7): 804–807. |
| [7] |
BABBAR Y, SURYAKUMAR V S, STRGANAC T W. Measurement and modeling of nonlinear aeroelastic response under gust[C]//33rd AIAA Applied Aeronautics Conference. Dallas, TX: [s.n.], 2015. |
| [8] |
DILLSAVER M, CESNIK C, KOLMANOVSKY I. Gust load alleviation control forvery flexible aircraft[C]//AIAA Atmospheric Flight Mechanics Conference. Portland, Oregon: [s.n.], 2011. |
| [9] |
FEDERICO F, SERGIO R, PAOLO M.
Gust load alleviation for a regional aircraft through a static output feedback[J]. Journal of Aircraft, 2015, 52(5): 1559–1574.
DOI:10.2514/1.C032995
|
| [10] |
MOULIN B, KARPEL M.
Gust loads alleviation using special control surfaces[J]. Journal of Aircraft, 2007, 44(1): 17–25.
DOI:10.2514/1.19876
|
| [11] |
HAGHIGHAT S, LIU H H T, MARTINS J R R A. Application of model predictive control to gust load alleviation systems[C]//AIAA Atmospheric Flight Mechanics Conference.[S.l.]: AIAA, 2009. |
| [12] |
谭智勇, 安锦文.
H∞控制理论在阵风缓和控制中的应用[J]. 火力与指挥控制, 2005, 30(3): 94–95.
TAN Zhiyong, AN Jinwen. Application of H∞ theory to gust load alleviation control[J]. Fire Control and Command Control, 2005, 30(3): 94–95. |
| [13] |
张军红, 李振水, 詹孟权.
LQG控制理论在阵风载荷减缓系统中的应用[J]. 飞行力学, 2007, 25(2): 61–64.
DOI:10.3969/j.issn.1002-0853.2007.02.016 ZHANG Junhong, LI Zhenshui, ZHAN Mengquan. Application of LQG theory to gust load alleviation system[J]. Flight Dynamics, 2007, 25(2): 61–64. DOI:10.3969/j.issn.1002-0853.2007.02.016 |
| [14] |
陈磊, 吴志刚, 杨超.
多控制面机翼阵风减缓主动控制与风洞试验验证[J]. 航空学报, 2009, 30(12): 2250–2256.
DOI:10.3321/j.issn:1000-6893.2009.12.002 CHEN Lei, WU Zhigang, YANG Chao. Active control and wind tunnel test verification of multi-control surface wing for gust alleviation[J]. Acta Aeronautic Et Astronautica Sinica, 2009, 30(12): 2250–2256. DOI:10.3321/j.issn:1000-6893.2009.12.002 |
| [15] |
BISPLINGHOFF R L, ASHLEY H, HALFMAN R L.
Aeroelasticity[M]. New York: Dover Addison Wesley, 1995.
|
 2018, Vol. 50
2018, Vol. 50


