机场离港过程的场面交通拥堵不仅影响场面运行效率,加大调度员的工作负担,也造成大量的燃油浪费以及废气排放。当前飞机的进离港地面运行时间占总航行时间的10%~30%[1],主要原因是因为调度不流畅导致大量排队等待时间。飞机离港过程主要包括推出、滑行和起飞,适时地进行飞机推出有助于减少滑行排队等待时间,因此合理的飞机推出控制策略是减少机场场面拥堵的有效途径。
离港过程可以抽象为一个排队过程,Idris等[2]分析了影响离港过程的主要因素和离港队列的特点,通过预测离港滑行时间来合理安排推出时隙。Carr等[4]通过对波士顿机场交通流量的研究,在一些特定交通管制约束基础上提出了一种推出序列控制方法。Madas等[4]、Vossen等[5]和高强等[6]分别对机型选择、时隙分配以及协同决策机制下自由指派时隙等方面进行了研究。Madas等[7]通过具体的机场结构,用整数规划的方法来选择和分配推出时隙。Liu等[7]提出了一种基于离散差分进化的推出时隙分配策略来优化推出成本。Pujet等[8]通过分析跑道系统结构和历史运行数据,提出一种混合排队模型使机场在低容量状态下降低离港滑行排队时间。Cheng等[9]针对推出计划的制定用动态规划的方法开发了一种支持工具来减少滑行过程中的停车次数。Roling等[10]用混合整数线性规划的方法对离港过程进行优化来减少地面延误和场面拥堵。Feron等[11]提出了一种队长阈值控制方法(N-control):若滑行道上离港飞机排队数超过一个阈值,其他飞机的推出申请将被拒绝,直到排队数小于阈值,这是一种离港推出率控制策略,策略的推出效果由队长阈值决定。Simaiakis等[12-13]在波士顿机场对N-control策略进行测试,并以成本为目标对N-control方法进行动态优化,对最优滑行道排队阈值进行研究。Martinez等[14]通过研究登机口等待时间的分配方法对N-control策略进行了扩展。在N-control策略的基础上,张亚平等[15]提出了这一种线性动态推出控制策略(Dynamic pushback control, DPC),即要求策略可以使推出率由队长阈值和当前滑行道排队长度同时决定,更加有效的控制离港过程总成本。
当前DPC策略的核心是寻找最优的滑行道队长阈值,这个阈值既要降低离港过程的排队拥堵,又要保证跑道和滑行道利用率,其状态为当滑行道排队长度较小时,保持较大的推出率,但随着排队长度的增加,推出率呈线性降低趋势,直到排队长度达到阈值时降为0。然而这种动态推出策略并非最优的动态推出策略,本文提出了动态推出策略的一般形式,并设计了一种基于网格参数搜索的蒙特卡洛仿真方法,探寻最优的动态推出策略,更加有效地将飞机的滑行排队等待时间转化为停机位等待时间,以降低机场离港运营成本,通过与DPC策略对比来验证其有效性。
1 机离港推出控制策略 1.1 飞机离港过程的描述与基本假设飞机离港主要过程包括推出、滑行和起飞,飞机的推出时刻选择直接影响着机场场面运行状态以及离港成本。飞机经过航食补充、旅客登机等过程后关闭舱门,飞行员向塔台提出推出请求,当收到推出指令后,飞机由牵引车牵引,之后进入滑行道滑行进而起飞。飞机处于不同的过程将产生相应的成本:处于登机口或停机位时,若延迟推出会因占用登机口或停机位而会降低滑行道和跑道的利用率,产生资源占用成本及利用率降低成本;飞机推出后处于滑行道时会产生燃油消耗成本,尤其在滑行道有较多飞机进行排队时,长时间等待造成大量燃油消耗成本。为了简化控制策略以及便于不同策略间的对比,在不影响适用性的前提下提出如下假设:
(1) 忽略天气因素及进港飞机的影响;
(2) 推出以及起飞过程采取先到先服务规则;
(3) 为了在同等条件下对比策略效果,采用固定跑道服务时间。
1.2 推出率控制策略当前已有的DPC策略的推出率随当前滑行道排队长度的增加而减小,其推出率为
| $ \lambda '{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {\lambda \left( {1 - \frac{n}{N}} \right)}&{n < N}\\ 0&{n \ge N} \end{array}} \right. $ |
式中:λ′为推出率;λ为推出请求率;n为当前滑行道排队长度;N为滑行道队长阈值。本文提出两种混合动态推出控制的策略,分别为阶梯函数控制策略(Step function, SPC)和非线性函数控制策略(Nonliner function, NPC)。两种推出策略的推出率分别为
| $ {\rm{SPC:}}{{\lambda '}_{\rm{2}}} = \left\{ \begin{array}{l} \lambda \;\;\;\;n \le {\theta _1}N\\ \alpha \lambda \;\;{\theta _1}N < n \le {\theta _2}N\\ \beta \lambda \;\;{\theta _2}N < n \le N\\ 0\;\;\;\;\;n > N \end{array} \right. $ |
| $ {\rm{NPC:}}{{\lambda '}_3} = \left\{ {\begin{array}{*{20}{c}} {\lambda \left[ {1 - \left( {\frac{n}{{\tau N}}} \right)} \right]}&{n < \min \{ N, \tau N\} }\\ 0&{n \ge \min \{ N, \tau N\} } \end{array}} \right. $ |
式中:α,β,θ1,θ2,σ,τ表示待确定参数,其中α,β,θ1,θ2∈(0, 1),且α>β,σ∈(0, 3]为非线性参数,τ∈(0, 3]为线性系数,τN为NPC策略的滑行道排队长度有效阈值,当τ < 1时产生此有效阈值,原因为需要保证当τ < 1时λ3'取值非负。σ和τ的取值范围是因为若两者超过3,推出率将接近于1,达不到控制效果。因此,待优化的3种策略包含最优队长滑行道队长阈值N及其对应参数。
由推出策略的形式可见,SPC策略随着当前滑行道排队长度n逐渐增加,推出率以阶梯函数形式变化,这种控制方法的特点是在滑行道排队长度在一定范围内时,推出频率恒定不变,很大程度上减少调度者的工作负担;对于NPC策略,σ=1时,推出率呈线性变化,而当τ=1时,推出率呈非线性变化;σ和τ取值越大,推出率约接近1,即转化为N-control策略,这种控制方法和DPC策略一样,推出率根据滑行道排队长度的变化而实时变化,但NPC策略可以通过参数寻优达到最优离港成本。推出策略通过推出率将拒绝一部分申请推出的飞机,使其停留在登机口以减少滑行道排队长度,而由于登机口等待的飞机增加,导致登机口资源的占用及滑行道利用率的降低。因此,策略对占用登机口的飞机给予一个惩罚因子,同时也用以弥补滑行道利用率降低带来的损失。
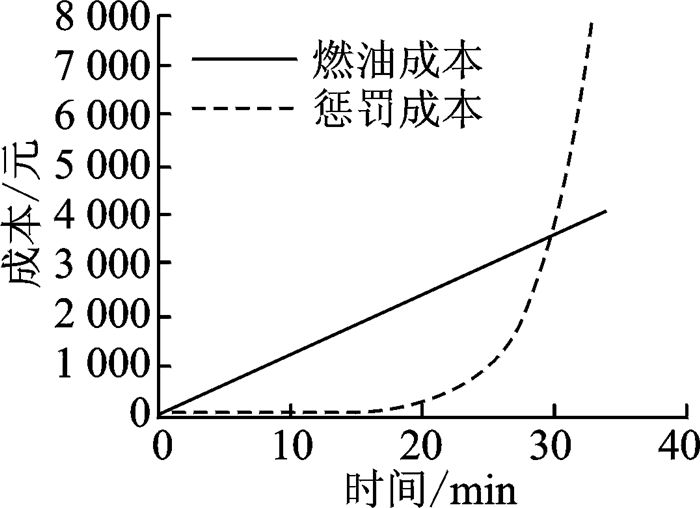
2 动态推出控制模型 2.1 目标函数当飞机的推出申请被拒绝时,需要停留在登机口等待下一次推出申请,以降低滑行燃油成本。然而,如果登机口资源占用时间过长,无疑会降低登机口利用率以及跑道利用率。因此策略对登机口停留时间引入一个惩罚项,惩罚项要求随着登机口停留时间的增长,并且停留时间越长,惩罚系数越高。基于这个特点,此处选择指数函数P=etρ作为惩罚项。根据中国民航局[16]准点率报告中对准点/晚点的定义:若一架航班在计划起飞时间之后的30 min以内完成起飞,即认为该航班准点放行;反之即为晚点。因此令燃油成本和惩罚成本在登机口停留时间G=30 min处相等,当登机口停留时间小于30 min时,惩罚成本小于同等时间下的燃油成本,一旦登机口停留时间超过30 min,惩罚成本急剧上升。燃油和惩罚成本如图 1所示。
|
图 1 燃油成本及惩罚成本曲线 Figure 1 Fuel-burn and gate-hold costs as a function of time |
图 1中,燃油成本的斜率由数据采集日期油价计算得到,令燃油成本曲线和惩罚成本曲线在停机位等待时间为30 min处相交,惩罚成本系数由式(1)得到
| $ \rho = \frac{{\ln \left( {ct + 1} \right)}}{t} $ | (1) |
式中:ρ表示惩罚因子;c表示每分钟滑行燃油成本;t表示燃油和惩罚成本平衡点时间。推出策略的目标函数为总成本最小,记为
| $ \min {C_{\rm{T}}} = \sum\limits_{i = 1}^M {c \cdot {W_i} + \left( {{{\rm{e}}^{\rho \cdot {G_i}}} - 1} \right)} $ | (2) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\;{\lambda _i} = \{ {{\lambda '}_{1, i}}, {{\lambda '}_{2, i}}, {{\lambda '}_{3, i}}\} $ | (3) |
| $ 0 \le n \le N $ | (4) |
| $ {G_i} \le 30 $ | (5) |
式中:i表示申请推出飞机;M表示离港飞机总数;W表示滑行时间;G表示登机口等待时间。式(2)为目标函数,由滑行燃油成本和停机位等待惩罚两部分组成;式(3)为推出率集,飞机i的推出过程由式(3)决定;式(4)为滑行道排队长度约束;式(5)为延误约束。
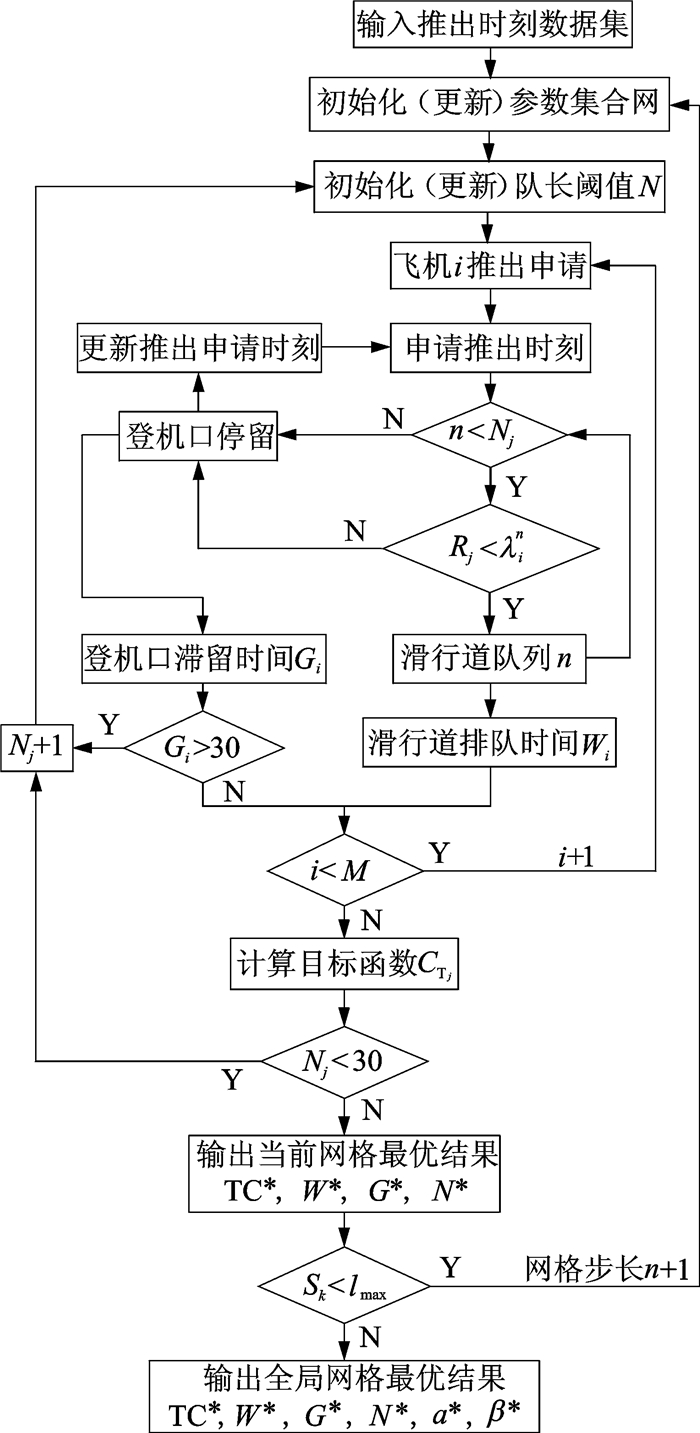
2.2 基于网格搜索的蒙特卡洛仿真方法受飞行计划、机场场面运行状态等众多因素影响,航班的申请推出时刻为随机变量,因此采用蒙特卡洛仿真的方法对航班离港过程进行仿真,由于目标函数是经过一系列航班离港流程仿真后计算得到,过程比较复杂,为避免出现重大误差,这里采用网格搜索法进行参数寻优,求解流程如图 2所示。
|
图 2 基于网格寻优的推出控制策略蒙特卡洛仿真流程图 Figure 2 Monte Carlo simulation flowchart of pushback control strategy based on gridding optimization |
图 2中滑行道最大排队允许长度根据滑行道有效长度和滑行飞机间距计算取30;R为蒙特卡洛随机数集合且Ri∈(0, 1),用来模拟推出概率,R服从均匀分布,例如当N=10,n=3时,下一架飞机的推出概率为(1-n/N)=0.7。此时进行判断,若随机数Rj < 0.7,即为“准许推出”;反之则“拒绝推出”。为方便各策略之间的控制效果对比,所有推出策略均使用同一随机数据集。算法中的网格为一个参数集,如NPC策略的一个网格为{τi, σj},网格精度为0.012,则“当前网格”表示参数为{τi, σj}时的离港过程循环。“全局网格”指能搜索空间内的所有{τ, σ}集。网格总数记为lmax,网格搜索步长为搜索精度。利用网格搜索的方法可以遍历整个解空间的所有参数组合,因此可以得到精确解。当飞机i的推出申请由于滑行道队长达到阈值或频率控制被拒绝时,它将停留在登机口等待1 min后进行下一次申请,直到被推出进入滑行道进而起飞。此期间,登机口的停留时间和滑行道的滑行时间将被输出用于目标函数的计算。当一个滑行道队长阈值N的循环进行完毕或者系统检测到某架飞机的停机位停留时间Gi>30 min,将赋予结果一个较大值并立刻对队长阈值更新进行下一个循环。当一个网格的离港过程仿真完毕(i=M)时,输出当前最优结果,开始下一个网格的循环,直到所有网格参数下的离港过程仿真完毕后,输出全局最优成本CT*及其对应的队长阈值N*、停机位停留时间G*、滑行道滑行时间W*和网格参数σ*和τ*。
3 实例分析 3.1 策略仿真为了探寻最优的动态推出策略,使用蒙特卡洛仿真的方法根据实际离港数据进行仿真寻优。北京首都机场包括01/19,18L/36R和18R/36L3条跑道,其中18L/36R跑道为主起飞跑道,因此仿真数据取2013年11月15日北京首都机场18L/36R跑道的推出申请数据集。由于推出控制策略在航班密集时间段的效果明显,因此以6:00至22:00为仿真时间窗。仿真采用MATLAB 2015b软件,滑行耗油成本参数根据数据采集日期油价以及首都机场离港所有机型的当量滑行燃油消耗量计算得c=120元/min,根据式(1)计算得惩罚因子ρ=0.273,为方便不同推出策略之间的结果对比,跑道服务时间(尾流间隔)采取固定值v=1.7 min,时间窗内离港飞机总数M=498架,由于仿真时间限制,两种策略的参数寻优网格精度分别设定为0.1和0.01。部分高峰期推出申请时间数据如表 1所示。
| 表 1 7:00 am至7:30 am(高峰期)推出申请时刻 Table 1 Pushback requests from 7:00 am to 7:30 am |
使用提出的基于网格搜索的蒙特卡洛仿真方法对两种推出策略下的离港过程进行仿真,为探索不同停机位等待时间阈值对模型的影响,分别将停机位等待时间阈值设定为{15, 20, 25, 30, 35} min,两种策略仿真最优结果如表 2所示。
| 表 2 不同停机位等待时间阈值下两种策略仿真结果 Table 2 Simulation results of two pushback strategies on each gate-hold time threshold |
由表 2的仿真结果可以看出,离港成本随着停机位等待时间阈值的增大而减小,直到Gmax值为30 min时达到最优,继续增加Gmax值对离港成本没有任何影响。在为30 min时,得到2种策略的最优形式分别为
| $ {\rm{SPC:}}{{\lambda '}_{\rm{2}}} = \left\{ \begin{array}{l} \lambda \;\;\;\;\;\;\;n \le 4\\ 0.4\lambda \;\;\;4 < n \le 8\\ 0.2\lambda \;\;\;8 < n \le 14\\ 0\;\;\;\;\;\;\;\;n > 14 \end{array} \right. $ |
| $ {\rm{NPC:}}{{\lambda '}_3} = \left\{ {\begin{array}{*{20}{c}} {\lambda \left[ {1 - \left( {\frac{n}{{0.44N}}} \right)} \right]}&{n < 11}\\ 0&{n \ge 11} \end{array}} \right. $ |
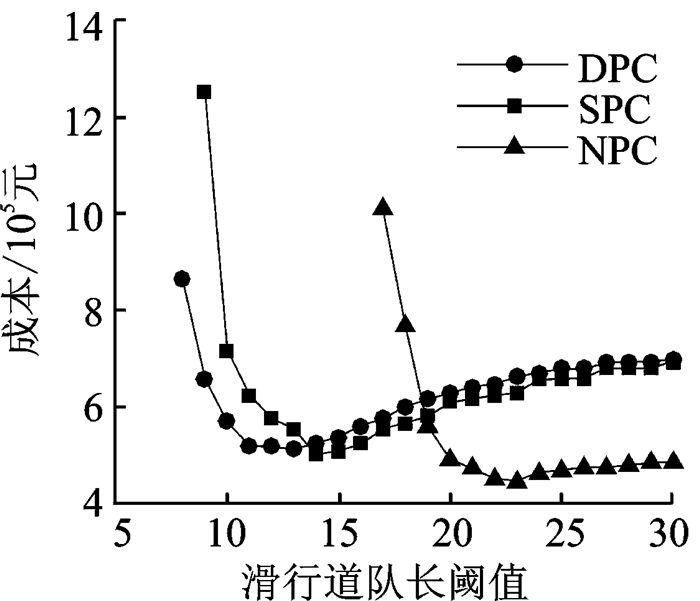
两种策略的各参数确定以后,仿真得到各滑行道队长阈值下的最优成本如图 3所示。
|
图 3 各推出策略成本随N值变化曲线 Figure 3 Effect of total cost of each pushback strategy on N values |
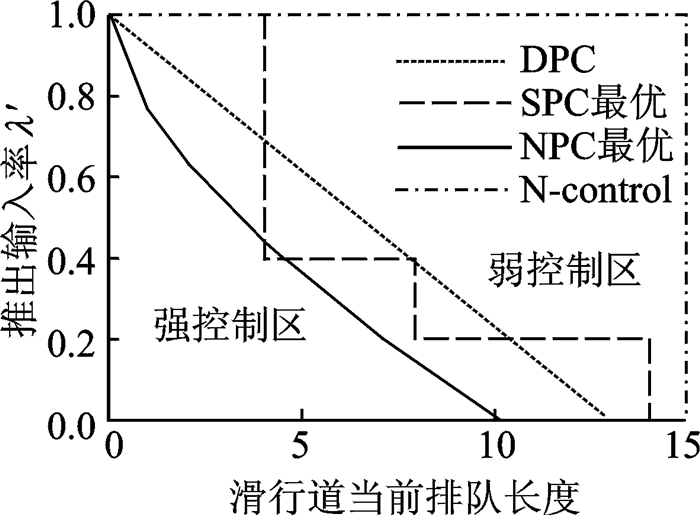
图 3同时给出了DPC策略的成本变化曲线,当队长阈值较小时,由于成本过大在图 3中并未显示出。可以看出,DPC策略、SPC策略和NPC策略取得最优成本时,对应的N值分别为13,14和23。其中SPC策略的最优成本稍好于DPC策略,而NPC策略的最优成本则明显优于DPC策略。图 4描述了包括N-control策略等4种策略在最优情形下的控制函数曲线。
|
图 4 N-control,DPC策略,SPC策略和NPC策略曲线 Figure 4 Curves of N-control, DPC, SPC and NPC strategies |
图 4根据推出策略曲线的位置分布将控制区域分为“弱控制区”和“强控制区”两部分,而图中SPC和NPC最优曲线分别是SPC策略和NPC策略的强弱控制区分界线(以N-control控制策略为最弱强度控制策略)。当策略的曲线自弱控制区向强控制区移动时,离港成本逐渐下降,当曲线越过各自策略的分界线(策略最优)时,离港成本开始逐渐增加(控制强度增加导致停机位等待惩罚逐渐升高)。
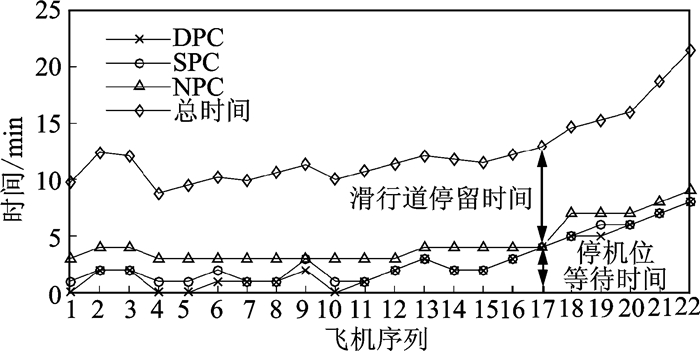
图 5描述了在7:00 am至7:30 am时使用DPC策略,SPC策略和NPC策略时的各航班停机位等待时间和滑行道排队时间细节。
|
图 5 离港高峰期DPC,SPC和NPC策略下的停机位等待时间与滑行道停留时间分配 Figure 5 Time assignment of gate-hold and sojourn on taxiway for DPC, SPC and NPC strategies at departure peak hours |
由于推出策略控制的是两者的时间分配,所以3种推出控制策略控制下的各航班滑行总时长并未变化。图 5中,总时间曲线为停机位等待时间和滑行道停留时间之和,各策略曲线以下为停机位等待时间,策略曲线以上至总时间曲线之间为滑行道停留时间。例如飞机6,在7:10进行申请飞机推出,在3种推出策略控制下,其停机位等待时间和滑行道停留时间分别为1 min和9.2 min,2 min和8.2 min,3 min和7.2 min。可以看出,DPC策略,SPC策略和NPC策略对停机位等待控制效果逐渐增强,对应的滑行道停留时间则会逐渐减少,以达到降低离港成本的效果。
3.2 控制策略对比为了更直观地观察参数对策略的影响程度,使用相同的机场运行数据,分别对无控制,DPC,SPC和NPC策略进行仿真,对比结果如表 3所示。
| 表 3 推出策略最优仿真结果对比 Table 3 Comparison of optimal simulation results for each pushback control strategy |
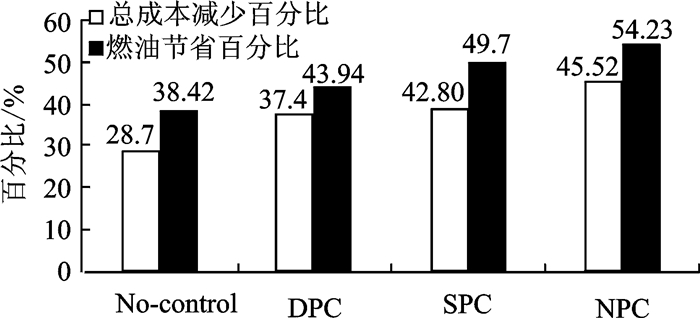
表 3中,VF为燃油消耗量,RT为燃油节省量,在没有任何控制策略时,离港总成本为819 008.3元,燃油消耗量为122 165.5 kg,平均滑行时间为13.70 min;SPC策略最优滑行道排队阈值为14,其总成本和燃油消耗量分别为499 725.3元和61 524.0 kg,虽然总成本比DPC策略有少量降低,但是燃油消耗量具有明显降低;NPC策略最优滑行道排队阈值为23,虽然此阈值较大,但由于线性参数τ的存在,其有效阈值为23×0.44=10.12≈10,NPC策略总成本和燃油消耗量分别为446 168.4元和55 992.8 kg,相对DPC策略都具有更优的成本。它将更多的滑行道等待时间转化为了停机位等待时间。为了更明显地对比各策略优化效果,总成本和燃油节省百分比如图 6所示。
|
图 6 总成本和燃油节省百分比 Figure 6 Saving percentages of total cost and fuel burn consumption |
图 6除了提出的SPC和NPC两种动态推出控制策略外,还给出了当前已有的静态N-control策略和动态DPC策略的总成本及燃油节省成本对比结果。可以看出动态推出控制策略的结果整体优于静态推出策略,而NPC策略的在最优阈值时(N=23)总成本和燃油成本节省分别可达45.52%以及54.23%,可以进一步降低机场的离港成本。虽然SPC策略的成本节省量不是最优的,但是其控制方法在一定区间内为恒定值,具有最简介的控制手段,可以大大降低机场调度者的工作负担。
4 结束语针对当前机场离港地面运行高成本和长时间滑行等待的现状,提出了两种动态推出控制策略的一般形式,使得推出率可以随当前滑行道排队长度实时变化。为了寻找策略的最优参数和滑行道队长阈值的最优值,建立了离港控制模型,并设计了基于网格参数优化的蒙特卡洛仿真优化方法。分别对已有的DPC控制策略和提出的阶梯函数控制策略以及非线性函数控制策略的最优解进行离港过程仿真。仿真对比结果表明,最优参数和队长阈值的合理选择可以使离港推出控制策略具有更好的控制效果。其中NPC策略能够使离港总成本和燃油成本减少45.52%和54.23%;而SPC策略具有减少调度员工作负担的优点,可以为机场管理者调度方式的改进提供建议。
由于未考虑飞机类型的不同,本研究采用平均当量跑道服务时间及滑行燃油成本进行仿真,而且18L/36R跑道为主起飞跑道,此研究并未考虑少量进港飞机的影响,所以存在一定局限性。因此,如何使离港推出策略更具普适性还有待深入研究。
| [1] |
KHADILKAR H, BALAKRISHNAN H.
Estimation of aircraft taxi fuel burn using flight data recorder archives[J]. Transportation Research Part D:Transport and Environment, 2012, 17(7): 532–537.
DOI:10.1016/j.trd.2012.06.005
|
| [2] |
IDRIS H, CLARKE J P, BHUVA R.
Queuing model for taxi-out time estimation[J]. Air Traffic Control Quarterly, 2002, 10(1): 1–22.
DOI:10.2514/atcq.10.1.1
|
| [3] |
CARR F, EVANS A, CLARKE J P, et al. Modeling and control of airport queuing dynamics under severe flow restrictions[C]//Proceedings of the American Control Conference. Anchorage, USA: [s.n.], 2002. |
| [4] |
MADAS M A, ZOGRAFOS K G.
Airport slot allocation:A time for change[J]. Transport Policy, 2010, 17(4): 274–285.
DOI:10.1016/j.tranpol.2010.02.002
|
| [5] |
VOSSEN T, BALL M.
Slot trading opportunities in collaborative ground delay programs[J]. Transportation Science, 2006, 40(1): 29–43.
|
| [6] |
高强, 严俊, 朱金福.协同决策机制下航空公司时隙分配优化决策[J].交通信息与安全, 2012, 30(1): 30-34.
GAO Qiang, YAN Jun, ZHU Jinfu.Airlines' optimization model of slot allocation through collaborative decision-making mechanism[J]. 2012, 30(1): 30-34. |
| [7] |
LIU Lihua, ZHANG Yaping, LIU Lan, et al.
Congestion pricing for aircraft pushback slot allocation[J]. PLoS One, 2017, 12(1): 1–15.
|
| [8] |
PUJET N, DELCAIRE B, FERON E. Input-output modeling and control of the departure process of congested airports[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. Portland, USA: AIAA, 1999. |
| [9] |
CHENG V H L, SHARMA V, FOYLE D C.
A study of aircraft taxi performance for enhancing airport surface traffic control[J]. IEEE Transactions on Intelligent Transportation Systems, 2001, 2(1): 39–54.
|
| [10] |
ROLING P, VISSER H.
Optimal airport surface traffic planning using mixed integer linear programming[J]. International Journal of Aerospace Engineering, 2008, 8(1): 1–11.
|
| [11] |
FERONE R, HANSMAN R J, ODONI A R, et al. The departure planner: A conceptual discussion[R]. Cambridge: Massachusetts Institute of Technology, 1997. |
| [12] |
SIMAIAKIS I, SANDBERG M, BALAKRISHNAN H.
Dynamic control of airport departures:Algorithm development and field evaluation[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 285–295.
DOI:10.1109/TITS.2013.2278484
|
| [13] |
SIMAIAKIS I, KHADIKAR H, BALAKRISHNAN H, et al.
Demonstration of reduced airport congestion through pushback rate control[J]. Transportation Research Part A:Policy and Practice, 2014, 66: 251–267.
DOI:10.1016/j.tra.2014.05.014
|
| [14] |
MARTINEZ H F, BALAKRISHNAN H. Analysis of potential implementations of pushback rate control at LaGuardia airport[C]//Proceedings of the Transportation Research Board 94th Annual Meeting. Washington DC, USA: [s.n.], 2015. |
| [15] |
张亚平, 廉冠, 邢志伟, 等.
飞机推出控制停机位等待惩罚策略[J]. 哈尔滨工业大学学报, 2018, 50(3): 15–21.
ZHANG Yaping, LIAN Guan, XING Zhiwei, et al. Aircraft departure pushback control strategy based on gate-hold penalty[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 15–21. |
| [16] |
中国民航局. 2016年民航行业发展统计公报[R/OL]. (2017-05-08)[2017-09-10]. http://www.caac.gov.cn/XXGK/XXGK/TZTG/201705/P020170508503230814473.pdf.
Civil Aviation Administration of China. 2016 civil aviation industry development statistics bulletin[R/OL]. (2017-05-08)[2017-09-10]. http://www.caac.gov.cn/XXGK/XXGK/TZTG/201705/P020170508503230814473.pdf. |
 2018, Vol. 50
2018, Vol. 50


