在动态系统不确定性分析与设计的研究领域,系统安全性重要性测度分析是一项重点研究内容。重要性测度分析也称为全局灵敏度分析[1],实质上就是不确定性的逆向分配过程,主要任务是确定输出响应量对输入变量不确定性的敏感程度,然后对输入变量的重要性进行排序,其最终目的是为系统设计与优化、以及系统性能监控与维护等提供技术指导。目前,很多学者对重要性测度和及其求解方法进行了研究,并取得了大量研究成果。概括起来,这些重要性测度分析方法主要包括3类:即非参数方法[2]、方差指标[3]和矩独立指标[1],其中方差指标和矩独立指标由于综合考虑了输入变量的不确定性对输出响应量不确定性的平均影响而得到广泛应用。
在传统的系统安全性分析与设计过程中,系统底层元器件的失效率常常作为一个确定值来处理,很少考虑各种不确定性因素的影响。然而,在实际工程中,不确定性具有一定的普遍存性。文献[4, 5]将这些不确定性分为随机不确定性和认知不确定性。Baraldi等[6]认为,由于受内部和外界环境、试验数据和人的认知水平等不确定性因素的影响,元器件的失效率也具有一定的不确定性,因此采用概率函数描述其不确定性更符合工程实际[7, 8]。一般情况下,假定元器件失效率的取值规律服从正态分布[7]、三角分布[7]和对数正态分布函数[8]等。在系统元器件失效率为随机变量的条件下,由于装备的各个系统是由多个元器件组成的一个有机整体,元器件的失效率会直接影响到系统的失效概率,使得系统失效概率也具有随机不确定性的特点。
在不确定性重要性测度分析方面,前期工作主要以结构机构为研究对象,而很少对动态系统进行研究。基于动态系统失效概率的重要性测度是以动态系统失效概率作为响应量,用来度量系统元器件不确定性对系统失效概率的影响程度。虽然文献[9]对动态系统失效概率的重要性测度进行了研究,提出了基于动态系统失效概率的方差重要性测度及其高效算法,但这一指标仅从输出响应量的方差的角度衡量元器件失效率不确定性的贡献程度,存在很大的信息的遗失问题。因此,有必要对这一问题做进一步研究。
本文依据矩独立重要性测度分析的基本思想,根据动态系统失效概率的分布函数(Cumulative distribution function,CDF)能够提取其完整不确定性信息这一特点,分别提出了两种新的矩独立重要性测度,有效解决了系统工作时间给定和在区间变化两种情况下元器件失效率的不确定重要性侧重分析问题。虽然这两种新的重要性测度可以通过蒙特卡罗数值仿真(Monte Carlo simulation, MCS)进行求解,但面临计算成本过高的难题。为此,本文将稀疏网格积分(Sparse grid integration, SGI)技术和Edgeworth级数(Edgeworth series, ES)相结合,提出了重要性测度的高效算法,极大地提高了它们的求解效率。
1 动态系统失效概率的特点分析对于由n个元器件组成的动态系统,假设这些元器件的失效率为λ=[λ1, λ2, …, λn],其中λi为第i个元器件的失效率。由于元器件的失效概率一般为工作时间和其失效率的函数,且服从指数分布。因此, 第i个元器件的失效概率可通过式(1)来表达
| $ P_f^i\left( {t,{\lambda _i}} \right) = 1 - {{\rm{e}}^{ - {\lambda _i}t}} $ | (1) |
由于系统是由多个元器件按照一定结构关系组成的一个有机整体,所以它的失效概率也应该是元器件工作时间t和其失效率λ的函数。假设系统失效概率的表达式为
| $ {P_f} = G\left( {t,\mathit{\boldsymbol{\lambda }}} \right) $ | (2) |
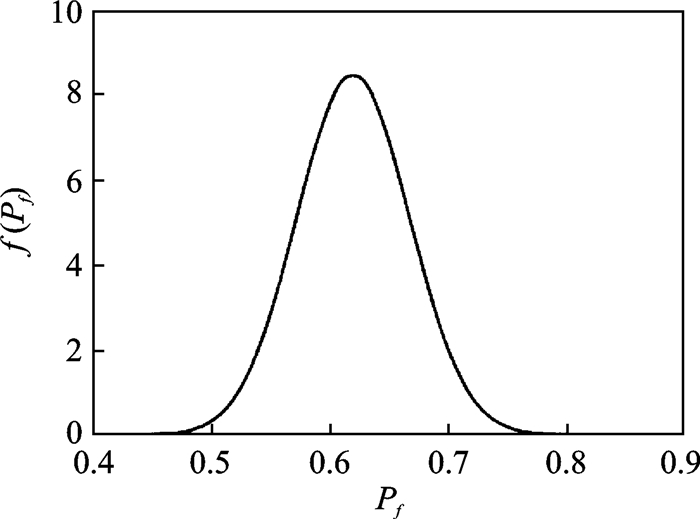
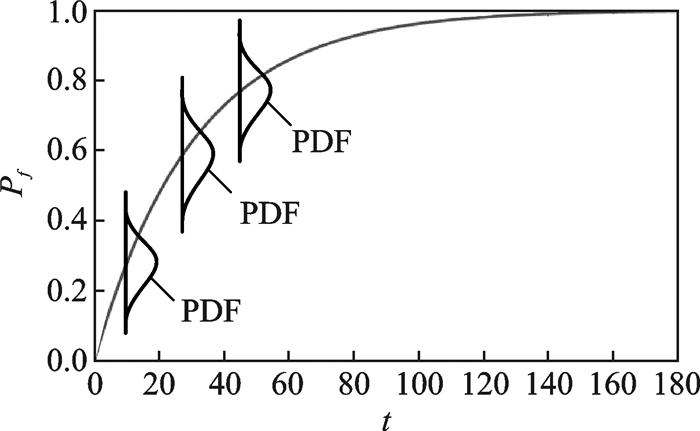
考虑各种不确定性因素的影响,假设式(2)中元器件的失效率λ为服从某联合概率密度函数(Probability density function, PDF)的随机变量。在这种情况下,当系统工作时间t0给定时,元器件失效率λ的不确定性经式(2)传递到输出响应量Pf,使得系统失效概率Pf为服从某PDF的随机变量;当系统工作时间t变化时,系统失效概率Pf所服从的PDF则会随着工作时间t的变化而变化,即系统失效概率Pf为一个动态随机变量。图 1为工作时间为t0时某系统失效概率Pf的概率密度函数f(Pf)示意图,图 2为系统工作时间t变化时某系统失效概率Pf的PDF随时间的变化示意图。
|
图 1 系统工作时间给定时系统失效概率的PDF曲线 Figure 1 PDF curve of system failure probability in a fixed function time |
|
图 2 系统工作时间变化时系统失效概率的变化曲线 Figure 2 Curve of system failure probability with function time changing |
2 基于动态系统系统失效概率的矩独立重要性测度
为了分析不确定性元器件失效率对系统失效概率的影响,依据Borgonovo的矩独立灵敏度分析思想,本节分别建立了系统工作时间给定和在区间变化两种情况下的矩独立重要性测度。
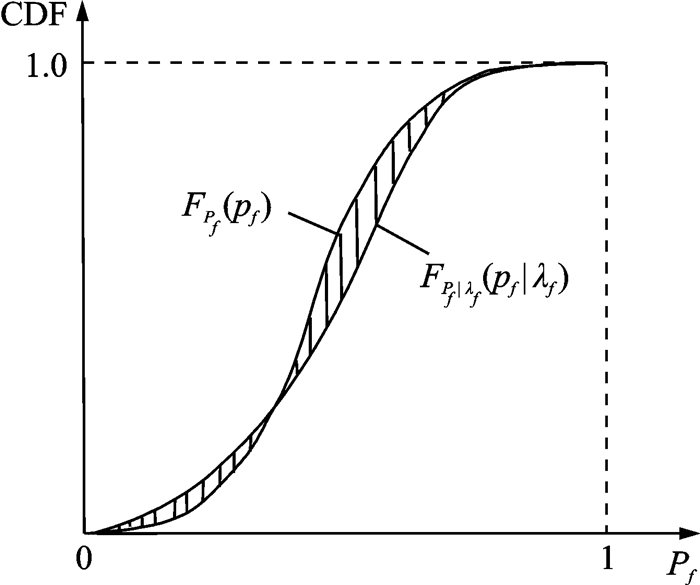
2.1 系统工作时间给定时矩独立重要性测度对于由式(2)表达的动态系统失效概率函数,设f(λ)为元器件失效率λ的联合PDF,fi(λi)为第i个元器件失效率λi的PDF。在系统工作时间为t0时,依据元器件失效率λ的联合概率密度函数f(λ),通过式(2)可得到系统失效概率Pf的无条件分布函数CDF, 记为FPf(pf);当按照元器件失效率λi的概率密度函数fi(λi)取任意实现值λi*时,由于元器件失效率λi取值的固定而使得其不确定性消失,从而导致系统失效概率Pf的取值规律发生相应的变化,这种情况依据元器件失效率λ~i(除λi之外其他元器件的失效率组合)的联合PDF f(λ~i),可得到系统条件失效概率的CDF, 记为FPf|λi(pf|λi)。因此,FPf(pf)与FPf|λi(pf|λi)之间的差异,表征了失效率λi取实现值λi*时元器件失效率λi的不确定性对系统失效概率Pf的CDF的影响程度。图 3给出了FPf(pf)曲线与FPf|λi(pf|λi)曲线的不同。两个CDF之间的差异可由式(3)所表达的积分值A(λi)来计算,A(λi)的几何示意为图 3中阴影部分的面积。
|
图 3 系统失效概率的无条件和条件CDF曲线 Figure 3 Unconditional and conditional CDFs Curves of system failure probability |
| $ A\left( {{\lambda _i}} \right) = \int_0^1 {\left| {{F_{{P_f}}}\left( {{P_f}} \right) - {F_{{P_f}\left| {{\lambda _i}} \right.}}\left( {{P_f}\left| {{\lambda _i}} \right.} \right)} \right|{\rm{d}}{p_f}} $ | (3) |
由于λi为随机变量,其取值规律由其概率密度函数fi(λi)确定,当λi按照fi(λi)取所有可能实现值时,A(λi)的平均值为
| $ {E_{{\lambda _i}}}\left( {A\left( {{\lambda _i}} \right)} \right) = \int {{f_i}\left( {{\lambda _i}} \right)A\left( {{\lambda _i}} \right){\rm{d}}{\lambda _i}} $ | (4) |
Eλi(A(λi))反映了元器件失效率λi的不确定性对系统失效概率Pf分布函数平均影响;由式(3)和式(4)可知,Eλi(A(λi))的量纲由A(λi)的量纲决定,而A(λi)的量纲取决于系统失效概率Pf的量纲。因此,为了消除量纲的影响,本文将式(5)定义为系统工作时间给定时动态系统元器件失效率的矩独立重要性测度,记为SλiCDF
| $ S_{{\lambda _i}}^{{\rm{CDF}}} = \frac{{{E_{{\lambda _i}}}\left( {A\left( {{\lambda _i}} \right)} \right)}}{{E\left( {{P_f}} \right)}} $ | (5) |
由于系统失效概率Pf及其和条件分布函数FPf|λi(pf|λi)均介于0和1之间,所以式(3)和式(4)所表示的A(λi)和Eλi(A(λi))均为介于0和1之间。又由于系统失效概率Pf数学期望E(Pf)也是介于0和1之间的数,所以式(5)所表示重要性测度SλiCDF为没有量纲的非负数。由重要性测度SλiCDF的定义可知,元器件失效率对应的SλiCDF越大,说明该元器件失效率的不确定性对系统失效概率Pf不确定性的影响越大,反之亦然。因此,通过元器件失效率对应的SλiCDF的大小,可以用来对动态系统元器件失效率的重要性进行分析。
由式(4), (5)可以看出,本文所提的矩独立重要性测度反映了元器件失效率的不确定性对系统失效概率分布函数平均影响。由于分布函数反应了随机变量的完整不确定性信息,而方差仅反应了随机变量偏离其均值的程度,因此在系统工作时间给定的情况下,分析元器件失效率的不确定性对系统失效概率不确定性的影响程度时,文献[9]所提的方差重要性测度比本文所提的矩独立重要性测度考虑的不确定性信息更加完善和全面。
2.2 系统时间在区间变化时矩独立重要性测度当系统工作时间在[t1, t2]内变化时,系统元器件失效率的矩独立重要性测度SλiCDF则为工作时间t的单变量函数,这种情况下元器件失效率λi的不确定性对系统失效概率的CDF的影响,可通过SλiCDF在区间[t1, t2]上的积分值B(λi, t)来衡量
| $ B\left( {{\lambda _i},t} \right) = \int_{{t_1}}^{{t_2}} {S_{{\lambda _i}}^{{\rm{CDF}}}{\rm{d}}t} $ | (6) |
为了消除量纲的影响,系统工作时间在区间[t1, t2]内变化时,系统元器件失效率的矩独立重要性测度定义为
| $ S_{{\lambda _i}}^{{t_1}{t_2}} = \frac{{B\left( {{\lambda _i},t} \right)}}{{{t_2} - {t_1}}} $ | (7) |
由式(6)和式(7)可知,Sλit1t2反应了动态系统在一定时间区间变化时元器件失效率λi不确定性对系统失效概率CDF的平均影响。同理,元器件失效率对应的Sλit1t2越大,则表明系统工作时间在区间[t1, t2]内变化时,该元器件失效率的不确定性对系统失效概率不确定性的影响也就越大。
3 基于动态系统系统失效概率的矩独立重要性测度的求解 3.1 Monte Carlo数字模拟法依据大数定理,运用MCS方法,下面给出前面所提两种重要性测度的一般求解方法及步骤。
3.1.1 系统工作时间给定时矩独立重要性测度的求解步骤步骤1 估算动态系统失效概率Pf的无条件分布函数FPf(pf)。给定系统工作时间t0,根据元器件失效率λ的联合概率密度函数f(λ),生成N组样本λk=(λk1, λk2, …, λkn)T(k=1, …, N),将其代入系统失效概率函数Pf=G(t, λ),获得N组系统失效概率样本{pf1, pf2, …, pfN};然后估算系统失效概率Pf的数学期望E(Pf)及无条件分布函数FPf(pf)。
步骤2 估算系统失效概率Pf的条件分布函数FPf|λi(pf|λi)。对每一个元器件失效率λi,根据其概率密度函数fi(λi)获取M个样本{λi1, λi2, …, λiM};分别将元器件失效率λi固定在λik(k=1, 2, …, M)处,再根据输入变量λ~i的联合概率密度函数f(λ~i),生成N组样本,代入系统失效概率函数Pf=G{t, λ},求解对应的系统条件失效概率Pf|λi,进而估算对应的条件分布函数FPf|λi(pf|λi)。
步骤3 计算重要性测度SλiCDF。根据前面所求的系统失效概率Pf的FPf(pf), FPf|λi(pf|λi)和E(Pf),求解重要性测度SλiCDF。
3.1.2 系统工作时间在区间变化时重要性测度的求解步骤步骤1 离散系统工作时间区间。在系统工作时间区间[t1, t2]内,将工作时间t离散成NI个时间点{t1, t2, …, tNI}。
步骤2 求解各时间点对应的重要性测度。对于每个时间tk(k=1, 2, …, NI), 按照3.1.1节给出的重要性测度SλiCDF求解步骤,求解对应的重要性测度SλiCDF(tk)。
步骤3 计算重要性测度Sλit1t2。根据前面所求各时间的SλiCDF(tk)(k=1, 2, …, NI),通过式(8)求解重要性测度Sλit1t2
| $ S_{{\lambda _i}}^{{t_1}{t_2}} = \frac{{\sum\limits_{k = 2}^{{N_I}} {\left( {{t_k} - {t_{k - 1}}} \right)\left( {S_{{\lambda _i}}^{{\rm{CDF}}}\left( {{t_{k - 1}}} \right) + S_{{\lambda _i}}^{{\rm{CDF}}}\left( {{t_k}} \right)} \right.} }}{{2\left( {{t_2} - {t_1}} \right)}} $ | (8) |
要提高本文所提出的两个重要性测度求解效率,关键是要提高式(5)所表达的重要性测度求解效率。为此,本节将SGI技术和ES方法相结合,建立了基于动态系统失效概率的重要性测度的高效算法。下面给出所提算法的基本原理。
3.2.1 稀疏网格积分方法稀疏网格积分方法[10]建立在Smolyak准则的基础之上,它的基本思想是将多元函数的积分问题转化成一元函数积分的张量积组合。
设U1ij和w1ij为第j个变量在一维空间中的积分点和权重,它们可通过单变量条件下的高斯积分、Clenshaw-Curits或梯形准则等方法获得[11]。在k精度水平下,n维空间中所有的SGI点集合Unk可由以下Smolyak准则选取[10]
| $ \mathit{\boldsymbol{U}}_n^k = \bigcup\limits_{k + 1 \le \left| i \right| \le q} {U_1^{{i_1}} \otimes U_1^{{i_2}} \otimes \cdots \otimes U_1^{{i_n}}} $ | (9) |
式中:⊗表示张量积运算符,q=k+n,|i|=i1+…+in为多维指标之和,在Unk中的第j个积分点ξj=(ξji1i1, …, ξjinin)∈Unk的权重wj可由式(10)来确定
| $ {w_j} = {\left( { - 1} \right)^{q - \left| i \right|}}\left( \begin{array}{l} n - 1\\ q - \left| i \right| \end{array} \right)\left( {w_{{j_{{i_1}}}}^{{i_1}} \cdots w_{{j_{{i_n}}}}^{{i_n}}} \right) $ | (10) |
对于非线性函数g(X),它的输入变量为X=(X1, X2, …, Xn),n表示输入变量的维数。则非线性函数g(X)的积分可由式(11)所示的SGI公式求解,其计算精度能够达到2k+1阶多项式的精度[12]
| $ \int {g\left( \mathit{\boldsymbol{X}} \right){f_\mathit{\boldsymbol{X}}}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \approx \sum\limits_{l = 1}^{N_n^k} {{w_l}g\left( {{\mathit{\boldsymbol{x}}_l}} \right)} $ | (11) |
式中:fX(x)为输入变量X的联合CDF。wl和ξl∈Unk分别为通过稀疏网格选点技术得到的n维空间中的权重以及相应的积分点,Nnk为积分点的个数。xl表示第l个积分点ξl对应于原始变量空间的输入变量X的实现值。因此,运用式(11)可以求解动态系统失效概率的各阶矩。
基于Smolyak准则的稀疏网格取点技术,依据限制条件k+1≤|i|≤q能够从全网格中剔除大量对提高积分精度贡献小的点,这在很大程度上克服了传统数值积分计算量随变量维数程指数级增长的难题,因而能够有效解决高维积分问题,且实现过程简易灵活。
3.2.2 基于SGI和Edgeworth级数的CDF高效求解算法对于输入变量为X=(X1, X2, …, Xn)的不确定性模型Y=g(X), 其响应量的CDF在y处的值等于响应量Y小于y值的概率,即
| $ {F_Y}\left( y \right) = P\left\{ {Y \le y} \right\} $ | (12) |
在此定义新的功能函数为
| $ Z\left( {\mathit{\boldsymbol{X}},y} \right) = g\left( \mathit{\boldsymbol{X}} \right) - y $ | (13) |
通过式(12)和式(13)可得以下关系式
| $ {F_Y}\left( y \right) = {P_f}\left\{ {Z\left( {\mathit{\boldsymbol{X}},y} \right)} \right\} = P\left\{ {Z\left( {\mathit{\boldsymbol{X}},y} \right) \le 0} \right\} $ | (14) |
式(14)表示响应量分布函数在y处的值等于功能函数Z(X, y)的失效概率。依据基于点估计方法的失效概率求解理论[13],结构系统的失效概率可以通过其功能函数的各阶矩的函数关系来近似表达。由于矩方法不需要求解设计点以及导数,因此具有便于实现和容易收敛等优点。依据结构系统的失效概率的四阶矩估计方法,响应量分布函数在y处的值可以表示为
| $ {F_Y}\left( y \right) = {P_f}\left\{ {Z\left( {\mathit{\boldsymbol{X}},y} \right)} \right\} = {P_{f4M}} $ | (15) |
式中Pf4M为基于Edgeworth级数的功能函数的失效概率[14],其表达式为
| $ \begin{array}{*{20}{c}} {{P_{f4M}} = \mathit{\Phi }\left( { - {\beta _{2M}}} \right) - \mathit{\Phi }\left( { - {\beta _{2M}}} \right)\left[ {\frac{1}{6}{a_{3Z}}{H_2}\left( { - {\beta _{2M}}} \right) + } \right.}\\ {\left. {\frac{1}{{24}}\left( {{a_{4Z}} - 3} \right){H_3}\left( { - {\beta _{2M}}} \right) + \frac{1}{{72}}a_{3Z}^2{H_5}\left( { - {\beta _{2M}}} \right)} \right]} \end{array} $ | (16) |
式中:Φ(·)和φ(·)分别为标准正态分布的CDF和PDF,H2(x)、H3(x)和H5(x)分别为二阶、三阶和五阶Hermit正交多项式,即
| $ \begin{array}{*{20}{c}} {{H_2}\left( x \right) = {x^2} - 1}\\ {{H_3}\left( x \right) = {x^3} - 3x}\\ {{H_5}\left( x \right) = {x^5} - 10{x^3} + 15x} \end{array} $ | (17) |
βSM为结构系统功能函数的二阶矩可靠度指标,有
| $ {\beta _{SM}} = \frac{{{\alpha _{1Z}}}}{{{\alpha _{2Z}}}} $ | (18) |
alZ(l=1, 2, 3, 4)为结构系统功能函数Z(X, y)的前四阶距,根据式(13),Z(X, y)与g(X)的各阶矩之间存在以下关系
| $ \left\{ \begin{array}{l} {\alpha _{1Z}} = {\alpha _{1g}} - y\\ {\alpha _{2Z}} = {\alpha _{2g}}\\ {\alpha _{3Z}} = {\alpha _{3g}}\\ {\alpha _{4Z}} = {\alpha _{4g}} \end{array} \right. $ | (19) |
式中, αlg(l=1, 2, 3, 4)为函数g(X)的前四阶矩。
如果确定了输入变量的CDF,g(X)的矩就不会改变。通过式(19)可知,功能函数Z(X, y)的前四阶矩中,除了它的一阶矩随y的变化而变化,其他矩均没有变化。因此,若能得到函数g(X)的前四阶矩αlg(l=1, 2, 3, 4),就可以建立y与FY(y)之间的显式关系式,记为
| $ {F_Y}\left( y \right) = \theta \left( y \right) $ | (20) |
式中θ(·)表示映射关系。式(20)表明响应量分布函数FY(y)为y的单变量函数。
依据SGI技术,函数g(X)的前四阶矩αlg(l=1, 2, 3, 4)可由以下4个表达式进行估计
| $ {\alpha _{1g}} = \int {g\left( \mathit{\boldsymbol{x}} \right){f_\mathit{\boldsymbol{X}}}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \approx \sum\limits_{l = 1}^P {{w_l}g\left( {{\mathit{\boldsymbol{x}}_l}} \right)} $ | (21) |
| $ \begin{array}{l} {\alpha _{2g}} = {\left[ {\int {{{\left( {g\left( \mathit{\boldsymbol{x}} \right) - {\alpha _{1g}}} \right)}^2}{f_\mathit{\boldsymbol{X}}}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} } \right]^{1/2}} \approx \\ \;\;\;\;\;\;\;\;\;{\left[ {\sum\limits_{l = 1}^P {{w_l}{{\left( {g\left( {{\mathit{\boldsymbol{x}}_l}} \right) - {\alpha _{1g}}} \right)}^2}} } \right]^{1/2}} \end{array} $ | (22) |
| $ \begin{array}{l} {\alpha _{3g}} = \frac{1}{{\alpha _{2g}^3}}\int {{{\left( {g\left( \mathit{\boldsymbol{x}} \right) - {\alpha _{1g}}} \right)}^3}{f_\mathit{\boldsymbol{X}}}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \approx \\ \;\;\;\;\;\;\;\;\frac{1}{{\alpha _{2g}^3}}\sum\limits_{l = 1}^P {{w_l}{{\left( {g\left( {{\mathit{\boldsymbol{x}}_l}} \right) - {\alpha _{1g}}} \right)}^3}} \end{array} $ | (23) |
| $ \begin{array}{l} {\alpha _{4g}} = \frac{1}{{\alpha _{2g}^4}}\int {{{\left( {g\left( \mathit{\boldsymbol{x}} \right) - {\alpha _{1g}}} \right)}^4}{f_\mathit{\boldsymbol{X}}}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \approx \\ \;\;\;\;\;\;\;\;\frac{1}{{\alpha _{2g}^4}}\sum\limits_{l = 1}^P {{w_l}{{\left( {g\left( {{\mathit{\boldsymbol{x}}_l}} \right) - {\alpha _{1g}}} \right)}^4}} \end{array} $ | (24) |
式中的n维积分点xl以及相应的权重wl可以通过SGI方法获得。
由于本文所提的重要性测度的求解是一个嵌套的双层循环过程,需要求解大量的系统失效概率来确定其条件和无条件CDF。在系统底层元器件数目较多的情况下,系统失效概率函数的维度很高,这将导致系统失效概率的时间很长,致使本文所提矩独立重要性测度难以求解。虽然采用Monte Carlo数字模拟法,可以准确地求解系统元器件失效率的矩独立重要性测度,但由于该方法需要大量样本而使得计算成本非常巨大。针对这一问,本文首先将系统失效概率CDF的求解问题转化为式(13)和式(14)所表达的功能函数失效概率的求解,然后采用于Edgeworth级数对该功能函数的失效概率进行估计。由于基于Edgeworth级数的功能函数失效概率的求解仅与功能函数的前四阶矩有关,而采用稀疏网格积分方法可以通过少量系统失效概率就可以求解其前四阶矩,因此将Edgeworth级数和稀疏网格积分方法相结合,在保证计算精度情况下,能够大大降低系统失效概率的求解次数,从而有效提高矩独立重要性测度的计算效率。
3.2.3 高效算法的求解步骤对于第2部分提出的重要性测度SλiCDF,可采用将SGI技术和ES方法相结合的方法,即SGI-ES方法对其进行求解,具体步骤如下:
步骤1 估算系统失效概率的无条件CDF。首选,给定系统工作时间t0,指定稀疏网格精度水平k1;然后,由式(9)和式(10)获得与系统失效概率函数Pf=G(t, λ)所对应的n维元器件失效λ的积分点λl及其权重wl(l=1, 2, …, N);接着,通过式(21)至式(24)计算失效概率Pf的前四阶矩αlG(l=1, 2, 3, 4);最后,通过式(15)至式(19)求解系统失效概率的数学期望E(Pf)和无条件分布函数FPf(pf)。
步骤2 确定元器件失效率λi(i=1, 2, …, n)的积分点及权重。指定稀疏网格精度水平k2,由式(9)和式(10)获得单变量函数对应的λi积分点λij及权重wij(j=1, …, m)。
步骤3 估算系统失效概率的条件CDF。对于元器件失效率λi的每一个积分点λij,指定稀疏网格精度水平k3,根据方法由式(9)和式(10)获得与条件系统失效概率函数Pf|λij=G(t, λ~i)所对应的n-1维的积分点λ~i及其相应的权重w~i(i=1, 2, …, NT);通过式(21)至式(24),求解失效概率Pf|λij的前四阶矩α~lG(l=1, 2, 3, 4);最后通过式(15)至式(19)求解系统失效概率的条件分布函数FPf|λij(pf|λij)(j=1, …, m)。
步骤4 计算重要性测度SλiCDF。根据步骤1至步骤3所求解的FPf(pf),FPf|λij(pf|λij)和E(Pf),通过式(25)和式(26)求解重要性测度SλiCDF
| $ A\left( {\lambda _i^j} \right) = \int {\left| {{F_{{P_f}}}\left( {{P_f}} \right) - {F_{{P_f}\left| {\lambda _i^j} \right.}}\left( {{P_f}\left| {\lambda _i^j} \right.} \right)} \right|{\rm{d}}{p_f}} $ | (25) |
| $ S_{{\lambda _i}}^{{\rm{CDF}}}\left( {{t_0}} \right) = \frac{{{E_{{\lambda _i}}}\left( {A\left( {{\lambda _i}} \right)} \right)}}{{E\left( {{P_f}} \right)}} = \frac{{\sum\limits_{j = 1}^m {w_i^jA\left( {\lambda _i^j} \right)} }}{{E\left( {{P_f}} \right)}} $ | (26) |
为验证所提重要性测度的合理性和SGI-ES算法的高效性,通过两个算例对其进行验证。
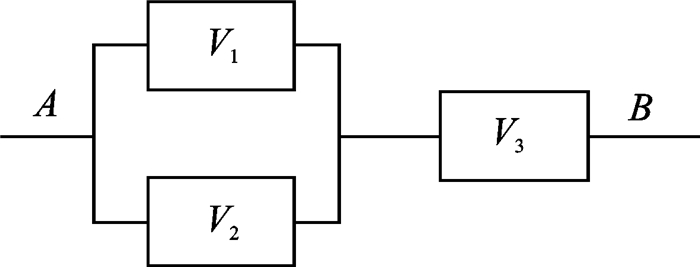
4.1 阀门控制系统图 4为一个由V1, V2和V33个部件组成的阀门控制系统[15],它的主要功能是控制流体从A端到B端时的工作状态。控制系统有正常和失效两种工作状态,正常状态对应于阀门“畅通”状态,失效状态对应于阀门为“断开”状态。这3个部件的失效率为随机变量,其取值规律服从对数正态分布,具体参数见表 1。系统失效概率函数为
| $ {P_f} = {P_{f{\lambda _1}}}{P_{f{\lambda _2}}} + {P_{f{\lambda _3}}} - {P_{f{\lambda _1}}}{P_{f{\lambda _2}}}{P_{f{\lambda _3}}} $ | (27) |
|
图 4 阀门控制系统 Figure 4 Valve control system |
| 表 1 三个元器件失效率的分布参数 Table 1 Distribution parameters of the three components' failure rates |
式中:Pfλ1, Pfλ2和Pfλ3分别为部件1、部件2和部件3的失效概率。
下面运用基于系统失效概率的矩独立重要性测度,采用MCS和SGI-ES两种算法,对阀门控制系统元器件失效率的重要性进行分析。
(1) 在工作时间为t0=30时,分别运用文献[9]所提的方差重要性测度SλiPf和本文所提的矩独立重要性测度SλiCDF对阀门控制系统元器件失效率λi(i=1, 2, 3)的重要性进行分析,其中矩独立重要性测度SλiCDF分别采用MCS和SGI-ES两种算法求解。表 2列出了两种重要性测度的计算结果和采用MCS和SGI-ES两种算法求解矩独立重要性测度SλiCDF时调用功能函数的次数。
| 表 2 工作时间给定时元器件失效率的重要性测度 Table 2 Importance measures of components'failure rates in a fixed function time |
(2) 工作时间t∈[20, 50]的情况下,运用SGI-ES方法求解阀门控制系统元器件失效率λi(i=1, 2, 3)的矩独立重要性测度Sλit1t2,计算结果如表 3所示。
| 表 3 工作时间在区间变化时的元器件失效率重要性测度 Table 3 Importance measures of components'failure rates in an interval variant working time |
由表 2可以看出,在系统工作时间为30时,文献[9]所提的方差重要性测度和本文提出的矩独立重要性测度给出的阀门控制系统3个元器件重要性排序皆为λ3>λ2>λ1。这一结果表明:无论是文献[9]所提的方差重要性测度,还是本文所提的矩独立重要性测度,都能够有效地对动态系统元器件失效率的重要性进行分析。但是,这两种重要性测度在对系统元器件失效率的重要性程度进行分析时关注点不同,文献[9]所提的方差重要性测度主要关注元器件失效率的不确定性对系统失效概率的方差(局部不确定性)的影响程度,而本文提出的矩独立重要性测度则关注元器件失效率的不确定性对系统失效概率的分布函数(完整不确定性)的影响程度。
由表 2和表 3计算结果可以看出,无论系统工作时间为30时,还是在区间[20, 50]内变化,本文提出的矩独立重要性测度给出的阀门控制系统3个元器件重要性排序皆为λ3>λ2>λ1。这一结果表明本文所提的两种基于系统失效概率的矩独立重要性测度,都能够有效地对动态系统元器件失效率的重要性测度进行分析,从而验证本文所提指标的可行性。
从表 2所列的功能函数调用次数来看,通过两种算法得到的阀门控制系统3个元器件失效率的矩独立重要性测度值基本一致,且在满足精度要求的前提下,SGI-ES方法调用功能函数的次数远远小于MCS方法,这表明本文所提的SGI-ES算法比MCS方法更加高效。
由表 2和表 3计算结果还可以看,从无论系统工作时间为30时,还是在区间[20, 50]内变化,3种重要性分析结果一致认为对阀门控制系统的失效概率影响最大的部件是元器件V3,影响最小的部件是元器件V1,因此在实际工作中,要想保证阀门控制系统稳健正常地运行,应重点加强对元器件V3的检测、维修和保养。
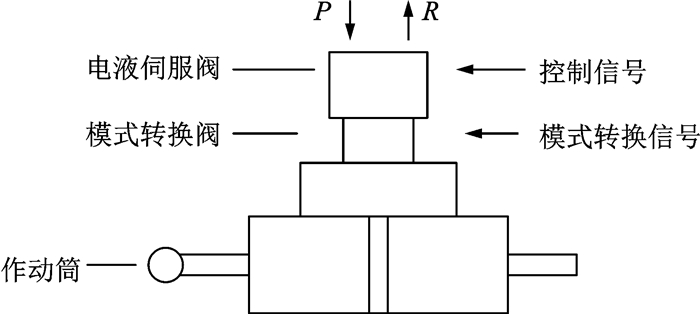
4.2 民用飞机电液舵机系统以文献[15]研究的空客A系列飞机舵面电液舵机系统为对象,它的主控制舵机的结构示意图如图 5所示。通过对空客A系列飞机舵面电液舵机系统的功能危险分析,得到“舵机不动作”这一失效模式对飞机的安全运行具有重大影响,因此需要对其进行重点分析。
|
图 5 空客A系列飞机电液舵机系统的结构示意图 Figure 5 Aircraft electro-hydraulic actuator structure of the inairbus A |
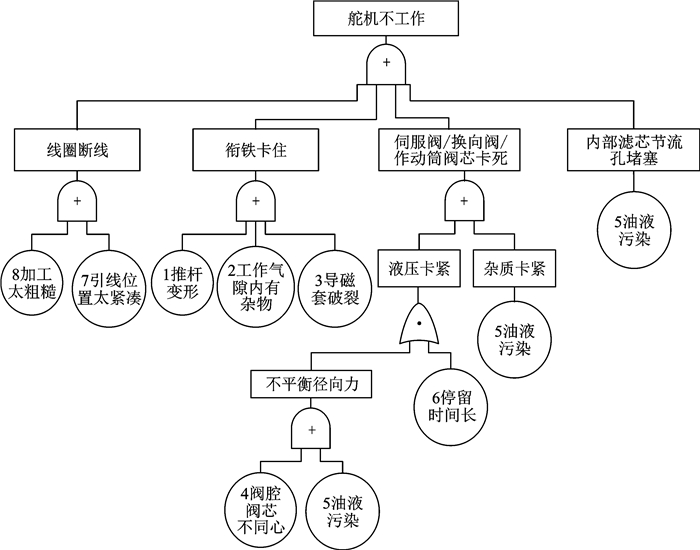
依据该客机舵面电液舵机系统的结构组成、工作原理和经验数据,以失效模式“舵机不动作”为故障树的顶事件,构建如图 6所示的电液舵机系统故障树。
|
图 6 飞机电液舵机系统故障树 Figure 6 Fault tree of aircraft electro-hydraulic actuator system |
通过故障树可得到系统失效概率的表达式Pf(t, λ),λi(i=1, 2, …, 8)为故障树中8个底事件的失效率。其中:1表示“推杆变形”,2表示“工作气隙内有杂物”,3表示“导瓷套破裂”,4表示“阀腔阀芯不同心”,5表示“油液污染”,6表示“停留时间长”,7表示“引线位置太紧促”,8表示“加工太粗糙”。故障树底事件的取值规律皆为服从对数正态分布随机变量,具体数据见表 4。
| 表 4 8个底事件的失效率分布参数 Table 4 Distribution parameters of the eight basic events'failure rates |
运用基于系统失效概率的矩独立重要性测度,采用MCS和SGI-ES两种算法,对该飞机舵面电液舵机系统元器件失效率的重要性进行分析。
(1) 系统工作时间t0=5 000时,同理分别求解飞机舵面电液舵机系统元器件失效率λi(i=1, 2, …, 8)的重要性测度SλiPf和SλiCDF,以及采用MCS和SGI-ES两种算法求解SλiCDF时调用功能函数的次数,结果见表 5。
| 表 5 工作时间给定时底事件失效率重要性测度 Table 5 Importance measures of basic events' failure rates in a fixed function time |
(2) 在工作时间为[3 500, 6 500]情况下,运用SGI-ES方法求解飞机舵面电液舵机系统元器件失效率λi(i=1, 2, …, 8)的矩独立重要性测度值,结果如表 6所示。
| 表 6 工作时间在区间变化时底事件失效率重要性测度 Table 6 Importance measures of basic events' failure rates in an interval variant working time |
由表 5可以看出,在系统工作时间为5 000时,文献[9]所提的方差重要性测度给出的飞机舵面电液舵机系统8个元器件的重要性排序为λ5>λ8>λ7>λ2>λ3>λ1>λ4=λ6,而本文提出的矩独立重要性测度给出的排序为λ5>λ1>λ3>λ2>λ7>λ8>λ6>λ4。虽然两种重要性测度所给出的排序不完全一致,但它们一致认为λ5对飞机舵面电液舵机系统失效概率的不确定性影响最大,λ4和λ6对飞机舵面电液舵机系统失效概率的不确定性影响最小。这一结果表明从不同的角度衡量系统元器件失效率的重要性程度,所得到的结果并不完全相同,这是由于文献[9]所提的方差重要性测度主要关注元器件失效率的不确定性对系统失效概率的方差(局部不确定性)的影响程度,而本文提出的矩独立重要性测度则关注元器件失效率的不确定性对系统失效概率的分布函数(完体不确定性)的影响程度。由此可见,这两种重要性测度之间不可能相互代替。在实际工程中,针对具体问题,应结合相应的工程要求和设计人员的关注对象,选择合理的重要性测度结果指导工程设计。
由表 5和表 6计算结果可以看出,无论系统工作时间为5 000时,还是在区间[3 500, 6 500]内变化,本文提出的矩独立重要性测度,所给出的飞机舵面电液舵机系统8个元器件的重要性排序结果完全相同,均为λ5>λ1>λ3>λ2>λ7>λ8>λ6>λ4。这一结果表明本文所提的两种基于系统失效概率的矩独立重要性测度,都能够有效地对动态系统元器件失效率的重要性测度进行分析,从而再次验证了本文所提指标的可行性。
从表 5所列的功能函数调用次数来看,通过两种算法得到的飞机舵面电液舵机系统的8个元器件失效率的矩独立重要性测度值基本一致,且在满足精度要求的前提下,SGI-ES方法调用功能函数的次数远远小于MCS方法,这一结果也再次表明本文所提的SGI-ES算法比MCS方法更加高效。
由表 5和表 6的计算结果还可以看出,无论系统工作时间为5 000时,还是在区间[3 500, 6 500]内变化,3种重要性分析结果一致认为油液污染(λ5)因素对系统失效概率的影响最大,而阀腔阀芯不同心(λ4)和停留时间长(λ6)这两个因素对系统失效概率几乎没影响。因此,为了预防因飞机舵面电液舵机系统失效而导致不安全事件的发生,在实际维护工作中,应经常检测油液的污染情况,及时清理油液系统,防止油液污染。
5 结束语鉴于动态系统失效概率分析在安全工程中的重要地位,文章研究了不确定因素影响下系统元器件失效率的重要性测度分析问题。
(1) 分析了动态系统失效概率的特点。在实际工程中,受各种不确定性因素的影响,动态系统元器件的失效率具有一定的不确定性。当系统元器件的失效率采用概率分布函数描述时,动态系统的失效概率则为元器件失效率和系统工作时间的多变量随机函数。当系统工作时间变化时,系统失效概率分布函数则随着时间变化而发生变化。
(2) 提出了两种新的基于系统失效概率的矩独立重要性测度, 解决了系统工作时间给定和在区间变化两种情况下元器件失效率不确定对动态系统失效概率影响程度的度量问题,为动态系统元器件失概率重要性测度分析提供一种可供选的方法。
(3) 提出了一种高效的重要性测度求解算法。将SGI技术和ES方法相结,解决系统失效概率分布函数的求解问题,有效降低了功能函数调用次数,显著地提高了重要性测度的求解效率。算例分析结果表明,本文提出重要性测度及其高效算法可行有效。
| [1] |
BORGONOVO E.
A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771–784.
|
| [2] |
SALTELLI A, MARIVOET J.
Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28(2): 229–253.
|
| [3] |
SOBOL I M.
Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1): 271–280.
|
| [4] |
XU M, CHEN T, YANG X H.
The effect of parameter uncertainty on achieved safety integrity of safety system[J]. Reliability Engineering & System Safety, 2012, 99: 15–23.
|
| [5] |
TANG Z C, ZUO M J, XIAO N C.
An efficient method for evaluating the effect of input parameters on the integrity of safety systems[J]. Reliability Engineering & System Safety, 2016, 145: 111–123.
|
| [6] |
BARALDI P, ZIO E, COMPARE M.
A method for ranking components importance in presence of epistemic uncertainties[J]. Journal of Loss Prevention in the Process Industries, 2009, 22(5): 582–592.
DOI:10.1016/j.jlp.2009.02.013
|
| [7] |
ZAFIROPOULOS E P, DIALYNAS E N.
Reliability and cost optimization of electronic devices considering the component failure rate uncertainty[J]. Reliability Engineering & System Safety, 2004, 84(3): 271–284.
|
| [8] |
BLANKS H S.
Arrhenius and the temperature dependence of non-constant failure rate[J]. Quality and Reliability Engineering International, 1990, 6(4): 259–265.
|
| [9] |
巩祥瑞, 吕震宙, 刘辉, 等.
动态系统失效的不确定性分析及高效算法[J]. 北京航空航天大学学报, 2017, 43(7): 1460–1469.
GONG Xiangrui, LV Zhenzhou, LIU Hui, et al. Uncertainty analysis of failure in dynamic system and its efficient solution[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7): 1460–1469. |
| [10] |
SMOLYAK S A.
Quadrature and interpolation formulas for tensor products of certain classes of functions[J]. Soviet Mathematics Doklady, 1963, 4: 240–243.
|
| [11] |
GERSTNER T, GRIEBEL M.
Numerical integration using sparse grids[J]. Number Algorithms, 1998, 18(3/4): 209–232.
DOI:10.1023/A:1019129717644
|
| [12] |
ZHANG L G, LU Z Z, CHENG L, et al.
Moment-independent regional sensitivity analysis of the complicated models with great efficiency[J]. International Journal for Numerical Methods in Engineering, 2015, 103: 996–1014.
DOI:10.1002/nme.v103.13
|
| [13] |
ZHAO Y G, ONO T.
Moment method for structural reliability[J]. Structural Safety, 2001, 23(1): 47–75.
DOI:10.1016/S0167-4730(00)00027-8
|
| [14] |
袁朝辉, 崔华阳, 侯晨光.
民用飞机电液舵机故障树分析[J]. 机床与液压, 2006(11): 221–223.
DOI:10.3969/j.issn.1001-3881.2006.11.075 YUAN Chaohui, CUI Huayang, HOU Chenguang. Fault tree analysis of civil aircraft electro-hydraulic actuator[J]. Machine Tool & Hydraulics, 2006(11): 221–223. DOI:10.3969/j.issn.1001-3881.2006.11.075 |
| [15] |
尹晓伟, 钱文学, 谢里阳.
系统可靠性的贝叶斯网络评估方法[J]. 航空学报, 2008, 29(6): 1482–1489.
DOI:10.3321/j.issn:1000-6893.2008.06.012 YIN Xiaowei, QIAN Wenxue, XIE Liyang. A method for system reliability assessment based on Bayesian networks[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1482–1489. DOI:10.3321/j.issn:1000-6893.2008.06.012 |
 2018, Vol. 50
2018, Vol. 50


