1996年,美国环球航空公司800号航班的一架B747客机在空中爆炸。1998年,瑞士航空公司的一架麦道11飞机失火后坠入大西洋。经调查,导线故障是这两起事故的最可能原因。由此,导线的安全性问题引起航空界的极大重视,并在运输类飞机适航标准中新增电气线路互联系统(Electrical wiring interconnection systems, EWIS)分部,要求在民机系统安全性评估中增加对导线失效的考虑。
机载导线横跨飞机各区域,受多个环境变量影响,不同环境区域下的导线其失效情况也不同,且没有足够的实际运营统计数据。因此,导线安全性基础数据是当前民机系统安全性评估的一个重点关注的问题。
由于此前普遍认为导线的失效率为零,国外也没有足够重视导线失效数据的收集、统计和研究工作。因此,为解决导线安全性基础数据问题,美国联邦航空局(Federal Aviation Administration, FAA)联合工业方针对导线安全性基础数据建立模型,提出了采用配对比较法将专家定性经验转化为定量信息,解决了多变量环境下的导线安全性基础数据问题[1-2]。但是,国内民机导线的设计、安装、维护和运营等情况与国外不同,国外专家依据本国情况得出的定性经验及数据并不适用于国内航空工业实际水平,并且所采用的配对比较模型是传统的Bradley-Terry模型[3-4]。该模型本身并不考虑定性信息对失效率估计的保守性影响,例如,对于专家打分数据出现两个环境比较无法得出优劣的情况,传统的Bradley-Terry模型并不能处理此类定性信息。
本文在FAA方法基础之上,选择适用于国内民机导线失效的典型环境,并且新增对环境变量之间相关性的考虑,建立导线安全性基础数据改进模型。同时,对多个配对比较模型进行分析,优选失效率估计保守性较高的配对比较模型,从而建立适用于国内运输类飞机导线安全性基础数据的通用模型。
1 导线安全性基础数据模型导线的主要功能是传递能量(信号或电能),因此,考虑两种常见的失效模式:短路和断路。本文仅涉及金属线本身的初始失效,不考虑其进一步发展成电弧放电和着火失效。根据短路和断路两种失效模式分别建立失效率模型。假设飞机导线的寿命服从指数分布,并且两种失效模式相互独立。则导线的失效率为短路和断路两种失效模式的失效率之和。导线寿命分布的概率密度函数为
| $ f\left( {{t_i}\left| {{\lambda _i}} \right.} \right) = {\lambda _i}{{\rm{e}}^{ - {\lambda _i}{t_i}}} $ | (1) |
式中:i是指导线不同的失效模式;λi是指定失效模式所对应的失效率。
导线失效率与多个环境变量有关,是各种环境变量的函数,采用X表示环境变量。根据比例风险模型[5],则失效率λ为这些环境变量的组合函数,表示如下
| $ \begin{array}{*{20}{c}} {\lambda = \exp \left( {{\beta _0} + \sum\limits_{i = 1}^n {{\beta _i}{X_i}} } \right) = }\\ {\exp \left( {{\beta _0} + {\beta _1}{X_1} + {\beta _2}{X_2} + {\beta _3}{X_3} + \cdots + {\beta _n}{X_n}} \right)} \end{array} $ | (2) |
式中n取1至m(典型失效环境数量)之间的任何数。
比例风险模型是生存分析中一种重要的回归模型,是用于研究多因素对生存时间影响的半参数模型。它不要求样本的生存时间服从特定的分布,也可以分析删失数据,这样大大降低了运用的烦琐性。
对于导线失效,各环境影响因素之间可能存在相关性。因此,将导线失效模型进一步精确为
| $ \lambda = \exp \left( {{\beta _0} + \sum\limits_{i = 1}^n {{\beta _i}{X_i}} + \frac{1}{2}\sum\limits_{i,j = 1,i \ne j}^n {{\theta _{ij}}{X_i}{X_j}} } \right) $ | (3) |
式中θij=θji是Xi与Xj间的相关系数,θ={θij}i,j=1~ni≠j,当Xi与Xj相互独立时,θij=0。对式(3)取对数, 得
| $ \ln \lambda = {\beta _0} + \sum\limits_{i = 1}^n {{\beta _i}{X_i}} + \frac{1}{2}\sum\limits_{i,j = 1,i \ne j}^n {{\theta _{ij}}{X_i}{X_j}} $ | (4) |
此时,只要确定式(4)的所有系数β,θ,则可计算出不同环境下给定失效模式的导线相对失效率。
2 导线典型失效环境导线跨越飞机多个环境区域,其失效受多个因素影响,环境区域的情况不同,导线失效率也不同。因此,首先要对影响导线失效的环境因素和典型失效环境进行研究。
2.1 影响导线失效的环境因素导线失效的影响因素主要考虑导线特性、线束特性和区域特性3个方面。导线特性用来描述单根导线本身的属性;线束特性用来描述线束的属性;区域特性用来描述线束所处工作环境的属性。经研究确定,对导线失效具有较大影响的环境变量包括导线线规、导体材料、绝缘类型、死接头、线束方向、线束规格、线束保护、线束弯曲半径、运营/维护频率、温度/气压、振动、是否与腐蚀液体接触以及是否与导电液体接触共13个。各个环境变量的分类根据飞机具体情况确定,如表 1所示。
| 表 1 影响导线失效的环境因素及其分类 Table 1 Environmental factors and their classifications contributing to wire failure |
2.2 导线典型失效环境
若按照环境变量进行组合,会有非常多的环境,而有些环境在现实飞机中并不存在。此外,即使在实际存在的环境中,仍有许多环境没有相应的实际使用数据。因此,本文选择有限数量的环境进行研究。根据确定的环境变量及其分类,经与导线相关专家讨论,确定了18个具有代表性的典型失效环境,如表 2所示。
| 表 2 民机导线典型失效环境 Table 2 Typical wiring failure environments of civil aircraft |
3 专家对比评判
在有大量现场使用数据或试验数据的条件下,根据导线失效模型,假设所有环境变量均两两相关,需建立(n2+n+2)/2个独立的方程,则可联立计算出相应的系数β和θ值。但由于这些数据很难获得,难以建立方程组来求解模型系数。为此,本文根据基于配对比较的专家评判和数理统计方法来建立导线失效模型。
导线相对失效率的计算取决于专家对各环境失效情况的定性评判结果。而所得的相对失效率直接影响模型系数的取值。因此,专家的选取及其打分结果的有效性至关重要。为使定性、定量转换结果更加精确,本文邀请来自国内局方、主机厂、航空公司等从事民机导线设计、维修、制造和试验等各个方面、具有丰富经验(部分专家具有40年左右的相关经验)的17位导线专家对导线典型失效环境进行对比评判。
3.1 典型失效环境对比评判导线专家分别针对短路和断路两种失效模式,对典型失效环境进行两两对比评判,即每次针对给定的两种典型失效环境判断哪个环境更加容易导致导线失效。为此,将典型环境对比评判表的格式设计成如表 3所示的样式。
| 表 3 典型失效环境对比评判表 Table 3 Comparison judgment with typical failure environments |
3.2 环境变量严重程度评判
在进行导线失效模型系数计算之前,需要求解出所有相对失效率λ和相关变量X。这里,将X看作每个环境变量对导线失效影响严重程度的几何平均值。可由专家打分得出每个X,评判表可设计如表 4形式。
| 表 4 环境变量严重程度评判表 Table 4 Judgment of the severity of environmental variables |
以导线线规为例,如表 5所示,设18~22为基准值1。若认为0~8比18~22相对不容易发生短路(断路)失效,并且这个相对程度非常大,可以认为取值为⑧,则在0~8线规左侧标记为⑧;若认为10~16线规比18~22相对更容易发生短路(断路)失效,并且这个相对程度很小,可以认为取值为②。
| 表 5 导线线规严重程度评判例表 Table 5 Judgment example of the severity of wire gauge |
3.3 环境变量相关性评判
根据已确定的所有环境变量,利用专家经验判断两两环境变量之间的相关性,即初步确定导线失效模型中的系数θ。设环境变量xi和xj,若xi与xj具有相关性,则θij=θji≠0(为方便起见,将θij设为1);若xi与xj无关,则θij=θji=0。环境变量两两相关性评判表可设计如表 6所示。在进行导线失效模型系数估计时,可先将模型中θij为0的项去掉,再利用计算得到的相对失效率λ和相关变量X通过回归方法求解模型系数β和非零θ值。
| 表 6 环境变量相关性评判表 Table 6 Judgment of the correlation of environmental variables |
3.4 专家评判结果有效性与一致性检验
专家评判结果是导线失效模型的输入,直接影响模型系数计算的精确程度。为避免所选专家的评判过程随意性强或专家状态不佳等情况,使用David[6]和Kendall等[7]方法对专家评判结果进行检验,分别判断各专家数据的有效性和所有专家数据的一致性,剔除结果不合理的专家。模型系数的求解仅使用通过有效性检验的专家数据。
(1) 专家数据有效性检验
专家数据有效性检验的目的是分析每个专家的评判是通过正确推理还是随机给出。这通过各专家评判结果中出现判断循环的次数得出。判断循环指的是如果专家判断失效环境E1要严重于失效环境E2、E2严重于E3、而E3严重于E1时,这就形成一个判断循环,该循环违反了传递原则。专家在进行大量评判工作时可能出现一些判断循环,可通过以下公式计算循环个数
| $ c\left( r \right) = \frac{{n\left( {{n^2} - 1} \right)}}{{24}} - \frac{1}{2}\sum\limits_{i = 1}^n {{{\left( {{N_r}\left( i \right) - \frac{1}{2}\left( {n - 1} \right)} \right)}^2}} $ | (5) |
当原假设为专家以随机方式进行评判时,Kendall针对n=2, …, 10的情况,提出了c(r)值超出一定限度的概率表。而对于任意n值, Kendall提出以下统计量
| $ \begin{array}{*{20}{c}} {c'\left( r \right) = \frac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{{{{\left( {n - 4} \right)}^2}}} + \left( {\frac{8}{{n - 4}}} \right) \times }\\ {\left[ {\left( {\frac{1}{4}{\rm{C}}_3^n - c\left( r \right) + \frac{1}{2}} \right)} \right]} \end{array} $ | (6) |
当n>7时,该统计量服从自由度为(n(n-1)(n-2))/(n-4)2的卡方分布。统计量可用于检验原假设(专家评判是随意的)和备选假设(专家评判是经过合理推理的)。可以使用此统计量对标准单边假设进行检验。如果原假设在5%的显著性水平下不被拒绝,则该专家评判结果应被剔除。
(2) 专家数据一致性检验
专家数据一致性是指众多专家对同一问题判断结果的趋同性。对一致性的检验也可以通过统计来检验。N(i, j)表示认为Ei严重于Ej的专家个数。假设所有专家的一致结果都是偶然的,为了对该假设进行检验,Kendall定义一致性系数u为
| $ u = \frac{{2\sum\limits_{i = 1}^n {\sum\limits_{j = 1,j \ne i}^n {{\rm{C}}_{N\left( {i,j} \right)}^2} } }}{{{\rm{C}}_e^2{\rm{C}}_n^2}} - 1 $ | (7) |
在该假设下,对于较小的n和e值,提出
| $ u' = \frac{{4\left[ {\sum\limits_{i = 1}^n {\sum\limits_{j = 1,j \ne i}^n {{\rm{C}}_{N\left( {i,j} \right)}^2} } - \frac{1}{2}{\rm{C}}_e^2{\rm{C}}_n^2\left( {\frac{{e - 3}}{{e - 2}}} \right)} \right]}}{{e - 2}} $ | (8) |
当原假设为所有专家一致性结果都是出自偶然时,u′近似服从自由度为C2ne(e-1)/(e-2)2的卡方分布。
4 导线安全性基础数据模型估计为保证安全性,需要选择趋向保守的失效率。本文对Davidson[8],Rao-Kupper[9]和weighted Bradley-Terry(WBT)等[10]配对比较模型进行对比分析,研究其置信区间的差异,确定模型对失效率估计的保守性。由于WBT与前两种模型都能处理专家打分数据出现两个环境比较无法得出优劣的定性信息,但其计算效率高,最终采用该模型作为估计导线相对失效率的优选模型。
4.1 专家数据检验本文邀请了17位导线领域专家对选取的18个环境进行了两两对比评判(每个失效模式包含153个对比表格),并统计评判结果。根据式(5—8),专家数据的有效性和一致性检验结果如表 7所示。
| 表 7 专家数据有效性和一致性检验结果 Table 7 Test results of the effectiveness and consistency of expert judgment |
计算表明,所有专家结果均有效且一致性检查合格。这意味着所有专家的判断信息均可使用。
4.2 导线相对失效率估计将专家评判数据作为导线相对失效率计算模型的输入,利用优选模型——WBT模型对导线失效率进行估计,实现数据的定性、定量转换。估计结果如表 8所示。
| 表 8 典型失效环境相对失效率 Table 8 Relative failure rates of typical failure environments |
4.3 导线相关变量求解
将17位专家对表 4中的判断结果进行汇总,并求出各个环境变量严重程度的几何平均值Xi。以断路时导线线规为例,统计结果如图 1所示。

|
图 1 专家对断路时导线线规严重程度判断结果 Figure 1 Expert judgment result of the severity of wire gauge under open failure mode |
部分导线相关变量X的取值如表 9所示。
| 表 9 导线相关变量取值 Table 9 Coded values for wire correlation variables |
4.4 导线失效模型系数求解
根据专家对环境变量相关性的评判结果,初始模型系数θ12=θ21=1,θ68=θ86=1和θ10, 11=θ11, 10=1,其他θ初始值均为0,则令X1X2为X14,X6X8为X15,X10X11为X16。结合利用WBT模型计算得到的各典型失效环境相对失效率和各环境变量对应的相关变量X离散值,对导线失效模型进行回归分析。
针对短路失效模式,利用逐步回归方法[11]筛选对模型回归贡献较大的环境变量,即剔除某些环境变量后回归估计结果均能通过显著性检验,这里将X5, X6, X7, X8, X13, X14,X15剔除。同时,根据Cook’s[12]距离分析,剔除对回归结果影响较大的第15个环境数据,如图 2所示(Obs.number表示环境)。此外,利用Shapiro-Wilk[13]检验方法来检验误差的正态性。

|
图 2 短路失效模式下的Cook’s距离图 Figure 2 Cook's distance under shorting failure mode |
由表 10可知,环境变量和回归关系基本通过显著性检验(Pr < 0.05,Sig. F < 0.05),回归模型拟合优度较好(R方和调整R方接近于1),误差通过正态性检验(p-value>0.05)。
| 表 10 短路失效模式下模型系数估计及检验结果 Table 10 Model coefficient estimation and test results under shorting failure mode |
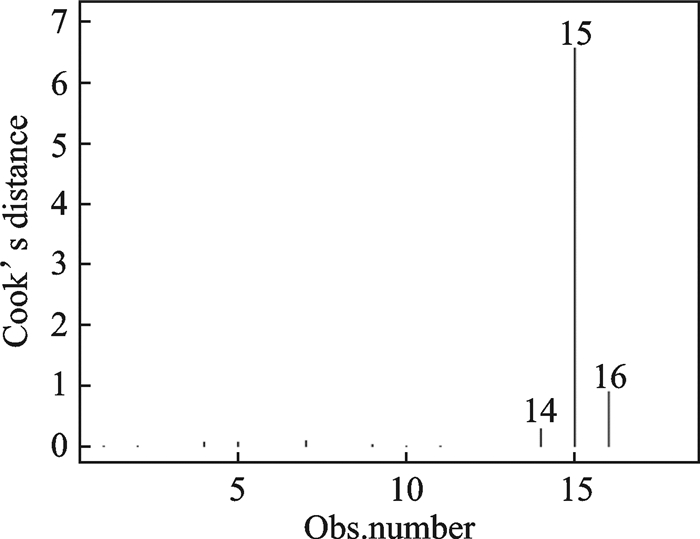
同理,针对断路失效模式,利用逐步回归方法剔除环境变量X2, X3, X7, X8, X13, X14, X15。根据Cook’s距离分析,剔除对回归结果影响较大的第15个环境数据,如图 3所示。利用Shapiro-Wilk检验方法来检验误差的正态性。
|
图 3 断路失效模式下的Cook’s距离图 Figure 3 Cook's distance under open failure mode |
由表 11可知,环境变量和回归关系均通过显著性检验(Pr < 0.05,Sig. F < 0.05),回归模型拟合优度较好(R方和调整R方接近于1),但没能通过误差正态性检验(p-value < 0.05)。
| 表 11 断路失效模式下模型系数估计及检验结果 Table 11 Model coefficient estimation and test results under open failure mode |
为通过误差正态性检验,可进一步优化式(4)所示的导线失效模型,即将Y=f(X, β, θ)改进为Y2=f(X, β, θ)。由于lnλ均为负值,则
| 表 12 模型系数估计结果 Table 12 Model coefficient estimation results |
4.5 模型修正
根据专家评判数据,由优选配对比较模型计算得到的失效率是相对失效率,需要利用实际失效数据信息对相对失效率进行修正,从而得到真实的失效率。模型修正系数的获取方法如下
| $ 模型修正系数\;\alpha = \frac{{某一环境下的实际失效率}}{{某一环境下的相对失效率}} $ |
本文利用飞机导线总失效率和相对失效率的中位值来计算修正系数。本文对2010—2014年FAA的实际统计数据——使用困难报告(Service difficulty reports,SDR)进行分析,统计FAA这5年中所有机型导线发生短路和断路失效的总失效率,计算结果如表 13所示。
| 表 13 实际失效率计算结果 Table 13 Calculation results of actual failure rate |
选取表 8中短路和断路相对失效率的中位值0.033 2和0.042 6作为实际失效率所对应的相对失效率。则短路修正系数αs和断路修正系数αo为别为
| $ {\alpha _{\rm{s}}} = \frac{{3.330\;9 \times {{10}^{ - 11}}}}{{0.033\;2}} \approx 1.003\;3 \times {10^{ - 9}}/\left( {{\rm{hr}} \cdot {\rm{ft}}} \right) $ |
| $ {\alpha _{\rm{o}}} = \frac{{2.192\;1 \times {{10}^{ - 11}}}}{{0.042\;6}} \approx 5.145\;8 \times {10^{ - 9}}/\left( {{\rm{hr}} \cdot {\rm{ft}}} \right) $ |
根据式(3)可知,任一环境下的实际失效率为
| $ \begin{array}{l} {\lambda _{\rm{s}}} = \exp \left\{ {24.540\;6 + 2.091\;0{X_1} - 34.449\;5{X_2} - } \right.\\ \;\;\;\;\;\;0.538\;4{X_3} + 0.704\;2{X_4} + 0.458\;3{X_9} + \\ \;\;\;\;\;\;1.335\;6{X_{10}} + 0.776\;0{X_{11}} + 0.544\;6{X_{12}} - \\ \;\;\;\;\;\;\left. {0.294\;7{X_{16}}} \right\} \times 1.003\;3 \times {10^{ - 9}} \end{array} $ |
| $ \begin{array}{l} {\lambda _{\rm{o}}} = \exp - \left\{ {61.695\;0 - 1.770\;6{X_1} - 6.367\;3{X_4} - } \right.\\ \;\;\;\;\;\;\;3.372\;1{X_5} - 1.610\;0{X_6} - 3.499\;2{X_9} - \\ \;\;\;\;\;\;\;11.240\;2{X_{10}} - 5.941\;0{X_{11}} - 4.392\;2{X_{12}} + \\ \;\;\;\;\;\;\;{\left. {2.385\;7{X_{16}}} \right\}^{1/2}} \times 5.145\;8 \times {10^{ - 9}} \end{array} $ |
在借鉴FAA民机导线建模方法的基础上,本文提出了一种构建导线安全性基础数据改进模型的方法。该模型与FAA的不同之处在于,其考虑了各环境影响因素之间的相关性。在确定典型失效环境后,通过专家对比评判获得导线失效的定性数据,该数据通过了有效性和一致性检验。为将定性数据转换为适用于模型建立的定量数据,本文优选了配对比较模型,并利用逐步回归法求解模型系数。计算结果表明模型通过了显著性检验和误差正态性检验,且拟合度较好。最后,利用由实际统计数据计算得到的实际失效率对模型进行了修正。
| [1] |
U.S.Department of Transportation Federal Aviation Administration. Development of the electrical wiring interconnection system risk assessment tool: DOT/FAA/AR-09/47[R].Springfield: U.S. Department of National Technical Information Services (NTIS), 2010. |
| [2] |
MAZZUCHI T A, LINZEY W G, BRUNING A.
A paired comparison experiment for gathering expert judgment for an aircraft wiring risk assessment[J]. Reliability Engineering & System Safety, 2008, 93(5): 722–731.
|
| [3] |
BRADLEY R A, TERRY M E.
Rank analysis of incomplete block designs[J]. Biometrika, 1952, 39(3/4): 324–345.
DOI:10.2307/2334029
|
| [4] |
FORD L R.
Solution of a ranking problem from binary comparisons[J]. American Mathematical Monthly, 1957, 64(8): 28–33.
DOI:10.2307/2308513
|
| [5] |
LAWLESS J F.
Statistical models and methods for lifetime data[J]. Biometrics, 1982, 99(465): 298–299.
|
| [6] |
DAVID H A.
The method of paired comparisons[M]. New York: Oxford University Press, 1988.
|
| [7] |
KENDALL M, GIBBONS J.
Rank correlation methods[M]. New York: Oxford University Press, 1990.
|
| [8] |
DAVIDSON R R.
On extending the Bradley-Terry model to accommodate ties in paired comparison experiments[J]. Journal of the American Statistical Association, 1970, 65(329): 317–328.
DOI:10.1080/01621459.1970.10481082
|
| [9] |
ALTAF S. Statistical analysis of the paired models through bayesian approach[D]. Islamabad: Quaid-i-Azam University, 2009. |
| [10] |
ABBAS N, ASLAM M.
Extending the Bradley-Terry model for paired comparisons to accommodate weights[J]. Journal of Applied Statistics, 2011, 38(3): 571–580.
DOI:10.1080/02664760903521450
|
| [11] |
HU T H.
A stepwise regression algorithm for high-dimensional variable selection[J]. Journal of Statistical Computation & Simulation, 2015, 85(9): 1793–1806.
|
| [12] |
JAYAKUMAR G S D S, SULTHAN A.
Exact distribution of Cook's distance and identification of influential observations[J]. Hacettepe University Bulletin of Natural Sciences & Engineering, 2015, 44: 165–178.
|
| [13] |
HANUSZ Z, TARASINSKA J.
Simulation study on improved Shapiro-Wilk tests for normality[J]. Communications in Statistics Simulation & Computation, 2014, 43(9): 2093–2105.
|
 2018, Vol. 50
2018, Vol. 50


