航空发动机由于特定的工作原理，其高压涡轮等核心机长期在高压高温等恶劣工况中运转，叶片承受各种机械应力和热应力；且由于为提高叶片的散热效果，涡轮叶片被制成表面有通风孔的空心状薄壁件，很容易发生疲劳裂纹。疲劳裂纹可以通过荧光检查、磁粉检查、超声波检查以及X射线检查等检查措施来发现。对于航线检查、定检等非大修损伤检测，机务维修部门一般用孔探技术检测叶片裂纹。裂纹尺寸在设计的损伤容限内可以继续使用，超过一定尺寸的裂纹就意味着叶片失效。根据发动机的有关使用维修资料统计，燃气涡轮发动机叶片断裂是发动机发生故障并可能导致航空事故的重要因素之一^[1]。故涡轮叶片检查、监测和维修是发动机结构部件检修的重要工作之一。这些检查工作分布在发动机寿命周期内的不同阶段(如航前航后检查、定检、大修以及事后维修等)，大量的检测及维修记录零散分布于工程维修单中，并没有被充分反馈到发动机的寿命预测和维修决策之中。工程师们将这些离散的、小样本且受到很多外界不可控因素的影响(人为因素、自然条件和设备精度等)的检测信息作为一种工程经验用做判断依据显然是不科学的，有时甚至是错误的。因此，检修数据在发动机的健康管理中一直受到忽视。本文拟从工程实际检修数据的统计分析及发动机结构部件的物理失效规律方面探讨和研究如何利用这些检修数据对发动机进行维修决策的方法论，为工程师对发动机结构部件的维修决策提供科学依据。

由于航空发动机对结构完整性和功能可靠性要求的特殊性，其维修策略一般都采用视情维修。因此，从运行维护和检修决策的角度，国内外很多学者都基于部件/系统的状态监控信息对发动机进行视情维修决策研究，涉及到的主要理论有概率论、数理统计、更新过程、再生过程、马尔可夫链、Gamma过程、Poisson过程和鞅等基础理论；相关模型包括状态空间模型^[2]、延迟时间模型^[3]、计数过程模型^[4]以及比例危险模型^[5]等；并结合相关约束条件(例如，轮盘、叶片等关键旋转部件的时寿限制、局方发布的适航指令AD或者设备供应商发布的服务公告SB等软时限要求)，应用各种智能优化算法(如遗传算法^[6]、模拟退火算法^[7]、启发式算法^[8]、线性^[9]或非线性规划^[10]、多目标决策方法^[8]以及马尔可夫决策的迭代寻优算法^[11]等)，优化有关决策变量(包括维修间隔^[12]、维修等级^[13]、维修工作范围^[14]以及维修状态阈值^[15]等)，得到最优或局部最优目标值。文献[16]根据航线检修数据应用时间延迟模型对发动机某子系统在多目标约束条件下的检修决策进行了优化研究。上述研究方法主要都是基于数据驱动的方法，且很多都是基于大量连续监测数据进行发动机的检修决策研究。国内外也有一些学者从发动机设计角度出发，通过物理/性能模型或损伤容限准则来推演其性能衰退趋势和结构损伤扩展规律，从而达到检修预测的目的^[17-21]。融合航线检查数据和物理失效规律对发动机结构部件进行检修决策的研究还比较鲜见。因此，本文将根据航线检查数据及其特点拟提出一种新的结构件损伤检修决策方法。

结构部件检查不同于系统和结构监测。结构检查是定时(计划性)或不定时(非计划性)的、离散的检测，检测目的是发现结构部件是否损伤或失效。其检测结果一般有两种情况：(1)对于可达性较差的原位测量部件，或是成败型部件，检查是否损伤(或失效)，记录损伤(或失效)的部件数，例如涡轮叶片、直接可替换单元(LRU)；(2)对于通过检测部件的特征参数来判别是否损伤(或失效)，测量部件损伤(或失效)的尺寸，并记录损伤(或失效)的部件数，例如：涡轮叶片、叶盘等。本文调研收集到的发动机涡轮叶片损伤检测数据主要包括在不同的检查时刻T，通过孔探等检查手段发现一组叶片n中有k个叶片损伤失效，利用叶片损伤检测数据并应用物理退化模型对涡轮叶片进行仿真分析和检修策略优化。

1 基于检查数据的失效概率分布 1.1 基于二项分布的似然函数建模

根据发动机涡轮叶片的实际损伤检查数据形式(t，n，k)，在检查时刻t，n个涡轮叶片中有k个叶片发生失效时的概率质量函数为

$ \begin{gathered} P(k\;{\text{failures in}}\;n\;{\text{components}} \hfill \\ |F\left( t \right)) = \hfill \\ \left( \begin{gathered} n \hfill \\ k \hfill \\ \end{gathered} \right){\left( {F\left( t \right)} \right)^k}{\left( {1 - F\left( t \right)} \right)^{\left( {n - k} \right)}} = \hfill \\ \frac{{n!}}{{k!\left( {n - k} \right)!}}{\left( {F\left( t \right)} \right)^k}{\left( {1 - F\left( t \right)} \right)^{\left( {n - k} \right)}} \hfill \\ \end{gathered} $

(1)

式中:F(t)为涡轮叶片的累积失效概率函数，且假设$F\left( t \right) = 1 - {{\text{e}}^{ - {{\left( {\frac{t}{\beta }} \right)}^\alpha }}}$，其概率密度函数为$f\left( t \right) = \frac{\alpha }{\beta }{\left( {\frac{t}{\beta }} \right)^{\alpha - 1}}{{\text{e}}^{ - {{\left( {\frac{t}{\beta }} \right)}^\alpha }}}, \alpha, \beta $分别为F(t)的形状参数和尺寸参数。随着检查数据的增多，当检查数据以系列s=(s₁, s₂, …, s_i, …, s_N)递增时，根据式(1)，得到整个检查过程的似然函数为

$ \begin{gathered} L = \prod\limits_{i = 1}^N {{L_i}\left( {{s_i}|\alpha , \beta } \right) = \prod\limits_{i = 1}^N {\frac{{{n_i}!}}{{{k_i}!\left( {{n_i} - {k_i}} \right)!}} \cdot } } \hfill \\ {\left( {{F_\iota }\left( {{t_i}} \right)} \right)^{{k_i}}}{\left( {1 - {F_\iota }\left( {{t_i}} \right)} \right)^{\left( {{n_i} - {k_i}} \right)}} \hfill \\ \end{gathered} $

(2)

式中: s_i =(t_i, n_i, k_i)，i为顺序检查序数；t_i, n_i, k_i分别表示第i次检查时间、第i次检查时的涡轮叶片总数和第i次检查时的失效叶片数；$ F\left( {{t_i}|\alpha ,\beta } \right) = \int_{{{_{{t_i}}}_0}} {f\left( {\tau {\text{|}}\alpha ,\beta {\text{ }}} \right){\text{d}}\tau } $表示在t_i时刻涡轮叶片的累积失效概率, f(t)为概率密度函数。

1.2 基于贝叶斯更新方法的参数估计

根据1.1节中所述，假设涡轮叶片部件的寿命服从威布尔分布，由于人们对叶片失效分布函数中的参数分布知之甚少，一般假设待估计参数的先验分布为均匀分布，形状参数α先验分布的范围根据威布尔分布的一般形状参数范围确定^[22]，尺寸参数β先验分布的范围根据检查数据、设计寿命以及工程师的经验确定。由贝叶斯参数更新原理^[23]，应用Metropolis-Hastings抽样法(M-H法)^[24]，得到发动机涡轮叶片失效分布函数的参数估计值($\hat \alpha ,\hat \beta $)，由此确定的涡轮叶片寿命t分布函数如图 1所示。当初始检查数据较少时，失效分布函数的不确定性较大，随着检查数据的增加和分布函数参数的更新，失效分布函数更趋于符合实际。需要指出的是，失效分布函数本质上包含了叶片的材料属性、服役承载情况以及环境变化等各种因素的影响。因此，通过收集更多的检查数据和参数递推更新，失效分布函数的分散程度趋于变小，亦即失效分布能更加确切地间接反映叶片的物理属性和服役环境等因素对疲劳寿命的影响。

2 基于物理失效模型的检修策略原理 2.1 裂纹增长反演分析

对于涡轮叶片在初始可检裂纹至临界失效裂纹的稳定扩展区，利用Paris公式^[25]有

$ {\text{d}}a/{\text{d}}t = C{(\Delta K)^m} = C{(r\Delta \sigma \sqrt {{\text{π }}a} )^m} $

(3)

式中:C, m是叶片的材料基本参数，一般由实验确定。r是叶片的修正系数，一般与叶片裂纹的尺寸有关，可由应力强度因子手册查得，对于单边裂纹无线大板，r取值为1.12。Δ σ是叶片承受的应力载荷幅值，a为叶片裂纹长度，t为发动机的循环次数(或寿命)，ΔK是应力强度因子幅值，π为常数。式(3)通过积分并整理后，得到

$ \begin{gathered} {t_{\text{d}}} = {t_{\text{c}}} - \frac{1}{{C{{\left( {r\Delta \sigma \sqrt {\text{π }} } \right)}^m}\left( {0.5m - 1} \right)}}{\text{ }} \hfill \\ \left( {\frac{1}{{a_{\text{d}}^{0.5m - 1}}} - \frac{1}{{a_{\text{c}}^{0.5m - 1}}}} \right){\text{ }} \hfill \\ \end{gathered} $

(4)

式中: a_c, a_d分别为临界裂纹失效长度和初始可检裂纹长度，t_c, t_d分别为a_c, a_d对应的发动机循环次数(或寿命)。

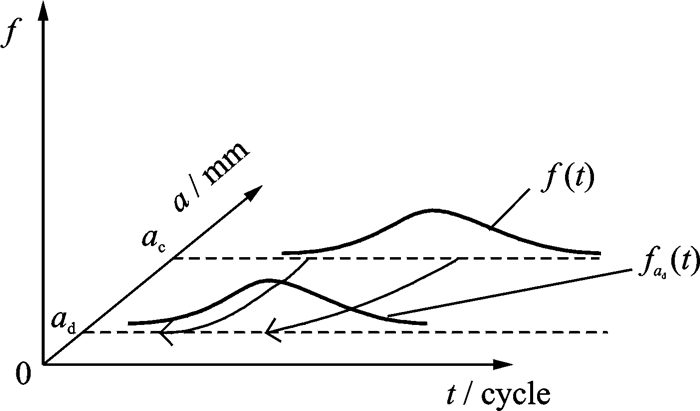
由第1节中所得的叶片在临界失效裂纹长度a_c时的失效分布函数，抽样得到模拟的叶片寿命。根据式(4)和初始可检裂纹长度a_d以及叶片的材料属性、载荷谱等参数，由裂纹逆增长过程得到叶片在初始可检裂纹长度处的寿命及其统计分布，其示意图如图 2所示。

需要指出的是，初始可检裂纹长度a_d是一随机变量，它与检测方法、手段和条件等因素以及检测概率有关；同时，裂纹增长反演过程中需保持裂纹失效分布函数的不变性，这样才能保证材料属性、受载情况以及环境等影响因素不会使失效分布函数发生变化。这种不变性原则本文未能在理论上给予证明，但下文中有专门的说明。

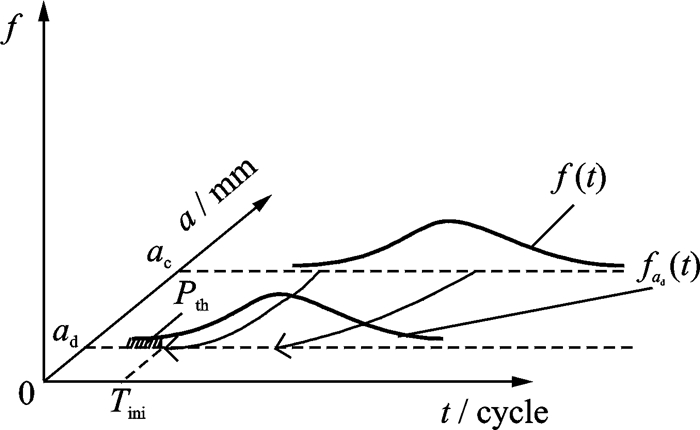
2.2 初检时刻确定

航空维修手册中关键重要部件的初检时间一般都根据有限的实验结果和统计推断，在保证一定失效概率的条件下确定某一固定的检查间隔。但对于航空公司来说，发动机的运行环境不同，其初检时机也不尽相同，因此需要根据发动机涡轮叶片的运行损伤检查数据确定更符合实际运行环境的检修时间。假设由式(4)反演仿真得到的初始可检裂纹长度a_d所对应的寿命t服从参数为(α′, β′)的威布尔分布，其概率密度函数为f_ad(t)，通过数据拟合，得到参数(α′, β′)的估计值($\hat \alpha ',\hat \beta '$)。根据涡轮叶片的完整性概率要求，设定某一累计分布阈值P_th(一般设定P_th=0.01或0.001，叶片完整性要求越高，P_th越小)，在概率密度曲线中P_th对应的时间即为初检时刻T_ini，示意图如图 3所示。即

$ \int_0^{{T_{{\text{ini}}}}} {f_{a_{\text{d}}}\left( t \right){\text{d}}t} = {P_{{\text{th}}}} $

(5)

在f_ad(t)服从参数为($\hat \alpha ', \hat \beta '$)的威布尔分布的条件下，式(5)转化为

$ 1 - \exp\left[ { - {{\left( {\frac{{{T_{{\text{ini}}}}}}{{\hat \alpha '}}} \right)}^{\hat \beta '}}} \right] = {P_{{\text{th}}}} $

(6)

根据式(6)即可计算得到初检时刻T_ini。当然，用这种方法确定的初检时刻实际上也是比较保守的，这个初检时刻包含了裂纹的起始过程和早期裂纹扩展过程，而裂纹的起始过程和早期裂纹扩展过程建模目前还比较困难，目前没有比较统一的模型可以描述此过程。此方法确定的T_ini的物理意义在于：在初检时刻T_ini之前，通过一定的检测方法和手段都基本上不太可能检测到该裂纹；在T_ini之后，通过某些检测方法和手段有一定的概率可以检测到该裂纹，裂纹扩展可以视为稳定扩展阶段，即可用Paris, Forman等模型描述。在没有完全理解裂纹在起始阶段产生和在早期扩展阶段微小裂纹扩展机理的情况下，这种人为假设和推理符合工程实际。

由式(6)求得T_ini后，再根据式(4)可以得到在T_ini处的裂纹长度a的仿真模拟值，即

$ \begin{gathered} a = \{ a_{\text{c}}^{1 - 0.5m} - ({T_{\text{c}}} - {T_{{\text{ini}}}})[C(r\cdot \hfill \\ \;\;\;\;\;\;\;\;\;\;\Delta \sigma \sqrt {\text{π }} {)^m}\left( {1 - 0.5m} \right)]{\} ^{\frac{1}{{1 - 0.5m}}}} \hfill \\ \end{gathered} $

(7)

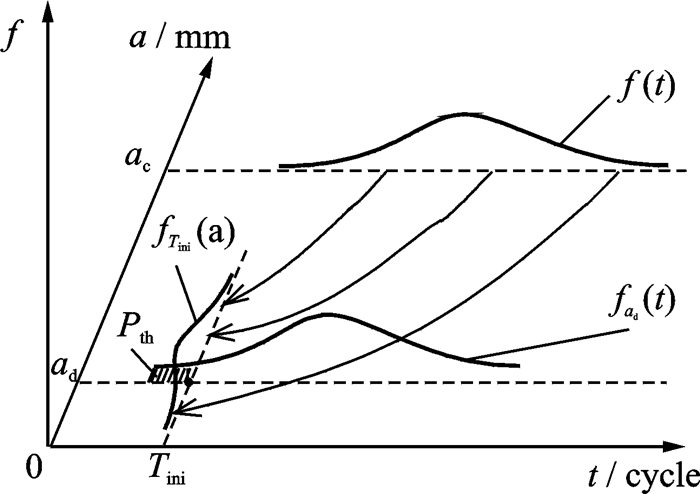
式中，T_c是根据f(t)的累积分布函数抽样得到的模拟失效时间，并通过数据拟合得到其概率密度函数f_Tini(a)，其示意图如图 4所示。

2.3 裂纹增长仿真分析

对由式(7)中计算得到的裂纹长度模拟值拟合而成的f_Tini(a)进行随机抽样，得到在T_ini时刻的各初始裂纹长度a，根据式(3)，${\text{d}}a = C{\left( {r\Delta \sigma \cdot \sqrt {\text{π }} a} \right)^m}{\text{d}}t$，经过一个循环步长增量dt后，得到当前循环数下t = t+ dt的裂纹长度a = a + da。在经过一个或多个重复检查间隔ΔT后，叶片可能已达到失效状态，也可能处于退化但还没有失效的状态。如果叶片在检查时处于失效状态，则叶片在计划寿命T_total内记为失效，如图 5中虚线箭头1所示退化路径(由此退化路径得到的寿命模拟值经拟合后其分布形状与f(t)基本吻合，即意味着从仿真角度验证了裂纹增长反演过程中裂纹失效分布函数的不变性)；如果叶片在检查时处于退化但还没有失效的状态，叶片裂纹不断扩展，直至叶片在计划寿命T_total时所处的检查状态，如图 5中虚线箭头2所示退化路径。

根据公式T_total－T_ini=nΔT(其中n为正整数，表示检查次数)，尝试不同的ΔT(对应叶片在寿命周期内不同的检查次数n值)和T_ini(不同的累计分布阈值P_th对应不同的初检时间T_ini)，通过仿真T_ini, n和ΔT三个参数的优化过程，得到叶片在计划寿命周期内不同的失效概率P_f，P_f的计算公式用如式(8)逼近

$ {P_f} \approx \frac{{{\text{number}}\;{\text{of}}\;a_{{T_{{\text{total}}}}}^{(i)}|a_{{T_{{\text{total}}}}}^{(i)} \geqslant {a_{\text{c}}}}}{M} $

(8)

式中:M为总仿真次数，a_Ttotal⁽ⁱ⁾表示第i次仿真裂纹扩展到T_total时的长度，i=1, 2, …, M。根据叶片在计划寿命周期内的可靠性要求，得到叶片的最佳重复检查间隔ΔT (即得到满足可靠性要求的初检时间和最少检查次数)。

值得注意的是，在某个检查时刻t，如果裂纹没有被发现，则根据式(3)裂纹不断增长，直至下一个检查时刻(t +ΔT)。若t < T_total且t+ΔT≥T_total时，则根据式(9)计算在[t, T_total]时间间隔内裂纹增长，即

$ \begin{align} & {{a}_{{{T}_{\text{total}}}}}=\{{{a}^{~}}_{t}^{1-0.5m}-({{T}_{\text{total}}}-t)[C(r\cdot \\ &\;\;\;\;\;\;\; \Delta \sigma ~\sqrt{\text{ }\!\!\pi\!\!\text{ }}~{{)}^{m}}\left( 0.5m-1 \right)]{{\}}^{~\frac{1}{1-0.5m}}} \\ \end{align} $

(9)

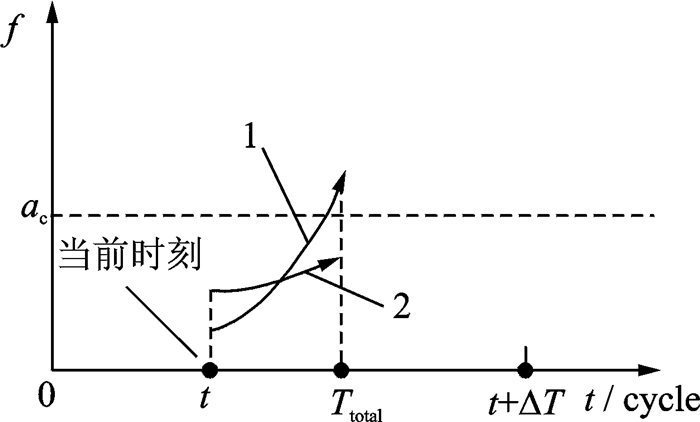
式中a_t表示在当前时刻t时的裂纹长度，其裂纹增长示意图如图 6所示，此时裂纹长度可能大于临界失效尺寸a_c(如图 6中扩展路径1所示)，也可能没有失效(如图 6中扩展路径2所示)。

根据以上分析步骤，建立计算流程图如图 7所示。

3 实例分析

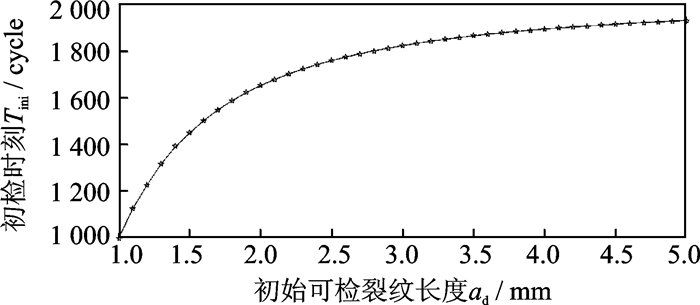
根据中国邮政航空公司CFM56-5B/P型航空发动机机队的现场检查数据，并根据发动机性能工程师的实践经验、对实际运行工况的描述和估计以及型号发动机叶片检查维修手册^[26]要求，且结合相关文献资料^[27]中对叶片材料参数的试验、检测和统计，在应用以上方法、流程过程中，相关参数取值如表 1所示(根据Paris方程裂纹增长过程及逐次检测时的裂纹长度，应用最小二乘法优化得到参数C和m的值，详见文献[27])。根据以上方法和相关参数设置，编制Matlab仿真程序，得到初始可检裂纹长度a_d和初检时间T_ini之间存在函数关系如图 8所示。从图 8中可以看出，初始可检裂纹长度包含了叶片裂纹检测孔探仪一般均能检测到的最小裂纹长度(1mm)到叶片失效的临界裂纹长度(5mm)区间，且随着初始可检裂纹长度的增加，初检时间变化趋于平缓。

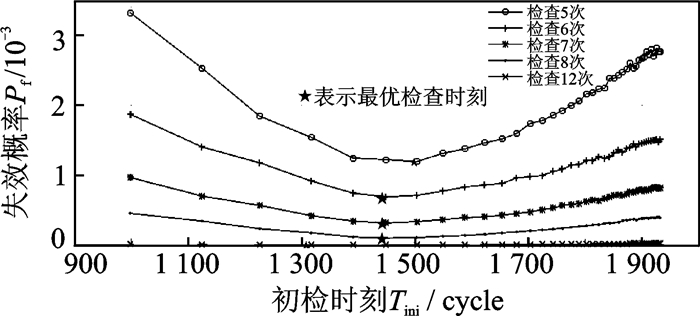
图 9是不同检查次数的初检时刻与失效概率之间的关系。从中可以看出，随着初检时间的推移，叶片的失效概率均有先降后增的趋势，因此初检时刻的选择可以使叶片的失效概率达到“拟最优”(所谓“拟最优”是指在当前考虑的各种模型因素和检查次数要求下，使叶片能达到的最小失效概率，如图 9中“ ★ ”所示)。这说明叶片在服役过程中首次检查不宜太早(如果首检时间太早，首检时扩展裂纹长度小，不易被检测到，后续的重复检查间隔长，也容易对裂纹叶片产生漏检)，首检亦不宜太迟(如果首检时间太迟，多数叶片的裂纹长度在首检时会接近甚至超过临界损伤值，尽管后续重复检查间隔缩短，但也会增加叶片在后续重复检查时的失效概率)，且随着叶片在寿命周期内检查次数的增多，“拟最优”失效概率也逐渐减小，对应的初检时刻非单调地趋于减小，这可能是因为初检时间对叶片失效概率的累计影响比重复检查间隔的变化对叶片失效概率的影响要大些。

允许失效概率[P_f]的选取一般要综合考虑失效引起的后果和防止失效采取相关安全措施的经济代价，邮政航空公司根据机队失效故障统计情况确定的可接受允许失效概率值可作为涡轮叶片的失效概率目标值，在满足仿真计算中“拟最优”失效概率值不大于允许的失效概率值[P_f]条件下，确定最少检查次数n_opt以及对应的首检时刻T_ini、初始可检裂纹长度a_d和重复检查间隔ΔT。在叶片失效概率分别不大于10^-3, 10^-4和10^-5的情况下，优化后的检测间隔见表 2。

4 结束语

叶片在服役过程中首次检查时间不宜太早，也不宜太迟，初检时间与重复检查间隔及其检查次数存在“拟最优”关系。由于发动机涡轮叶片损伤引起的事故易引发严重灾难，加强发动机叶片损伤检修频次的经济代价相对于由于发动机叶片损伤引起灾难性后果的代价程度还是较低的，因此建议将[10^-5]作为允许失效概率，在本文调研机队的计划运行周期内最少检查12次，且初检时间和重复检查间隔分别为1 371循环和307循环。由于发动机叶片结构的检查数据属于小样本问题，在分布函数中参数的收敛速度会比较缓慢，得到的叶片失效概率分布函数的分散性较大，且结构损伤模式多样化，本文所提方法在维修决策精度上可能比基于大量监测数据得到的维修决策要低。因此，本文作为一种探索性方法，需要在航线的日常检修中进行检验和验证。