2. 厦门大学航空航天学院, 厦门, 361005
2. School of Aerospace Engineering, Xiamen University, Xiamen, 361005, China
航空弹药的消耗预测、存储及运输问题是航空弹药供应保障的焦点和难点。随着科学技术的进步,战争模式的快速转换要求航空弹药的供给能动态完全满足航空部队的需要,而作为动态工作满足的基本条件就是对航空弹药消耗进行合理估计和预测。特别是航空弹药作为一种全程消耗的军需品,其供应保障的效率日益成为军方决策者关注的重点和焦点。航空弹药的消耗,特别是对未来一段时间的消耗估计是航空弹药供应链建立和运作的直接动力。了解航空弹药的消耗变化规律是研究其供应链运作方式、最优库存控制水平、弹药供应可靠性、弹药紧急补充方式的前提。对于航空弹药消耗的规律一般可以利用多年消耗的历史数据记录,进而通过数理统计的方法进行统计、分析、归纳,找到航空弹药消耗的一般规律。而训练消耗由于每个时期基本情况不同、政治背景不同以及武器装备和火力不同等原因导致其不能简单对航空弹药的训练消耗进行多元线性分析,而需要建立多因素影响的非线性模型。因此,采用科学的方法对航空弹药的消耗进行合理预测,对于切实提高航空弹药的供应保障效率具有积极的指导意义。
关于航空弹药的消耗预测问题,很多学者对其进行了深入研究。刘涛和彭世蕤[1]基于共轭梯度算法改进传统BP神经网络模型,进而对航空弹药消耗量进行预测,研究结果表明改进的BP神经网络模型能有效克服局部极值问题、快速提高网络收敛速度并且准确度高。陈利安等[2]利用多元线性回归预测、灰色预测和并联及串联灰色多元线性回归预测等多种模型来预测航空弹药平时消耗量,对比结果表明并联模型的预测具有非劣性,而串联模型能有效降低原始数据的随机性,提高模型预测精度。陶茜等[3]基于蚁群算法对目标进行聚类,并利用模糊综合评判法进行评判,进而确定攻击目标的航空弹药需求量,该方法为战时航空弹药的需求预测提供了理论依据。邱国斌[4]对战时航空弹药消耗特点进行统计分析,研究表明伽马分布对弹药消耗量的历史数据拟合效果较好。康宗宇等[5]提出一种基于贝叶斯方法的战时航空弹药预测模型,研究结果表明该模型能有效预测出未来阶段的战时航空弹药保障供应能力,且预测精度高。孙云聪和万华[6]选取反向传播(Back propagation,BP)网络模型和Elman网络模型对航空训练弹药需求量进行预测,研究结果表明Elman网络在收敛速度以及联想记忆方面都优于BP网络。周一鸣等[7]基于动态灰色模型对航空弹药的维修器材消耗量进行预测,研究表明动态灰色模型的运用能提高灰区间的白度且预测精度高于传统灰色模型。综上所述,针对航空弹药消耗预测问题,目前主要运用多元线性回归、神经网络以及灰色预测等传统模型。考虑到航空弹药消耗受到国际局势、国家战略发展需要往往呈现出非线性发展态势,同时神经网络主要是基于传统统计学知识解决样本无穷大问题,并且灰色模型对于非线性问题很难得到精确的预测结果,因此现有的预测模型具有一定的局限性,不能很好地解决航空弹药消耗预测问题。
支持向量机(Support vector machines,SVM)由于具有完备的理论基础以及较好的学习性能,并且能有效解决非线性等实际问题,近年来在字符识别[8]、气象预测[9]、太阳能耗[10]、股指期货[11]、知识转移[12]以及图像检索[13]等领域得到广泛运用。除了独立使用支持向量机来解决预测问题外,也有部分学者引入粗集理论(Rough sets,RS),将粗集与支持向量机融合来进行组合预测。粗集的优势在于对原始数据进行属性约简,通过消除冗余信息减少支持向量机学习与预测的负担,进而提高支持向量机预测的精度,获得更好的预测性能。在这方面,刘双印等[14]将粗集与支持向量机融合,提出了RS-SVM模型研究水质预测问题;汪莹和蒋高鹏[15]基于RS-SVM模型对煤矿安全风险问题进行了预测研究;孟宏鹏等[16]将粗集属性约简与支持向量机融合提高了变压器故障诊断准确率。
考虑到RS-SVM组合预测模型目前仅在水质检测、煤矿安全风险等少数领域有所运用,因此本文结合航空弹药训练消耗的特点,构建邻域粗糙集(Neighborhood rough sets,NRS)与支持向量机融合的NRS-SVM模型来对航空弹药训练消耗进行预测。NRS-SVM组合预测模型的优势在于通过邻域粗糙集属性约简技术提高支持向量机的预测性能,而支持向量机本身又能很好地解决弹药消耗的非线性问题。本文首先分析航空弹药训练消耗影响因素;其次利用邻域粗糙集的变量选择方法对影响航空弹药消耗的影响因素进行属性约简,筛选出一些有代表性的影响因素;然后对这些有代表性的变量进行支持向量机学习,获得预测值;最后与传统支持向量机预测模型以及双隐含层BP神经网络预测模型(一种深度学习算法)比较预测误差,以期获得更好的预测性能。
1 NRS-SVM模型根据航空弹药的一般消耗规律可知,航空弹药的训练消耗一般受弹药的训练需求量和供给量影响。其中训练消耗量由训练强度大小(包括训练次数和训练天数)以及训练规模大小(出动飞机架次和参与训练人数)量化得出,弹药的供给主要由现有弹药储备量决定。而这些自变量会受到国际局势、地缘政治以及国家发展战略等宏观因素影响,往往呈现出非线性发展的态势,因此运用一般的多元线性回归很难解决航空弹药训练消耗预测问题,本文提出用非线性支持向量机模型来对航空弹药训练消耗进行回归预测。同时,为了减轻支持向量机学习与预测的负担,使用邻域粗糙集对原始数据进行属性约简,通过消除冗余信息进而提高支持向量机预测的精度,以期获得更好的预测性能。基于此,参考赛英等[11]和李楠[17]的研究,本文构建基于邻域粗糙集与支持向量机融合的航空弹药训练消耗预测模型,其建模思路如图 1所示。

|
图 1 基于NRS-SVM的航空弹药预测模型 Figure 1 Aviation ammunition prediction model based on NRS-SVM |
1.1 邻域粗糙集属性约简
对于一个邻域决策系统DS=(U, A, V, f),U= {x1, x2, …, xn}为论域,也就是研究对象的全体,n表示论域中的样本个数,本文的样本数据为支持向量机的训练集数据,包括1991年至2010年共20年的数据,也即n=20;A=C∪D表示属性集合{a1, a2, …, am},其中C为条件属性,包括训练次数、训练天数、出动飞机架次、参与训练人数和弹药储备量,D表示决策属性,为弹药消耗指数,m表示数据集的属性数且m=6;V为各属性值Va的集合,
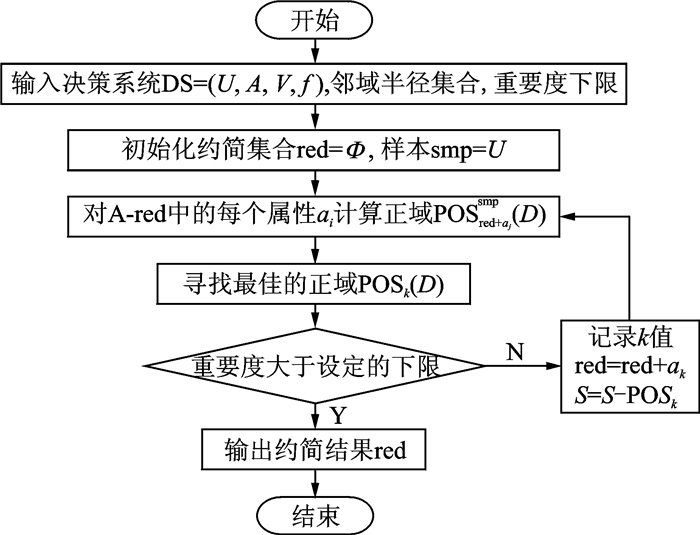
在决策系统中,有些条件属性对决策属性的影响起到了关键作用,认为这些属性比较重要。而有些条件属性的作用很小或没有什么作用,则认为这些属性是冗余的。因此根据条件属性对决策属性的影响程度定义属性重要性如下:在邻域决策系统DS=(U, A, V, f)中,对于∀B⊆C,若属性a∈B,则条件属性a对于决策属性D的重要性定义为Sig(a, B, D)=γB(D)-γB-{a}(D),其中γB(D)表示决策属性D对条件属性子集B的依赖度。且有γB(D)=|PosB(D)| / |U|,其中PosB(D)为条件属性子集B所确定的正域集合。属性重要性反映了条件属性对决策属性的贡献程度,属性重要性取值在0和1之间,属性重要性越大表明属性越重要,而当属性重要性为0时则表明该属性为冗余属性。若条件属性子集B满足PosB(D)=PosC(D)且Sig(a, B, D)>0,则表明条件属性子集B是条件属性集C的一个相对约简。邻域粗糙集属性约简就是将冗余的属性删除但又不影响决策系统本身的决策能力,其约简方法使用的是前向贪心算法,主要算法模型如图 2所示。
|
图 2 前向贪心算法 Figure 2 Forward greedy algorithm |
1.2 支持向量机回归与预测
通过邻域粗糙集属性约简将条件属性C约简为{a1, a2, …,al},其中l < m。在线性可分支持向量机原理基础上,通过引入核函数K(xi, xj)=(φ(xi), φ(xj))将数据映射到高维空间,进而建立非线性支持向量机模型进行回归和预测,具体算法如下:
(1) 给定训练集T={(x1, y1), (x2, y2), …,(xl, yl)}∈(Rn×y)l,其中xi∈ Rn为自变量数据集,yi∈y为因变量数据集。
(2) 在线性可分支持向量机原理基础上,引入Lagrange乘子,选择通用的高斯核函数,把非线性可分支持向量机回归模型的求解转化为构造和求解如下凸二次规划问题
| $ \begin{gathered} \mathop {\max }\limits_\alpha = \sum\limits_{i = 1}^l {{\alpha _i} - \frac{1}{2}\sum\limits_{i,j = 1}^l {{\alpha _i}{\alpha _i}{y_i}{y_j}\left( {\varphi \left( {{x_i}} \right),\varphi \left( {{x_j}} \right)} \right)} } \hfill \\ 0 \leqslant \alpha \leqslant C,\;\;\;\;i = 1,2, \cdots ,l \hfill \\ {\text{s}}{\text{.t}}.\;\;\;\;\sum\limits_{i = 1}^l {{\alpha _i}{y_i} = 0} \hfill \\ \end{gathered} $ | (1) |
式中:C表示惩罚参数;φ(x)为高斯核函数且φ(x)=eγ‖x-y‖2,γ为核参数。
(3) 在上述模型的基础上基于常用的粒子群算法(Particle swarm optimization,PSO)通过参数寻优找到最优的惩罚参数C和核参数γ,以使得回归模型对于训练集数据的误差最小。
(4) 基于最优的惩罚参数C和核参数γ得到最终的决策函数y=g(x),通过相关属性值的输入就能得到相应的预测值。
2 实证分析 2.1 数据预处理本文收集1991年至2015年某部队航空弹药训练消耗影响因素及弹药消耗指数相关数据,自变量包括训练次数、训练天数、出动飞机架次、参与训练人数以及弹药储备量,因变量为弹药消耗指数。航空弹药的消耗数据采用交叉选择数据集合进行训练与测试,前20年数据中奇数年的数据作为训练集数据,偶数年的数据作为测试集数据,以增加训练模型的趋势性增长的适应性,进而得到最优参数下的训练模型,然后对后5年的消耗数据进行预测。
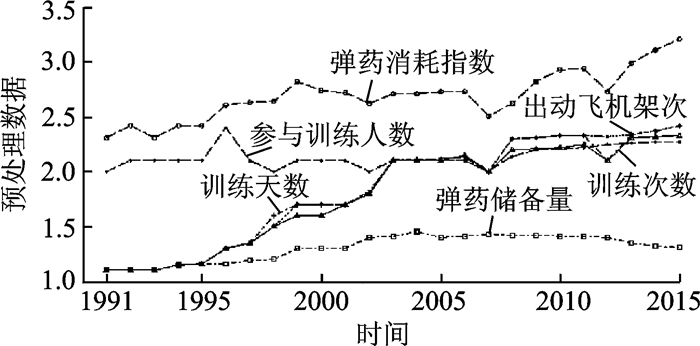
由于数据的敏感性及保密性要求,本文收集的数据以1990年数据为基准进行预处理,结果如图 3所示。图中横坐标为对应年份,纵坐标依次为训练次数、训练天数、出动飞机架次、参与训练人数、弹药储备量以及弹药消耗指数相对于以1990年基准数据首项归一化后的对应结果。由图 3可知,各个自变量与因变量之间并不是简单的线性关系,因此选择非线性支持向量机模型来进行预测具有一定的可行性。
|
图 3 某部队航空弹药训练消耗预处理数据 Figure 3 Aviation ammunition training consumption pretreatment data for a certain unit |
2.2 邻域粗糙集属性约简
首先对前20年训练集数据进行邻域粗糙集属性约简。对于一个邻域决策系统DS=(U, A, V, f),U={x1, x2, …,x20}为论域,属性集合A= {a1, a2, …,a6},其中条件属性C= {a1, a2, a3, a4, a5},分别表示训练次数a1、训练天数a2、出动飞机架次a3、参与训练人数a4、弹药储备量a5,决策属性D={a6}为弹药消耗指数a6,基于MATLAB软件对训练集数据进行属性约简,将属性重要度低于0.1的条件属性进行约简,最终得到约简后属性及相应属性重要度如表 1所示。
| 表 1 邻域粗糙集属性约简结果 Table 1 Neighborhood rough set attribute reduction results |
由表 1可知,条件属性(出动飞机架次a3和参与训练人数a4)属于冗余属性被约简掉,约简后的属性包括训练天数a2、弹药储备量a5和训练次数a1,且属性重要度依次提高,这表明条件属性中训练天数、弹药储备量和训练次数对于决策属性弹药消耗指数的影响起到了关键作用,且训练次数作用最大,而相比之下条件属性中出动飞机架次和参与训练人数的作用很小或没有什么作用,认为这些属性是冗余的。因此通过邻域粗糙集对这两个属性进行约简。
2.3 支持向量机回归与预测依据约简后的数据建立训练集T= {(x1, y1), (x2, y2), …,(x20, y20)} ∈(Rn×y)l,其中xi= {xi1, xi2, xi3}分别为训练天数、弹药储备量和训练次数,输出yi为弹药消耗指数。同时建立测试集 T={(x21, y21), (x22, y22), …, (x25, y25)}∈ (Rn×y)l。
采用交叉选择数据集合进行支持向量机的回归,前20年数据中奇数年的数据作为训练集数据,偶数年的数据作为测试集数据,基于粒子群算法运用MATLAB软件进行参数寻优,其中C∈(0.1, 1 000),γ∈(0.01, 1 000),进而得到最优参数下的训练模型,其中最优惩罚参数C=613和核参数γ=0.01,以使得回归模型对于训练集数据的误差最小,且最小均方误差为0.057 7。
最后基于MATLAB程序对后5年数据进行预测,得到最终的预测值yi={3.736 0, 3.505 6, 3.708 8, 3.714 3, 3.751 6}。
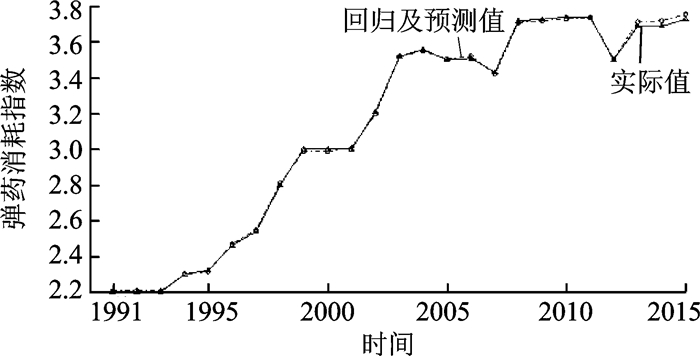
由此,通过NRS-SVM模型计算得到某部队航空弹药训练消耗1991年至2010年的回归值以及2011年至2015年的预测值,结果如图 4所示。由图 4可知,NRS-SVM模型所得结果相对误差很小,可以很好反映该部队航空弹药训练消耗情况。
|
图 4 某部队航空弹药训练消耗走势图 Figure 4 Aviation ammunition training consumption chart of a certain unit |
2.4 NRS-SVM模型与传统预测模型比较
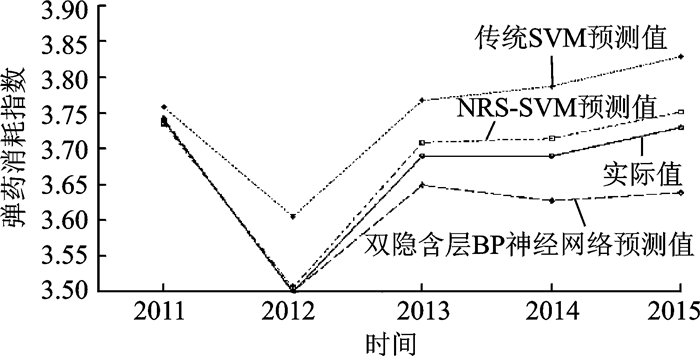
本文构建了基于邻域粗糙集与支持向量机融合的NRS-SVM模型,但与传统的SVM预测模型相比,NRS-SVM组合预测模型是否能够有效提高模型预测精度还有待进一步检验。基于此,本文重新构造训练集和测试集,其中训练集的自变量xi={ xi1, xi2, xi3, xi4, xi5},分别为训练次数、训练天数、出动飞机架次、参与训练人数和弹药储备量,同时输出yi为弹药消耗指数,通过粒子群算法得到最优惩罚参数C=22和核参数γ=0.01,进而得到最终的预测值,最后预测结果如表 2所示。此外,考虑到深度学习(多层神经网络)也在预测领域有广泛应用,因此本文参考Wan等[18]、杨金宝等[19]的研究,采用双隐含层BP神经网络模型对本文相关数据进行学习和预测,设置网络迭代次数epochs为10 000次, 期望误差goal为0.00001, 学习速率为0.01, 通过训练网络最终也得到预测值。最后的预测结果与NRS-SVM方法比较如图 5所示,其具体预测数值如表 2所示。由此可知,NRS-SVM组合预测模型的均方误差最小,故NRS-SVM组合预测模型相比于其他预测模型,其预测精度得到了显著提高,具有更好的预测性能。
| 表 2 不同预测模型预测结果 Table 2 Prediction results of different prediction models |
|
图 5 不同预测模型预测值比较图 Figure 5 Comparison of predicted values of different prediction models |
3 结束语
航空弹药消耗预测问题是航空弹药供应保障中的焦点和难点,本文结合航空弹药训练消耗的特点,提出基于邻域粗糙集与支持向量机融合的航空弹药训练消耗预测模型。NRS-SVM组合预测模型的优势在于通过邻域粗糙集属性约简技术提高支持向量机的预测性能,而支持向量机本身又能很好地解决弹药消耗的非线性问题。基于前向贪心算法通过邻域粗糙集将冗余属性约简得到航空弹药训练消耗的核心影响因素,在此基础上建立支持向量机回归模型,引入高斯核函数基于粒子群算法进行参数寻优得到最优惩罚参数和核参数,进而构建支持向量机预测模型。实证研究表明本文构造的NRS-SVM模型所得结果均方误差很小,可以很好反映航空弹药训练消耗情况,并且相比于传统SVM模型以及双隐含层BP神经网络预测模型(一种深度学习算法),其预测精度得到显著提高。因此本文构造的NRS-SVM组合预测模型相比于其他预测模型具有更好的预测性能。这为解决航空弹药训练消耗预测问题提供了有效的解决思路,不仅从理论层面丰富了弹药消耗预测领域的研究成果,而且对于切实提高航空弹药的供应保障效率具有积极的指导意义。
| [1] |
刘涛, 彭世蕤.
改进BP神经网络在航空弹药预测中的应用[J]. 探测与控制学报, 2009, 31(5): 52–55.
DOI:10.3969/j.issn.1008-1194.2009.05.012 LIU Tao, PENG Shirui. Application of improved BP neural network to prediction of aviation ammunition consumption[J]. Journal of Detection & Control, 2009, 31(5): 52–55. DOI:10.3969/j.issn.1008-1194.2009.05.012 |
| [2] |
陈利安, 肖明清, 程相东.
航空弹药平时消耗量预测模型对比[J]. 弹箭与制导学报, 2010, 30(3): 239–242.
DOI:10.3969/j.issn.1673-9728.2010.03.071 CHEN Lian, XIAO Mingqing, CHEN Xiangdong. Comparison of peacetime aviation ammunition consumption forecast models[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(3): 239–242. DOI:10.3969/j.issn.1673-9728.2010.03.071 |
| [3] |
陶茜, 彭力, 潘勃, 等.
基于蚁群算法的航空弹药需求测算[J]. 火力与指挥控制, 2010, 35(9): 34–37.
DOI:10.3969/j.issn.1002-0640.2010.09.010 TAO Qian, PENG Li, PAN Bo, et al. Research on the calculation of t he air ammunition's demand based on the ant colony clustering[J]. Fire Control & Command Control, 2010, 35(9): 34–37. DOI:10.3969/j.issn.1002-0640.2010.09.010 |
| [4] |
邱国斌.
基于战争视角的航空弹药消耗模型比较研究[J]. 西安航空学院学报, 2015, 33(5): 24–27.
DOI:10.3969/j.issn.1008-9233.2015.05.007 QIU Guobin. Comparative study on consumption models of aviation am munition from the perspective of war[J]. Journal of XIAN Aeronautical University, 2015, 33(5): 24–27. DOI:10.3969/j.issn.1008-9233.2015.05.007 |
| [5] |
康宗宇, 陈义军, 陈伟.
航空战时弹药保障供应能力优化预测仿真[J]. 计算机仿真, 2017, 34(2): 49–52.
DOI:10.3969/j.issn.1006-9348.2017.02.011 KANG Zongyu, CHEN Yijun, CHEN Wei. Simulation of aviation ammunition support supply capability optimization[J]. Computer Simulation, 2017, 34(2): 49–52. DOI:10.3969/j.issn.1006-9348.2017.02.011 |
| [6] |
孙云聪, 万华.
Elman和BP网络应用于航空训练弹药需求预测的对比研究[J]. 舰船电子工程, 2017, 37(3): 100–103.
DOI:10.3969/j.issn.1672-9730.2017.03.025 SUN Yuncong, WAN Hua. Comparative study on the application of Elman and BP neural network in aviation training ammunition requirement forecasting[J]. Ship Electronic Engineering, 2017, 37(3): 100–103. DOI:10.3969/j.issn.1672-9730.2017.03.025 |
| [7] |
周一鸣, 王茜, 杨硕.
动态灰色模型在航空弹药维修器材消耗规律中的应用[J]. 物流科技, 2017, 40(7): 135–137.
DOI:10.3969/j.issn.1002-3100.2017.07.038 ZHOU Yiming, WANG Qian, YANG Shuo. The application of dynamic gray forecast model on the consumption rule of aviation ammunition spares[J]. Logistics Sci-tech, 2017, 40(7): 135–137. DOI:10.3969/j.issn.1002-3100.2017.07.038 |
| [8] |
SINGH D, KHAN M A, BANSAL A, et al. An application of SVM in character re cogn ition with chain code[C]//Communication, Control and Intelligent Systems (CCI S).[S.l.]: IEEE, 2015: 167-171. |
| [9] |
MELLIT A, PAVAN A M, BENGHANEM M.
Least squares support vector machine for short-term prediction of meteorological time series[J]. Theoretical and Applied Climatology, 2013, 111(1/2): 297–307.
|
| [10] |
ZENG J, QIAO W.
Short-term solar power prediction using a support vector machine[J]. Renewable Energy, 2013, 52: 118–127.
DOI:10.1016/j.renene.2012.10.009
|
| [11] |
赛英, 张凤廷, 张涛.
基于支持向量机的中国股指期货回归预测研究[J]. 中国管理科学, 2013, 21(3): 35–39.
SAI Ying, ZHANG Fengting, ZHANG Tao. Research of Chinese stock index futures regression prediction based on support vector machines[J]. Chinese Journal of Management Science, 2013, 21(3): 35–39. |
| [12] |
VAPNIK V, IZMAILOV R.
Knowledge transfer in SVM and neural networks[J]. Annals of Mathematics and Artificial Intelligence, 2017, 81(1/2): 3–19.
|
| [13] |
LIU Y, WANG F, HU D, et al. Multi-feature fusion with SVM classification for crime scene investigation image retrieval[C]//Signal and Image Processing (ICSIP), 2017 IEEE 2nd International Conference on.[S.l.]: IEEE, 2017: 160-165. |
| [14] |
刘双印, 徐龙琴, 李道亮.
基于粗糙集融合支持向量机的水质预警模型[J]. 系统工程理论与实践, 2015, 35(6): 1617–1624.
LIU Shuangyin, XU Longqin, LI Daoliang. Water quality early-warning model based on support vector machine optimized by rough set algorithm[J]. Systems Engineering Theory & Practice, 2015, 35(6): 1617–1624. |
| [15] |
汪莹, 蒋高鹏.
RS-SVM组合模型下煤矿安全风险预测[J]. 中国矿业大学学报, 2017(2): 423–429.
WANG Ying, JIANG Gaopeng. Coal mine safety risk prediction by RS-S VM combined model[J]. Journal of China University of Mining & Technology, 2017(2): 423–429. |
| [16] |
孟宏鹏, 徐海燕, 宋遐淦.
基于粗糙集属性约简和支持向量机的变压器故障诊断[J]. 南京航空航天大学学报, 2017, 49(4): 504–510.
MENG Hongpeng, XU Haiyan, SONG Xiagan. Transformer fault diagnosis based on attribute reduction of rough set and SVM[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49(4): 504–510. |
| [17] |
李楠.基于邻域粗糙集的属性约简算法研究[D].西安: 陕西师范大学, 2011.
LI Nan. Study on feature selection based on neighborhood rough set[D]. Xi'an: Shaanxi Normal University, 2011.http://cdmd.cnki.com.cn/Article/CDMD-10718-1011142368.htm |
| [18] |
WAN D, XIAO Y, ZHANG P, et al. Hydrological big data predict ion based on similarity search and improved BP neural network[C]//Big Data Congress, 2015 IEEE International Congress on.[S.l.]: IEEE, 2015: 343-350.https://ieeexplore.ieee.org/document/7207242 |
| [19] |
杨金宝, 倪福生, 魏长赟, 等.
基于双隐含层BP神经网络的绞吸挖泥船产量预测[J]. 计算机与数字工程, 2016, 45(7): 1234–1237.
DOI:10.3969/j.issn.1672-9722.2016.07.009 YANG Jinbao, NI Fusheng, WEI Changyun, et al. Prediction of cutter -suction dredger production based on double hidden layer BP neural network[J]. Computer and Digital Engineering, 2016, 45(7): 1234–1237. DOI:10.3969/j.issn.1672-9722.2016.07.009 |
 2018, Vol. 50
2018, Vol. 50


