随着航空事业的蓬勃发展,国内空中交通流量不断增加导致终端区内进场航空器飞行情况更加复杂,给管制员的现场指挥带来了很大的压力。因此,对于历史航班雷达数据的分析显得格外重要。通过聚类分析提取出中心航迹,将中心航迹结果应用到改善终端区的进场程序管制中,可以用来改进并优化现有进离场飞行程序,减轻管制员的工作负荷;同时,对于同一航班航迹数据进行聚类分析,提取出中心航迹也对航空公司在未来制订飞行计划具有重要意义。国内外已经有许多学者对航迹历史数据进行了聚类分析, 首先对原始雷达数据进行转码处理,进而提取出航迹特征点[1-5]进行聚类分析;Gariel等[6]对雷达航迹进行了聚类,同时对航迹运行进行了实时监控;Rehm[7]直接利用现有航迹定义其相似性,对同一机场中不同跑道的进场程序进行聚类分析;王超等[8]根据对实际航迹数据特征进行分析,建立基于对应雷达航迹点逆向比对方法的航迹相似性测度模型,同时提出了管制适用性的评价指标;赵恩来等[9]提出一种改进的基于密度的航迹聚类算法,解决了雷达站观测数据的分类问题;王增福等[10]对距离、方位角等平面坐标数据进行了相关处理,同时也对雷达数据提出了基于减法聚类的自适应航迹聚类算法;王涛波、黄宝军[11]首先分析了广播式自动相关监视(Automatic dependent surveillance-broadcast, ADS-B)航迹数据的特点,对异常数据进行了相关处理,并使用模糊聚类法提取航迹特征点。
以上文献只将二维或三维航迹点进行了聚类,没有考虑时间信息。对于进场阶段,当航空器飞行到某一坐标点尤其是转弯点等特殊位置时,航迹的分布规律与时间有很大关系,必须将时间因素考虑在空间聚类中;同时,航空器的航向变化和进场速度也是表征航空器的运行规律的两个重要因素,两者的参数变化会影响航迹点的分布,从而得到不同的聚类效果;此外航迹点中存在着离群点,如果不将离群点剔除,得到的聚类结果是不准确的。本文首次提出基于LOFC(LOF outlier detection and clustering-based method, LOFC)时间窗分割算法,将LOF算法和基于时间窗分割的K均值聚类算法的优势结合在一起。在新算法中,首先应用LOF算法对离群点进行识别和剔除,再将航空器的航向变化以及进场平均速度作为分割时间窗内航迹点个数的影响因子,利用基于时间窗分割的K-means算法对进场航迹点聚类,通过仿真分析得出良好的聚类结果。
1 数据初始处理 1.1 原始二次雷达数据转码本文要处理的数据源是原始二次雷达数据,首先对原始二次雷达数据进行解码转换成全文本明码类型,然后再将所有含有有用信息的文本条目按关键字逐一捡出,并将所需字段转换成程序需要的二进制整数或浮点数格式,数据单位保留不变,最后整理得到的规范航迹数据形式如表 1所示。
| 表 1 整理得到的二次雷达数据 Table 1 Data collected from secondary radar |
1.2 UTM投影方式
由于二次雷达返回的是经纬度信息,只有转换成大地坐标才能准确地反映出飞机的实际运行轨迹,以机场的导航台为坐标原点,建立直角坐标系。通过斜墨卡托投影将返回航迹的经纬度数据转换为大地坐标,采用matlab自带函数UTM进行转化。坐标转换得到直角坐标系下的横纵坐标(单位为千米)如表 2所示。
| 表 2 经纬度坐标转换成平面坐标 Table 2 Converte coordinates of longitude and latitude into plane coordinates |
2 LOFC时间窗分割算法 2.1 离群点识别和剔除
首先对航迹点中的离群点进行识别和剔除,计算出每个航迹点所对应的LOF值。航迹点中的LOF值越接近1,说明p的密度与其邻域点的密度差不多,p可能和邻域同属一簇;如果这个比值越小于1,说明p的密度高于其邻域点密度,p为密集点;如果这个比值越大于1,说明p的密度小于其邻域点密度,p越可能是异常点。
2.2 基于时间窗分割的K-均值聚类算法由于航空器飞行到某个坐标点,尤其是进场时往往与时间有较大关系,因此本文将航空器的飞行看作一个过程,也即航迹点的分布是一个与时间t相关的函数,对某一航段的航空器,建立时间窗。考虑表 1中所示雷达数据接收时间间隔为4s,同时为了避免出现选取的时间窗过小使得单位时间窗内航迹点数目过少的问题,本文取1min为单位,对同一航路上的航迹点进行时间窗分割。根据航迹空间分布特点,首先对航迹点进行特征提取,然后采取K-means聚类算法对分割好的时间窗内的航迹点进行聚类分析。
2.2.1 航迹点特征提取对表 1中的航向和速度指标进行提取,建立模型。
每架航空器的航迹数据由一系列离散的航迹点组成。设进场时间为TJ,某架进场航空器所对应的航迹序列为Lk,Lk={ s1, s2, …, sn},其中,k为各架航空器对应的呼号,n为Lk所对应的航迹点的个数,每个航迹点si都包含一个五维的向量,si=(ti, xi, yi, zi, vi),其中ti代表航迹点si对应的时刻,xi代表航迹点si对应的横坐标,yi代表航迹点si对应的纵坐标,zi代表航迹点si对应的飞行高度,vi代表航迹点si对应的速度。对于进场航班信息中,平均速度和航向变化是反应航空器运行规律以及刻画航迹特征的两个重要指标。首先对航迹点中的平均速度和航向变化两大特征进行提取分析,建立参数:进场平均速度比率v、航向变化率
| $ r = \sqrt {\alpha \times {{\overline v }^2} + \left( {1 - \alpha } \right){{\left( {\frac{{\Delta h}}{h}} \right)}^2}} \;\;\;\;0 \leqslant \alpha \leqslant 1 $ | (1) |
构建权重因子矩阵g,对每列因子求和,得到矩阵w
| $ \mathit{\boldsymbol{g = }}\left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{21}}}& \cdots &{{r_{1n}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}} \\ \vdots&\vdots&\vdots&\vdots \\ {{r_{n1}}}&{{r_{n1}}}& \cdots &{{r_{nn}}} \end{array}} \right] $ | (2) |
| $ \mathit{\boldsymbol{w = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{w}}_1}} \\ {{\mathit{\boldsymbol{w}}_2}} \\ \vdots \\ {{\mathit{\boldsymbol{w}}_n}} \end{array}} \right] $ | (3) |
式中:
故单位时间窗内航迹点数
| $ {f_i} = {\text{round}}\left( {{\mathit{\boldsymbol{L}}_j} \times {N_{{\text{LOF}}}}} \right) $ | (4) |
式中NLOF表示剔除离群点后的航迹点总个数。
2.2.2 聚类分析及曲线拟合对第m个时间窗Tm内的航迹点:
(1) 从时间窗内的航迹点中随机选取一个点作为初始的聚类中心,Cm(xcm, ycm, zcm)。
(2) 计算各点与中心的距离
| $ \begin{array} [c]{l} {d_{{c_m}f}} = \hfill \\ \sqrt {{(x_{{c_m}}} - {x_f}{)^2} + {{\left( {{y_{{c_m}}} - {y_f}} \right)}^2} + {{\left( {{z_{{c_m}}} - {z_f}} \right)}^2}} \hfill \\ \end{array} $ | (5) |
(3) 不断重复计算第(2)步,直到聚类中心不再发生变化或者dm逐渐收敛满足要求为止。
得到聚类中心点后,使用样条曲线对聚类中心点进行连接,曲线在每个点处的一阶和二阶导数连续,具有连续、曲率变化均匀的特点,聚类得到的航迹满足飞行性能要求。
3 聚类效果评价为了评价航迹聚类效果,引入曲率概念,使用最小二乘法多项式对XY方向的曲线进行拟合。通过最小化误差的平方和寻找数据的最佳函数匹配,并使得这些求得的数据与实际数据之间误差的平方和为最小,将聚类航迹所得到的中心点数据拟合成函数表达式,再对函数求解曲率,求解出函数中曲率最小点所对应的曲率值,公式如下:
通过最小二乘法拟合出的函数表达式为:y=f(x)。设x,x+Δx是(a,b)内两个邻近的点,它们在曲线y=f(x)上对应的点为A,B, 并设对应于x的增量为Δx,弧s的增量为Δs。当Δx→0时,
| $ K = \frac{{\left| {y''} \right|}}{{{{\left( {1 + y{'^2}} \right)}^{3/2}}}} $ | (6) |
求解出函数曲线中曲率最小点所对应的曲率Kmin,Kmin值越小,代表函数曲线的光滑程度越好,从而说明聚类效果越好。
4 LOFC时间窗分割算法运算结果 4.1 仿真结果分析如图 1所示, 选取25条进场航迹,k=25,进场时间TJ=18 min,图中红色实心点代表航迹点,蓝色圆圈代表以航迹点为中心所画的实心圆,实心圆半径越大,代表离群程度越大。选取LOF等于1.00,即将LOF值大于1.00的对象归为离群点,将LOF小于1.00的对象视为正常数据,如图 2所示,从图中可以看出异常数据有8个,将异常数据进行剔除。对α从0.1到1.0开始每隔0.1取值,通过不同的α值分割航迹点,以α=0.4时的航迹为例,对航迹进行拟合得到表达式为

|
图 1 离群点识别及标注 Figure 1 Outlier recognition and annotation |

|
图 2 离群点对应LOF值 Figure 2 LOF values corresponding to outliers |
| $ \begin{gathered} f = \left( { - 0.002{\text{ }}69} \right){x^4} + \left( {1.547{\text{ }}4} \right){x^3} + \hfill \\ \left( { - 296.683{\text{ }}3} \right){x^2} + \left( {19{\text{ }}152.606{\text{ }}8} \right)x \hfill \\ \end{gathered} $ |
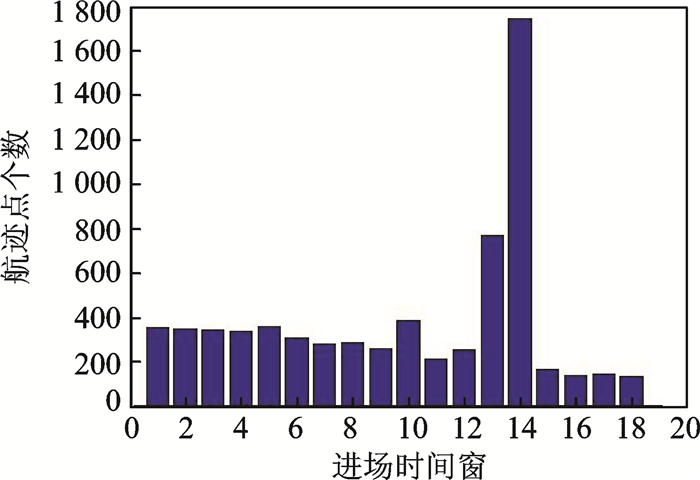
求得该航迹的最小曲率为0.099。同理,对其他α进行仿真得到影响因子α与航迹曲率值的关系,如图 3所示,从图中可以看出当α取0.7时,对应的航迹曲率值最小,光滑程度最佳,进而利用影响因子α=0.7时分割时间窗得到的航迹点与进场时间窗的关系如图 4所示。

|
图 3 影响因子与航迹曲率值的关系 Figure 3 Relationship between influence factor and flight path curvature |
|
图 4 利用影响因子分割时间窗得到的航迹点数 Figure 4 Track number obtained by segmentation of time window withinfluence factor |
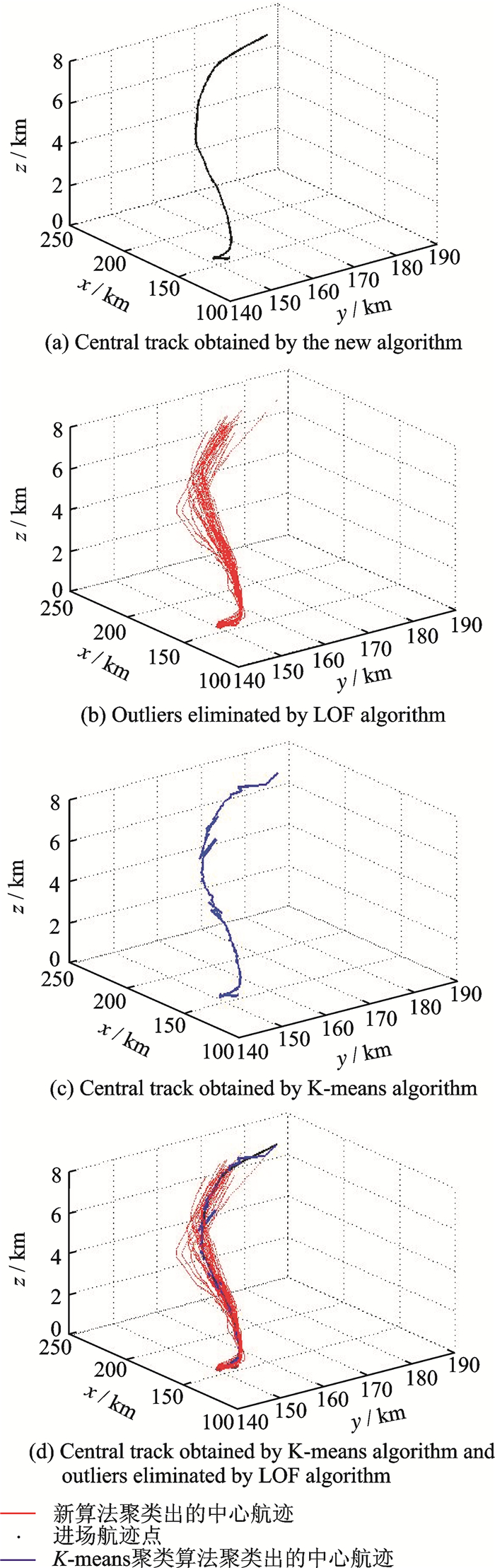
最后得到基于时间窗分割的LOFC算法的中心航迹如图 5所示。黑色实线代表新算法聚类得到的中心航迹,红色实心点代表进场经过LOF算法剔除掉离群点的航迹点,蓝色实线代表K-means算法聚类得到的中心航迹,从图中可以看出K-means算法得到的中心航迹有较多折线,与实际航迹有较大区别,而应用新算法得到的中心航迹特别是转弯点处更加光滑,更加符合航空器实际的运行规律。
|
图 5 聚类效果对比 Figure 5 Comparison of clustering results |
4.2 基于时间窗分割的LOFC算法优势
(1) 将时间因素考虑到聚类中,通过提取单位时间内航迹点影响因子划分时间窗,对每个时间窗内的数据进行聚类,得到三维聚类中心,使得各个聚类中心之间在时间上满足时间窗的间隔,从而使得聚类得到的航迹更加光滑,聚类效果更好。
(2) 将进场航空器平均速度和航向变化的因素考虑到航迹聚类中,建立两者的影响因子,用25条进场航迹的影响因子分割航迹点,影响因子越大,单位时间窗内分得的航迹点数目越多,避免了由于进场速度、航向变化过大,得到的聚类中心距离较大,最后仿真得到的中心航迹中折线过多等问题,使得拟合出的盛行交通流更加符合航空器实际的运行规律。
(3) 首次采用LOF算法对航迹中的离群点进行识别和剔除,避免了传统聚类算法把离群点和正常数据放在一起进行聚类、得到的聚类结果不准确的问题。
(4) 将不同的影响因子对应的得到的航迹曲线拟合成函数表达式,求解出函数曲线中曲率最小点所对应的曲率,从而对聚类效果进行科学评价。
5 结束语本文对进场二次雷达数据进行仿真分析,经历了原始二次雷达数据转码、有用信息行的提取、进场高度筛选、斜墨卡托坐标投影变换、航迹点距离计算,再到利用基于时间窗分割的LOFC算法对离群点识别和剔除并得到中心航迹等几个阶段。从仿真结果中可以看出,利用新算法得到的中心航迹更加光滑,更加符合航空器的实际运行,解决了传统聚类算法中出现的问题:(1)将离群点聚类到正常数据中得不到准确结果;(2)未将航空器进场时间序列和进场平均速度以及航向变化考虑到航迹聚类中,得到的中心航迹中含有较多折线,不能体现实际飞行过程。
| [1] |
郑乐, 隋东, 张军峰, 等.
基于转弯点聚类的航空器飞行轨迹分析[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(1): 139–143.
DOI:10.3963/j.issn.2095-3844.2015.01.032 ZHENG Le, SUI Dong, ZHANG Junfeng, et al. Flight path analysis of aircraft based on turning point clustering[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2015, 39(1): 139–143. DOI:10.3963/j.issn.2095-3844.2015.01.032 |
| [2] |
吴丹, 冯新喜.
多雷达多目标航迹起始算法研究[J]. 空军工程大学学报(自然科学版), 2006, 7(1): 16–19.
DOI:10.3969/j.issn.1009-3516.2006.01.006 WU Dan, FENG Xinxi. Research on multi radar multi-target track ini tiation algorithm[J]. Journal of Air Force Engineering University(Natural Sc ience Edition), 2006, 7(1): 16–19. DOI:10.3969/j.issn.1009-3516.2006.01.006 |
| [3] |
徐涛, 李永祥, 吕宗平.
基于航迹点法向距离的航迹聚类研究[J]. 系统工程与电子技术, 2015, 37(9): 2198–2204.
XU Tao, LI Yongxiang, LÜ Zongping. Research on track clustering based on normal distance of track point[J]. Journal of Systems Engineering and Electronics, 2015, 37(9): 2198–2204. |
| [4] |
吕宗平, 李永祥, 徐涛.
面向机场噪声预测的多噪声因素航迹聚类[J]. 计算机工程与设计, 2015(12): 3349–3354.
LÜ Zongping, LI Yongxiang, XU Tao. Multi-noise factor track clustering for airport noise prediction[J]. Computer Engineering and Design, 2015(12): 3349–3354. |
| [5] |
宫峰勋, 戴丽华, 马艳秋.
自适应选取聚类中心K-means航迹起始算法[J]. 哈尔滨工业大学学报, 2014, 46(5): 113–119.
GONG Fengxun, DAI Lihua, MA Yanqiu. K-means track initiation algorithm based on adaptive selection of clustering center[J]. Journal of Harbin Industrial University, 2014, 46(5): 113–119. |
| [6] |
GARIEL M, SRIVASTAVA A N, FERON E.
Trajectory clustering and an application to airspace monitoring[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1511–1524.
DOI:10.1109/TITS.2011.2160628
|
| [7] |
REHM F. Clustering of flight tracks: AIAA 2010-3412[R]. USA: AIAA, 2010. |
| [8] |
王超, 徐肖豪, 王飞.
基于航迹聚类的终端区进场程序管制适用性分析[J]. 南京航空航天大学学报, 2013, 45(1): 130–133.
DOI:10.3969/j.issn.1005-2615.2013.01.022 WANG Chao, XU Xiaohao, WANG Fei. Applicability analysis of terminal area approach program control based on track clustering[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(1): 130–133. DOI:10.3969/j.issn.1005-2615.2013.01.022 |
| [9] |
赵恩来, 郝文宁, 赵飞, 等.
改进的基于密度的航迹聚类算法[J]. 计算机工程, 2011, 37(9): 270–272.
DOI:10.3969/j.issn.1000-3428.2011.09.094 ZHAO Enlai, HAO Wenning, ZHAO Fei, et al. Improved density based track clustering algorithm[J]. Computer Engineering, 2011, 37(9): 270–272. DOI:10.3969/j.issn.1000-3428.2011.09.094 |
| [10] |
王增福, 潘泉, 郎林, 等.
基于减法聚类的动态航迹聚类算法[J]. 系统仿真学报, 2009, 21(16): 5240–5246.
WANG Zengfu, PAN Quan, LANG Lin, et al. Dynamic track clustering algorithm based on subtractive clustering[J]. Journal of System Simulation, 2009, 21(16): 5240–5246. |
| [11] |
王涛波, 黄宝军.
基于4D航迹的模糊聚类分析[J]. 交通信息与安全, 2013, 31(6): 38–42.
DOI:10.3963/j.issn.1674-4861.2013.06.008 WANG Taobo, HUANG Baojun. Fuzzy clustering analysis of track based on 4D[J]. Journal of Transportation Information and Security, 2013, 31(6): 38–42. DOI:10.3963/j.issn.1674-4861.2013.06.008 |
| [12] |
王茜, 刘书志.
基于密度的局部离群数据挖掘方法的改进[J]. 计算机应用研究, 2014, 31(6): 1693–1696.
DOI:10.3969/j.issn.1001-3695.2014.06.021 WANG Qian, LIU Shuzhi. Improvement of local outlier mining based on density[J]. Computer Application Research, 2014, 31(6): 1693–1696. DOI:10.3969/j.issn.1001-3695.2014.06.021 |
 2018, Vol. 50
2018, Vol. 50


