近年来,中国航空业发展迅猛,已经成为拉动国民经济增长的朝阳产业。高速增长的航空需求使得机场拥堵日益严重、航班计划鲁棒性降低,进而引发的航班延误问题成为困扰航空公司的难题。航空公司可以通过管理自身的运营资源(飞机/机组)来尽量保障航班运行的准时性,在有效利用其资源的同时考虑计划运行的弹性及可靠性[1]。传统的飞机排班问题通常以最小化航班运营成本、最大化飞机利用率以及航空公司收益等为目标,而对航班延误的考虑不足。越来越多学者注意到,在实际运营中由于天气原因、机场拥堵等导致的航班延误、机组误衔接,甚至航班取消,不但会导致成本增加,还使得原计划的效率降低[2]。牟德一等在经典机组配对模型的基础上,提出了机组延误概率的概念,并给出了相应的计算方法。结果表明,基于机组延误概率最小的机组配对模型可降低运营总成本[3]。蓝伯雄和张米将延误成本引入传统机组排班模型,考虑最小化各项任务成本及延误成本,提出了基于随机延误因素的机组排班规划模型,有效地提升了排班的鲁棒性[4]。盛政研究如何以概率分布的形式来表达航班延误,并确定了延误成本的计算方法,优化后的模型提高了飞机排班鲁棒性,同时降低航空公司运营成本[5]。
上述文献大多针对延误航班自身进行研究,而较少考虑延误的波及效应,即延误的航班/机组会对与其共享资源的后续航班造成影响,引起后续航班串延误。针对航班延误及其传播问题,国内外学者已有诸多研究。Shervin等利用延误程度、延误等级、延误深度等相应指标分析航班延误以及延误传播的影响程度,基于延误波及树模型,明确了飞机指派、机组配对和航班计划之间的关系[6]。Wu等指出延误经常在晚点的飞机和机组之间进行转移,因此应同时决策飞机航线问题和机组配对问题,利用迭代集成方法,在综合考虑飞机航线和机组配对的航班计划中,计算延误波及成本的最小值[7]。荣耀、王建东以飞机、驾驶员和乘务员机组等关键飞行资源为出发点,研究初始航班延误所引起的下游航班波及延误问题[8]。丁建立等、Wu等基于同一架飞机执飞连续航班的情形,运用贝叶斯网络模型分析连续航班的延误传播情况。分析表明延误时间的不确定性是逐渐增大,合理设置航班延误传递关键环节的过站时间可以减小延误传播的几率[9-10]。Wong和Tsai通过Cox回归分析研究航班延误波及,以阐述由于飞机重复利用所导致的延误传播[11]。
Cox比例风险回归分析模型(Cox’s proportional hazards regression model,Cox model)是一种生存分析统计方法,生存分析可以研究所观察对象的存在状态及生存时间与众多影响因素之间的关联程度,该方法已经在地面交通领域得到广泛应用[12]。对于航班延误传播问题,航班是否延误就是其存在状态,延误持续时间就是其生存时间。因此,本文提出了以飞机资源共享的航班串为基础的不同机组配对方案,即满足飞机和机组的技术条件限制情况下,机组和飞机在机场不同时刻进行分离。将贝叶斯方法应用于Cox回归模型,对航班延误进行生存分析,研究飞行(飞机、机组)资源分离时刻不同对后续航班延误传播程度的影响,并对航班计划鲁棒性进行评价。
1 研究理论与方法 1.1 贝叶斯网络贝叶斯网络(Bayesian network, BN)又称信度网络,是一个带有概率注释的有向无环图。节点代表随机变量,弧代表影响概率,弧的方向代表两个节点之间原因结果的影响关系。它以概率论为基础,研究客观事物中多个变量之间相互依赖的统计规律性。
贝叶斯网络的链式规则如下:假设U=(A1, A2, …, Ai)为贝叶斯网络变量集合,由贝叶斯网络确定的全部条件概率给出贝叶斯网络特定的联合概率分布
| $ \begin{array}{l} P\left( U \right) = \prod\limits_{i = 1}^n {P({A_i}|{A_1}, {A_2}, \ldots, {A_{i-1}})} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\prod\limits_{i = 1}^n {P({A_i}|pa({A_i}))} \end{array} $ | (1) |
式中pa(Ai)为贝叶斯网络中Ai的父节点的集合。P(U)反映了贝叶斯网络变量Ai与pa(Ai)之间的相关强度。本文在给定的航班串运行状态下对贝叶斯网络图中节点概率进行计算,反映延误沿着飞机和机组资源在航班串中的传播机理。
1.2 生存分析生存分析是对生存时间进行分析的统计技术的总称,它是用来研究对象的生存时间和结局与众多影响因素之间关系及其程度大小的方法。本文定义的“生存时间”是指从单个航班延误开始一直到延误结束的持续时间。对于离港航班而言,飞机的计划出发时刻标志着离港延误生存时间的开始,而飞机的实际出发时刻意味着生存时间的结束。可见,航班延误具有明显的生存特点。
传统的生存分析Cox回归法在研究某一因素与生存时间的关联时,该因素的取值或分类必须是恒定不变的[13]。而在航空运输中,影响航班延误的因素众多,且各因素对延误时间的影响效应也会随时间发生变化。因此,本文采用基于贝叶斯网络的Cox生存分析方法,可有效解决动态影响因素带来的不确定性问题[14],并且当有适当先验信息时,贝叶斯生存分析优于传统的生存分析方法[15, 16]。通过刻画各因素影响下的延误生存时间分布,探索不同时刻下资源分离对后续航班延误传播的影响程度。
确定生存函数是生存分析的关键。生存函数也被称为累积生存率,用一个非负随机变量T来表示生存时间,其定义为随机变量T超过时间点t的概率,其表达式为:S(t)=P(T>t)。当t=0时生存函数的取值为1,并且随着t逐渐增大,生存函数的取值逐渐减小。对于离港航班而言,生存函数的意义是航班延误时间T超过t时间(min)的概率。为了分析各影响因素(即协变量)对生存时间的影响,可以采用Cox回归分析的方法。
Cox回归模型的逻辑以风险函数表达,Cox风险函数的表达式为
| $ h\left( {t|\mathit{\boldsymbol{X}}} \right) = {h_0}\left( t \right){\rm{exp}}\left( {\mathit{\boldsymbol{\beta X}}} \right) $ | (2) |
式中:h0(t)是基准风险函数; X=(x1, x2, …, xp)T为已知的P维协变量向量,β=(β1, β2, …, βp)为回归系数向量,任何一个连续变量对应的系数βi均有明确的解释,表示变量xi每增加一个取值单位所发生的对数危险比。当x为连续变量时这样解释没有问题,但当x是多分类变量时只拟合一个回归系数就不合适。这种情况下,必须把原始的多分类变量转化为数个哑变量,每个哑变量只代表某两个或几个级别间的差异。
2 考虑资源分离时刻的航班串延误时间分析 2.1 资源分离方案由于延误因素随时间变化的影响效果不同,因而飞机与机组资源何时分离尤为关键。当航班发生到达延误,则分别共享飞机和机组资源的两个后续航班因等待飞机/机组资源而发生延误。国际航空运输协会的延误分类中,将这种延误称为“非周转型传播延误”(Non-rotational reactionary delay)[17], 并且延误将沿着共享资源的飞行航线不断波及到下游航班,形成波及延误航班串。因此,飞行资源的不适当分离使航班延误传播的程度更大,范围更广,涉及的航班量更多,延误成本更高。本文利用航空公司真实数据,建立两种带有飞行资源不同时刻分离的航班运行方案,通过对两种情景进行对比分析,说明资源分离对航班延误的影响。
以航空公司X提供的1年航班运行数据作为分析依据,选取某架飞机1天运营航班(含两组资源分离方案)的航班计划表(见表 1)。
| 表 1 案例学习航线及航班计划 Table 1 Case study of flight schedule |
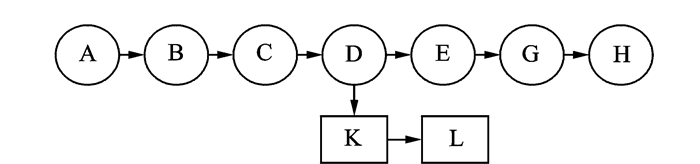
假设考虑两种不同时刻机组与飞机资源的分离方案,见图 1和图 2。其中圆形图标表示同一飞机执飞的航班串,方形图标表示机组和飞机分离后,同一机组执飞航班串。案例1中,在运行完航班B后,飞机与机组进行分离,飞机运行接下来的C-H6个航班,机组运行I, J航班;案例2中,在运行完航班D后,飞机与机组进行分离,飞机运行接下来的E-H四个航班,机组运行K, L航班。其中机组人员的排班情况满足相应的值勤期限制、飞行时间限制和休息要求等。

|
图 1 案例1资源分离方案 Figure 1 Resource separation scheme in Case 1 |
|
图 2 案例2资源分离方案 Figure 2 Resource separation scheme in Case 2 |
根据IATA延误编码方法,将延误原因分为7个主要类别,如表 2所示。对该公司航班运行数据统计发现,Reactionary因素中,由于乘客引起的延误占比很低,因此本文将“Non-rotational reactionary delay”视为Reactionary延误。
| 表 2 延误因素说明 Table 2 Delay factor explanation |
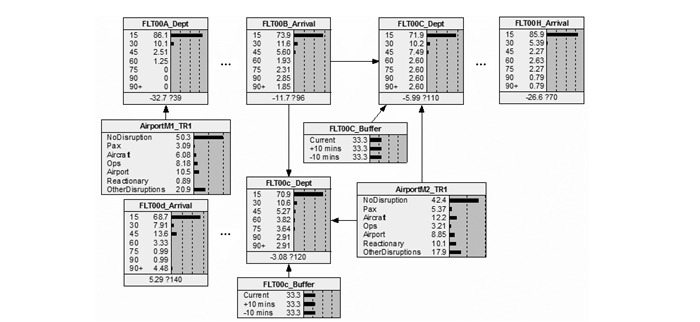
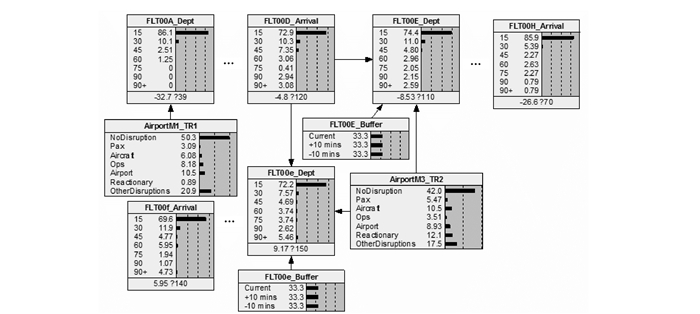
本文将进港/离港延误时间(min)分为[0,15],[15,30],[30,45],[45,60],[60,75],[75,90]和[90,∞]7个延误水平(规定延误15 min以内属于正常航班),构建案例1和案例2的贝叶斯网络图,如图 3,4所示。两种案例的飞机/机组资源分离机场均是M,因为分离时刻不同,所以分别表示为M2和M3,且M3的时间晚于M2。网络图从根节点开始,通过飞机和机组链接向后增加节点,显示延误在网络中波及的规模。
|
图 3 案例1贝叶斯网络图 Figure 3 Bayesian network in Case 1 |
|
图 4 案例2贝叶斯网络图 Figure 4 Bayesian network in Case 2 |
2.2 基于贝叶斯网络的延误因素影响分析
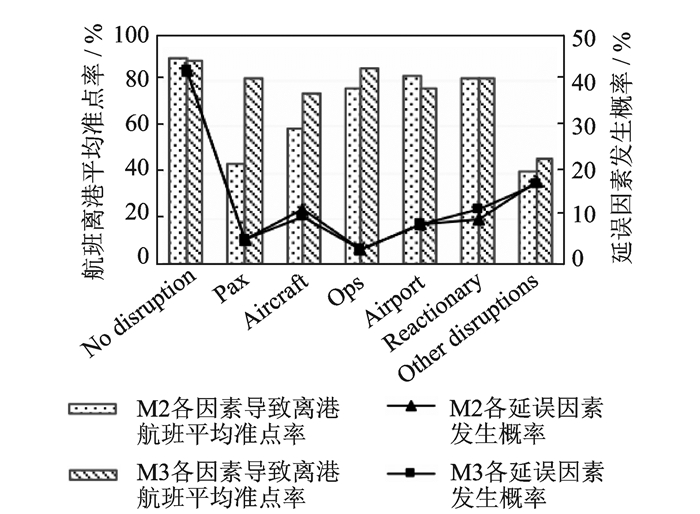
为分析各延误因素对航班离港延误的影响规律,本文将机组和飞机分离的机场M视为关键机场。对飞行资源在机场M2, M3分离后所运行的两个后续航班平均准点率进行分析,以评价不同时间段内各延误因素对航班准点率的影响见图 5。各延误因素对航班离港准点率的影响不尽相同,某些原因出现概率较低,但是对航班准点率的影响却极其严重。值得关注的是Pax,其发生的概率仅为5%,但一旦发生,M2机场的航班离港准点率将会降至43%。
|
图 5 M2, M3机场延误因素对离港准点率影响程度对比图 Figure 5 Comparison of delay factor on departure punctuality rate between airport M2 and M3 |
由图 5可发现,在机场不同时刻下,各延误因素的概率分布情况差异不大,但各延误因素对航班离港准点率的影响却存在差异。因此在选取飞行资源分离时刻时,应当充分考虑各延误因素的发生概率以及对航班准点率的影响。
为进一步分析不同时刻资源分离方案下延误因素对航班离港延误的影响,将航班离港延误程度分为[15,30],[30,45]和[45,60]3种不同延误水平,根据所建贝叶斯网络图推断各延误水平下延误因素的分布情况。
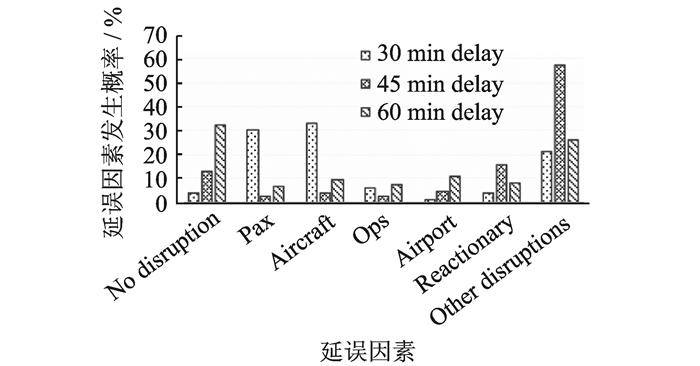
案例1情况下,当C, I航班处于不同延误水平时,推断的M2机场延误因素分布情况如图 6所示。当C, I航班都处于30 min延误水平时,Pax和Aircraft作为延误因素的发生概率均达到30%以上。当C, I航班处于45 min延误水平时,主要是由于Reactionary和Other disruptions导致,总共达到75%以上。当C, I航班离港延误都处于60 min延误水平时,5种主要延误因素导致延误的概率基本维持在10%,但是Other disruptions的作用相对明显。即同一时刻下,当离港航班处于不同的延误水平时,机场各延误因素的概率分布不相同。
|
图 6 案例1情景下的推断概率(C,I在机场M2离港) Figure 6 Inference probability in Case 1 scenario (C, I departing from airport M2 |
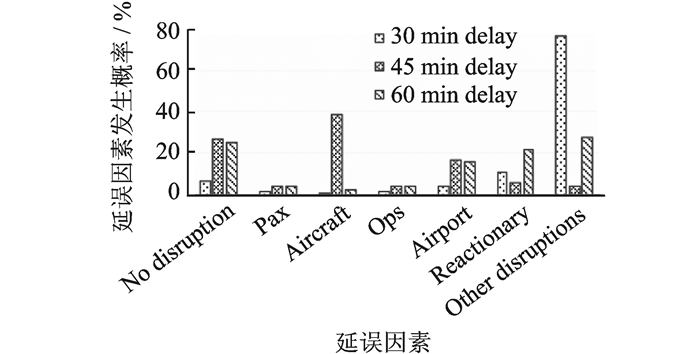
由图 7发现案例2情况下,E, K航班都在30 min延误水平时,主要由Other disruptions造成延误,其发生概率将近达到80%。当E, K航班都处于45 min延误水平时,主要是由于Aircraft和Airport导致延误,这两个延误因素发生概率之和接近60%。当E, K航班都处于60 min延误水平时,主要是由于Airport, Reactionary和Other disruptions导致延误,三者出现的概率总和达到60%。
|
图 7 案例2情景下的推断概率(E, K在机场M3离港 Figure 7 Inference probability in Case 2 scenario (E, K departing from airport M3) |
对比图 6, 7可看出,飞行资源分离(Reactionary因素)对航班延误水平有不同的影响,该因素更有可能出现于高延误水平航班(如延误时间为45~60 min航班)中;换言之,较长时间的航班延误,更有可能是Reactionary因素导致的。并且,资源分离时刻越晚,造成的延误时间越长。另一方面,同一延误因素对于不同资源分离情况下的航班延误影响效果不尽相同。即使离港航班处于相同延误水平,不同的出发时刻使得各因素对航班延误及其传播造成不同程度的影响。
2.3 基于Cox回归的延误时间累积分布由贝叶斯网络模型可知各延误因素对航班离港准点率的影响以及各延误因素的比例分配情况,但并不能得知各延误因素下航班延误持续时间的累积分布情况。因此本节进一步对离港延误航班进行生存分析,研究各延误因素对离港航班延误生存时间的影响。基于贝叶斯网络,对Cox比例风险模型中各类协变量给出先验性假设,分析各延误因素下的延误时间累积分布情况。
基于贝叶斯方法得到的延误因素概率分布,将延误原因种类作为协变量,航班离港延误时间作为观察结果,使用Cox比例风险模型分析延误时间累积分布,变量及其赋值见表 3。航班离港延误时间在各延误因素下的生存曲线见图 8。
| 表 3 影响航班离港延误的因素及其赋值 Table 3 Factors affecting flight departure delay and assignments |
|
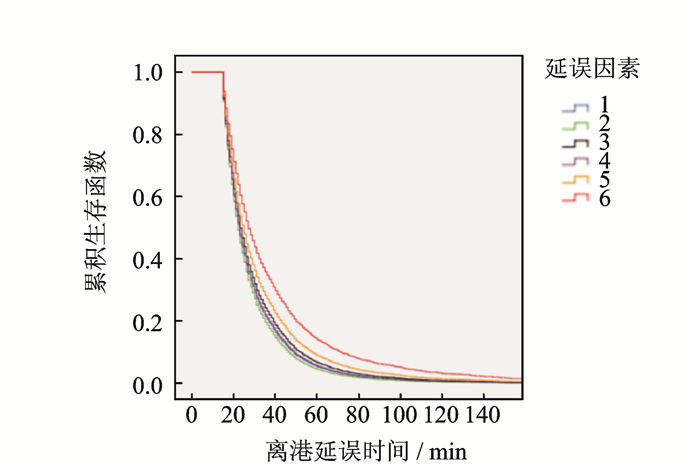
图 8 各延误因素生存曲线图 Figure 8 Survival curve of each delay factor |
航班离港延误时间在各延误因素下的生存曲线如图 8所示。由于生存函数的意义是生存时间大于时间点t的概率,对应到图 8中即各延误因素导致航班离港延误时间大于t min的概率。由图 8可见,各延误因素导致航班离港延误的时间60%以上集中在40 min以内。与另外4种延误因素相对比,Reactionary和Other disruptions这两种延误因素导致较长离港延误时间的概率较大,其他4种延误因素导致的航班离港延误时间相差无几。离港延误时间超过100 min的航班所占比例不足10%,除Reactionary和Other disruptions外,其他4种因素导致的延误时间基本控制在100 min以内。
案例1中进行资源分离的航班处于上午时段,案例2中进行资源分离的航班处于下午时段。为反映不同离港时刻下各延误因素对航班离港延误累积分布的影响,对在M机场离港的航班分上午(t≤11:00 am)、中午(11:00 am < t≤3:00 pm)以及下午(t>3:00 pm)3个时段。
当Cox回归分析中含有分类变量时,在分析时对这类自变量应采取数量化方法,即设置哑变量。对应文中提到的延误因素,共有6种不同的原因,则需要设置5个哑变量,将每种原因用1组哑变量的取值来表述,分类变量编码见表 4。在分析时,将第6种延误原因即Other disruptions作为参照组,各因素系数回归结果见表 5。a为分类变量表示延误因素种类;b为示性参数编码。
| 表 4 分类变量编码a Table 4 Classification variable coding a |
| 表 5 各因子回归结果 Table 5 Regression results of each factor |
表 5中,EXP(β)为各因素相对于对照因素Other disruptions发生航班离港的优势比。按照0.05的检验水准,在任何一个时间点上,这5种因素都比对照组因素导致航班继续延误的可能性小。对于上午离港的航班,由于Airport因素导致的延误航班结束延误的概率是Other disruptions的2.363倍,其他时间段下各延误因素的优势比解释相同。
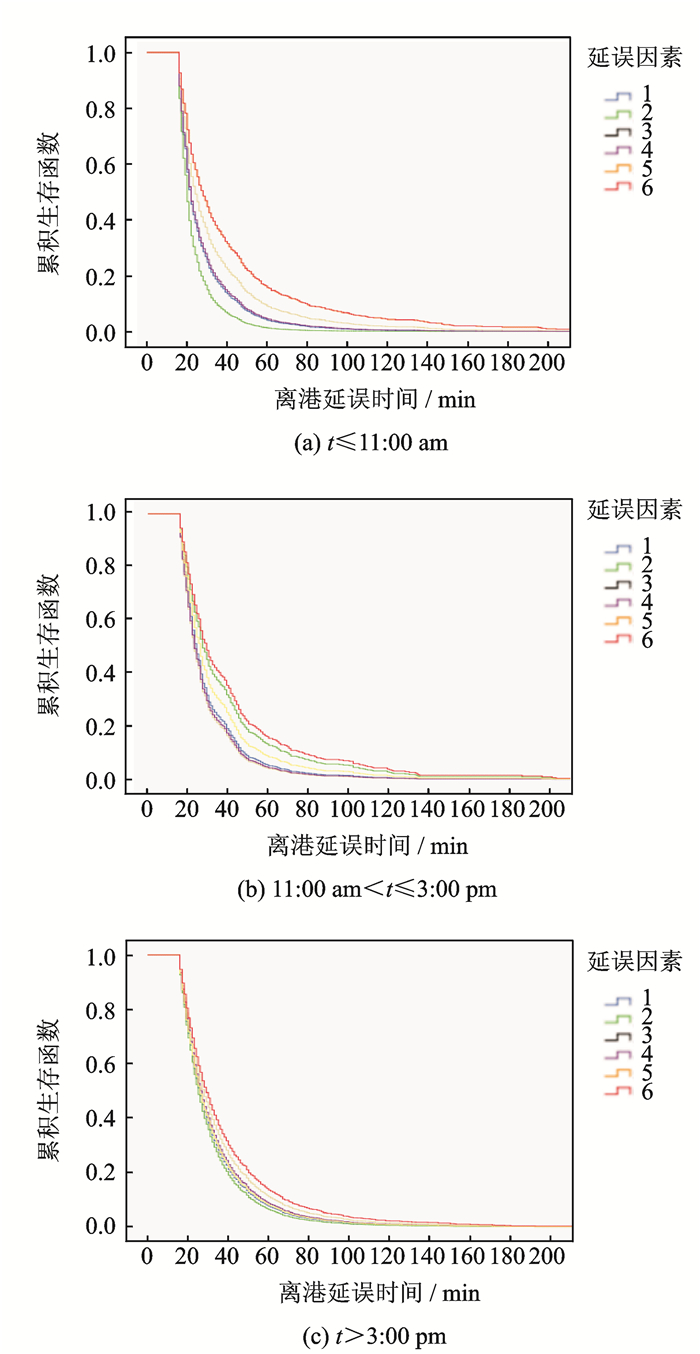
为直观看出各延误因素与对照组情况的差异,对模型结果进行图形观察,分别做出3个时段下航班离港延误的生存曲线图,见图 9(a-c),图中各条曲线分别表示各延误因素导致航班延误时间的生存曲线。显然,各曲线的生存率不同,也可看出3组生存函数在样本数据上存在差异。
|
图 9 不同时段航班离港延误生存曲线图 Figure 9 Delay survival curve of flight departure in different time periods |
在上午时段由于Airport因素导致的航班延误程度明显低于其他因素的影响程度,而在中午时段Airport因素的影响程度明显上升,航班离港延误时间超过40 min的航班比例由上午的不到10%上升至中午的30%左右。这是由于上午延误航班的累积导致机场起飞条件无法满足要求,如跑道的限制,空域的限制等。并且下午时段Airport原因仍易导致严重的离港延误。Aircraft, Ops, Pax这3个因素导致航班离港延误的生存曲线在3个时段基本保持一致,且变化不大。Reactionary和Other disruptions这两个因素导致航班离港延误的生存曲线在上午和下午两个时段的趋势也基本保持一致,且航班离港延误时间超过40 min的航班比例都超过30%,但在中午时段由于Reactionary造成的航班离港延误程度明显较低。由此可见,对于同一关键机场,选择不同时刻分离资源对其后续航班的延误波及程度尤为重要。相对于上午时段的航班,飞机在下午时段由于连续运行多个航班,累积的延误时间变长,机组或飞机不能及时供给,此时的资源分离势必导致后续航班延误时间加长,所受延误波及更严重。
3 运营鲁棒性分析航空公司航班计划的鲁棒性指航班计划具有一定的“抗干扰能力”,即航班计划具有一定的缓冲时间来对自身进行调节,从而降低航班延误的概率、缩短延误时间,或者提高不正常航班的恢复能力。由于不同时刻下,资源分离的抗干扰能力及其对后续航班的准点率或延误时间有不同影响,因此,考虑缓冲时间对带有资源分离排班计划的鲁棒性影响。
本文通过建立以下两点评价指标进行分析,反映不同资源分离方案的抗干扰能力:(1)延误时间或准点率在后续航班中的情况;(2)缓冲时间调整对飞机和机组延误的减少幅度。
为证明缓冲时间调整对后续航班准点率及延误波及情况的影响,可将资源分离前一起执行的最后一个航班视为关键航班,基于贝叶斯网络模型对两个案例中的关键航班B, D分别增加10 min缓冲时间,计算后续航班的准点率和平均延误时间。
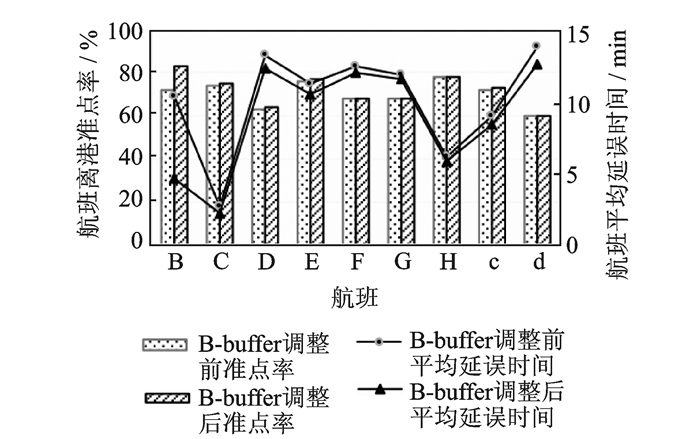
图 10为案例1情况下缓冲时间增加10 min前后准点率和延误时间的波及情况图,由图 10可看出航班B缓冲时间增加10 min对准点率的影响不大,平均延误时间的减少也不明显。
|
图 10 后续航班准点率及延误时间(案例1) Figure 10 Downstream flight departure punctuality rate and delay time (Case 1) |
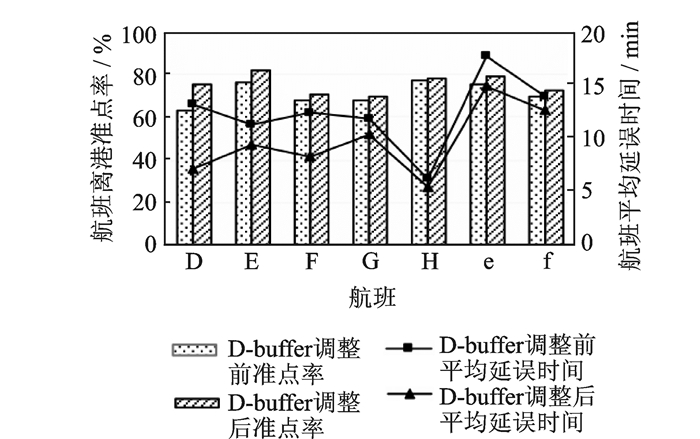
图 11为案例2情况下增加10 min缓冲时间准点率和延误时间的波及情况图,可见航班D缓冲时间增加10 min使得资源分离后飞机所执飞航线的E-H航班的准点率以及机组所执飞航线的K, L航班的准点率都得到一定提高,且后续航班平均延误时间减少幅度较大。通过以上分析可知对这两种资源分离方案下的关键航班分别进行同样的优化调整,即对关键航班B, D增加10 min缓冲时间,后续航班准点率改善程度不同。一般情况下越往后的航班缓冲时间调整对航班准点率的改进效果越不明显,这意味着若想提高下午航班的准点率,则需投入更多的缓冲时间。另一方面,在两种案例的机组资源共享航班串中(即I-J,K-L),方案1的总延误时间(21.06 min)小于方案2总延误时间(27.49 min)。由此可见,无论是从飞机利用率还是延误影响效果来看,选择方案1时刻进行资源分离,使沿着飞机资源和机组资源总的预期延误波及更小,航班计划的鲁棒性更强。
|
图 11 后续航班准点率及延误时间(案例2) Figure 11 Downstream flight departure punctuality rate and delay time (Case 2) |
4 结束语
本文通过案例学习的方法,利用基于贝叶斯网络的Cox回归模型,对带有飞行资源分离航班串中的延误波及情况进行研究。由于延误影响因素随时间变化具有不确定性,本文首先通过贝叶斯网络,分析各因素对航班延误水平的影响情况,并着重比较两种不同时刻资源分离情况下,reactionary因素对延误传播程度的影响。其次,基于Cox回归模型,对比分析资源分离时刻的不同对航班离港延误时间的累积分布情况。进而对不同时刻资源分离的航班计划提出优化调整方案及鲁棒性分析。结果表明,飞机资源与机组资源在不同时刻的分离对衔接航班的离港延误,以及整个后续航班串延误时间的影响都不同,因此航空公司在制定航班计划时需要考虑资源分离时刻对整个航班串抗外界干扰能力及运营鲁棒性的影响。
| [1] |
张海峰, 胡明华.
航空公司短期航班计划编排模型及算法[J]. 南京航空航天大学学报, 2015, 47(4): 553–558.
ZHANG Haifeng, HU Minghua. Planning model and algorithm for short-term flight scheduling of airline[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(4): 553–558. |
| [2] |
乐美龙, 马彬.
航班运控中飞机和机组快速整合优化恢复[J]. 南京航空航天大学学报, 2015, 47(4): 487–496.
LE Meilong, MA Bin. Aircraft and crew integrated fast optimal recovery in airline operation and control[J]. Journal of Nanjing University of Aeronautics Astronautics, 2015, 47(4): 487–496. |
| [3] |
牟德一, 王志新, 夏群.
基于机组延误概率的鲁棒性机组配对问题[J]. 系统管理学报, 2011, 20(2): 207–212.
MOU Deyi, WANG Zhixin, XIA Qun. Robust crew pairing problem based on probability of crew delay[J]. Journal of System & Management, 2011, 20(2): 207–212. |
| [4] |
蓝伯雄, 张米.
考虑延误因素的机组排班模型研究[J]. 中国管理科学, 2015, 23(12): 167–176.
LAN Boxiong, ZHANG Mi. Airline crew pairing model with stochastic disruption[J]. Chinese Journal of Management Science, 2015, 23(12): 167–176. |
| [5] |
盛政.基于延误成本的飞机排班鲁棒性问题研究[D].南京: 南京航空航天大学, 2015.
SHENG Zheng. The robust optimization design of aircraft assignment based on delay cost[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. |
| [6] |
SHERVIN A B, AMY C, YIHAN G, et al.
Analysis of the potential for delay propagation in passenger airline networks[J]. Journal of Air Transport Management, 2008, 14(5): 221–236.
DOI:10.1016/j.jairtraman.2008.04.010
|
| [7] |
WU C L, MICHELLE D, GARY F.
Robust airline schedule planning minimizing propagated delay in an integrated routing and crewing framework[J]. Transportation Science, 2012, 46(2): 204–216.
DOI:10.1287/trsc.1110.0395
|
| [8] |
荣耀, 王建东.
基于关键飞行资源的航班延误波及DAG模型的研究[J]. 小型微型计算机系统, 2009, 11(11): 2243–2247.
RONG Yao, WANG Jiandong. Research on flight delay propagation DAG based on critical flight resource[J]. Journal of Chinese Computer Systems, 2009, 11(11): 2243–2247. |
| [9] |
丁建立, 赵键涛, 曹卫东, 等.
基于动态贝叶斯网的航班延误传递分析[J]. 计算机工程与设计, 2015(12): 3311–3316.
DING Jianli, ZHAO Jiantao, CAO Weidong, et al. Analysis of flight delay transmit based on dynamic Bayesian network[J]. Computer Engineering and Design, 2015(12): 3311–3316. |
| [10] |
WU Weiwei, WU Chenglung.
Enhanced delay propagation tree model with bayesian network for modelling flight delay propagation[J]. Transportation Planning and Technology, 2018, 41(3): 1–17.
|
| [11] |
WONG J T, TSAI S C.
A survival model for flight delay propagation[J]. Journal of Air Transport Management, 2012, 23(7): 5–11.
|
| [12] |
GONG J, YANG W. The traffic bottleneck analysis on urban expressway under information condition[C]//The 2nd International Conference on Power Electronic and Intelligent Transportation System(PEITS). Shenzhen, China: [s.n.], 2009: 400-403. |
| [13] |
王文成, 杨小宝, 周映雪, 等.
基于Cox风险模型的城市道路交通拥堵持续时间分析[J]. 长安大学学报(自然科学版), 2015(S1): 235–239.
WANG Wencheng, YANG Xiaobao, ZHOU Yingxue, et al. Cox's proportional hazard regression model for estimating urban traffic congestion duration[J]. Journal of Chang'an University (Natural Science Edition), 2015(S1): 235–239. |
| [14] |
徐英, 骆福添.
生存分析中几种模型的研究概况[J]. 中国卫生统计, 2006, 23(4): 364–366.
DOI:10.3969/j.issn.1002-3674.2006.04.027 XU Ying, LUO Futian. A survey of several models in survival analysis[J]. Chinese Journal of Health Statistics, 2006, 23(4): 364–366. DOI:10.3969/j.issn.1002-3674.2006.04.027 |
| [15] |
肖媛媛, 许传志, 赵耐青.
常用生存分析模型及其对时依性协变量效应的估计方法[J]. 中国卫生统计, 2016, 33(3): 543–547.
XIAO Yuanyuan, XU Chuanzhi, ZHAO Naiqing. Common survival analysis model and estimation method for time dependent covariate effect[J]. Chinese Journal of Health Statistics, 2016, 33(3): 543–547. |
| [16] |
陈川.生存分析方法研究进展及其在心理学中的应用[D].广州: 华南师范大学, 2011.
CHEN Chuan. Research progress of survival analysis and its application in psychology[D]. Guangzhou: South China Normal University, 2011.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=J0014328 |
| [17] |
JETZKI M. The propagation of air transport delays in Europe[D]. Nordrhein-Westfalen, Germany: RWTH Aachen University, 2009. |
 2018, Vol. 50
2018, Vol. 50


