经典的多目标规划问题无论是在理论研究、求解方法,还是在应用研究方面都取得了重要进展。经典多目标规划大多解决的是确定环境下的决策问题,即经典多目标规划模型中的参数都是确定的[1, 2]。然而,实际规划问题涉及大量非确定因素。比如,多种突发情况下的飞机维修计划[3]、装备保障系统任务抢修时的各种冲突[4]等,这些因素一般是不确定的,称为非决定现象。实际生活中非决定现象大量存在,这使得经典多目标规划在应用中存在较大的局限性。人们逐渐发现在实际的生活中有一类可以得到观测数据的问题,这类问题通过充足的样本数据,利用概率统计的相关方法可以确定概率分布函数,可以使用概率论解决相应的问题。还有一类带有专家信度的问题[5],这种非决定的现象与随机现象不同,由于实践中无法获取足够的数据,只能借助专家去估计事件发生的信度。为了更好地解决这类带有专家信度的问题[6],Liu提出了基于不确定理论的不确定规划问题[6, 7]。然而,在现实系统中,既存在已知概率分布函数的随机变量,同时存在已知不确定分布的不确定变量,由此得到不确定随机变量。Liu[8]在2013年提出机会理论,用于处理这类既包括随机因素又包括不确定因素的问题,如不确定环境下存在多个任务点的无人机任务分配问题,由于战争的突发性、任务的时效性和战场的不透明性[9, 10],在进行无人机任务分配时无法得到足够的样本数据,影响其任务分配的非决定因素既包括不确定变量,也包括随机变量,如何在满足各种约束条件的前提下,使得无人机最短时间内,安全地遍历所有的任务点,完成作战任务是个典型的不确定随机问题[11-13]。多目标规划的“最优解”是不同意义下的有效解[13, 14],为了使模型的有效解更贴近实际问题的解决,需要对不同意义下的有效解进行更为全面的分析。期望值和方差都是不确定随机变量重要的数字特征[15-17],在实际求解中有广泛应用。
处理不确定随机多目标规划问题,可以建立不确定随机多目标规划模型(Uncertain random multi-objective programming problem, URMOP),通常情况下所建的模型中不确定随机变量往往是相互独立的,即变量独立的不确定随机多目标规划模型(Independent-uncertain random multiobjective programming problem, I-URMOP)。本文首先利用不确定随机变量之间的序关系定义URMOP问题的有效解,通过线性加权法把不确定随机多目标规划问题转化为不确定随机单目标规划问题,然后引入期望值方差准则,在期望值方差模型中把原问题转化为确定的单目标规划问题进行求解,最后通过无人机ISR任务分配问题证明求解得到的最优解是原问题的有效解。
1 模型建立I-URMOP指的是在各个目标函数中均含有独立不确定随机变量的多目标规划问题,该类问题可以通过如下的数学模型进行描述, 即
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{x \in {{\bf{R}}^n}} \left( {{f_1}\left( {x,{\xi _1}} \right),{f_2}\left( {x,{\xi _2}} \right), \cdots ,{f_p}\left( {x,{\xi _p}} \right)} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;{g_i}\left( {x,{\eta _i}} \right) \le 0,i = 1,2, \cdots ,m \end{array} \right. $ | (1) |
式中:x∈Rn为决策变量;ξ1, ξ2, …, ξp为定义在机会空间(Γ, L, M)×(Ω, A, Pr)上的相互独立的不确定随机变量;η1, η2, …, ηm为定义在机会空间(Γ, L,M)×(Ω, A, Pr)上的相互独立的不确定随机变量。
定义1[18] (Γ, L, M)表示的是不确定空间,(Ω, A, Pr)表示的是概率空间,那么两者的乘积空间(Γ, L, M)×(Ω, A, Pr)表示的是机会空间,在机会空间中定义机会测度为Ch[·]。
定义2[18] 不确定随机变量是从机会空间(Γ, L, M)×(Ω, A, Pr)到实数集的可测函数,同时随机变量是特殊的不确定随机变量,不确定变量也是特殊的不确定随机变量。
定义3 问题(1)的有效解是可行解x*,如果在数域中不存在可行解x使得
| $ \begin{array}{*{20}{c}} {{f_j}\left( {\bar x,{\xi _j}} \right) \le {f_j}\left( {{x^ * },{\xi _j}} \right)}&{j = 1,2, \cdots ,p} \end{array} $ | (2) |
成立,并且在数域至少存在一个j0, 1≤j0≤p,使得fj0(x, ξj)<fj(x*, ξj0)成立。
定义4 PEV准则指的是ξ和η是机会空间中两个不确定随机变量,当且仅当满足E[ξ]≤(< )E[η]且V[ξ]≤(< )V[η]的条件时,ξ≤(或<)η成立。其中,E[·], V[·]表示不确定随机变量的期望和方差。
定理1[18] 机会测度Ch[Θ]是Θ的单调函数且对于∀Λ∈L和B∈A,存在
| $ Ch\left\{ {\mathit{\Lambda } \times A} \right\} = M\left\{ \mathit{\Lambda } \right\} \times \Pr \left\{ B \right\} $ | (3) |
定理2[8] η1, η2, …, ηm表示独立的随机变量,其概率分布表示为Ψ1, Ψ2, …, Ψm,τ1, τ2, …, τn表示独立的不确定变量,不确定变量表示为
| $ \xi = f\left( {{\eta _1}, \cdots ,{\eta _m},{\tau _1}, \cdots ,{\tau _n}} \right) $ | (4) |
存在期望值
| $ \begin{array}{*{20}{c}} {E\left[ \xi \right] = \int_{{\mathit{\boldsymbol{R}}^m}} {\int_0^1 {f\left( {{y_1}, \cdots ,{y_m},\Upsilon _1^{ - 1}\left( \alpha \right), \cdots ,\Upsilon _n^{ - 1}\left( \alpha \right)} \right)} } }\\ {{\rm{d}}\alpha {\rm{d}}{\mathit{\Psi }_1}\left( {{y_1}} \right) \cdots {\rm{d}}{\mathit{\Psi }_m}\left( {{y_m}} \right)} \end{array} $ | (5) |
当且仅当f(η1, …, ηm, τ1, …, τn)对于不确定变量τ1, τ2, …, τn是单调函数。
定理3[8] η1和η2表示的是独立的随机变量,τ1和τ2表示的是独立的不确定变量,f1和f2是可测函数,函数fi(ηi, τi)表示的是不确定随机变量,那么
| $ \begin{array}{*{20}{c}} {E\left[ {{f_1}\left( {{\eta _1},{\tau _1}} \right) + {f_2}\left( {{\eta _2},{\tau _2}} \right)} \right] = }\\ {E\left[ {{f_1}\left( {{\eta _1},{\tau _1}} \right)} \right] + E\left[ {{f_2}\left( {{\eta _2},{\tau _2}} \right)} \right]} \end{array} $ | (6) |
成立。
定理4 机会分布函数α=Φ(x)是单调非降的,它的逆分布为
| $ x = {\mathit{\Phi }^{ - 1}}\left( \alpha \right) \buildrel \Delta \over = \mathit{\Phi }_1^{ - 1}\left( \alpha \right) = \inf \left\{ {x\left| {\mathit{\Phi }\left( x \right) \ge \alpha } \right.} \right\} $ | (7) |
| $ x = {\mathit{\Phi }^{ - 1}}\left( \alpha \right) \buildrel \Delta \over = \mathit{\Phi }_2^{ - 1}\left( \alpha \right) = \sup \left\{ {x\left| {\mathit{\Phi }\left( x \right) < \alpha } \right.} \right\} $ | (8) |
式中0≤α≤1。
证明:证明式(7)和式(8)等价。
任取x1∈{x|Φ(x)≥α},即Φ(x1)≥α,任取x2∈{x|Φ(x) < α},即Φ(x2) < α,那么,Φ(x1)>Φ(x2)。由Φ(x)的非降性可得,一定存在x1>x2,即{x|Φ(x)≥α}中的任意一个元素一定大于{x|Φ(x) < α}中的任意一个元素,那么Φ1-1(α)≥Φ2-1(α)。
下面利用反证法进一步证明。如果Φ1-1(α)>Φ2-1(α),那么一定存在x*使得Φ1-1(α)>x*>Φ2-1(α)。Φ2-1(α)是{x|Φ(x) < α}的上确界,所以x*∉{x|Φ(x) < α},可得x*∈{x|Φ(x)≥α}。但是Φ1-1(α)是{x|Φ(x)≥α}的下确界,应该存在x*≥Φ1-1(α),与前面结论矛盾,所以Φ1-1(α)>Φ2-1(α)不成立,两个定义等价。
2 模型求解求解多目标规划问题的思路是,构造一个可测度函数F把多目标问题转化成单目标问题,然后对问题进行求解,转化的结果为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{x \in {{\bf{R}}^n}} U\left( {x,\xi } \right) = \\ \;\;\;\;\;\;\;F\left( {{f_1}\left( {x,{\xi _1}} \right),{f_2}\left( {x,{\xi _2}} \right), \cdots ,{f_p}\left( {x,{\xi _p}} \right)} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;Ch\left\{ {{g_i}\left( {x,{\eta _i}} \right) \le 0} \right\} \ge {\alpha _i},i = 1,2, \cdots ,m \end{array} \right. $ | (9) |
U(x, ξ)表示一个不确定随机变量,在转化过程中保留了原问题的不确定随机性。
PEV准则下,问题(9)可以转化为确定性等价模型
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{x \in {{\bf{R}}^p}} E\left[ {U\left( {x,\xi } \right)} \right] + V\left[ {U\left( {x,\xi } \right)} \right] = \\ \;\;\;\;\;\;\;E\left[ {F\left( {{f_1}\left( {x,{\xi _1}} \right),{f_2}\left( {x,{\xi _2}} \right), \cdots ,{f_p}\left( {x,{\xi _p}} \right)} \right)} \right] + \\ \;\;\;\;\;\;\;V\left[ {F\left( {{f_1}\left( {x,{\xi _1}} \right),{f_2}\left( {x,{\xi _2}} \right), \cdots ,{f_p}\left( {x,{\xi _p}} \right)} \right)} \right]\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;\;Ch\left\{ {{g_i}\left( {x,{\eta _i}} \right) \le 0} \right\} \ge {\alpha _i},i = 1,2, \cdots ,m \end{array} \right. $ | (10) |
为了证明(10)的最优解同时是I-URMOP问题的有效解,根据PEV准则做以下证明。
定理5 ξ1, ξ2, …, ξn是服从正则机会分布Φ1, Φ2, …, Φn的独立不确定随机变量,如果函数f是严格单调增函数,那么
| $ \xi = f\left( {{\xi _1},{\xi _2}, \cdots ,{\xi _n}} \right) $ | (11) |
是不确定随机变量,同时具有逆分布
| $ {\mathit{\Psi }^{ - 1}}\left( \alpha \right) = f\left( {\mathit{\Phi }_1^{ - 1}\left( \alpha \right),\mathit{\Phi }_1^{ - 1}\left( \alpha \right), \cdots ,\mathit{\Phi }_n^{ - 1}\left( \alpha \right)} \right) $ | (12) |
证明:为了简单起见,本文以n=2为例进行证明。根据定义可得
| $ \left\{ {\xi \le {\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right\} \equiv \left\{ {f\left( {{\xi _1},{\xi _2}} \right) \le f\left( {\mathit{\Phi }_1^{ - 1}\left( \alpha \right),\mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right)} \right\} $ | (13) |
一方面,因为f是严格单调增函数,存在
| $ \left\{ {\xi \le {\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right\} \Leftrightarrow \left\{ {{\xi _1} \le \mathit{\Phi }_1^{ - 1}\left( \alpha \right)} \right\} \cap \left\{ {{\xi _2} \le \mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right\} $ | (14) |
因为变量ξ1, ξ2是独立的,所以
| $ \begin{array}{*{20}{c}} {Ch\left\{ {\xi \le {\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right\} \ge }\\ {Ch\left\{ {{\xi _1} \le \mathit{\Phi }_1^{ - 1}\left( \alpha \right)} \right\} \cap \left\{ {{\xi _2} \le \mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right\} = }\\ {Ch\left\{ {{\xi _1} \le \mathit{\Phi }_1^{ - 1}\left( \alpha \right)} \right\} \wedge Ch\left\{ {{\xi _2} \le \mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right\} = }\\ {\alpha \wedge \alpha = \alpha } \end{array} $ | (15) |
另一方面,因为f是严格单调增函数,存在
| $ \left\{ {\xi \le {\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right\} \Leftrightarrow \left\{ {{\xi _1} \le \mathit{\Phi }_1^{ - 1}\left( \alpha \right)} \right\} \cup \left\{ {{\xi _2} \le \mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right\} $ | (16) |
因为变量ξ1, ξ2是独立的,所以
| $ \begin{array}{*{20}{c}} {Ch\left\{ {\xi \le {\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right\} \ge }\\ {Ch\left\{ {{\xi _1} \le \mathit{\Phi }_1^{ - 1}\left( \alpha \right)} \right\} \cap \left\{ {{\xi _2} \le \mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right\} = }\\ {Ch\left\{ {{\xi _1} \le \mathit{\Phi }_1^{ - 1}\left( \alpha \right)} \right\} \vee Ch\left\{ {{\xi _2} \le \mathit{\Phi }_2^{ - 1}\left( \alpha \right)} \right\} = }\\ {\alpha \vee \alpha = \alpha } \end{array} $ | (17) |
Ch{ξ≤Ψ-1(α)}=α,因此Ψ-1是ξ机会分布的逆分布。
引理1 ξ和η是两个分别服从机会分布Φ和Ψ的不确定随机变量,对于
| $ E\left[ {a\xi + b\eta } \right] = aE\left[ \xi \right] + bE\left[ \eta \right] $ | (18) |
证明:
根据不确定随机变量的期望计算公式
| $ E\left[ \xi \right] = \int_0^1 {{\mathit{\Phi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } $ | (19) |
式中Φ-1(α)是ξ的逆分布。
由式(19)可得
| $ \begin{array}{*{20}{c}} {E\left[ {a\xi + b\eta } \right] = \int_0^1 {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } + \int_0^1 {b{\mathit{\Psi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } = }\\ {a\int_0^1 {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } + b\int_0^1 {{\mathit{\Psi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } }\\ {aE\left[ \xi \right] + bE\left[ \eta \right]} \end{array} $ | (20) |
引理得证。
引理2 ξ和η是两个分别服从机会分布Φ和Ψ的不确定随机变量,即
| $ V\left[ {a\xi + b\eta } \right] = {a^2}V\left[ \xi \right] + {b^2}V\left[ \eta \right] $ | (21) |
证明:
根据不确定随机变量的方差计算公式
| $ V\left[ \xi \right] = E\left[ {{{\left( {\xi - {e_\xi }} \right)}^2}} \right] = \int_0^1 {{{\left[ {{\mathit{\Phi }^{ - 1}}\left( \alpha \right) - {e_\xi }} \right]}^2}{\rm{d}}\alpha } $ | (22) |
式中eξ为ξ的期望。
因ξ和η相互独立,存在
| $ \begin{array}{*{20}{c}} {\int_0^1 {\left[ {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right) - a{e_\xi }} \right]} \cdot \left[ {b{\mathit{\Psi }^{ - 1}}\left( \alpha \right) - b{e_\eta }} \right]{\rm{d}}\alpha = }\\ {\int_0^1 {\left[ {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right) \cdot b{\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right]{\rm{d}}\alpha } + a{e_\xi } \cdot b{e_\eta } - }\\ {b{e_\eta } \cdot \int_0^1 {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha - a{e_\xi }} \cdot \int_0^1 {b{\mathit{\Psi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } = }\\ {ab\int_0^1 {\left[ {{\mathit{\Phi }^{ - 1}}\left( \alpha \right) \cdot {\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right]{\rm{d}}\alpha } + ab{e_\xi }{e_\eta } - }\\ {ab{e_\eta } \cdot \int_0^1 {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha - ab{e_\xi }} \cdot \int_0^1 {{\mathit{\Psi }^{ - 1}}\left( \alpha \right){\rm{d}}\alpha } = }\\ {ab{e_\xi }{e_\eta } - ab{e_\xi }{e_\eta } - ab{e_\xi }{e_\eta } + ab{e_\xi }{e_\eta } = 0} \end{array} $ | (23) |
| $ \begin{array}{l} V\left[ {a\xi + b\eta } \right] = \\ \begin{array}{*{20}{c}} {\int_0^1 {{{\left[ {\left( {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right) + b{\mathit{\Psi }^{ - 1}}\left( \alpha \right)} \right) - \left( {a{e_\xi } + b{e_\eta }} \right)} \right]}^2}{\rm{d}}\alpha } = }\\ {\int_0^1 {\left\{ {{{\left[ {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right) - a{e_\xi }} \right]}^2} + {{\left[ {b{\mathit{\Psi }^{ - 1}}\left( \alpha \right) - b{e_\eta }} \right]}^2}} \right\}{\rm{d}}\alpha } + }\\ {\int_0^1 {2\left[ {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right) - a{e_\xi }} \right] \cdot \left[ {b{\mathit{\Psi }^{ - 1}}\left( \alpha \right) - b{e_\eta }} \right]{\rm{d}}\alpha } = }\\ {\int_0^1 {\left\{ {{{\left[ {a{\mathit{\Phi }^{ - 1}}\left( \alpha \right) - a{e_\xi }} \right]}^2} + {{\left[ {b{\mathit{\Psi }^{ - 1}}\left( \alpha \right) - b{e_\eta }} \right]}^2}} \right\}{\rm{d}}\alpha } = }\\ {\int_0^1 {\left\{ {{a^2}{{\left[ {{\mathit{\Phi }^{ - 1}}\left( \alpha \right) - {e_\xi }} \right]}^2} + {b^2}{{\left[ {{\mathit{\Psi }^{ - 1}}\left( \alpha \right) - {e_\eta }} \right]}^2}} \right\}} }{\rm{d}}\alpha=\\ {{a^2}V\left[ \xi \right] + {b^2}V\left[ \eta \right]} \end{array} \end{array} $ | (24) |
引理得证。
引理3 ξ和η是两个分别服从机会分布Φ和Ψ的不确定随机变量。如果ξ≤(或<)η,那么,∀λ∈R+,λξ≤(或<)λη成立。
证明:因为ξ≤(或<)η有
| $ E\left[ \xi \right] \le \left( {或 < } \right)E\left[ \eta \right] $ | (25) |
| $ V\left[ \xi \right] \le \left( < \right)V\left[ \eta \right] $ | (26) |
| $ \lambda E\left[ \xi \right] \le \left( {或 < } \right)\lambda E\left[ \eta \right] $ | (27) |
| $ {\lambda ^2}V\left[ \xi \right] \le \left( < \right){\lambda ^2}V\left[ \eta \right] $ | (28) |
由引理1可得,对于任意λ∈R+,存在
| $ E\left( {\lambda \xi } \right) \le \left( < \right)E\left( {\lambda \eta } \right) $ | (29) |
| $ V\left( {\lambda \xi } \right) \le \left( < \right)V\left( {\lambda \eta } \right) $ | (30) |
即λξ≤(或<)λη成立。
引理得证。
引理4 假设, ξ1, ξ2是服从机会分布Φ1, Φ2的相互独立的不确定随机变量,η1, η2是分别服从机会分布Ψ1, Ψ2的相互独立的不确定随机变量。若ξ1≤η1, ξ2<η2或ξ1<η1, ξ2≤η2,有ξ1+ξ2<η1+η2。
证明:本文以ξ1≤η1, ξ2<η2为例进行证明,其他情况的证明方法与本文类似,由PEV准则可知,存在
| $ E\left[ {{\xi _1}} \right] \le E\left[ {{\eta _1}} \right],V\left( {{\xi _1}} \right) \le V\left( {{\eta _1}} \right) $ | (31) |
| $ E\left[ {{\xi _2}} \right] < E\left[ {{\eta _2}} \right],V\left( {{\xi _2}} \right) < V\left( {{\eta _2}} \right) $ | (32) |
根据式(30)和式(31)可得
| $ E\left[ {{\xi _1}} \right] + E\left[ {{\xi _2}} \right] < E\left[ {{\eta _1}} \right] + E\left[ {{\eta _2}} \right] $ | (33) |
根据引理1可得
| $ E\left[ {{\xi _1} + {\xi _2}} \right] = E\left[ {{\xi _1}} \right] + E\left[ {{\xi _2}} \right] $ | (34) |
| $ E\left[ {{\eta _1} + {\eta _2}} \right] = E\left[ {{\eta _1}} \right] + E\left[ {{\eta _2}} \right] $ | (35) |
综上可得,存在
| $ E\left[ {{\xi _1}} \right] + V\left[ {{\xi _2}} \right] < V\left[ {{\eta _1}} \right] + V\left[ {{\eta _2}} \right] $ | (36) |
根据式(31)和式(32)可得
| $ V\left[ {{\xi _1}} \right] + V\left[ {{\xi _2}} \right] < V\left[ {{\eta _1}} \right] + V\left[ {{\eta _2}} \right] $ | (37) |
根据引理2可得
| $ V\left[ {{\xi _1} + {\xi _2}} \right] = V\left[ {{\xi _1}} \right] + V\left[ {{\xi _2}} \right] $ | (38) |
| $ V\left[ {{\eta _1} + {\eta _2}} \right] = V\left[ {{\eta _1}} \right] + V\left[ {{\eta _2}} \right] $ | (39) |
综上可得,存在
| $ V\left[ {{\xi _1} + {\xi _2}} \right] > V\left[ {{\eta _1} + {\eta _2}} \right] $ | (40) |
即ξ1+ξ2<η1+η2成立。证毕。
线性加权法的求解思路是根据具体情况,将每一个不确定随机目标赋予相应的权值并进行线性加权求和,通过该方法转换得到的不确定单目标规划模型表示为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{x \in {{\bf{R}}^n}} U\left( {x,\xi } \right) = \sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {x,{\xi _i}} \right)} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;\mathit{Ch}\left\{ {{g_k}\left( {x,{\eta _k}} \right) \le 0} \right\} \ge {\alpha _k},k = 1,2, \cdots ,m \end{array} \right. $ | (41) |
其中
定理6 不确定随机单目标规划式(32)在PEV准则下的有效解是不确定随机多目标规划式(1)的PEV有效解。
证明:假设x*是不确定随机单目标规划(32)的最优解,但不是不确定随机多目标规划式(1)的PEV有效解,根据定义3可知,存在可行解x使得
| $ \begin{array}{*{20}{c}} {{f_i}\left( {\bar x,\xi } \right) \le {f_i}\left( {{x^ * },\xi } \right)}&{i = 1,2, \cdots ,p} \end{array} $ | (42) |
成立,并且至少存在某个i0, 1≤i0≤p,使得
| $ {f_{{i_0}}}\left( {\bar x,\xi } \right) < {f_{{i_0}}}\left( {{x^ * },\xi } \right) $ |
因为
| $ E\left[ {\sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {\bar x,\xi } \right)} } \right] < E\left[ {\sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {{x^ * },\xi } \right)} } \right] $ | (43) |
| $ V\left[ {\sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {\bar x,\xi } \right)} } \right] < V\left[ {\sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {{x^ * },\xi } \right)} } \right] $ | (44) |
即
| $ \sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {\bar x,\xi } \right)} < \sum\limits_{i = 1}^p {{\lambda _i}{f_i}\left( {{x^ * },\xi } \right)} $ | (45) |
于是
| $ U\left( {\bar x,\xi } \right) < U\left( {{x^ * },\xi } \right) $ | (46) |
根据定义3可知x*不是不确定随机单目标规划(51)的最优解,这与原本假设矛盾。因此原假设不成立,x*是不确定随机多目标规划(1)在PEV准则下的有效解。定理得证。
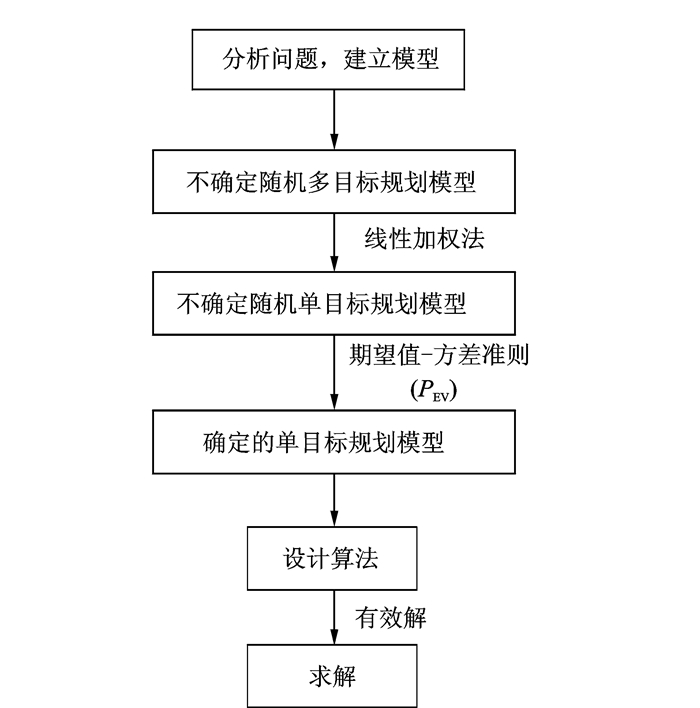
根据以上证明,可以总结不确定随机多目标规划问题求解流程如图 1所示。
|
图 1 不确定随机多目标规划求解流程图 Figure 1 Uncertain stochastic multi-objective programming solution flow chart |
3 案例分析
无人机情报侦察监视(Intelligence surveillance reconnaissance, ISR)[12]任务分配模型主要考虑3个决策目标,即无人机执行任务的时间(Time)、无人机执行任务受到的威胁(Threat)以及无人机执行任务的耗油量(Fuel)。目标函数主要受到敌方火力情况、复杂地形以及任务区域天气情况等3类不确定因素的影响,前两类由于敌方伪装等原因无法获取足量的数据,需要给出专家信度,可以设定为不确定空间(Γ, L, M)上的不确定变量,记为ξ1, ξ2;第3类可以结合气象卫星和历史数据,获取足量样本进行判断,可以设定为概率空间(Ω, A, Pr)上的随机变量,记为η。这3类不确定因素变量大多数情况下会同时对无人机执行任务的时间、无人机执行任务受到的威胁以及无人机执行任务的耗油量产生一定影响。此外,无人机执行ISR任务还会受到其他很多约束条件的限制,本文中主要考虑无人机执行ISR任务过程中的燃油约束条件,假设该型无人机的最大载油量是9 t, K表示任务位置点。综上所述,具体的无人机ISR任务分配模型为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{\pi \left( X \right)} \left( {{\rm{Time}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right),} \right.\\ \;\;\;\;\;\;\;{\rm{Threat}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right),\\ \;\;\;\;\;\;\;\;\left. {{\rm{Fuel}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right)} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;\;\;Ch\left\{ {{\rm{Fuel}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) - 9 \le 0} \right\} \ge 1 \end{array} \right. $ | (47) |
时间目标函数以350 km/h速度飞行时,受敌方火力和地形影响较大,以450 km/h速度飞行时,受天气影响较大,可以表示为
| $ \begin{array}{*{20}{c}} {{\rm{Time}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) = }\\ {\frac{{{\xi _1}}}{{{\xi _1} + {\xi _2}}}\left( {\sum\limits_{i = 1}^{n - 1} {\frac{{d\left( {{K_i},{K_{i + 1}}} \right)}}{{350}} + \frac{{d\left( {{K_n},{K_1}} \right)}}{{350}}} } \right) + }\\ {\eta \left( {\sum\limits_{i = 1}^{n - 1} {\frac{{d\left( {{K_i},{K_{i + 1}}} \right)}}{{450}} + \frac{{d\left( {{K_n},{K_1}} \right)}}{{450}}} } \right)} \end{array} $ | (48) |
威胁目标函数受敌方火力影响较大(系数为0.5),受天气和地形影响较小(系数为0.2),可以表示为
| $ \begin{array}{*{20}{c}} {{\rm{Threat}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) = }\\ {\ln \left( {{\xi _1}} \right)\left( {\sum\limits_{i = 1}^{n - 1} {\frac{{0.5}}{{d\left( {{K_i},{K_{i + 1}}} \right)}} + \frac{{0.5}}{{d\left( {{K_n},{K_1}} \right)}}} } \right) + }\\ {\frac{{\ln \left( {{\xi _2}} \right)}}{{{\eta ^2} + 1}}\left( {\sum\limits_{i = 1}^{n - 1} {\frac{{0.2}}{{d\left( {{K_i},{K_{i + 1}}} \right)}} + \frac{{0.2}}{{d\left( {{K_n},{K_1}} \right)}}} } \right)} \end{array} $ | (49) |
耗油量的目标函数相对比较复杂,本文中以式(50)表示为
| $ \begin{array}{*{20}{c}} {{\rm{Fuel}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) = 0.02 \times \frac{{\ln \left( {{\xi _1}} \right)}}{{\xi _2^2 + 0.3}} \times }\\ {\left( {\sum\limits_{i = 1}^{n - 1} {\left| {\ln {{\left( {\left( {d\left( {{K_i},{K_{i + 1}}} \right)} \right) - 45} \right)}^2}} \right|} + } \right.}\\ {\left. {\left| {\ln {{\left( {\left( {d\left( {{K_n},{K_1}} \right)} \right) - 45} \right)}^2}} \right|} \right) + 0.02 \times \ln \left( {\eta + 1} \right) \times }\\ {\left( {\sum\limits_{i = 1}^{n - 1} {\left| {\ln {{\left( {\left( {d\left( {{K_i},{K_{i + 1}}} \right)} \right) - 55} \right)}^2}} \right|} + } \right.}\\ {\left. {\left| {\ln {{\left( {\left( {d\left( {{K_n},{K_1}} \right)} \right) - 55} \right)}^2}} \right|} \right)} \end{array} $ | (50) |
可将式(48—50)的目标函数记为
| $ Ti\left( {{\xi _1},{\xi _2},\eta } \right) = {\rm{Time}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) $ |
| $ Th\left( {{\xi _1},{\xi _2},\eta } \right) = {\rm{Threat}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) $ |
| $ Fu\left( {{\xi _1},{\xi _2},\eta } \right) = {\rm{Fuel}}\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) $ |
决策者对无人机ISR任务中的各个目标函数的偏好不同,相应赋予不同的权重,由此可以建立不确定随机单目标规划模型
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{\pi \left( X \right) \in D} U\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right) = \\ \;\;\;\;\;\;{\lambda _1}Ti\left( {{\xi _1},{\xi _2},\eta } \right) + {\lambda _2}Th\left( {{\xi _1},{\xi _2},\eta } \right) + \\ \;\;\;\;\;\;{\lambda _3}Fu\left( {{\xi _1},{\xi _2},\eta } \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;Ch\left\{ {{\rm{Fu}}\left( {{\xi _1},{\xi _2},\eta } \right) - 9 \le 0} \right\} \ge 1 \end{array} \right. $ | (51) |
式中
目标函数之间存在复杂的耦合关系,难以同时最优化所有目标,得到最优的飞行路径,所以可以求解Pareto有效飞行路径。由于无人机ISR任务分配问题是典型的不确定随机多目标规划问题,本节将结合在上节中提出的I-URMOP求解方法在PEV准则下对问题进行求解。根据PEV准则,不确定随机单目标规划问题式(51)可以转化为等价确定性规划模型如式(52)所示,即有
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{\pi \left( X \right) \in D} \left\{ {E\left[ {U\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\left. {V\left[ {U\left( {\pi \left( X \right),{\xi _1},{\xi _2},\eta } \right)} \right]} \right\} = \\ \;\;\;\;\;\;\;{\lambda _1}\left( {E\left[ {Ti\left( {{\xi _1},{\xi _2}\eta } \right)} \right] + V\left[ {Ti\left( {{\xi _1},{\xi _2},\eta } \right)} \right]} \right) + \\ \;\;\;\;\;\;\;{\lambda _2}\left( {E\left[ {Th\left( {{\xi _1},{\xi _2}\eta } \right)} \right] + V\left[ {Th\left( {{\xi _1},{\xi _2},\eta } \right)} \right]} \right) + \\ \;\;\;\;\;\;\;{\lambda _3}\left( {E\left[ {Fu\left( {{\xi _1},{\xi _2}\eta } \right)} \right] + V\left[ {Fu\left( {{\xi _1},{\xi _2},\eta } \right)} \right]} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;\;Ch\left\{ {{\rm{Fu}}\left( {{\xi _1},{\xi _2},\eta } \right) - 9 \le 0} \right\} \ge 1 \end{array} \right. $ | (52) |
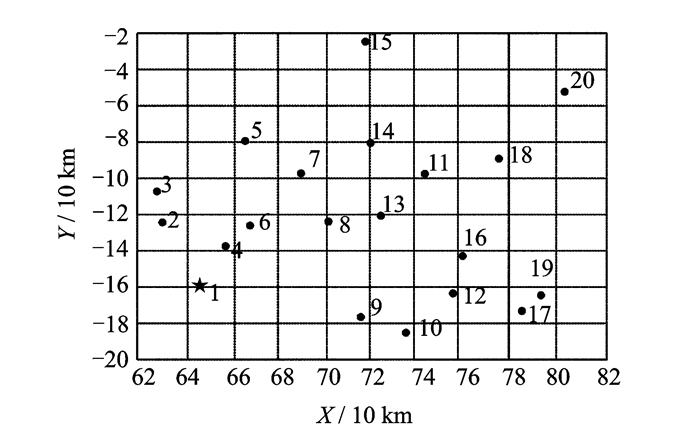
本节构建1个带有19个任务点的不确定随机多目标无人机ISR任务分配问题。无人机执行ISR任务区域如图 2所示,对无人机所有ISR任务点进行编号,无人机基地编号为1。所有任务点和无人机基地坐标如表 1所示。假定无人机ISR任务分配问题中的3个变量分别服从线性不确定分布,之字形不确定分布和指数型概率分布,即ξ1~L(1.5, 12), ξ2~Z(0.8, 1.3, 1.8), η~ε(0.6)分别记为Φ1(x), Φ2(x), Ψ(x)。
|
图 2 无人机执行ISR任务区域示意图 Figure 2 Schematic diagram of unmanned aerial vehicle (UAV) executing ISR mission area |
| 表 1 所有ISR任务位置点的坐标 Table 1 Coordinates of all ISR task location points |
变量分布的取得以ξ1为例进行说明,邀请专家对敌人火力部署情况对无人机执行任务的影响进行估计可知,相关领域专家认为敌方火力部署情况对目标函数的影响程度小于12的信度为100%,认为敌方火力部署情况对目标函数的影响成都小于1.5的信度为0%,如果火力部署情况的影响在[1.5, 12]内和专家信度的关系为线性,由此得到ξ1的分布, 即有
| $ {\mathit{\Phi }_1}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} 0&{x \le 1.5}\\ {\frac{{\left( {x - 1.5} \right)}}{{\left( {12 - 1.5} \right)}}}&{1.5 < x \le 12}\\ 1&{x > 12} \end{array}} \right. $ | (53) |
同理可得ξ2~Z(0.8, 0.9, 1.8)。
η~ε(0.6)是通过对历史数据进行拟合,发现该变量基本符合指数分布的特征,根据矩估计求得相应的参数。
根据不确定理论计算法则可得,相关变量可计算为:Φ1-1(α)=1.5+10.5α,Φ2-1(α)=0.8+α,
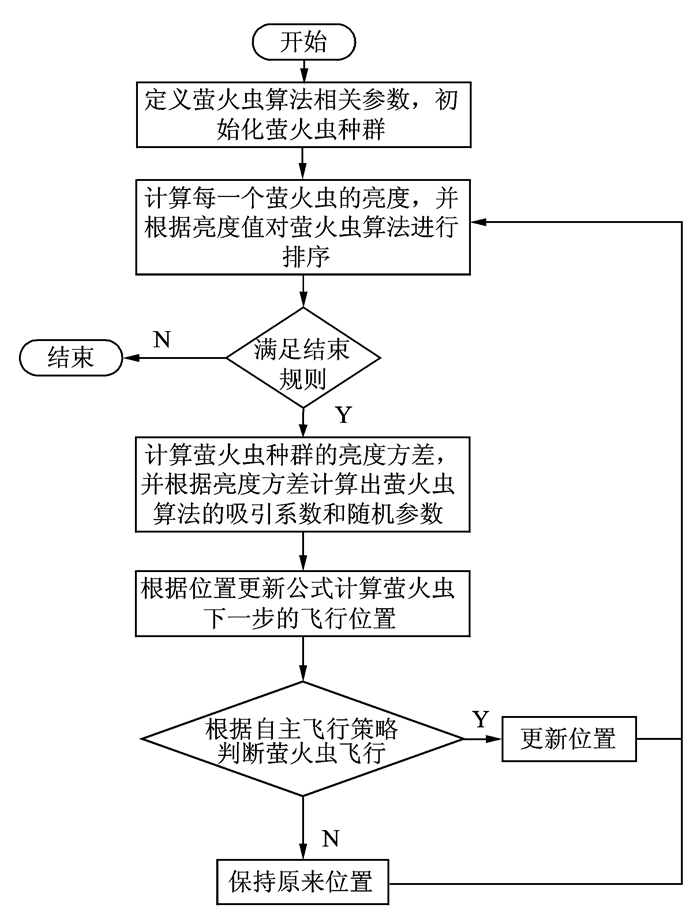
针对决策者对各个目标的不同认识与偏好,对该不确定随机规划模型赋予不同的权值。本节取λ1=0.6, λ2=0.2, λ3=0.2,考虑转化后的目标函数仍然非常复杂且局部极小点较多,因此采用改进的萤火虫算法(Firefly algorithom, FFA)进行求解,求解流程图如图 3所示。算法的初始参数设置为:β0=1.0, γe=1.0, γb=0.7, αe=0.2, αb=1.0, k=6。
|
图 3 改进的萤火虫算法流程图 Figure 3 Improved flow chart of firefly algorithm |
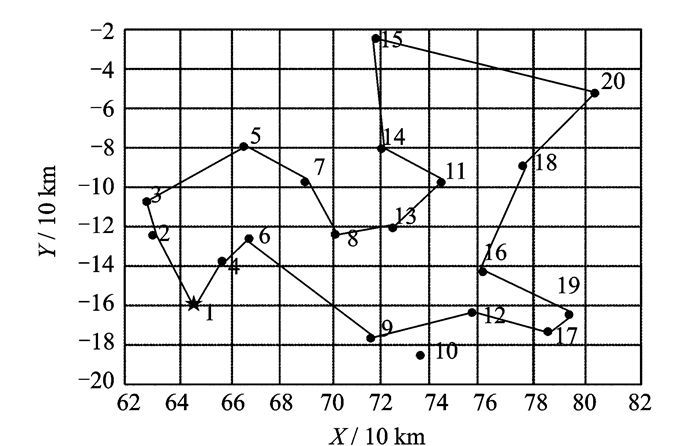
萤火虫算法的收敛速度如图 4所示。从图中可知,大约在第105代时,迭代收敛,系统趋于稳定。由此可得,无人机执行ISR任务飞行路径,示意图如图 5所示。PEV准则下的有效飞行序列:1→4→6→9→10→12→17→19→16→18→20→15→14→11→13→8→7→5→3→2目标函数值。Time=14.856 1 h, Threat=0.364 5, Fuel=7.956 1 t。

|
图 4 各代最短长度收敛曲线 Figure 4 The shortest length convergence curve of each generation |
|
图 5 无人机执行ISR任务飞行路径示意图 Figure 5 Schematic diagram of flight path for unmanned aerial vehicle to perform ISR mission |
实例结果表明,本文提出的模型及求解方法可以有效解决无人机任务分配问题,为建立复杂战场环境下的无人机作战任务规划系统提供决策支持。
4 结束语(1) 传统求解方法对不确定随机多目标规划问题求解忽略了原问题的不确定随机性,特别是当各个目标函数之间存在相同的不确定随机变量时,这样的方法忽略了各个不确定随机目标之间的相关性。针对该问题,本文引入不确定随机变量,建立了不确定随机多目标规划模型。
(2) 为求解I-URMOP问题,引入不确定随机变量间的序关系定义了I-URMOP问题的有效解,基于变量间的序关系将不确定随机多目标规划问题转化为不确定随机单目标规划问题。通过引入PEV准则将不确定随机单目标规划问题转化为确定的单目标规划问题,同时证明求解得到的最优解是原问题的有效解。
(3) 为求解无人机ISR任务分配问题,改进的FFA算法,最终得到了无人机的有效飞行序列,验证了模型的有效性及求解的正确性。
| [1] |
MISHRA S K.
Second order mixed symmetric duality in non-differentiable multi-objective mathematical programming[J]. Journal of Applied Analysis, 2007, 13(1): 117–132.
|
| [2] |
LI J, TANG L, SUN X, et al.
Oil-importing optimal decision considering country risk with extreme events:A multi-objective programming approach[J]. Computers and Operations Research, 2014, 42: 108–115.
DOI:10.1016/j.cor.2011.10.010
|
| [3] |
欧建军, 张安, 钟麟.
基于多目标优化决策的飞机维护计划研究[J]. 系统工程理论与实践, 2015, 35(5): 1346–1350.
OU Jianjun, ZHANG An, ZHONG Lin. Maintenance scheduling of aircrafts based on multi-criteria optimization and preference programming[J]. Systems Engineering-Theory & Practice, 2015, 35(5): 1346–1350. |
| [4] |
陈春良, 陈伟龙, 陈康柱, 等.
考虑非遍历的抢修任务多目标动态调度[J]. 兵工学报, 2017, 38(8): 1593–1602.
DOI:10.3969/j.issn.1000-1093.2017.08.018 CHEN Chunliang, CHEN Weilong, CHEN Kangzhu, et al. Multi-objective and dynamic scheduling of battlefield rush-repair tasks based on non-ergodicity[J]. ACTA ARMAMENTAR Ⅱ, 2017, 38(8): 1593–1602. DOI:10.3969/j.issn.1000-1093.2017.08.018 |
| [5] |
LIU B.
Uncertainty theory:A branch of mathematics for modeling human uncertainty[M]. Berlin Heidelberg: Springer, 2010.
|
| [6] |
LIU B.
Uncertainty distribution and independence of uncertain processes[J]. Fuzzy Optimization & Decision Making, 2014, 13(3): 259–271.
|
| [7] |
LIU B, CHEN X.
Uncertain multiobjective programming and uncertain goal programming[J]. Journal of Uncertainty Analysis & Applications, 2015, 3(1): 1–8.
|
| [8] |
LIU Y.
Uncertain random programming with applications[J]. Fuzzy Optimization & Decision Making, 2013, 12(2): 153–169.
|
| [9] |
祁晓明, 魏瑞轩, 周凯.
面向多威胁的无人机智能目标跟随策略设计[J]. 北京航空航天大学学报, 2016, 42(4): 780–788.
QI Xiaoming, WEI Ruixuan, ZHOU Kai. Intelligent target following strategy design for UAV against multi-threats[J]. Journal of Beijing University Aeronautics and Astronautics, 2016, 42(4): 780–788. |
| [10] |
LIU Zhong, GAO Xiaoguang, FU Xiaowei.
Coalition formation for multiple UAVs cooperative search and attack with communication constraints in Unknown Environment[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2017, 34(6): 688–699.
|
| [11] |
周瑞, 黄长强, 魏政磊, 等.
MP-GWO算法在多UCAV协同航迹规划中的应用[J]. 空军工程大学学报(自然科学版), 2017, 18(5): 24–29.
DOI:10.3969/j.issn.1009-3516.2017.05.005 ZHOU Rui, HUANG Changqiang, WEI Zhenglei, et al. Application of MP-GWO algorithm in multiple cooperating ucav path planning[J]. Journal of Air Force Engineering University(Natural Science Edition), 2017, 18(5): 24–29. DOI:10.3969/j.issn.1009-3516.2017.05.005 |
| [12] |
KIM H, JEON B I, LEE N, et al.
Development of mission analysis and design tool for ISR UAV mission planning[J]. Journal of the Korean Society for Aeronautical & Space Sciences, 2014, 42(2): 181–190.
|
| [13] |
WANG Z, ZHENG M, GUO J, et al.
Uncertain UAV ISR mission planning problem with multiple correlated objectives[J]. Journal of Intelligent & Fuzzy Systems, 2017, 32(1): 321–335.
|
| [14] |
WANG Z, GUO J, ZHENG M, et al.
Uncertain multiobjective traveling salesman problem[J]. European Journal of Operational Research, 2015, 241(2): 478–489.
DOI:10.1016/j.ejor.2014.09.012
|
| [15] |
LIU B, LIU Y K, LIU Y.
Expected value of fuzzy variable and fuzzy expected value models[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(4): 445–450.
DOI:10.1109/TFUZZ.2002.800692
|
| [16] |
LIU Y, LIU B.
Expected value operator of random fuzzy variable and random fuzzy expected value models[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2003, 11(2): 195–215.
DOI:10.1142/S0218488503002016
|
| [17] |
LIU Y, HA M.
Expected value of function of uncertain variables[J]. Journal of Uncertain Systems, 2010, 3(4): 181–186.
|
| [18] |
LIU Y.
Uncertain random variables:A mixture of uncertainty and randomness[J]. Soft Computing, 2013, 17(4): 625–634.
DOI:10.1007/s00500-012-0935-0
|
 2018, Vol. 50
2018, Vol. 50


