2. 大连理工大学土木工程学院, 大连, 116024
2. School of Civil Engineering, Dalian University of Technology, Dalian, 116024, China
在工业生产和日常生活中存在着大量的振动现象,这些振动往往会对生产、生活造成不良影响,例如:在机械加工领域,振动会引起机械结构的磨损,降低加工、安装精度;在交通运输领域,振动会降低交通工具的安全度和舒适度;在航天领域,振动会引发飞行器故障而致其失效;在土木工程领域,振动会导致桥梁断裂、楼房倒塌、甚至造成人员伤亡等。总体而言,这些危害可总结为3类:结构安全性危害、仪器装备功能性危害和人员舒适性危害[1-2]。为了消除或降低振动带来的诸多消极影响,振动控制技术及其在工程领域中的应用便显得极为重要。
目前来讲,用于工业振动控制的方法有隔振、吸振、阻振、消振及结构修改等,在选择时需要对振源特性及振动抑制目标进行综合考虑[3-4]。根据是否需要外界能源驱动,振动控制又分为被动控制与主动控制。其中,因被动控制具有不需要外界能源、结构简单、易于实现、经济性与可靠性好等优点,其在工程实际中得到了广泛应用。但随着生产、生活环境的改善,被动控制因自身的局限性,越来越难以满足人们对振动环境和产品与结构振动特性的要求;主动控制技术由于具有效果好、适应性强等特点,得到了学者们的广泛关注,并且作为一条重要的振动控制新途径,被应用到结构振动控制中来[5]。
常见的振动主动控制系统,一般由受控对象、作动器(有时含惯性质量)、控制器、传感系统及能源几个部分组成[6]。当主动控制系统运行时,由配置在被控对象上的传感系统测量其振动,传感器的输出信号经适调电路放大处理后传送到控制器,控制器按预先设定的控制算法计算控制律,作动器在控制器指令控制下输出主动控制力并作用于被控对象,从而实现被控系统的振动控制。
1 旋转激励作动器旋转激励作动器是主动控制系统中作动器的一种,不同于传统的液压作动器、直线电机作动器等,该类型的作动器通过旋转形式输出转矩、转速或转角等控制量,以旋转电动机最为常见。
传统的直线作动器以惯性质量为支撑点,通过驱动惯性质量加速、减速,向被控对象施加主动控制力(图 1(a))。目前的直线作动器主要包括液压作动器和伺服电机作动器(需传动装置),这两种作动器均存在一些难以克服的缺点,限制了主动控制系统的应用。液压作动系统构造复杂、制造成本高、需要定期换油、维护成本高且系统运行噪声大,电液能量转换后能源利用效率降低。伺服电机需要借助机械传动部件(滚珠丝杠等)等中间环节将电机旋转运动转换为惯性质量的直线运动,并传递主动控制力,仍属于接触式传力,存在响应慢的问题;且惯性质量运动时与滑轨接触,接触面间的摩擦会消耗较多的能量。此外,控制系统中被控对象和惯性质量的直接连接还会产生行程受限问题[7-8]。

|
图 1 直线作动器与旋转激励作动器 Figure 1 Linear actuator and rotating a ctutor |
在采用基于旋转激励作动器的主动控制系统中,作为控制力输出支撑点的惯性质量在作动器的驱动下做旋转运动(图 1(b)),从而避免了作动器行程受限、直线度难以保证等问题。旋转激励作动器可采用直驱方式驱动惯性质量,可避免引入机械传动部件而造成的响应慢、引入不期望的摩擦等问题,从而可实现更高的控制效率。相较于液压作动器,电动机具有占用空间小、易集成、控制简便以及方便维护等优点。这些都赋予了旋转激励作动器,尤其是基于电动机的旋转激励作动器更大的应用价值。需注意的是,旋转激励作动器所驱动的不一定是偏心质量,在惯性质量非偏心的情况下,作动器可向被控对象施加转矩,抑制被控对象在旋转自由度上的振动(如旋转激励作动器用于卫星姿态稳定控制的情形)。
为了更加清晰地理解旋转激励作动器的概念,本文结合具体工程实例对旋转激励作动器进行分析说明。本文主要对这类旋转激励作动器在航天、交通运输和防灾减灾等不同领域内振动控制问题中的应用及相关的实验研究进行分析总结。
2 在飞行器振动控制中的应用旋转激励作动器在飞行器中的应用为双自旋卫星的姿态稳定控制,利用陀螺的定轴性原理,通过转子旋转实现卫星平台的姿态稳定,使卫星有效载荷稳定地对地定向;考虑到实际卫星不是刚体,存在许多弹性部件,因此卫星的姿态稳定过程中必然会包含振动控制的内容,即系统残余振动的消除。
2.1 双自旋卫星姿态稳定双自旋飞行器一般由平台和转子组成,两者用轴承联接起来,如图 2(a)所示。在刚进入轨道时,平台和转子以相同速度绕转轴旋转,两者间不存在角速度差。为了消除平台的转动,需要通过安装在平台和转子间的电机输出控制转矩,使得转子绕转轴转速增加,同时使平台转速减小,当自旋体转速为零时,电机停止工作,从而实现卫星的消旋,消除其旋转方向的残余振动,这时平台上的有效载荷(如探测仪器、通信天线等)将稳定地对地定向。在这个过程中,平台和转子间的电动机即为旋转激励作动器,转子作为惯性质量不存在偏心,旋转激励作动器将其作为支撑点向平台施加转矩,从而实现平台的镇定。中国的“东方红2号”通信卫星和“风云2号”气象卫星等都采用了双自旋稳定的控制方式,如图 2(b)所示。

|
图 2 双自旋卫星示意图及其工程实例:风云二号气象卫星 Figure 2 Sketch of dual-spin spacecraft and its engineering example: Fengyun II meteorological sat ellite |
在实际卫星姿态稳定过程中,因驱动轴与卫星惯性主轴不完全重合等原因,可能会造成电机输出的能量注入到系统的其他动态中,使系统出现不期望的动态,导致消旋失败,其中一种情形称为进动相位锁定(Precession phase lock, PPL),该现象的出现在于转子的旋转运动与卫星角动量进动发生共振[9],正是通过对该现象的研究,学者们得出了一种研究机械振动抑制的重要基准模型——基于旋转激励作动器的平移振荡器。
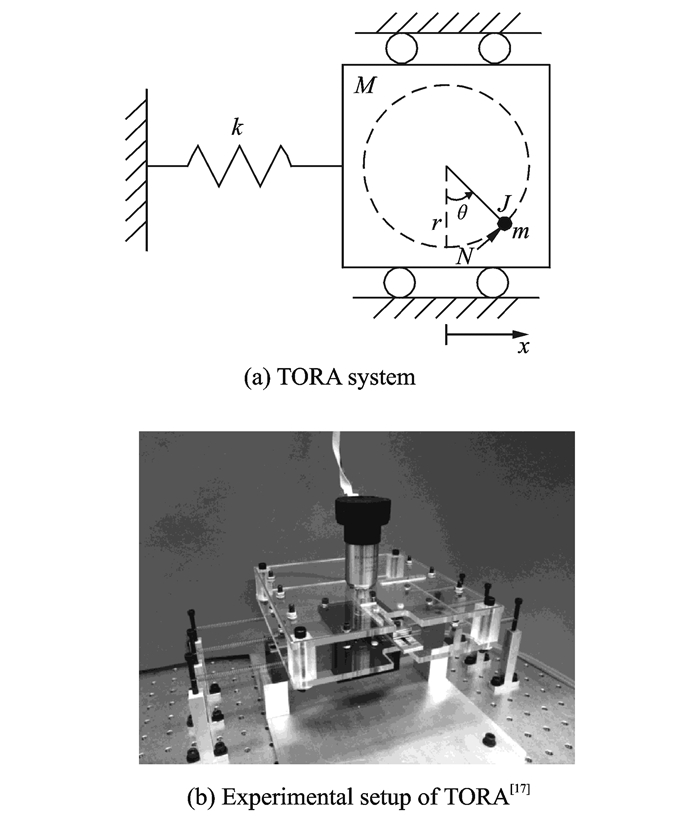
2.2 基于旋转激励作动器的平移振荡器为了研究双自旋飞行器的进动相位锁定现象,Yee [10]提出了一种与双自旋卫星数学模型类似,但结构更简单的基准模型——基于旋转激励作动器的平移振荡器(Translational oscillator with rotating actuator,TOR A)。该系统由一个未驱动的平移振荡器和受转矩驱动的旋转偏心惯性质量组成,如图 3(a)所示。其中小车(平移振荡器)与弹簧相连,在水平面内作一维往复直线运动。小球(惯性质量)在电机(或其他出力装置)输出转矩的作用下在平面内转动。因为小车平移运动与小球旋转运动之间的耦合关系,小球在转矩驱动下发生的旋转运动会对小车的直线运动造成影响。
|
图 3 TORA系统及其实物实验平台 Figure 3 TORA system and its experimental setup |
TORA系统的控制目标通常为小车位移及小球转角的镇定,考虑到TORA系统只有1个控制输入,即输入转矩,但其控制目标为两个独立状态变量的镇定问题,因此TORA系统是1个典型的欠驱动系统[11]。TORA系统中包含了单自由度弹簧-质量系统,小车的镇定也是1个典型的振动控制问题,故该系统常被作为研究机械振动控制的一个重要基准模型。在TORA系统被提出后,学者们对其振动控制问题进行了大量的理论[12-16]以及实验研究[17],图 3(b)为Bupp等搭建的TORA实验平台,用来对TORA系统的各种非线性控制算法控制效果进行分析和比较。
将TORA系统称为基于旋转激励作动器的平移振荡器,由此可以得到旋转激励作动器的直观认识,像双自旋飞行器中驱动转子转动,TORA系统中驱动偏心质量的转矩输出装置,其通过旋转形式输出转矩、转速或转角等控制量,即所谓的旋转激励作动器。
3 在船体振动控制中的应用旋转激励作动器在船体振动控制中的应用为基于兰切斯特原理的电动消振器,其通过旋转激励作动器输出控制力实现船舶主机和螺旋桨引起的船体结构振动抑制,该基于旋转激励作动器的船用电动消振器已经实现了商品化。
3.1 船体振动船舶大多采用柴油机作为动力装置,由其运转时激发的振动,特别是过度的振动易产生严重后果,会对船体结构的安全性和船舶机械的可靠运行造成不良影响,严重时甚至会造成船舶结构的破坏;除此之外,船舶振动对于搭乘人员的舒适性、船员的工作效率所造成的影响也不容忽视。
现代船舶柴油机动力装置向着轻型、强载和高速化趋势不断发展,这使得对其激发的振动控制提出了更高的要求[18]。如图 4所示,船舶振动的内部振源主要是船舶主机和螺旋桨,因为两者同轴,其激发的振动响应常常以某一基频分量为主,并且与主机轴的转速相关,当结构的固有频率与主机轴旋转频率相等时,会引发共振。不同于其他领域的结构振动,船舶工程领域中所要消减的振动属于低频范围(通常在50 Hz以下,主要集中于2~20 Hz范围内),但振动功率较大(几百瓦至几十千瓦)。基于兰切斯特原理的电动消振器具有输出控制力频率低、输出功率大的特点,能够适应以上所述船舶结构振动的特点。

|
图 4 船体振动两种振源:主机和螺旋桨 Figure 4 Vibration sources of ship: Marine engine and propeller |
3.2 基于兰切斯特原理的电动消振器
基于兰切斯特原理的电动式船用机械作动器是一种能够感受和跟踪振动响应或干扰力,对速度和相位信号进行分析处理,产生相应的控制力,以抵消结构振动响应的一种电气机械装置。
主动消振器由传感器、同步装置和执行机构组成。传感器检测消振器与工作机械主轴速度、相位以及振动响应,作为同步装置的输入信号,同步装置对输入信号作相应处理,控制驱动电机加速或减速,执行机构便可产生具有最优幅值和相位的控制力[19-20]。该消振器在运行时,作为旋转激励作动器的电动机驱动两个具有相同质量的偏心块以k倍发动机主轴转速同步反向旋转,两旋转偏心块的离心力在水平(竖直)方向上互相抵消,而在竖直(水平)方向上叠加(图 5),这样就在竖直或水平方向上产生了幅值和相位可调且简谐变化的控制力,如控制力引起的结构振动与柴油机k阶激扰引起的振动大小相等,方向相反,即可实现主动消振[21]。

|
图 5 船用电动消振器 Figure 5 Rot ating actuator for mitigation of ship vibration |
传统的电动消振器产生的消振力一般只能用停机增减偏心块质量的办法实现幅值调节,但并不能做到无级调整。为解决这一限制,釜山大学的学者研制了一种能实时跟踪振动响应相位与幅值的主动式消振装置[22],其通过调节旋转惯性质量的偏心距来调节力幅,具体如图 6所示。

|
图 6 釜山大学主动消振装置 Figure 6 Active vibration damping device in P usan National University |
消振力调节机构由连杆、偏心质量、移动部分和导轨组成。左端连杆轴向固定,右端连杆与移动部分铰接。移动部分位置由交流伺服电机控制,它通过位置控制驱动带驱动丝杠使移动部分沿导轨做轴向移动,消振力幅值的改变量与偏心距的改变量成正比,交流感应电机被用于相位控制。
3.3 工程应用1974年日本石川重工研制出一种独立的电动消振机,拖动电动机由船舶电网直接供电,并通过可控硅控制定子三相绕组高转差率三相异步电动机。该电动消振器被应用在一艘26 000 t集装箱船上,通过实船测试发现:该系统与由柴油机主轴驱动的消振机相比,总质量减轻40%,安装面积减少65%,其实船消振效果明显,达到70%。特别是因为它不再与主机联在一起,可成为一种独立的船舶机械,为以后的各种型号消振机设计所效法。西芝电机在1975年研制出了一种自动追从式电动消振器,该消振器被应用在了“亚洲鹰号”集装箱船上[23]。丹麦Gert sen&Olufsen公司生产的振动补偿器已形成系列产品(图 7)。该公司已经市场化的产品包括垂直型(如C-40H)和水平型(如C-200V1)两个系列,最大消振力从6×104 N至7×105 N[24]。

|
图 7 Gertsen & Olufsen公司生产的振动补偿器 Figure 7 Vibration compensator(Gertsen & Ol ufsen) |
4 在桥梁风致振动控制中的应用
旋转激励作动器在桥梁减振防灾中的应用为双转子阻尼器(Twin rotor damper, TRD),相较于传统的主动质量阻尼器,双转子阻尼器具有能耗低、容易控制等优点,适用于抑制风载荷引起的桥体周期性振动。
4.1 桥体风致颤振为了满足日益增长的交通运输需求,现代桥梁的跨径越来越大:悬索桥方面,美国金门大桥的跨径达到了1 280 m;1998年英国建成的明石海峡大桥使悬索桥最大主跨跨径记录达到了1 991 m;2009年建成的俄罗斯岛大桥则保持着斜拉桥的最大跨径记录,为1 104 m。中国的大跨度桥梁建造技术也取得了巨大进展,刚刚建成、尚未正式通车的港珠澳大桥不但是世界上最长的跨海大桥(全长55 km),其主体部分桥跨也达到了1 150 m。
随着桥梁跨度的不断增大,结构刚度和阻尼进一步降低,使得桥梁对风载荷更加敏感,风致振动成为大跨度桥梁建设中的瓶颈。风载荷能够激发出桥梁不同形式的振动,包括:颤振、驰振、抖振与祸激振动等。其中颤振属于发散性的自激振动,是破坏性最为严重的风致振动形式[25]。塔科马悬索桥的风致颤振损毁便是一个典型的例子,如图 8所示。为了避免桥梁颤振造成的极端破坏,学者们对桥梁颤振的控制进行了广泛的研究。

|
图 8 塔科马悬索桥风致垮塌 Figure 8 Collapse of Tacoma narrows bridge caused by wind-induced vibration |
4.2 双转子阻尼器
能够应用到桥梁风致颤振控制中的主动质量阻尼器(Active mass damper, AMD)应该满足如下的要求:使用功率较小的出力装置产生足够大的主动控制力;使用较小的惯性质量产生足够的控制效果。但是传统的AMD系统存在能耗高、占用空间大等问题,无法满足实际工程要求。为此,德国学者Starossek等提出了一种新型的AMD装置——双转子阻尼器TRD,将其应用到了桥体的风致颤振控制中[26]。
TRD装置由两个偏心转子构成,每个转子均由旋转激励作动器驱动,如图 9所示。每个转子包括偏心质量以及连接偏心质量和作动器的轻杆,两个偏心质量相同均为mc,两轻杆长度均为rc,两转子在平行平面内相向转动,转速相同为ω。通过对两个转子的转速及初始相位进行调节,选取合适的参数,可以产生不同幅值和方向的主动控制力时程,实现不同的控制目标。

|
图 9 TRD装置原理图 Figure 9 Schematic of TRD |
文献[27]给出了将TRD应用到桥梁的风致颤振控制中的具体方案,因为风载荷会引起桥体的垂向振动和绕箱梁中心转动振动,采用两组TRD对桥体振动进行控制,如图 10所示。两组TRD的配置形式可同时在桥体两个自由度上产生相应的控制力及转矩,从而实现桥体在垂向和旋转两个自由度上的风激振动抑制。采用TRD抑制桥体风致颤振响应的基本思路:通过调节转子转动的相位,使偏心质量离心力方向始终与桥体振动速度方向相反,即两者相位相差180°,这样可保证TRD产生的离心力始终对结构作负功,起到附加阻尼的作用,从而将结构振动的动能消耗掉,实现振动抑制。需要指出,因为TRD在工作时以匀速旋转运动为主,通过施加离心力减小结构响应,故其适用于风载荷引起的结构周期性响应抑制,而对非周期性结构响应抑制效果则不是很理想。

|
图 10 桥梁节段中TRD配置示意图 Figure 10 Configuration of TRDs in bridge section |
Bäumer和Scheller等[28-31]通过风洞实验,验证了TRD对桥体风致颤振的抑制效果,TRD的引入可以使得桥梁节段的颤振临界风速得到明显提高(风洞实验结果显示,通过引入TRD控制颤振临界风速可由38.5 m/s2提高到43.9 m/s2)。在保证控制效果的同时,TRD装置还具有低能耗的优点,这是因为TRD装置运行时,主要是偏心质量旋转产生的离心力起作用,该离心力在匀速状态下产生,不需要对惯性质量进行加速或减速。
文献[32, 33]研究了基于T RD的切换控制策略,通过使TRD在不同的控制模式之间进行切换,完成不同外部载荷激发的不同类型振动的抑制。Bäumer等[29]通过实验分析了TRD对桥体步行激励振动抑制的效果(图 11),这些研究对于提高TRD装置的工程应用价值具有重要意义。

|
图 11 基于TRD的桥体振动抑制实验平台 Figure 11 Experimental setup of bridge vibra tion suppression based on TRD |
5 在建筑物地震激励响应控制中的应用
旋转激励作动器在建筑物防灾减震中的应用为基于旋转激励作动器的主动质量阻尼器。作动器旋转运动的引入使该新型的主动质量阻尼器成为了一种特殊的非线性AMD,虽然为其控制系统设计造成了困难,但同时也使得新型主动控制系统具有了容易集成,避免行程受限的优点;且惯性质量直接由作动器驱动,避免了传动部件引起的附加摩擦及响应慢等问题。
5.1 基于旋转激励作动器的AMD装置因为地震能量比较集中,当其作用在建筑物上时,可能会造成建筑物某些部位的地震反应过大,致使主体承重结构严重破坏、甚至倒塌,或者虽然主体结构未破坏,但装饰、装修等非结构构件损坏而导致结构无法继续使用。这些由地震激发的建筑物剧烈振动会造成巨大的经济损失甚至是人员伤亡。因为具有控制效果好、响应快等优点,主动质量阻尼技术是结构地震响应抑制中应用最多的一种控制手段[34]。大量理论分析和实际数据都表明,在建筑物中恰当部位配置AMD装置能够有效地减小结构动力反应,降低结构构件的破坏或损伤几率,实现经济性、安全性与可靠性的合理平衡。
现有的主动质量阻尼装置多以液压系统或伺服电机作为驱动装置,液压系统存在构成复杂、能耗高且占用空间大等问题,伺服电机存在需传力部件、响应慢且行程受限等缺点,使AMD的工程应用受到了限制。针对这些问题,文献[35]提出了一种基于旋转激励作动器的新型AM D装置(Active mass damper with rotating actuator,R-AMD),其采用旋转激励作动器驱动,具有系统构成简单、占用空间小和能耗低等优点。
R-AMD装置如图 12所示,其具有与TRD相似的配置形式,但是其工作模式和控制方案与TRD完全不同。由于地震载荷能量比较集中,作用在结构上时往往会激发出结构的多阶模态,此时TRD所采用的匀速旋转控制模式不再适用,为此为R -AMD设计了摆动控制模式,在该控制模式下,惯性质量在一定范围内作快速摆动,出力变化(方向、大小)较快、功率大,可在较短时间内吸收地震施加到结构上的能量。

|
图 12 R-AMD与配置R-AMD的单自由度结构 Figure 12 R-AMD and SDOF structure installed with R-AMD |
5.2 振动台试验
为验证R-AMD控制系统的控制效果,搭建了如图 13所示的R-AMD控制系统实物平台,并在该平台上进行实验。控制系统将dSPACE作为控制器,主要应用了dSPACE系统的“快速控制原型”功能。需要dSPACE系统的1个AD接口采集位移传感器输入的电压信号,1个差分正交信号接收接口接收编码器输出的角度信息,以及1个DA端口用于输出dSPACE计算出的控制信号给电机驱动器,以实现电机控制。电机与编码器同轴,这样编码器就可以测出惯性质量在电机带动下所转过的角度。

|
图 13 R-AMD控制系统试验平台 Figure 13 Experimental setup of R-AMD control system |
在试验过程中可采用不同的控制算法对R-AMD系统进行控制,例如反歩法[36]、反馈线性化方法[16]、滑模算法[37-38]以及最优控制算法[39-40]等。图 14给出采用基于θ-D方法的非线性最优控制算法控制R-AMD系统时得到的实验结果,可以发现通过R-AMD系统向单自由度结构施加控制力能够有效减小结构地震响应:对于El Centro地震波,位移最大值可降低14.5%,均方根值降低33.3%;对于Kobe地震波,最大值降低了37.5%,均方根值降低了44%。

|
图 14 不同地震载荷(El Centro, Kobe)作用下的结构位移响应 Figure 14 Structural displacement responses under EI Centro and Kobe excitation |
不同于TRD控制桥梁风致振动时产生的是离心力,R-AMD抑制结构地震响应时,同时产生离心力与切向力,为了研究两种不同的分力对于结构振动抑制所起的作用,计算出了两种力成分对于结构所做的功,结果如图 15所示。可以发现在不同的地震载荷下,两种力均对结构作负功,但是作功大小却相差很大,切向力对结构所作负功远远多于离心力所做的功,说明R-AMD产生的控制力中切向力对结构的地震响应抑制其主要作用。而这也证明了R-AMD与TRD的区别所在,两者对于结构振动抑制,具有完全不同的控制方案及工作方式,TRD通过施加离心力减小结构响应,而R-AMD主要通过施加切向力完成结构响应抑制,这也决定了两者适用于不同的载荷,TRD适用于风载荷引起的结构周期性响应抑制,而R-AMD则更适合于地震载荷引起的建筑物响应抑制。

|
图 15 不同地震载荷(El Centro, Kobe)作用下,施加R-AMD主动控制时各力成分做功 Figure 15 Work done by different components of R-AMD control force under El Centro and Kobe excitations |
6 结束语
通过对旋转激励作动器进行的分析,及对其在各个领域中的应用进行的总结可以发现,相较于传统的直线型作动器,旋转激励作动器具有易集成、能耗低、占用空间小且易于电控等明显优点,而这也使其具有了广阔的应用前景。除了文中提到的应用领域之外,其在车辆主动悬架控制、防抖云台和柔性机械臂防抖等领域也具有较大的潜在应用价值。这是因为,不管是车辆悬架、防抖云台还是工业机械臂,都对振动抑制装置的大小、能耗和易集成度具有很大要求,而旋转激励作动器在这些方面具有明显优势;此外,由旋转运动产生的控制力具有较低的伺服刚度,对于保证控制系统柔顺性,避免激发被控系统的不期望动态具有重要意义。
需要提出的是,基于电动机的旋转激励作动器在功率密度、出力幅值方面的表现要差于液压作动器,这给采用旋转激励作动器控制规模较大系统(如土木结构)的振动带来了挑战。为了解决旋转激励作动器这方面的不足,并充分发挥电力传动系统易于集成、占用空间小的优点,可采用分布式多机协作的方式提高作动器的功率密度。与此同时,具有非线性特性的旋转激励作动器的分布控制问题也会对控制理论的研究提出新的要求,而这也是本领域一个具有挑战性的研究方向。
| [1] |
徐建.
建筑振动工程手册[M]. 北京: 中国建筑工业出版社, 2002.
XU Jian. Building vibration engineering manual[M]. Beijing: China Building Industry Press, 2002. |
| [2] |
徐建.
隔振设计规范理解与应用[M]. 北京: 中国建筑工业出版社, 2009.
XU Jian. Understanding and application of vibration isolation design specifications[M]. Beijing: China Building Industry Press, 2009. |
| [3] |
顾仲权, 朱德懋.
振动控制评述[J]. 噪声与振动控制, 1988(1): 5–13.
GU Zhongquan, ZHU Demao. Review of vibration control[J]. Noise and Vibration Control, 1988(1): 5–13. |
| [4] |
顾仲权, 马扣根, 陈卫东.
振动主动控制[M]. 北京: 国防工业出版社, 1997.
GU Zhongquan, MA Kougen, CHEN Weidong. Active vibration control[M]. Beijing: National Defend Industry Press, 1997. |
| [5] |
欧进萍.
结构振动控制——主动, 半主动与智能控制[M]. 北京: 科学出版社, 2003.
OU Jinping. Structural vibration control-active, semiactive and intelligent control[M]. Beijing: Science Press, 2003. |
| [6] |
YAMAMOTO M, AIZAWA S, HIGASHINO M, et al.
Practical applications of active mass dampers with hydraulic actuator[J]. Earth quake Engineering & Structural Dynamics, 2010, 30(11): 1697–1717.
|
| [7] |
张春巍.结构振动的电磁驱动AMD控制系统及其相关理论与试验研究[D].哈尔滨: 哈尔滨工业大学, 2005.
ZHANG Chunwei. Electromagnetic AMD systems and their relevant theory and experiments for structural vibration control[D]. Harbin: Harbin Institute of Technology, 2005. |
| [8] |
VENANZI I, IERIMONTI L, UBERTINI F.
An enhanced nonlinear damping approach accounting for system constraints in active mass dampers[J]. Journal of Sound & Vibration, 2015, 357: 2–15.
|
| [9] |
RAND R H, KINSEY R J, MINGORI D L.
Dynamics of spinup through resonance[J]. Internation al Journal of Nonlinear Mechanics, 1992, 27(3): 489–502.
DOI:10.1016/0020-7462(92)90015-Y
|
| [10] |
YEE R K. Spinup dynamics of a rotating system with limited torque[D]. LA: UCLA, 1981. |
| [11] |
高丙团, 陈宏钧, 张晓华.
一类欠驱动机械系统的非线性控制[J]. 控制与决策, 2006, 21(1): 104–106, 110.
DOI:10.3321/j.issn:1001-0920.2006.01.024 GAO Bingtuan, CHEN Hongjun, ZHANG Xiaohua. Nonlinear control for a class of underactuated mechanical systems[J]. Control and Decision, 2006, 21(1): 104–106, 110. DOI:10.3321/j.issn:1001-0920.2006.01.024 |
| [12] |
SPONG M W. Partial feedback linearization of underactuated mechanical systems[J]. Proc IEEE International Conference on Intelligent Robots and Systems.[S.l.]: IEEE, 1994, 1: 314-321. |
| [13] |
WAN C J, BERNSTEIN D S, COPPOLA V T.
Global stabilization of the oscillating eccentric rotor[J]. Nonlinear Dynamics, 1996, 10(1): 49–62.
DOI:10.1007/BF00114798
|
| [14] |
高丙团, 孙国兵.
TORA转子位置反馈的稳定控制方法[J]. 电机与控制学报, 2010, 14(8): 58–62.
DOI:10.3969/j.issn.1007-449X.2010.08.010 GAO Bingtuan, SUN Guobing. Stabilization control method with rotor angle feedback for TORA system[J]. Electric Machines and Control, 2010, 14(8): 58–62. DOI:10.3969/j.issn.1007-449X.2010.08.010 |
| [15] |
ALLEYNE A.
Physical insights on passivity-based TORA control designs[J]. IEEE Transactions on Control Systems Technology, 1998, 6(3): 436–439.
DOI:10.1109/87.668045
|
| [16] |
张宇, 郭源博, 李芦钰, 等.
基于最大反馈线性化的TORA系统非奇异镇定控制[J]. 控制与决策, 2018, 33(8): 1415–1421.
ZHANG Yu, GUO Yuanbo, LI Luyu, et al. Nonsingular controller for TORA system based on maximal feedback linearization[J]. Control and Decision, 2018, 33(8): 1415–1421. |
| [17] |
BUPP R T, BERNSTEIN D S, COPPOLA V T.
Experimental implementation of integrator backstepping and passive nonlinear controllers on the RTAC testbed[J]. Journal of Robust and Nonlinear Control, 1998(8): 435–457.
|
| [18] |
张阿舟.
实用振动工程[M]. 北京: 航空工业出版社, 1997.
ZHANG Azhou. Applied vibration engineering[M]. Beijing: Aeronautical Engineering Press, 1997. |
| [19] |
王滨庆.基于机械作动器的振动主动控制技术研究[D].哈尔滨: 哈尔滨工程大学, 2005.
WANG Binqing. The study of active vibration control technique based on mechanical actuator[D]. Harbin: Harbin Engineering University, 2005. |
| [20] |
韩广才.机械作动器在船舶减振上的应用研究[D].哈尔滨: 哈尔滨工程大学, 2005.
HAN Guangcai. The applied study of mechanical actuator on vbration control of ship[D]. Harbin: Harbin Engineering University, 2005. |
| [21] |
马葆庆.
国外的船舶电动消振装置[J]. 船海工程, 1989(2): 16–20.
MA Baoqing. Review of electric vibration-elimina ting device overseas[J]. Navy Engineering, 1989(2): 16–20. |
| [22] |
CHO D S, LEE S M.
Ship vibration control using a force adjustable mechanieal actuator[J]. Journal of Vibration Control, 1999, 5: 779–794.
DOI:10.1177/107754639900500507
|
| [23] |
曹云江.
NEBW1-8000EC型自动同步振动平衡器简介[J]. 天津航海, 2003(2): 14–17.
DOI:10.3969/j.issn.1005-9660.2003.02.007 CAO Yunjiang. Introduction to NEBW1-8000EC synchronous vibration balancer[J]. Tianjin Navy, 2003(2): 14–17. DOI:10.3969/j.issn.1005-9660.2003.02.007 |
| [24] |
GERTSEN & OLUFSEN A S. Introduction to the vibration compensator[EB/OL]. (2018-06-01). http://www.gertsen-olufsen.dk. |
| [25] |
KAZAMA K, YAMADA H, MIYATA T.
Wind resistant design for long span suspension bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54: 65–74.
|
| [26] |
STAROSSEK U, SCHELLER J. A novel active mass damper for vibration control of bridges[C]//Proceedings of the Fourth International IABMAS Conference. Boca Raton: CRC Press, 2008: 99-106. |
| [27] |
SCHELLER J, STAROSSEK U. A versatile active mass damper for structural vibration control[C]//Proceedings of the 8th International Conference on Structural Dynamics. Amsterdam: Elsevier, 2011: 1777-1784. |
| [28] |
BÄUMER R, STAROSSEK U.
Active vibration control using centrifugal forces created by eccentrically rotating masses[J]. Journal of Vibration & Acoustics, 2016, 138(4): 14.
|
| [29] |
BÄUMER R, TERRILL R, WOLLNACK S, et al.
Twin rotor damper for the damping of stochastically forced vibrations using a power-efficient control algorithm[J]. Journal of Sound & Vibration, 2018, 413: 308–331.
|
| [30] |
BÄUMER R, STAROSSEK U.
Closed-form steady-state response solution of the twin rotor damper and experimental validation[J]. Journal of Vibration and Acoustics, 2017, 139(2): 11.
|
| [31] |
SCHELLER J, STAROSSEK U. Wind tunnel tests on active flutter control by twin rotor damper[C]//Proceedings of the 13th International Conference on Wind Engineering. Amsterdam: Elsevier, 2011: 532-537. |
| [32] |
BÄUMER R, TERRILL R, STAROSSEK U.
Alternating the twin rotor damper between two modes of ope ration to eliminate small vibrations[J]. Procedia Engineering, 2017, 199: 1592–1597.
DOI:10.1016/j.proeng.2017.09.064
|
| [33] |
ZHANG Y, LI L, ZHANG X.
Switch control of twin rotor damper for bridge vibration mitigation under different excitations[J]. Procedia Engineering, 2017, 199: 1707–1712.
DOI:10.1016/j.proeng.2017.09.378
|
| [34] |
SPENCER B F, NAGARAJAIAH S.
State of the art of structural control[J]. ASCE Journal of Structural Engineering, 2003, 129(7): 845–856.
DOI:10.1061/(ASCE)0733-9445(2003)129:7(845)
|
| [35] |
ZHANG Y, LI L Y, CHENG B W, et al.
An active mass damper using rotating actuator for structural vibration control[J]. Advance in Mechanical Engineering, 2016, 8(7): 1–9.
|
| [36] |
高丙团, 贾智勇, 陈宏钧, 等.
TORA的动力学建模与Back-stepping控制[J]. 控制与决策, 2007, 22(11): 1284–1288.
DOI:10.3321/j.issn:1001-0920.2007.11.017 GAO Bingtuan, JIA Zhiyong, CHEN Hongjun, et al. Dynamical modeling and backstepping control of TORA[J]. Control and Decision, 2007, 22(11): 1284–1288. DOI:10.3321/j.issn:1001-0920.2007.11.017 |
| [37] |
XU R, ÖZGÜNER Ü.
Sliding mode control of a class of underactuated systems[J]. Automatica, 2008, 44(1): 233–241.
DOI:10.1016/j.automatica.2007.05.014
|
| [38] |
ZHIHONG M, YU X H.
Terminal sliding mode control of MIMO linear systems[J]. IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 2002, 44(11): 1065–1070.
|
| [39] |
XIN M, BALAKRISHNAN S N.
A new method for suboptimal control of a class of nonlinear systems[J]. Optimal Control Applications & Methods, 2005, 26(2): 55–83.
|
| [40] |
PENG H, WANG X, LI M, et al.
An hp symplectic pseudospectral method for nonlinear optimal control[J]. Communications in Nonlinear Science & Numerical Simulation, 2017, 42: 623–644.
|
 2018, Vol. 50
2018, Vol. 50


