旋翼作为直升机的主要气动力部件,其气动特性不仅直接影响到直升机的飞行性能,还在很大程度上影响了直升机的噪声水平和振动水平。因此,旋翼空气动力学特性的研究对于直升机的进一步发展至关重要。CFD方法充分利用了计算机技术和空气动力学理论的发展成果,可以大大地节约成本,缩短研发周期,同时可以方便地获得整个流场的信息,帮助科研工作者更好地理解旋翼流场的演化。基于RANS方程的CFD方法已经逐渐成为流场计算和气动性能预测的主要手段[1]。
旋翼存在着旋转、挥舞、摆振、变距等复杂的运动,而且桨尖涡对直升机整体的气动特性以及噪声水平有重要的影响,这使得旋翼相对于固定翼的流场模拟在一定程度上更为复杂,是旋翼CFD技术相对滞后的主要原因[2]。目前国际上很多学者采用嵌套网格技术来处理桨叶的运动[2-13]。招启军等人采用结构嵌套网格技术来进行直升机旋翼流场的研究[2-4],这一方法既可以较好地贴合桨叶的外形,又能很方便地处理桨叶的运动。但是随着桨叶形状以及直升机外形变得越来越复杂,继续采用结构网格技术来进行旋翼流场模拟的话,人为的工作量将会变得越来越大,而非结构网格能够很好地处理该问题。田书玲等人采用了非结构嵌套网格技术对旋翼流场进行了研究[5-7]。但是,相对于结构网格或者笛卡尔网格,在达到相同模拟效果的情况下,使用非结构网格技术所需要的网格数量将会很大。Shaw等人利用Landgrebe桨尖涡模型计算出了桨尖涡和涡面的位置,在生成非结构的时候在对应位置上生成较密的网格[8]。这种预加密方式提高了悬停状态下求解器对桨尖涡等流动细节的模拟效果。但是这种方式对于前飞等状态显得灵活性较差。叶靓对背景网格进行了自适应技术的研究[9],但其只能对背景网格进行自适应加密,不能进行自适应疏化。除此之外,其工作对背景网格的自适应操作没有做到全程的自适应,故没有充分地利用自适应网格的优势。Wissink等人在桨叶附近采用了非结构网格,在远离桨叶的背景网格上采用了自适应的笛卡尔结构网格[10-12],这种方式充分利用了非结构网格和自适应网格的优点,但是自适应结构网格技术需要进行网格单元的汇聚、不同网格块之间的插值等操作,汇聚的过程会使得网格数量增加,不同网格块之间的数值传递可能会引入数值误差。Harris等人在自适应的笛卡尔网格上求解涡守恒形式的N-S方程[13],但是还没有用在直升机CFD仿真上,而且算法需要通过涡量场求解速度场,使得算法的复杂度有所增加。Peron等人采用了结构化的近桨叶网格和自适应的背景网格[14],如前所述,结构化的近桨叶网格对于处理越来越复杂的桨叶、机身等部件会遇到一定的麻烦。
对此,本文针对旋翼流场模拟的复杂性,提出了适合于格心格式求解器的非结构嵌套网格算法和网格间插值方式,并且采用自适应网格技术对桨尖涡进行全程的自适应捕捉。算例结果表明,本文的方法对于旋翼流场模拟具有很好的效果,对桨尖涡等流动细节的捕捉效果比较好。本文方法可以用在桨涡干扰、旋翼机身干扰、外挂物投放等方面,具有一定的工程及科研价值。
1 旋翼运动的非结构嵌套网格 1.1 旋翼混合网格生成非结构网格可以很容易地贴合复杂的几何外形,故本文在桨叶附近生成非结构网格。为了较好地模拟桨叶物面附近的流动,本文在桨叶附近生成棱柱形的附面层网格,第一层网格的厚度为2.0×10-6,满足本文旋翼转速下桨尖位置处y+ < 10的要求。在棱柱形网格的外层,采用阵面推进法生成四面体网格[15]。生成的网格在离散精度范围内完全贴合了桨叶的外形,可以较好地反映桨叶的真实形状。
1.2 非结构嵌套网格方法相对于结构嵌套网格技术,非结构的嵌套网格技术发展较晚,没有结构嵌套网格技术发展成熟,其中自动网格装配、宿主单元搜索、网格间插值等关键技术需要通过高效的算法来实现[5-7, 16]。
1.2.1 物面距的求解在进行非结构网格的嵌套之前,需要先求解出物面距,而且物面距的求解对于k-ω SST湍流模型的计算也是必须的。对于非结构网格物面距的求解,最直接的实现是通过蛮力算法,但是算法的时间复杂度为O(NvNs),其中Nv表示体网格的数量,Ns表示物面网格的数量,这对于网格数量很大的三维算例来说,计算量过大。Tucker等人[17]研究了基于Possion方程的物面距计算方法,使计算量降低到O(NvlgNs),但是要进行微分方程的求解,增加了问题的复杂性。Wigton[18]的做法则是对网格进行分区,通过分支查找的方法减少查询次数,其计算量为O(NvNs0.5),当网格数量很大时,计算量会迅速地增加。为此,本文采用了文献[5, 16]中基于阵面推进技术的物面距求解方法,算法的时间复杂度为O(NvlgNs)。
为了保证嵌套过程的顺利进行,需要人为地为背景网格设置物面距[5],本文设置背景网格的物面距为1C, 其中C表示弦长。
1.2.2 非结构网格嵌套结合本文格心格式的求解器,对文献[5, 16, 19]中的非结构嵌套网格技术进行改进,得到非结构网格的算法如下:
(1) 根据桨叶的外形生成贴体的非结构网格。
(2) 计算各个子网格的物面距和网格尺度。
(3) 循环每一套网格里面的单元,在剩余网格里面寻找宿主单元,如果存在,则比较网格活动属性的分类参数,从而进行分类;否则,判断此单元是否落在物体内部,如果落在物体内部,此单元设置为非活动单元;否则,此单元必定是落在另一套网格的外面,需进一步根据其他网格上的宿主单元与此单元的分类参数来进行分类。
(4) 将上述各个网格上面的活动单元向前推进一层,得到传递信息的边界单元。
其中,分类参数的表达式为
| $ s = {d^p}{h^q} $ | (1) |
式中:d表示单元的格心到物面的距离;对于三维情况,
由于本文采用了格心格式的CFD求解器,如果按照文献[5]中的数值传递方式,需要将格心上的数据插值到格点上,然后再按照文献中的方式进行数值传递。在此过程中,将物理量从格心插值到格点上将会有数值误差,并且还得给每一个节点分配辅助变量的空间,操作不方便。基于此,本文采用了基于梯度的网格间数值传递方式。
单元上梯度的求解采用Green-Gauss方法,即
| $ \nabla {U_I} = \frac{1}{\mathit{\Omega }}\sum\limits_{i = 1}^{{N_F}} {\frac{1}{2}\left( {{U_I} + {U_i}} \right){\mathit{\boldsymbol{n}}_{Ii}}\Delta {S_{Ii}}} $ | (2) |
式中:
| $ {U_p} = {U_I} + \nabla {U_I}{\mathit{\boldsymbol{r}}_{Ip}} $ | (3) |
式中:Up表示边界单元p上的物理量;UI表示p单元的宿主单元I上的物理量;
由于黏性项的计算需要用到每个单元上的物理量的梯度,所以此种插值方式没有产生额外的计算量,而且在梯度计算的时候用到了当前单元相邻单元的信息,插值方式为二阶精度,满足本文求解器的精度要求。
2 全程自适应的嵌套网格系统根据旋翼CFD模拟的特点,本文在桨叶附近生成贴体的非结构网格,整个区域采用笛卡尔网格,以便于自适应加密或者疏化网格。
2.1 背景网格初始化本文采用八叉树的数据结构来处理背景网格,这样可以很方便地检索到单元的相邻单元,也可以快速地进行网格的加密与稀疏操作[20-22]。
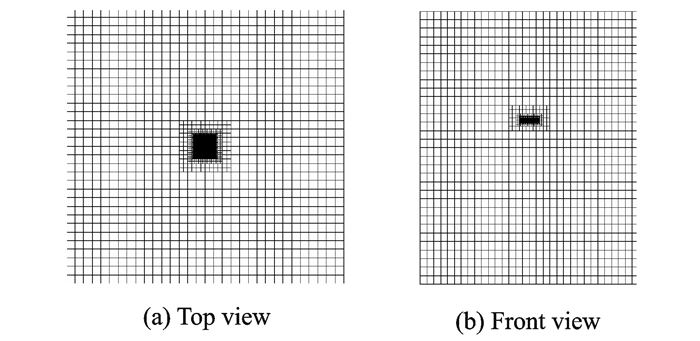
本文初始的背景网格在桨叶附近比较密(下文称为“预加密区域”),在其余的区域比较稀疏。对预加密区域网格疏化尺寸有一定的限制,即此区域的背景网格的最大尺寸为初始时刻此区域的网格尺寸。这样可以保证随着时间的推进,网格的嵌套能够顺利地进行。背景网格示意图如图 1所示。
|
图 1 初始背景网格示意 Figure 1 Original background grid |
2.2 网格自适应
网格自适应的判据形式比较多[22]。考虑到桨尖涡在很大程度上决定了直升机的气动力、诱导速度以及整机模型中对其他部件的干扰,是旋翼CFD流场模拟中一个很关键的物理量,本文采用了根据涡量对背景网格进行自适应操作的方式[22-23]。网格的自适应判据为
| $ \begin{array}{*{20}{c}} {{\mathit{\Omega }_l} = \left| \mathit{\Omega } \right|{{\left( {\sqrt {{V_i}} } \right)}^{\frac{{r + 1}}{r}}}}\\ {{\sigma _v} = \sqrt {\frac{{\sum\limits_{i = 1}^N {\mathit{\Omega }_i^2} }}{N}} } \end{array} $ | (4) |
式中:Ω表示此单元的涡量;Vi表示此单元的体积;r为确定的参数,对于三维的情况r取2;N为单元的数量。
对网格自适应处理的原则为:
(1) 如果Ωl>frσv,则对此单元进行自适应的加密处理。
(2) 如果Ωl < fcσv,则对此单元进行自适应的疏化处理。
其中:fr,fc分别表示自适应加密和自适应疏化系数,其取值将会影响到网格最终的加密、疏化效果。一般1 < fc < 3,0.1 < fc < 1,本文fr取2.0,fc取0.3。
本文在求解CFD主控方程的时候,每推进一定的时间步就进行网格的自适应处理,以随时适应桨尖涡的变化。
频繁的自适应加密操作过程中会产生的大量重复点,这可以通过交替数字树算法(Alternating digital tree, ADT)[24]进行快速地删除。对于稀疏过程中产生的大量无用点则通过标记, 删除, 移动算法(Mark, delete, move,MDM)进行删除:
(1) 建立一个辅助数组node_flag(Nnode),用于标记对应的节点是否使用过,初始化为0,其中Nnode表示现有的点的数量。
(2) 遍历八叉树上的所有叶子单元,给相应的node_flag赋值,即node_flag(IJ)= 1。其中IJ表示第I个单元的第J个顶点的编号。
(3) 在存储节点的数组中将node_flag标记为0的节点删除,同时修正八叉树上叶子单元的顶点编号。
上述算法的时间复杂度为O(Nnode),可以高效地删除自适应稀疏过程中产生的大量无用点。
3 非定常流场求解 3.1 流场控制方程N-S方程的守恒形式为
| $ \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{W}}{\rm{d}}\mathit{\Omega }} + \oint_{\partial \mathit{\Omega }} {\left( {{\mathit{\boldsymbol{F}}_c} - {\mathit{\boldsymbol{F}}_v}} \right){\rm{d}}S} = \int_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}\mathit{\Omega }} $ | (5) |
式中:W为守恒变量;Fc为对流通量;Fv为黏性项;Q为源项,对于旋翼流场模拟Q为0。W, Fc,Fv分别表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho v}\\ {\rho w}\\ {\rho E} \end{array}} \right],{\mathit{\boldsymbol{F}}_c} = \left[ {\begin{array}{*{20}{c}} {\rho {V_r}}\\ {\rho u{V_r} + {n_x}P}\\ {\rho v{V_r} + {n_y}P}\\ {\rho w{V_r} + {n_z}P}\\ {\rho HV} \end{array}} \right]}\\ {{\mathit{\boldsymbol{F}}_c} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{xx}}{n_x} + {\tau _{xy}}{n_y} + {\tau _{xz}}{n_z}}\\ {{\tau _{yx}}{n_x} + {\tau _{yy}}{n_y} + {\tau _{yz}}{n_z}}\\ {{\tau _{zx}}{n_x} + {\tau _{zy}}{n_y} + {\tau _{zz}}{n_z}}\\ {{\mathit{\Theta }_x}{n_x} + {\mathit{\Theta }_y}{n_y} + {\mathit{\Theta }_z}{n_z}} \end{array}} \right]} \end{array} $ | (6) |
式中:ρ为密度;u, v, w分别表示x, y, z方向上的速度分量;E,H分别表示单位质量总能量和总焓;Vr表示流体相对于面元的法向速度;nx, ny, nz分别表示面元的单位法向量在x, y, z方向上的分量;Vt表示逆变速度;τij为黏性张量分量;Θi为黏性应力功和流体热传导的组合项。
为了较好地模拟可能存在的气流分离现象,本文采用k-ω SST湍流模型[25],其积分型控制方程为
| $ \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {{\mathit{\boldsymbol{W}}_T}} + \oint_{\partial \mathit{\Omega }} {\left( {{\mathit{\boldsymbol{F}}_{c,T}} - {\mathit{\boldsymbol{F}}_{v,T}}} \right){\rm{d}}s} = \int_\mathit{\Omega } {{\mathit{\boldsymbol{Q}}_T}{\rm{d}}\mathit{\Omega }} $ | (7) |
式中:WT为守恒变量项;Fc, T, Fv, T为通量项;QT为源项。
3.2 方程离散为了验证本文全程自适应嵌套网格方法对流场细节的模拟效果,本文采用了简单的Jameson中心差分格式的有限体积法来计算N-S方程中的对流通项,每个面元上的对流项的计算为
| $ {\left( {{\mathit{\boldsymbol{F}}_c}\Delta S} \right)_{ij}} = {\mathit{\boldsymbol{F}}_c}\left[ {\frac{1}{2}\left( {{\mathit{\boldsymbol{W}}_i} + {\mathit{\boldsymbol{W}}_j}} \right),{\mathit{\boldsymbol{n}}_{ij}}} \right]\Delta {S_{ij}} - {\mathit{\boldsymbol{D}}_{ij}} $ | (8) |
式中:i, j为面的左右单元编号;W为守恒变量;ΔSij为i, j单元公共面元的面积;nij为此面的法向量;Dij为人工耗散项。
计算黏性项所需要的梯度通过式(2)来求解。
对于时间离散采用了二阶精度的三点后向差分进行离散,得
| $ \frac{{3\mathit{\Omega }{\mathit{\boldsymbol{W}}^{n + 1}} - 4\mathit{\Omega }{\mathit{\boldsymbol{W}}^n} + \mathit{\Omega }{\mathit{\boldsymbol{W}}^{n - 1}}}}{{2\Delta t}} + \mathit{\boldsymbol{R}}\left( {{\mathit{\boldsymbol{W}}^{n + 1}}} \right) = 0 $ | (9) |
式中:Δt为物理时间步长;R为控制体边界上通量之和;n表示时间步数。对于隐式的时间离散格式采用了LU-SGS[26]迭代方法。
LU-SGS方法要进行向前和向后两次扫略
| $ \begin{array}{l} \mathit{\boldsymbol{D}}\Delta \mathit{\boldsymbol{W}}_i^1 = - \mathit{\boldsymbol{R}}_i^n - \sum\limits_{j \in L\left( i \right)} {\frac{1}{2}\left[ {{{\left( {\Delta \mathit{\boldsymbol{F}}_c^1} \right)}_j}\Delta {S_{ij}} - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {r_A^ * } \right)}_j}\mathit{\boldsymbol{\bar I}}\Delta \mathit{\boldsymbol{W}}_j^1} \right]\\ \mathit{\boldsymbol{D}}\Delta \mathit{\boldsymbol{W}}_i^n = \mathit{\boldsymbol{D}}\Delta \mathit{\boldsymbol{W}}_i^1 - \sum\limits_{j \in U\left( i \right)} {\frac{1}{2}\left[ {{{\left( {\Delta \mathit{\boldsymbol{F}}_c^n} \right)}_j}\Delta {S_{ij}} - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {r_A^ * } \right)}_j}\mathit{\boldsymbol{\bar I}}\Delta \mathit{\boldsymbol{W}}_j^n} \right] \end{array} $ | (10) |
式中:
| $ \mathit{\boldsymbol{D}} = \left( {\frac{\mathit{\Omega }}{{\Delta \tau }} + \frac{\omega }{2}{{\mathit{\bar \Lambda }}_c} + {{\mathit{\bar \Lambda }}_v}} \right)\mathit{\boldsymbol{I}} - \frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial \mathit{\boldsymbol{W}}}}\mathit{\Omega } $ |
| $ \mathit{r}_A^ * = \omega {{\bar \lambda }_c} + {{\bar \lambda }_v},\omega \in \left( {1,2} \right] $ |
| $ {{\mathit{\bar \Lambda }}_c} = \sum {{{\bar \lambda }_c}} = \sum {\rho \left( {\frac{{\partial {\mathit{\boldsymbol{F}}_c}}}{{\partial \mathit{\boldsymbol{W}}}}} \right)} $ |
| $ {{\mathit{\bar \Lambda }}_v} = \sum {{{\bar \lambda }_v}} = \sum {\rho \left( {\frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial \mathit{\boldsymbol{W}}}}} \right)} $ |
运用LU -SGS迭代法前要对网格进行重排,以提高收敛效率和稳定性。运用湍流模型时,湍流方程源项中的耗散项进行隐式处理,以增强对角矩阵的对角占优,提高迭代求解代数方程的稳定性,源项中其他部分则采用显式处理[27]。
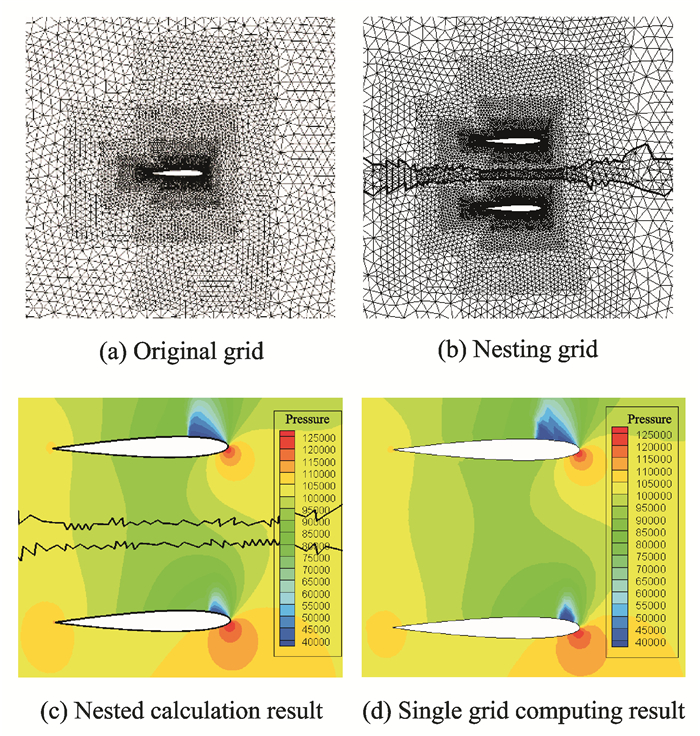
4 算例及计算结果分析 4.1 二维双翼型计算为了便于示意本文嵌套网格技术的可行性,本文使用简单的二维嵌套网格结果来示意非结构嵌套网格的计算效果。初始的网格是采用文献[15]中的方法生成非结构网格,如图 2(a)所示。将第二套网格向下平移距离1之后将两套网格进行嵌套处理。由嵌套之后的网格示意图(图 2(b))可以看出,本文所采用的嵌套网格技术可以很好地将两套网格分割开来。
|
图 2 双翼型嵌套计算示意 Figure 2 Result of double airfoil |
计算了在来流马赫数为0.6,迎角为7.4°情况下的流场情况。图 2(c)是在本文求解器中使用嵌套网格得到的结果,其中的两条黑线分别表示两套网格的边界。图 2(d)是在Fluent软件中使用单块网格得到的计算结果。可以看出,在采用嵌套网格技术得到的结果中,压力等值线在网格交界处过渡得比较平滑,流场的压力等值线分布与图 2 (d)的结果相当,这验证了本文所采用的嵌套算法和基于梯度的插值方法合理。
4.2 Car adonna&Tung旋翼悬停计算为验证本文的方法对旋翼悬停流场模拟的能力,本文算例采用了NASA的Caradonna&Tung实验旋翼[28]。该旋翼的实验结果已经在衡量旋翼CFD模拟效果中得到了广泛的应用。该旋翼半径为1.143 m,弦长为0.190 5 m,采用了NACA0012翼型,桨叶无负扭转和尖削,跟切长度为0.190 5 m。
本文在桨叶附近生成贴体的非结构网格,每片桨叶附近的网格数量约62万个。背景网格采用了非结构网格和笛卡尔网格两种网格形式,嵌套结果对比如图 3,4所示。

|
图 3 非结构背景网格与近桨叶网格的嵌套示意 Figure 3 Overset grid based on unstructured grids |
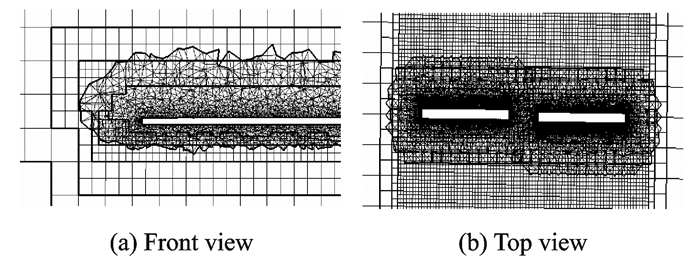
|
图 4 笛卡尔背景网格与近桨叶网格的嵌套示意 Figure 4 Overset grid based on unstructured grids and Cartesian grids |
由图 3, 4可以看出,不管对于全部是非结构网格的网格系统,还是对于笛卡尔网格与非结构网格混合的网格系统,本文的非结构网格嵌套方法都能很好地把桨叶网格和背景网格区分开来,而且顺利进行了网格间的嵌套操作。从而证明了本文非结构网格方法的可行性与普适性。
为了采用自适应网格技术,本文接下来的计算只展示了背景网格是笛卡尔网格的情况。初始的背景网格比较稀疏,网格数量约31万个,以尽可能地减少不必要的计算资源的消耗。
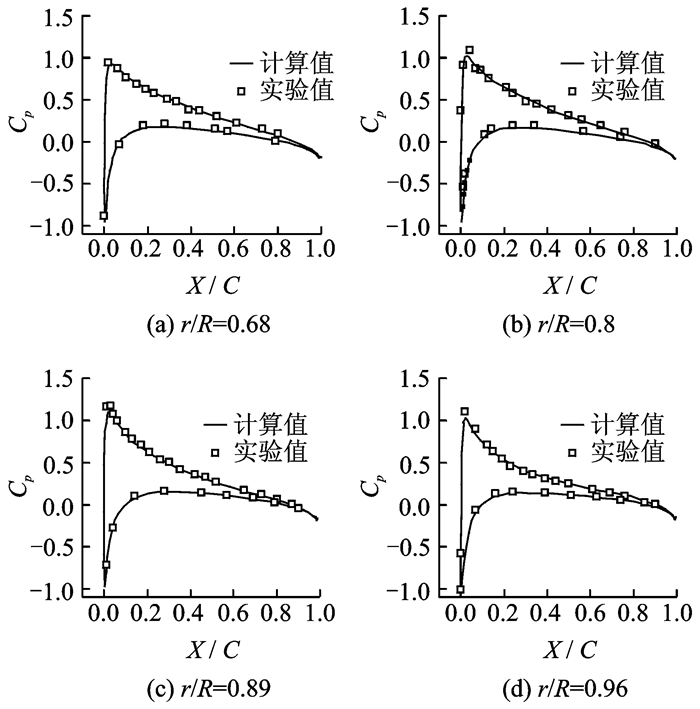
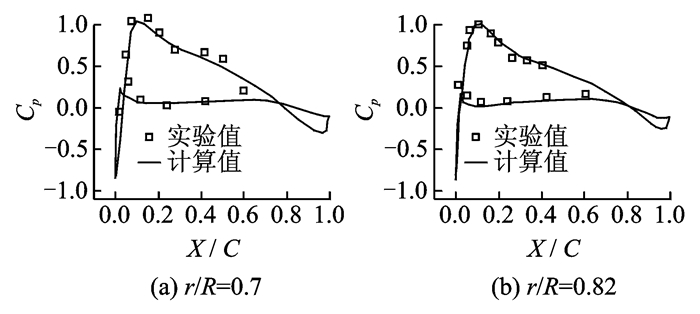
4.2.1 截面压力系数分布Caradonna&Tung旋翼的计算条件为:桨尖马赫数0.439,桨距角8°,处于悬停状态。图 5给出了不同截面处压力系数的分布与实验值的对比。可以看出,本文计算结果与实验值吻合较好,证明本文所采用的方法可行。
|
图 5 Caradonna & Tung旋翼截面压力系数分布 Figure 5 Comparison of computed surface pres sure with experimental data of Caradonna & Tung rotor |
4.2.2 自适应之后的网格分布
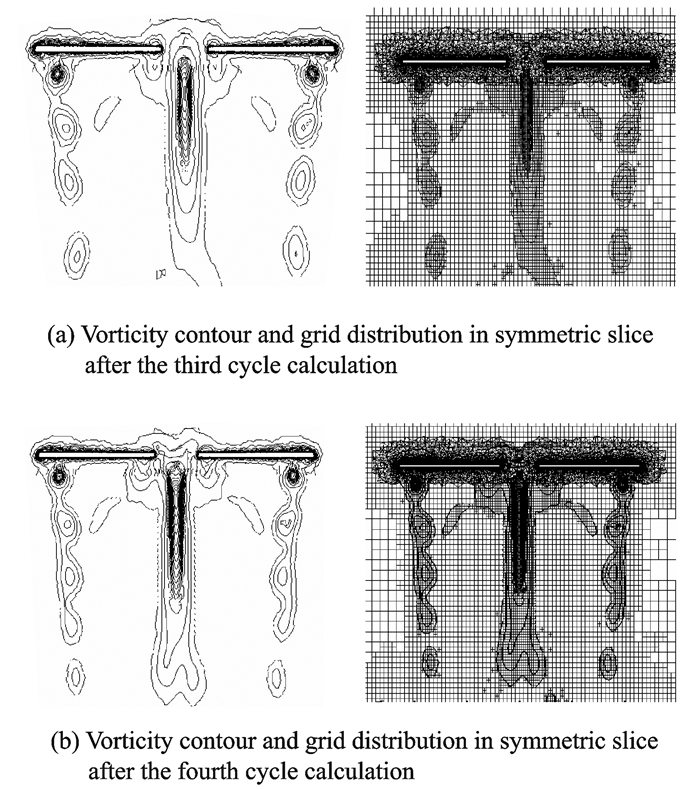
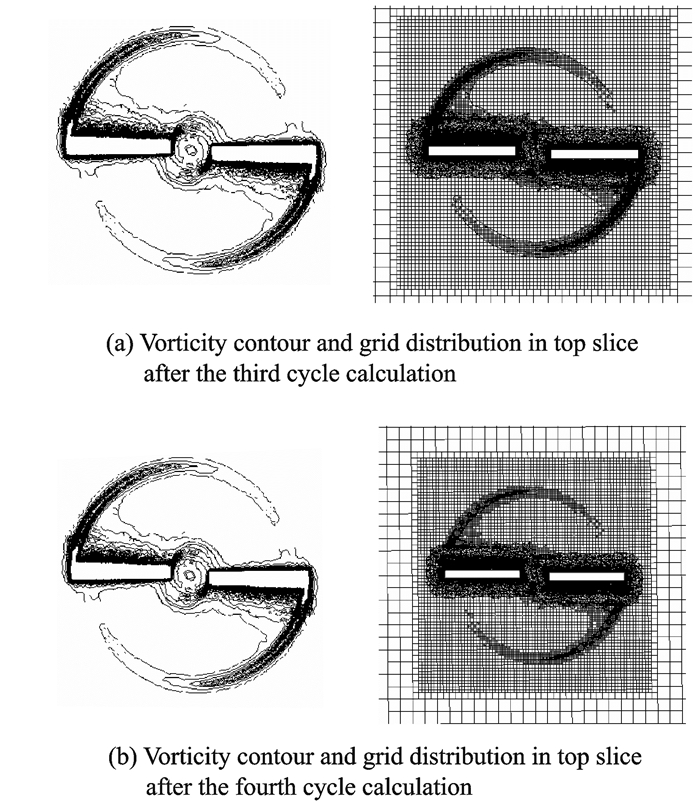
图 6,7显示了第3圈和第4圈计算结束之后对称截面和顶部截面上涡量等值线分布以及相应的网格分布,其中第3圈和第4圈计算结束之后对应的状态分别进行了300次和400次自适应操作。
|
图 6 Caradonna & Tung旋翼对称截面上的涡量等值线与网格分布 Figure 6 Vorticity c ontour and grid distribution in symmetric slice of Caradonna & Tung rotor |
|
图 7 Caradonna & Tung旋翼顶部截面上涡量等值线与网格分布 Figure 7 Vorticity contour and grid di stribution in top slice of Caradonna & Tung rotor |
从图 6,7可以看出,本文的自适应网格能够很好地跟随涡量的变化,适合于捕捉桨尖涡等流动细节。
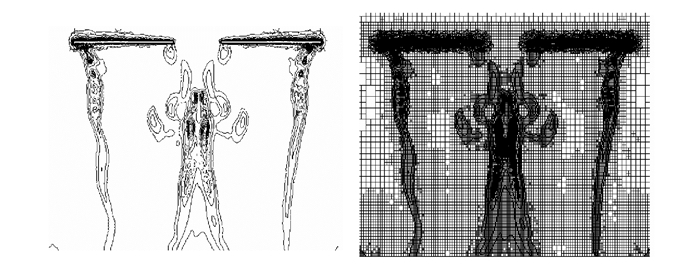
4.2.3 桨尖涡的模拟效果图 8显示了在没有采用自适应网格技术和采用自适应网格技术的情况下求解器对桨尖涡捕捉效果的对比。可以看出,采用自适应网格技术之后,求解器对桨尖涡的捕捉效果得到了很大的提升,而且捕捉到了传统涡流理论中的中央涡束。表明本文的自适应网格系统对模拟旋翼流场的可行性与有效性。

|
图 8 Caradonna & Tung旋翼自适应前后涡量捕捉效果对比 Figure 8 Blade tip vortex before and after self-adaption of Caradonna & Tung rotor |
由于在全程自适应的过程中采用了相应的自适应疏化操作,网格的数量不至于过大,不会占用过多的计算资源,在计算结束之后,背景网格的数量约为103万个。
4.3 HLISHAPE 7A旋翼悬停计算本算例使用了有实验结果可以对照的HELISHAPE 7A旋翼[29]。该旋翼有4片桨叶,每片桨叶半径2.1 m,弦长0.14 m,桨叶平面形状为矩形。需要注意的是,该旋翼采用了先进桨叶布置,桨叶分为3段,每段具有不同的翼型剖面,且有非常规的几何扭转。计算状态为来流马赫数0,即悬停状态,桨距角为5.97°,桨尖马赫数为0.617。
在桨叶附近生成贴体的非结构网格,每片桨叶附近的网格数量约67万个,初始的背景网格数量约64万个。
4.3.1 截面压力系数分布图 9展示了在上述悬停状态下桨叶截面的压力分布与实验值的对比情况,可以看出计算结果与实验值吻合较好。再一次说明了本文的全程自适应非结构嵌套网格系统对于模拟旋翼流场是合理的。
|
图 9 HLISHAPE 7A旋翼截面压力系数分布 Figure 9 Comparison of computed surface pressure with expe rimental data of HLISHAPE 7A rotor |
4.3.2 自适应之后的网格分布
图 10, 11展示了计算结束之后对称截面和顶部截面上的涡量分布以及相应的网格分布。
|
图 10 HLISHAPE 7A旋翼对称截面上的涡量等值线和网格分布 Figure 10 Vorticity contour and grid distributio n in symmetric slice of HLISHAPE 7A rotor |
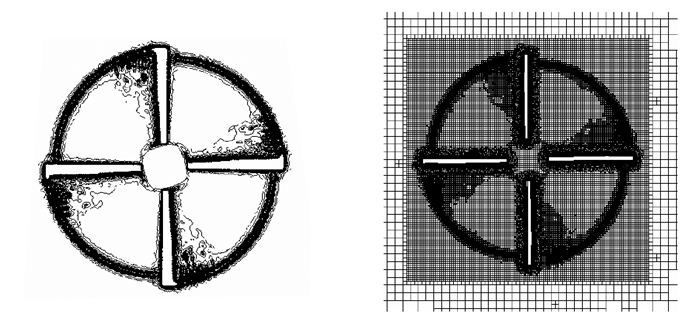
|
图 11 HLISHAPE 7A旋翼顶部截面上涡量等值线与网格分布 Figure 11 Vorticity contour and grid distribution in top slice of HLISHAPE 7A rotor |
从图 10, 11可以看出,本文的自适应网格系统在桨尖涡存在的空间位置进行了很好的加密,这对于桨尖涡捕捉精度及流场求解效果的提升是有利的。
此算例计算结束的时候背景网格的数量约为685万个。相比之前的Caradonna & Tung旋翼,背景网格的数量增加了很多,主要原因是:
(1) 本算例中的桨叶展弦比比较大,使得在背景网格上设定的预加密区域比较大,因此网格的数量有所增加。
(2) 由于此旋翼采用4片桨叶,相对于之前的算例,对于每个时刻,桨尖涡存在的空间范围较大,由式(4)可知需要加密的网格数量会增加,对比图 6, 10及图 7,11也可以明显地看出来。
5 结论针对旋翼流场模拟的复杂性,改进并提出了适合于格心格式求解器的非结构嵌套网格算法和网格间插值方法;采用全程自适应非结构嵌套网格方法对旋翼流场的进行模拟,充分利用了非结构网格适应性强和自适应网格精度高、灵活性好的特点;对于频繁自适应过程中产生的重复点和无用点采用ADT算法和MDM算法予以高效的删除。主要结论如下:
(1) 二维、三维算例验证了本文针对格心格式的求解器所提出的非结构嵌套网格算法和网格间插值方法的有效性。
(2) 通过ADT算法和MDM算法高效地删除频繁自适应过程中产生的大量重复点和无用点,节约了不必要的计算资源的消耗。
(3) 本文采用的基于梯度的网格间插值方式可以利用相邻单元的信息,插值满足二阶精度,同时不需要额外的存储空间和计算资源的消耗,是一种比较适合于格心格式求解器的网格间插值方法。
(4) 在旋翼流场模拟的全过程中都进行网格的自适应操作,可以随时适应桨尖涡的变化,提高了对桨尖涡等流动细节的捕捉精度,同时对计算资源的占用不至于过大。计算算例表明,本文方法具有很好的鲁棒性与有效性,可以应用在桨涡干扰、旋翼机身干扰及舰载等方面。
| [1] |
BLAZEK J.
Computational fluid dynamics:Principles and applications (Second Edition)[M]. London: Elsevier, 2005: 1-4.
|
| [2] |
徐国华, 招启军.
直升机旋翼计算流体力学的研究进展[J]. 南京航空航天大学学报, 2003, 35(3): 338–344.
DOI:10.3969/j.issn.1005-2615.2003.03.023 XU Guohua, ZHAO Qijun. Advances in computational fluid dynamics of helicopter rotor[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2003, 35(3): 338–344. DOI:10.3969/j.issn.1005-2615.2003.03.023 |
| [3] |
赵国庆, 招启军, 吴琪.
旋翼非定常气动特性CFD模拟的通用运动嵌套网格方法[J]. 航空动力学报, 2015, 30(3): 546–554.
ZHAO Guoqing, ZHAO Qijun, WU Qi. A universal moving-embedded grid method for CFD simulation of unsteady aerodynamic characteristics of rotot[J]. Journal of Aerospace Power, 2015, 30(3): 546–554. |
| [4] |
李亚波. 基于自适应网格方法的倾转旋翼流场数值模拟[D]. 南京: 南京航空航天大学, 2013.
LI Yabo. Numerical simulations for flowfield of tilt-rotor based on adaptive grid method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. |
| [5] |
田书玲. 基于非结构网格方法的重叠网格算法研究[D]. 南京: 南京航空航天大学, 2008.
TIAN Shuling. Investigation of overset unstructured grids algorithm[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. |
| [6] |
许和勇, 叶正寅, 王刚, 等.
基于非结构嵌套网格的旋翼前飞流场计算[J]. 西北工业大学学报, 2006, 24(6): 763–767.
DOI:10.3969/j.issn.1000-2758.2006.06.020 XU Heyong, YE Zhengyin, Wang Gang, et al. Improving numerical simulation of rotor forward flight flow field with unstructured dynamic overset grids[J]. Journal of Northwestern Polytechnical University, 2006, 24(6): 763–767. DOI:10.3969/j.issn.1000-2758.2006.06.020 |
| [7] |
许和勇, 叶正寅, 史爱明.
基于非结构嵌套网格的旋翼-机身干扰流场数值模拟[J]. 西北工业大学学报, 2010, 28(6): 814–817.
DOI:10.3969/j.issn.1000-2758.2010.06.002 XU Heyong, YE Zhengyin, SHI Aiming. An effective method for numerically simulating helicopter rotor-fuselage aerodynamic interference using unstructured overset grids[J]. Journal of Northwestern PolytechnicalUniversity, 2010, 28(6): 814–817. DOI:10.3969/j.issn.1000-2758.2010.06.002 |
| [8] |
SHAW S T, HILL J L, VILLAMARIN C E M. A priori grid adaptation for helicopter rotor wakes using unstructured and structured-unstructured hybrid grids[C]//43rd AIAA Aerospace Science Meeting and Exhibit. Reno, Nevada: AIAA, 2005. |
| [9] |
叶靓. 基于非结构网格的直升机旋翼流场及噪声研究[D]. 南京: 南京航空航天大学, 2009.
YE Liang. Research on the flowfield and noise of helicopter rotors based on unstructured mesh[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. |
| [10] |
WISSINK A M, KAMKAR S, PULLIAM T H, et al. Cartesian adaptive mesh refinement for rotorcraft wake resolution[C]//28th AIAA Applied Aerodynamics Conference. Chicago, Lllinois: AIAA, 2010. |
| [11] |
WISSINK A M, JAYARAMAN B, DATTA A, et al. Capability enhancements in version 3 of the helios high-fidelity rotorcraft simulation code[C]//50th AIAA Aerospace Science Meeting Including the New Horizons Forum and Aerospace Exposition. Nashville, Tennessee: AIAA, 2012. |
| [12] |
WISSINK A M, KATZ A J, SITARAMAN J. Validation of 3D RANS-SA calculations on Strand/Cartesian meshes[C]//52nd Aerospace Sciences Meeting. National Harbor, Maryland: AIAA, 2014. |
| [13] |
AIAA. An efficient adaptive cartesian vorticity transport solver for rotorcraft flowfield analysis[C]//AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. [S. l. ]: AIAA, 2010. |
| [14] |
PERON S, BENOIT C.
Automatic off-body overset adaptive Cartesian mesh method based on an octree approach[J]. Journal of Computational Physics, 2013, 232(1): 153–173.
DOI:10.1016/j.jcp.2012.07.029
|
| [15] |
MCMORRIS H, KALLINDERIS Y.
Octree-advancing front method for generation of unstructured surface and volume meshes[J]. AIAA Journal, 1997, 35(6): 976–984.
DOI:10.2514/2.206
|
| [16] |
LOHNER R.
Applied computational fluid dynamics techniques[M]. Chichester, UK: John Wiley & Sons Ltd, 2008.
|
| [17] |
TUCKER P G, RUMSEY C L, BARTELS R E, et al. Transport equation based wall distance computations aimed at flows with time-dependent geometry[R]. NASA/TM-2003-212680, 2003. |
| [18] |
WIGTON L. Research in computational aeroscience applications implemented on advanced parallel computing systems[R]. NASA/CR-96-206062, 1996. |
| [19] |
NAKAHASHI K, TOGASHI F, SHAROV D.
An inter grid-boundary definition method for overset unstructured grid approach[J]. AIAA Journal, 2000, 38(11): 2077–2084.
DOI:10.2514/2.869
|
| [20] |
WANG Z J, CPHEN R F, HARIHARAN N, et al.
A 2N tree bases automated viscous Cartesian grid methodology for feature capturing[J]. AIAA Journal, 1999: 99–3300.
|
| [21] |
COIRIER W J, POWELL K G. Adaptively refined Euler and Navier-Stokes solutions with a Cartesian-cell based scheme[C]//ICASE/LaRC Workshop on Adaptive Grid Methods. [S. l. ]: [s. n. ], 1995: 153-161. |
| [22] |
COIRIER W J. An adaptively-refined, Cartesian, cell-based scheme for the Euler and Navier-Stokes equations[D]. Ann Arbor: The University of Michigan, 1994. |
| [23] |
招启军, 徐国华.
直升机计算流体动力学基础[M]. 北京: 科学出版社, 2016: 120-128.
|
| [24] |
BONET J, PERAIRE J.
An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems[J]. International Journal for Numerical Methods in Engineering, 1991, 31(1): 1–17.
DOI:10.1002/(ISSN)1097-0207
|
| [25] |
MENTER F R.
Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598–1605.
DOI:10.2514/3.12149
|
| [26] |
JAMESON A, TURKEL E.
Implicit schemes and MYMLUMYM decompositions[J]. Mathematics of Computation, 1981, 37(156): 385–397.
|
| [27] |
WILCOX D C.
Turbulence modeling for CFD[M]. California, USA: DCW Industries, 2006: 363-367.
|
| [28] |
CARADONNA F X, TUNG C.
Experimental and analytical studies of a model helicopter rotor in hover[J]. Vertica, 1981, 5(1): 149–161.
|
| [29] |
STEIJL R, BARAKOS G N, BADCOCK K J. A CFD framework for analysis of helicopter rotors[C]//17th AIAA Computational Fluid Dynamics Conference. Toronto, Ontario, Canada: AIAA, 2005. |
 2018, Vol. 50
2018, Vol. 50


