2. 南京航空航天大学能源与动力学院, 南京, 210016
2. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China
汽车主动安全控制是减少交通事故的重要措施之一,众多学者对此深入研究以提高车辆行驶稳定性,并取得了大量的实用成果,如制动系统(Anti-lock braking system,ABS),直接横摆力矩控制(Direct yaw m oment control,DYC),电子稳定程序(Electronic stability program,ESP),主动前轮转向(Active front steering,AFS)等,这些系统的实车装备极大改善了车辆的行驶安全性。ABS, DYC, ESP等控制系统是控制车轮的纵向受力来改善车辆的稳定性,AFS是通过给前轮施加一个独立于驾驶员的附加转角改变车轮的横向受力来改善车辆的操纵稳定性。
PID控制在工业控制中有着广泛的应用,由于不便于提取系统的微分信号,在实际控制中常用比例微分(Proportion integrati on, PI)控制,其对于线性系统具有良好的控制效果。如果把车辆动力学系统作为线性系统,采用PI控制技术设计主动前轮控制器是一个不错的选择,如PI反馈控制器[1-3]、自适应模糊PI控制器[4]用于跟踪横摆角速度。但是,PI控制器不但参数难以调节,而且用于非线性控制系统的鲁棒性不高。而车辆动力学系统亦是一个高度的非线性系统,存在建模误差、参数摄动和外部干扰这些因素影响闭环控制系统性能。滑模控制(Sliding mode control, SMC)对于系统不确定性及外部扰动具有良好的鲁棒性,且不需要精确的数学模型,广泛应用于车辆的主动安全控制。如文献[5-8]采用传统的线性滑模面设计AFS控制器,跟踪车辆的横摆角速度和质心侧偏角,但线性滑模控制在无限时间内收敛于零点,且控制器的输出存在振颤。文献[9-11]把终端滑模控制(Terminal sliding mode, TSM)用于AFS控制器设计,在有限时间收敛于零点,控制器输出不存在振颤问题,但存在奇异问题。为避免控制器奇异,同时加快远离滑模面状态的收敛速度,设计了非奇异终端滑模控制(Non-singular terminal sliding mode, NTSM),如文献[12-13]分别设计了跟车控制系统与液位跟踪控制系统,都取得了良好的控制效果。
扩张状态观测器(Extended state observer, ESO)能及时估计车辆状态和系统扰动,并对扰动进行补偿,则ESO与NTSM结合能提高NTSM控制器的性能。本文提出基于ESO与非奇异终端滑模控制的主动前轮转向系统,ESO估计系统的各阶状态,NTSM跟踪车辆理想横摆角速度,控制车辆横向稳定性。
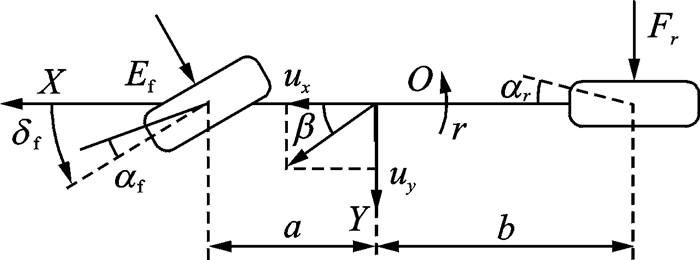
1 车辆主动前轮转向系统 1.1 二自由度车辆模型忽略悬架的影响,不考虑载荷变化对轮胎特性和回正力矩的影响,则车辆模型可以简化为线性二自由度模型,如图 1所示。该模型常用于研究车辆的侧向运动和横摆运动。如果忽略车速的变化,且前轮转角较小,则式(1)动力学方程描述车辆二自由度模型为
| $ \left\{ \begin{array}{l} \dot r = \frac{{{a^2}{C_1} + {b^2}}}{{{I_z}{u_x}}}r + \frac{{a{C_1} - b{C_2}}}{{{I_z}}}\beta - \frac{{a{C_1}}}{{{I_z}}}{\delta _{\rm{f}}}\\ \dot \beta = \left( {\frac{{a{C_1} - b{C_2}}}{{mu_x^2}} - 1} \right)r + \frac{{{C_1} + {C_2}}}{{m{u_x}}}\beta - \frac{{{C_1}}}{{m{u_x}}}{\delta _{\rm{f}}} \end{array} \right. $ | (1) |
|
图 1 车辆二自由度模型 Figure 1 2-DOF model of vehicle |
式中:m为汽车质量;Iz为绕Z轴的转动惯量,其中,Z为过坐标系原点O且垂直于X轴和Y轴确定的平面,方向向上;r为横摆角速度;β为质心侧偏角;C1,C2分别为前后轴侧偏刚度;a,b分别为质心到前后轴的距离;δf为前轮转角;ux为车辆前进速度。
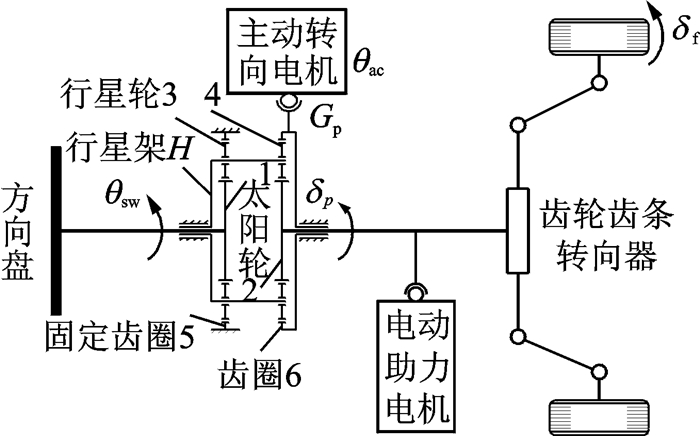
1.2 主动前轮转向车辆模型线控转向系统(Steering by wir e,SBW)能实现主动转向,但由于法规要求转向盘与前轮必须通过机械进行连接,故目前SB W系统未实用于商用车;另一种主动转向系统是通过给前轮施加一个独立于驾驶员的前轮转角实现的,典型的有宝马公司的2自由度行星齿轮机构转向器,奥迪公司的谐波齿轮机构转向器等。本文研究主动前轮转向系统[14],如图 2所示。齿轮齿条转向器输入为δp(行星齿轮机构输出),由θsw和主动转向电机转角θac叠加得到。
|
图 2 主动前轮转向系统组成 Figure 2 AFS system |
式(1)描述车辆模型中的前轮转角δf=δsw+δac,其中δsw由转向盘转角θsw产生(δsw=θsw/G,G为车辆转向系统传动比),δac由主动转向电机转角θac产生。
| $ {\delta _{\rm{p}}} = {\theta _{{\rm{sw}}}} - \frac{{{Z_6}}}{{{Z_1}{G_{\rm{p}}}}}{\theta _{{\rm{ac}}}} $ | (2) |
式中:Gp为主动转向电机与齿圈6之间蜗轮蜗杆机构传动比,Z1, Z6分别为太阳轮与齿圈6的齿数。
由式(2)可知
| $ {\delta _{{\rm{ac}}}} = - \frac{{{Z_6}}}{{{Z_1}{G_{\rm{p}}}G}}{\theta _{{\rm{ac}}}} $ | (3) |
通过控制θac的大小与方向实现主动转向,同时实现转向系统传动比可变。
2 ESO与NTSM控制器 2.1 扩张状态观测器ESO基本理论扩张状态观测器ESO首先由韩京清提出[15],特别适用于估计存在模型与参数误差、外部扰动的非线性系统状态,赵志良证明了ESO的收敛性[16]。对于非线性系统,有
| $ {y^{\left( n \right)}} = f\left( {y,\dot y, \cdots ,{y^{\left( {n - 1} \right)}},t} \right) $ | (4) |
式中:
如果将变量y(n)也当作状态变量, 则得到被扩张的状态变量
| $ \left\{ \begin{array}{l} {{\dot {\hat x}}_1} = {{\hat x}_2} - {\beta _{01}}{g_1}\left( e \right)\\ \;\;\;\;\;\;\;\;\;\; \vdots \\ {{\dot {\hat x}}_n} = {{\hat x}_{n + 1}} - {\beta _{0n}}{g_n}\left( e \right)\\ {{\dot {\hat x}}_{n + 1}} = - {\beta _{0,n + 1}}{g_{n + 1}}\left( e \right) \end{array} \right. $ | (5) |
式中
文献[15]指出,选取适当非线性函数g1,…,gn+1和系数β0,1,…,g0, n
+1,则此系统各状态分别跟踪被扩张的状态变量
| $ {{\hat x}_1} \to y, \cdots ,{{\hat x}_n} \to {y^{\left( {n - 1} \right)}},{{\hat x}_{n + 1}} \to {y^{\left( n \right)}} $ |
考虑式(1)系统为主动前轮转向系统,对式(1)两边求导,并整理其第1个方程,则
| $ \ddot r = f\left( {r,\dot r,{a_y}} \right) + B{{\dot \delta }_{\rm{f}}} $ | (6) |
式中:ay为侧向加速度;
| $ \begin{array}{*{20}{c}} {f\left( {r,\dot r,{a_y}} \right) = \frac{{{a^2}{C_1} + {b^2}{C_2}}}{{{I_z}{u_x}}}\dot r - \frac{{a{C_1} - b{C_2}}}{{{I_z}}}r + }\\ {\frac{{a{C_1} - b{C_2}}}{{{I_z}{u_x}}}{a_y}} \end{array} $ |
令
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = f\left( {r,\dot r,{a_y},{{\dot \delta }_{{\rm{sw}}}}} \right) + B{{\dot \delta }_{{\rm{ac}}}}\\ y = {x_1} \end{array} \right. $ | (7) |
式(7)由线性二自由度系统推导得来,而实际上车辆是一个高度的非线性系统,
| $ \left\{ \begin{array}{l} e = {z_1} - {y^ * }\\ {{\dot z}_1} = {z_2} - {\beta _1} \cdot e\\ {{\dot z}_2} = {z_3} - {\beta _2} \cdot {\rm{Fal}}\left( {e,\xi ,\Delta } \right) + B{{\dot \delta }_{{\rm{ac}}}}\\ {{\dot z}_3} = - {\beta _3} \cdot {\rm{Fal}}\left( {e,{\xi _1},{\Delta _1}} \right) \end{array} \right. $ | (8) |
适当选择式(8)中增益β1, β2, β3以及非线性函数Fal,则z1→x1,z2→x2,z3→x3。非线性函数Fal可以采用不同的形式,本文中Fal表达式为[17]
| $ {\rm{Fal}}\left( {e,\xi ,\Delta } \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\left| e \right|^\xi }{\rm{sign}}\left( e \right)\\ e{\Delta ^{\xi - 1}} \end{array}&\begin{array}{l} \left| e \right| > \Delta \\ \left| e \right| \le \Delta \end{array} \end{array}} \right. $ | (9) |
式中,ξ和Δ为正数。
2.3 非奇异终端滑模控制器NTSM设计滑模变结构控制对系统的模型误差和外扰具有良好的鲁棒性,广泛应用于非线性系统的控制。其中,TSM由于在有限时间内收敛以及改善了控制器输出的“抖振”问题,能取代传统线性滑模控制SMC成为研究热点[18-19]。文献[20]对终端到达律进行设计,使控制律完全消除负指数项,从而解决了TSM控制的奇异问题,同时进一步改善“抖振”。文献[21]构造了带状态高次项的非奇异快速终端滑模函数,设计了终端吸引子得到连续且无负指数项的滑模控制律。本文结合ESO与文献[21]的NTSM控制方法对车辆主动前轮转向进行控制。
针对式(7)所描述系统,设计其滑模面与终端吸引子[21],则
| $ \left\{ \begin{array}{l} s = {x_1} + \frac{1}{\alpha }x_1^{g/h} + \frac{1}{\beta }x_2^{p/q}\\ \dot s = \left( { - \varphi s - \gamma {s^{m/n}}} \right)x_2^{p/q - 1} \end{array} \right. $ | (10) |
式中:α,β为正实数; g,h,p,q,m,n为正奇数,且满足1 < p/q,0 < m/n < 1。
则式(7)的控制律
| $ u = - \frac{{\beta q}}{p}\left[ {\left( {\varphi s + \gamma {s^{\frac{m}{n}}}} \right) + x_2^{2 - \frac{p}{q}}\left( {1 + \frac{g}{{\alpha h}}{x_1}^{\frac{g}{h} - 1}} \right)} \right] - {x_3} $ | (11) |
式(11)时间连续无负指数项,避免了控制奇异及控制律抖振。式中
| $ u = - \frac{{\beta q}}{p}\left[ {\left( {\varphi s + \gamma {s^{\frac{m}{n}}}} \right) + z_2^{2 - \frac{p}{q}}\left( {1 + \frac{g}{{\alpha h}}{z_1}^{\frac{g}{h} - 1}} \right)} \right] - {z_3} $ | (12) |
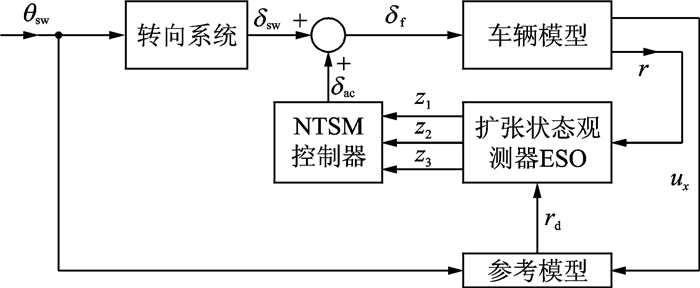
|
图 3 主动前轮转向控制结构 Figure 3 Control structure of AFS |
NTSM控制器控制输入为扩张状态观测器ESO估计的车辆状态,ESO的输入为车辆实际横摆角速度r与参考横摆角速度rd,控制器的输出为前轮附加转角。参考横摆角速度rd为
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {r_{\rm{d}}} = \frac{{{u_x}{\theta _{{\rm{sw}}}}}}{{L\left( {1 + Ku_x^2} \right)G}}\\ {r_{\rm{d}}} = \frac{{\mu g}}{{{u_x}}} \end{array}&\begin{array}{l} \left| {{r_{\rm{d}}}} \right| < \frac{{\mu g}}{{{u_x}}}\\ \left| {{r_{\rm{d}}}} \right| \ge \frac{{\mu g}}{{{u_x}}} \end{array} \end{array}} \right. $ | (13) |
式中:K为不足转向系数;μ为道路附着系数;L为车辆轴距;g为重力加速度。
3 ESO与NTSM控制仿真试验本文在Matlab软件中搭建NTSM控制器,控制CarSim非线性车辆模型(CS B-CLASS)进行仿真验证NTSM的控制效果。分别进行抗外扰、参数摄动和路径跟踪试验,并对两种控制器(PID和NTSM)的试验结果进行分析。车辆模型主要参数见表 1,控制器参数见表 2。
| 表 1 车辆模型主要参数 Table 1 Main parameters of vehicle model |
| 表 2 控制器参数 Table 2 Controller parameters |
3.1 抗外扰试验
工况:车辆直线行驶,有随机横向风的外界扰动,横向风模型如图 4所示;试验车速ux=80 km/h,道路附着系数0.85。
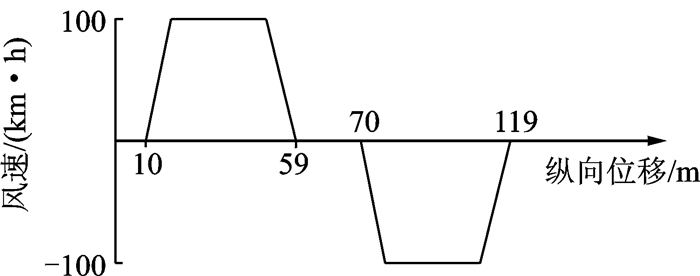
|
图 4 随机横向风 Figure 4 Random crosswind |
图 5为主动转向车辆在随机横向风作用下直线行驶仿真试验结果。在图 4横向风的干扰下,无控制车辆偏离直线路径较严重,PID和NTSM控制车辆路径偏离均得到有效抑制。在整个试验过程中,无控制车辆侧向路径偏离最大达2 m,PID控制车辆侧向路径偏离最大达0.73 m,而NTSM控制侧向偏离最大为0.45 m,NTSM控制对外界干扰具有明显的抑制作用,效果好于PID控制。
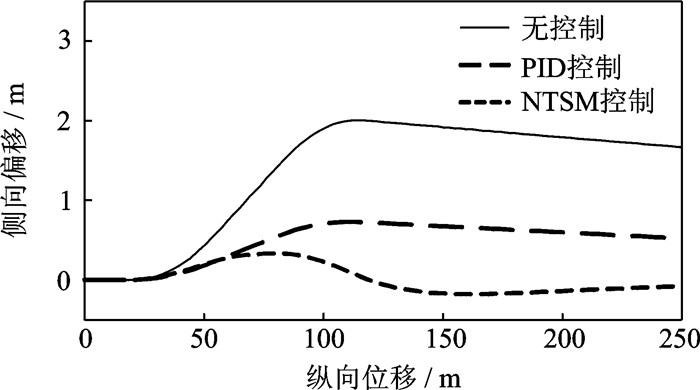
|
图 5 车辆抗外扰试验 Figure 5 Test of vehicle resistance to external disturbance |
3.2 高附着路面路径跟踪试验
工况:双移线试验预期路径设置[22-23]如图 6所示。附着系数为0.85;车速为ux=100 km/h。
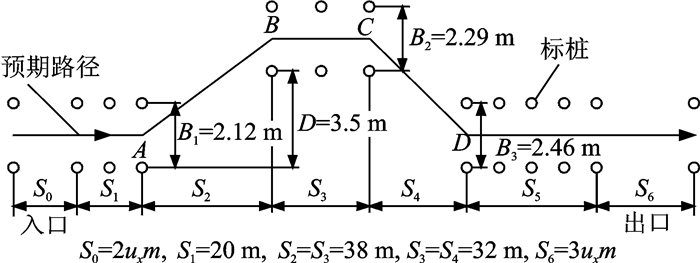
|
图 6 双移线试验路径设置 Figure 6 Double lane change test path setting |
图 7是高附着路面双移线仿真试验路径跟踪结果。NTSM控制效果明显,能较好完成双移线试验,PID控制亦能完成双移线试验,但路径跟踪性能不如NTSM控制,而无控制车辆存在较大偏离。在试验结束回到直线段,NTSM控制车辆超调量为0.12 m,PID控制车辆超调量为0.29 m,无控制车辆超调量为0.38 m,表明NTSM控制能明显抑制超调。
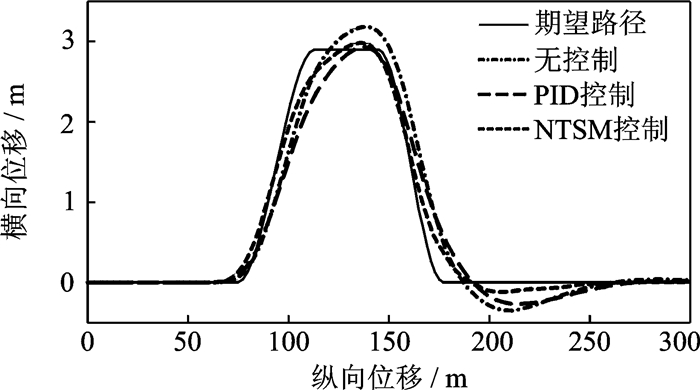
|
图 7 双移线试验车辆行驶轨迹(高附着) Figure 7 Vehicle track of double lane change test(high-μ) |
图 8是高附着路面双移线试验车辆横摆角速度响应。PID控制能改善横摆角速度跟踪性能,而NTS M控制对横摆角速度跟踪性能好于PID控制。
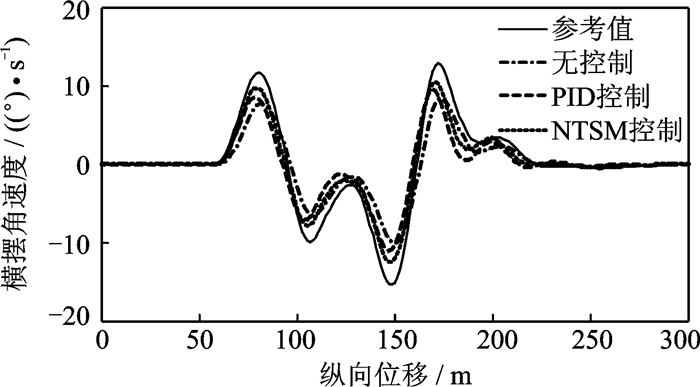
|
图 8 双移线试验横摆角速度响应(高附着) Figure 8 Yaw rate response of double lane change test(high-μ) |
3.3 低附着路面路径跟踪试验
低附着路面双移线试验工况除路面附着系数为0.3,其他与高附着路面双移线试验工况一致。
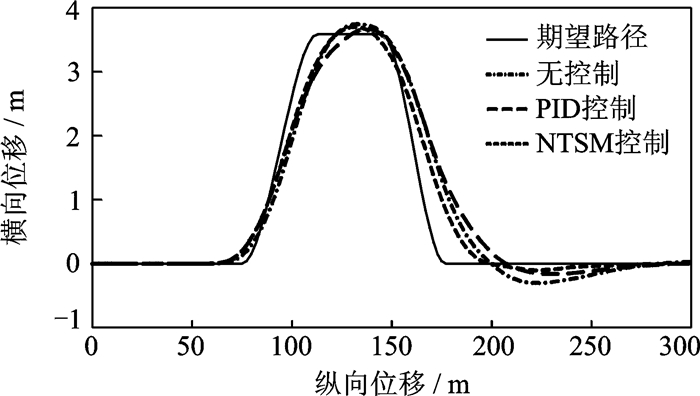
图 9是低附着路面双移线试验车辆行驶轨迹。图 9表明,在低附着路面上有与高附着路面上相似的试验结果,主动前轮转向控制车辆各种性能优于未控制车辆。其中,NTSM控制优于PID控制,有较好的路径跟踪和抑制超调的性能。
|
图 9 双移线试验车辆行驶轨迹(低附着) Figure 9 Vehicle track of double lane change test(low-μ) |
图 10是低附着路面上双移线试验横摆角速度响应。横摆角速度的极限值由路面附着系数决定,超过极限值车辆将发生侧滑。图 10试验结果表明,在部分时段,未控制车辆的横摆角速度响应超出极限值较多,车辆将发生侧滑;PID控制横摆角速度响应亦有超出极限值现象,但超出数值较小;而NTSM控制车辆横摆角速度响应在极限值内。
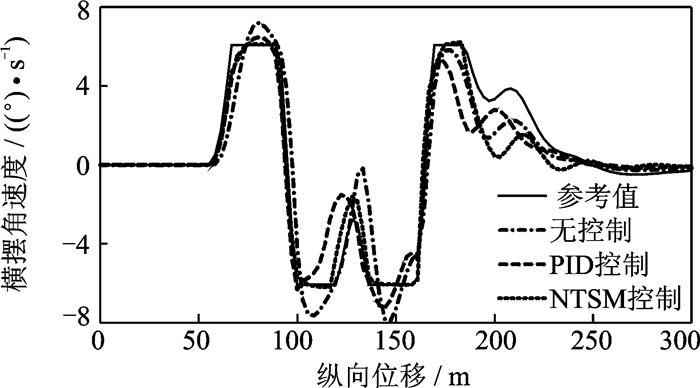
|
图 10 双移线试验横摆角速度响应(低附着) Figure 10 Yaw rate response of double lane change test(low-μ) |
高、低附着路面双移线试验表明,NTSM控制车辆具有好的路径跟踪、横摆角速度跟踪性能,能够把横摆角速度响应控制在极限范围内。所以,NTSM控制的主动前轮转向系统提高了车辆的操纵稳定性和行驶安全性。
3.4 车辆参数变化的影响改变试验车辆模型的总质量,其他参数不变,同时控制器参数不变。车辆总质量增加(增加的质量用百分比表示):0%, 25%, 50%, 75%和100%,各种工况仿真试验结果如图 11所示。NTSM控制器能控制车辆较好完成试验,跟踪轨迹略有变化,在回到直线段(S5, S6),其超调量随质量的增加而增大。试验结果表明控制器对车辆质量参数的变化具有鲁棒性。
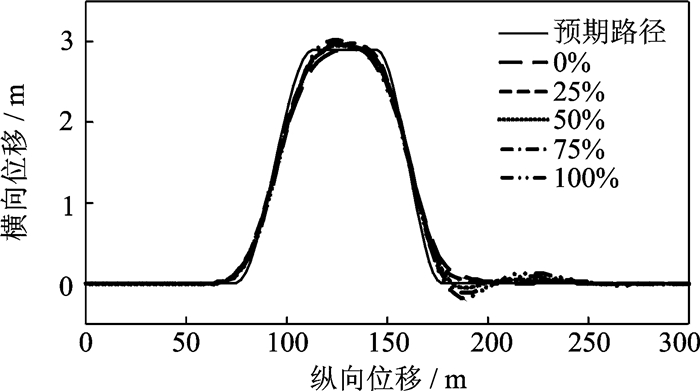
|
图 11 车辆质量参数变化对控制器性能影响 Figure 11 Influence of vehicle quality parameters change on controller performance |
实际上,一般随质量的变化,车辆的质心位置会发生变化,前后桥垂直载荷的变化又会引起轮胎侧偏刚度的变化;车辆是一个复杂的非线性系统,采用线性二自由度车辆模型设计控制器,还存在未建模误差。因此,上述试验结果表明NTSM控制器对车辆的内扰(未建模误差,参数摄动等)具有较好的鲁棒性。
4 结束语文章提出的基于ESO与NTSM的主动前轮转向控制器实现车辆实际横摆角速度跟踪理想横摆角速度,控制车辆横摆角速度响应于安全阈值内,提高了车辆的操纵稳定性。仿真试验结果表明,NTSM控制具有较强的抗内外干扰的能力,跟踪性能良好,控制器本身鲁棒性好。而且NTSM控制器设计过程中未针对具体的数学模型和具体问题,其可移植性好,但控制器参数较多,存在参数调制不易的问题,同时还应指出的是AFS系统是通过改变车辆的横向受力进行主动控制,因此,AFS与其他通过改变车辆纵向受力进行主动安全控制的系统,如直接横摆力矩控制DYC等进行集成,能进一步改善车辆的操纵稳定性。
| [1] |
LI Q, SHI G, WEI J, et al. Yaw stability control of active front steering with fractional-order PID controller[C]//International Conference on Information Engineering and Computer Science. [S. l]: IEEE, 2009: 1-4. |
| [2] |
WANG L, LIU G, ZHANG D, et al. Integrated control of active front steering and direct yaw moment for multi-wheel independently driven electric vehicles[C]//International Conference on Electrical Machines and Systems. [S. l]: IEEE, 2014: 2301-2304. |
| [3] |
DIAO Xiaoyan, JIN Yang, MA Li, et al.
Composite active front steering controller design for vehicle system[J]. IEEE Access, 2017, 5: 6697–6706.
DOI:10.1109/ACCESS.2017.2693687
|
| [4] |
KADIR Z, MAZLAN S, ZAMZURI H, et al.
Adaptive fuzzy-PI control for active front steering system of armoured vehicles:Outer loop control design for firing on the move system[J]. Journal of Mechanical Engineering, 2015, 61(3): 187–195.
DOI:10.5545/sv-jme
|
| [5] |
AKAR M, KALKKUHL J C.
Lateral dynamics emulation via a four-wheel steering vehicle[J]. Vehicle System Dynamics, 2008, 46(9): 803–829.
DOI:10.1080/00423110701632925
|
| [6] |
DING S, LIU L, ZHENG W X.
Sliding mode direct yaw-moment control design for in-wheel electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6752–6762.
DOI:10.1109/TIE.2017.2682024
|
| [7] |
TIAN W, ZHANG C, QIAN C, et al.
Global stabilization of inherently nonlinear systems using continuously differentiable controllers[J]. Nonlinear Dynamics, 2014, 77(3): 739–752.
DOI:10.1007/s11071-014-1336-y
|
| [8] |
TIAN W, DU H, QIAN C.
A generalized homogeneous solution for global stabilization of a class of non-smooth upper-triangular systems[J]. International Journal of Control, 2014, 87(5): 951–963.
DOI:10.1080/00207179.2013.862347
|
| [9] |
ZHOU Q, YAO D, WANG J, et al.
Robust control of uncertain semi-Markovian jump systems using sliding mode control method[J]. Applied Mathematics and Computation, 2016, 286: 72–87.
DOI:10.1016/j.amc.2016.03.013
|
| [10] |
DING S, LI S.
Second-order sliding mode controller design subject to mismatched term[J]. Automatica, 2017, 77: 388–392.
DOI:10.1016/j.automatica.2016.07.038
|
| [11] |
CHEN Jansong, CHEN Nan, YIN Guodong.
4-wheels vehicle sliding mode robust stability control considering the nonlinear characteristics[J]. Journal of Southeast University, 2010, 40(5): 969–972.
|
| [12] |
李升波, 李克强, 王建强, 等.
非奇异快速的终端滑模控制方法及其跟车控制应用[J]. 控制理论与应用, 2010, 27(5): 543–550.
LI Shengbo, LI Keqiang, WANG Jianqiang, et al. Nonsingular fast terminal-sliding-mode control method and its application on vehicular following system[J]. Control Theory & Applications, 2010, 27(5): 543–550. |
| [13] |
赵鹏, 姚敏立, 沈晓卫, 等.
非奇异快速终端滑模液位跟踪控制[J]. 西安交通大学学报, 2011, 45(12): 39–44.
ZHAO Peng, YAO Minli, SHEN Xiaowei, et al. Tracking control of water level based on a nonsingular fast terminal sliding mode[J]. Journal of Xi'an Jiaotong University, 2011, 45(12): 39–44. |
| [14] |
魏建伟. 主动转向控制机理及其干预时EPS系统转向路感研究[D]. 南京: 南京航空航天大学, 2011.
WEI Jianwei. Research on control mechanism of active steering and steering feeling of EPS system with the interference of active steering[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011. |
| [15] |
韩京清.
一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995, 10(1): 85–88.
DOI:10.3321/j.issn:1001-0920.1995.01.020 HAN Jingqing. The extended state observer of a class of uncertain systems[J]. Control and Decision, 1995, 10(1): 85–88. DOI:10.3321/j.issn:1001-0920.1995.01.020 |
| [16] |
赵志良. 非线性自抗扰控制的收敛性[D]. 合肥: 中国科学技术大学, 2012.
ZHAO Zhiliang. Convergence of nonlinear active disturbance rejection control[D]. Hefei: University of Science and Technology of China, 2012. |
| [17] |
韩京清.
自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
HAN Jingqing. Active disturbance rejection control technique:The technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008. |
| [18] |
MAN Z, PAPLINSKI A P, WU H R.
A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators[J]. IEEE Transactions on Automatic Control, 1994, 39(12): 2464–2469.
DOI:10.1109/9.362847
|
| [19] |
FENG Y, YU X M.
Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159–2167.
DOI:10.1016/S0005-1098(02)00147-4
|
| [20] |
冯勇, 鲍晟, 余星火.
非奇异终端滑模控制系统的设计方法[J]. 控制与决策, 2002, 17(2): 194–198.
DOI:10.3321/j.issn:1001-0920.2002.02.017 FENG Yong, BAO Sheng, YU Xinghuo. Design method of non-singular terminal sliding mode control systems[J]. Control and Decision, 2002, 17(2): 194–198. DOI:10.3321/j.issn:1001-0920.2002.02.017 |
| [21] |
李升波, 李克强, 王建强, 等.
非奇异快速的终端滑模控制方法[J]. 信息与控制, 2009, 38(1): 1–8.
DOI:10.3969/j.issn.1002-0411.2009.01.001 LI Shengbo, LI Keqiang, WANG Jianqiang, et al. Nonsingular and fast terminal sliding mode control method[J]. Information and Control, 2009, 38(1): 1–8. DOI:10.3969/j.issn.1002-0411.2009.01.001 |
| [22] |
中国国家标准化管理委员会. GB/T6323-2014, 汽车操纵稳定性试验方法[S]. 北京: 中国标准出版社, 2014.
Standardization Administration of the People's Republic of China. GB/T6323-2014, controllability and stability test PROCEDURE for automobile[S]. Beijing: Standards Press of China, 2014. |
| [23] |
ISO/FDIS 3888-1, Passenger cars-Test track for a severe lane change manoeuvre-Part 1: Double lane change[S]. Geneva: International Standardization Organization, 2002. |
 2018, Vol. 50
2018, Vol. 50


