2. 江苏科技大学能源与动力工程学院, 镇江, 212003;
3. 武警后勤学院学兵二大队九队, 天津, 300309
2. College of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang, 212003, China;
3. Student 2 Brigade 9 Teams, Logistics University of PAP, Tianjin, 300309, China
与其他浮空器相比,平流层飞艇具有独特的优势,其在卫星通信、气象测量等民用领域以及监视、防御等军事领域得到广泛地应用。近年来,越来越多的国家重视平流层飞艇的发展。但是,平流层飞艇载荷舱电子设备的热控问题一直没能得到很好地解决[1]。在飞艇上升过程中,当遇到临近地面的高温环境时,如果没有相应的制冷措施则会影响设备的使用性能。另一方面,飞艇上升过程中,大气密度会不断降低,传统的空冷系统也会面临质量流量较低而带来的制冷量不足的问题。
目前已有的文献表明,仅有少数人对平流层飞艇载荷舱的热控进行了相关的研究,而且由于关键技术的保密性,许多技术成果没有对外公开[2]。另外,这些研究主要针对平流层飞艇载荷的整体热控研究,且处于起步阶段,涉及平流层飞艇载荷舱中的电子设备的热控问题较少[3]。Dumas等[4]基于欧盟所提出的MAAT平流层飞艇平台,对飞艇载荷舱的温度调节系统进行了详细的计算和分析。刘欣[5]对平流层飞行器电子设备舱热控制中涉及的相关问题进行研究,通过分析和计算,提出了通过选择辐射器安装位置来提高辐射能力的热控制思路。李大鹏[6]对平流层飞艇通信系统载荷舱进行了热控制设计,提出了一种以被动热控为主、主动热控为辅的载荷舱热控制思路,并给出了隔热、等温化、加热和液体循环回路等热控手段的具体设计方法。王旭巍等[7]提出了一种平流层飞艇电子设备舱的被动热控方案。周湘杰等[8]设计了一种平流层飞艇的流体回路控制系统。
本文提出了一种基于开放式二氧化碳制冷的设备舱电子设备冷却方案,并分析了可能造成制冷量损失的因素,使得平流层飞艇在上升过程中全高度下设备舱电子设备的温度能控制在一个合适的范围。该技术为平流层飞艇的局部热控提供了技术参考,同时对开放式二氧化碳制冷系统的使用起到推广作用。
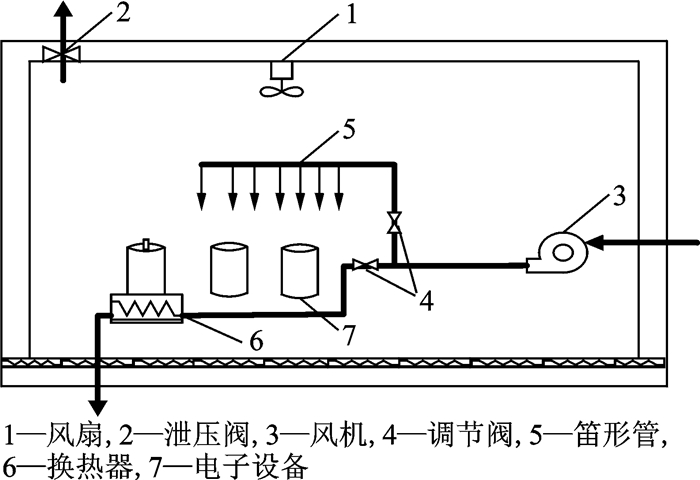
1 基于冷板的电子设备舱热设计方案考虑到平流层飞艇对电功率消耗及系统质量有严格的限制,传统的蒸发制冷循环优势并不明显,因此应充分利用周围环境的冷量对电子设备及载荷舱进行热设计。基于上述要求,对于设备舱的热控制,可采取如图 1所示的热管理方案[9]。
|
图 1 飞艇载荷舱的温控示意图 Figure 1 Thermal control system for the equipment cabin in a stratospheric airship |
如图 1所示,周围环境中的空气通过风机送入舱内,送入的空气分为两个支路,一路通过冷板对电子设备进行冷却,另一路通过笛形管对舱内进行送风。舱内设有一风扇用于控制舱内温度的均匀性。由于飞艇在上升过程中舱内外的压差是恒定的,因此舱内有一个泄压阀将舱内多余的空气排向舱外。同时,由于飞艇在20 km定点巡航时周围环境温度较低,长时间的定点巡航可能会导致舱内温度低于电子设备正常工作的温度范围,因此在舱底部装有辐射电加热膜。
上述方案存在着一定的不足,即若飞艇起飞时的地面环境温度较高,尤其是高于35 ℃时,由于舱内设备使用环境的限制,飞艇起飞阶段基于冷板制冷的电子设备散热系统将无法起到冷却的效果。同时,高空时由于外界环境的密度较低,为了满足空冷系统的设计要求,则需要较大的风机风速。然而风机的引气既要满足冷板的需求,也要满足舱内制冷的需求,因此在高空时可能会导致支路进气流量不足。综上所述,从设计可靠性的角度,应尽可能的设计一套完善的制冷系统以满足飞艇在全高度的工作要求,因此本文提出了优化的设计方案。
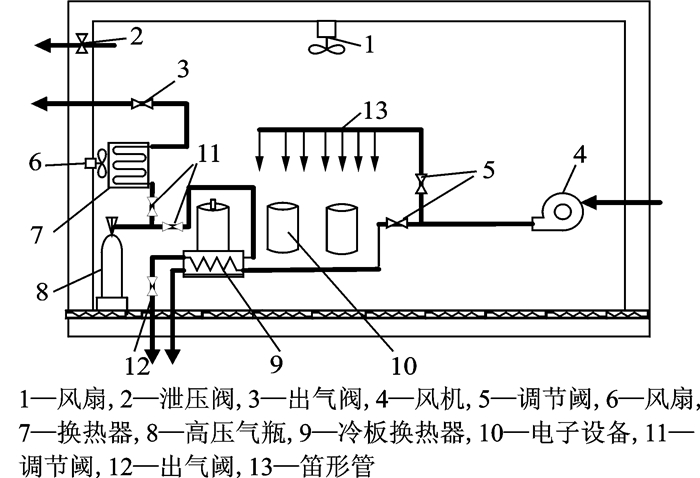
2 基于开放式二氧化碳制冷的飞艇载荷舱电子设备冷却方案本文提出了如图 2所示的一种电子设备冷却方案。其基本工作原理如下:飞艇升空过程中若遇到临近地面的高温环境,基于开放式二氧化碳制冷的温度控制子系统开启,高压储气罐中的二氧化碳制冷剂输送至冷板换热器,一支路用于冷却与之联接或靠近的电子设备,另一支路对舱内进行送风;当飞艇上升至高空风机流量不够时,可以开启基于二氧化碳制冷的温度控制子系统,此时跟基于周围空气直接送风的控制子系统共同工作。
|
图 2 基于开放式二氧化碳制冷的飞艇载荷舱电子设备冷却方案 Figure 2 Cooling system for electronic devices in a stratospheric airship cabin based on an open carbon dioxide refri geration |
需要说明的是,基于二氧化碳的电子设备冷却系统是不可逆的,设计时应根据飞艇的起飞环境、升空时间等来计算所需求的二氧化碳制冷剂的量。同时,为了研究开放式二氧化碳制冷系统的制冷特性及其影响因素,需建立开放式制冷系统的模型,并对其进行研究分析。本文主要针对该系统的制冷性能及其影响因素进行研究。
3 热设计计算模型 3.1 二氧化碳质量计算对于开放式二氧化碳制冷系统,可采用式(1) [10]对所需二氧化碳的质量进行估算
| $ m = \frac{q}{{{h_{{\rm{ex}}}} - {u_{{\rm{in}}}}}}\Delta t $ | (1) |
式中:m为所需二氧化碳的质量;q为电子设备的功率,设为200W[11];hex为二氧化碳的排气焓值,根据排气状态参数P2= 0. 055bar,T2=217.15K[11]。利用REFPROP软件计算可得hex=440.92kJ/ kg;uin为初始条件下二氧化碳的内能,根据初始状态参数P1=65bar,T1=298.15 K[12],利用REFPROP软件计算可得uin=264.79 kJ/kg;Δt为飞艇上升过程持续时间,为5094s[11]。根据以上条件及公式计算可得m=5.78kg。
出于安全因素的考虑,二氧化碳在灌装时不能灌满,必须留有一定的余量。另外,考虑到常用钢瓶的体积规格以及使用过程中的损失,本文选择体积为20L的钢瓶,充气系数α=0.6 kg/L,净重12kg。
3.2 二氧化碳制冷剂在气瓶中的状态研究为了研究二氧化碳制冷剂在气瓶中的状态,建立理论计算模型时需做如下假设[13]:
(1) 忽略气瓶瓶体的热阻;
(2) 假设制冷剂在冷板中充分换热。
根据开放式二氧化碳制冷系统中制冷剂状态的不同,其计算模型可分为单相态模型和两相态模型。
(1) 单相态模型
二氧化碳流量方程
| $ \frac{{{\rm{d}}\left( {mv} \right)}}{{{\rm{d}}t}} = 0 $ | (2) |
二氧化碳质量方程
| $ \frac{{{\rm{d}}m}}{{{\rm{d}}t}} = \frac{q}{{h - {h_{{\rm{ex}}}}}} $ | (3) |
气瓶内二氧化碳能量守恒方程
| $ \frac{{{\rm{d}}\left( {mu} \right)}}{{{\rm{d}}t}} = \alpha A\left( {{T_{{\rm{out}}}} - T} \right) + h\frac{{{\rm{d}}m}}{{{\rm{d}}t}} $ | (4) |
式中:v为二氧化碳比体积,t为单位时间,h为瓶内二氧化碳焓值,u为二氧化碳内能,α为对流换热系数,A为有效换热面积,Tout为吊舱内的温度,T为瓶内二氧化碳的温度。
(2) 两相态模型
二氧化碳质量方程
| $ \frac{{{\rm{d}}m}}{{{\rm{d}}t}} = \frac{q}{{{h_1} - {h_{{\rm{ex}}}}}} $ | (5) |
气瓶内二氧化碳能量守恒方程
| $ \frac{{{\rm{d}}\left( {mu} \right)}}{{{\rm{d}}t}} = \alpha A\left( {{T_{{\rm{out}}}} - T} \right) + {h_1}\frac{{{\rm{d}}m}}{{{\rm{d}}t}} $ | (6) |
式中hl为饱和液态二氧化碳的焓值。
3.3 状态模型求解考虑到单相态模型和两相态模型方程的相似性,本文仅针对后者进行分析。由式(2)和(6)得
| $ m\frac{{{\rm{d}}v}}{{{\rm{d}}t}} + v\frac{{{\rm{d}}m}}{{{\rm{d}}t}} = 0 $ | (7) |
| $ m\frac{{{\rm{d}}u}}{{{\rm{d}}t}} = \alpha A\left( {{T_{{\rm{out}}}} - T} \right) - \left( {u - {h_1}} \right)\frac{{{\rm{d}}m}}{{{\rm{d}}t}} $ | (8) |
将式(7,8)代入式(5)得
| $ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - \frac{v}{m} \cdot \frac{q}{{{h_1} - {h_{{\rm{ex}}}}}} $ | (9) |
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = \frac{1}{m}\left[ {\alpha A\left( {{T_{{\rm{out}}}} - T} \right) + \frac{{{h_1} - u}}{{{h_1} - {h_{{\rm{ex}}}}}}q} \right] $ | (10) |
单相态模型也可以以同样的方法计算,计算结果如下
| $ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - \frac{v}{m} \cdot \frac{q}{{h - {h_{{\rm{ex}}}}}} $ | (11) |
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = \frac{1}{m}\left[ {\alpha A\left( {{T_{{\rm{out}}}} - T} \right) + \frac{{h - u}}{{h - {h_{{\rm{ex}}}}}}q} \right] $ | (12) |
对比式(3)和式(5)可知,单相态模型和两相态模型的区别仅在于变量h和hl不一样。式(5),(9),(10)即为两相态制冷剂的状态方程,可以通过VC++编程利用二阶龙格-库塔法求解。式中的u和hl可以通过REFPROP软件进行计算。
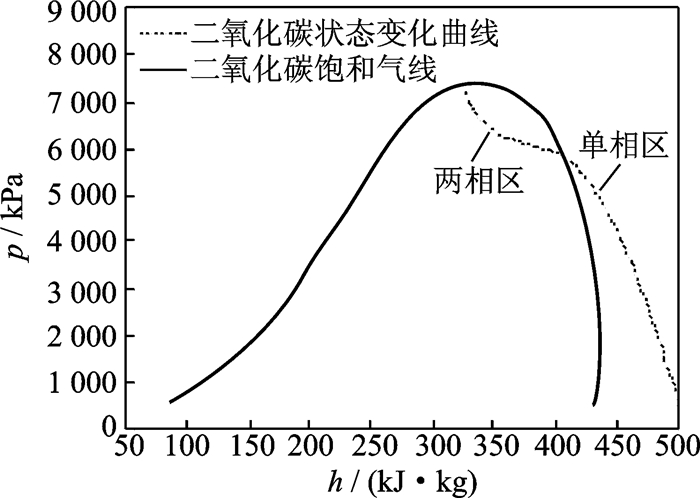
3.4 计算结果与分析以二氧化碳气瓶的储存温度30 ℃为例使用龙格库塔法对式(5),(9),(10)进行计算求解,得到如图 3所示的气瓶内二氧化碳状态变化曲线。
|
图 3 气瓶内二氧化碳状态变化曲线 Figure 3 State change of carbon dioxide in the gas cylinder |
从图 3可以看出,当气瓶内二氧化碳处于气液两相区时,曲线的斜率相对较小,气瓶内的压力相对稳定;当气瓶内二氧化碳处于单相区时,曲线的斜率急剧增大,气瓶内的压力迅速降低。分析可知,造成这种现象的主要原因是:当气瓶内二氧化碳处于两相区时,部分液态二氧化碳蒸发变成气体,使瓶内压强维持在相对稳定的状态;当气瓶内二氧化碳处于单相区时,由于此时液态二氧化碳的量相对较少或不存在液态二氧化碳,导致流出气瓶的二氧化碳无法及时补充,使得气瓶内压力迅速下降。
4 制冷量损失计算 4.1 制冷量损失原因及计算方法分析对于开放式二氧化碳制冷系统,制冷量损失主要包括两类[12]:
(1) 随着制冷剂流出气瓶,瓶内二氧化碳温度降低,导致储存温度高于气瓶内温度,气瓶与储存环境之间产生热交换,造成制冷量损失。这类制冷量损失可通过式(13)进行计算
| $ {Q_1} = \int_0^{{t_0}} {\alpha A\left( {{T_{{\rm{out}}}} - T} \right){\rm{d}}t} $ | (13) |
式中:Q1为热交换引起的制冷量损失,α为对流换热系数,A为对流换热面积,本文中指气瓶表面积,Tout为储存环境温度,T为气瓶内二氧化碳温度,t0为马赫数达到1所用的时间。
(2) 随着制冷剂流出气瓶,瓶内二氧化碳压力降低,当压力过低时,瓶内的制冷剂将无法流出气瓶,此时瓶内剩余的制冷剂将无法利用,从而产生制冷量损失。对于此类制冷量损失,可通过计算节流阀最小流通截面处的马赫数达到1时气瓶内剩余气体量来计算。计算公式如下
| $ {Q_2} = {m_{\rm{r}}}\left( {{u_{\rm{t}}} - {h_{{\rm{ex}}}}} \right) $ | (14) |
式中:Q2为剩余制冷剂导致的制冷量损失,mr为马赫数等于1时气瓶内剩余制冷剂的质量,ut为气瓶内剩余制冷剂的内能,hex为排气焓值。
4.2 制冷量损失的影响因素分析本文主要从二氧化碳气瓶的储存温度、管道直径以及排气压力三个方面对制冷量损失的影响因素进行分析。
(1) 二氧化碳气瓶的储存温度
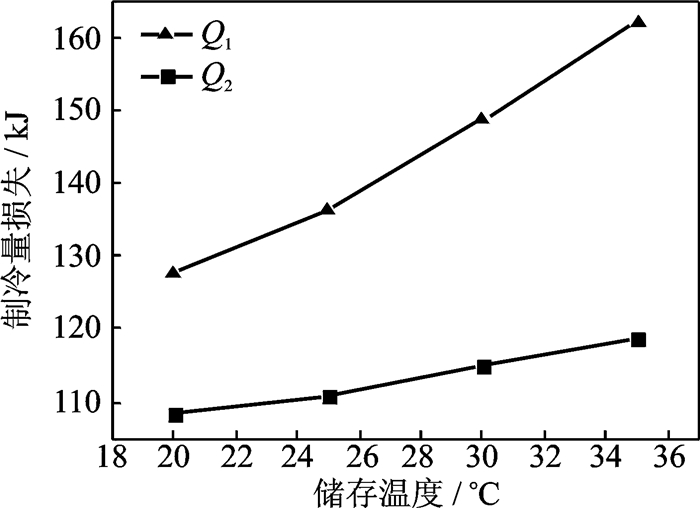
以储存温度20,25,30和35 ℃为例,计算得到不同储存温度下气瓶内二氧化碳两类制冷量损失量,如图 4所示。
|
图 4 不同储存温度下的制冷量损失 Figure 4 Cooling capacity loss for varying conditions of temperature |
由图 4可知,二氧化碳气瓶的储存温度越高,制冷量损失越大,且第一类制冷量损失要大于第二类制冷量损失;随着储存温度的增大,第一类制冷量损失曲线的斜率急剧增大,这主要是由于储存温度的增大导致气瓶内外的温差变大,从而产生较大的制冷量损失。因此,在实际设计过程中,应根据设备的最低极限温度选择较低的储存温度且在制冷过程中要对储罐进行绝热处理, 防止储罐中的冷量损失。
(2) 管道直径
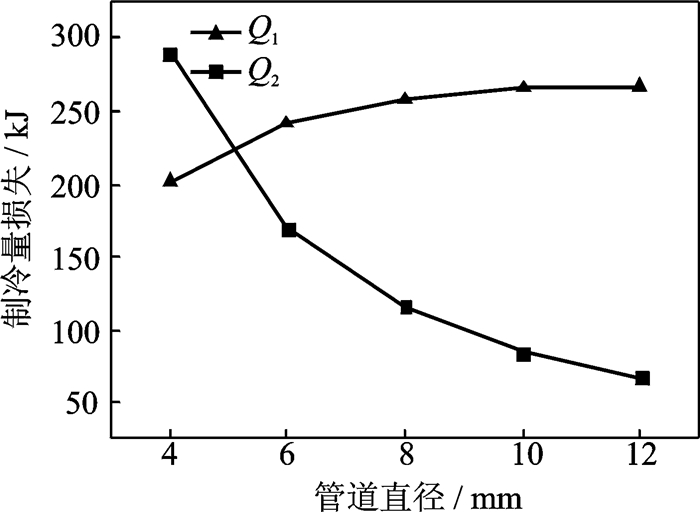
以管道直径4, 6, 8, 10和12 mm为例,计算得到不同管径下两类制冷量损失,如图 5所示。
|
图 5 不同管径下的制冷量损失 Figure 5 Cooling capacity loss for varying conditions of pipe diameter |
由图 5可知,随着管道直径的增大,第一类制冷量损失增加,第二类制冷量损失大幅减小。由公式(13)可知,当其他条件不变时,第一类制冷量损失仅与马赫数达到1所用的时间有关。当管道直径增大时,制冷剂在管道中的流动阻力增加,马赫数达到1所用的时间增大,一方面会导致第一类制冷量损失增加;另一方面,会使气瓶内剩余制冷剂减少,从而导致第二类制冷量损失减小。综合考虑以上两方面的因素,在实际设计过程中,应选择直径较大的管道。
(3) 排气压力
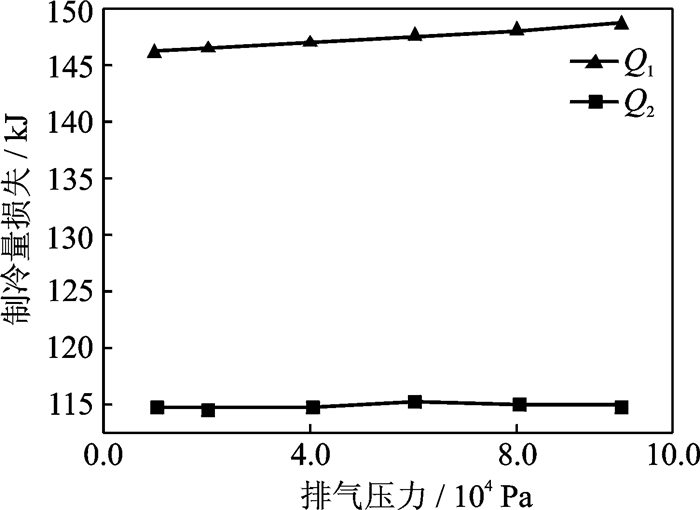
以排气压力1×105, 8×104, 6×104, 4×104, 2×104和1×104Pa为例,计算得到不同排气压力下两类制冷量损失,得到如图 6所示结果。
|
图 6 不同排气压力下的制冷量损失 Figure 6 Cooling capacity loss for varying conditions of exhaust pressure |
由图 6可知,随着排气压力的增大,第一类制冷量损失增加,这主要是由于排气压力增大使制冷剂的质量流量增加,制冷剂的温度下降过快,从而导致此类制冷量损失增加;第二类制冷量损失基本保持不变,说明排气压力对此类制冷量损失影响相对较小。因此,在实际设计过程中,应根据实际情况选择较小的排气压力。
5 结论针对传统的空冷方式存在的制冷量不足的问题,本文提出了一种能够满足飞艇全高度工作要求的制冷方案。根据以上研究,可以得出如下结论:
(1) 从对影响制冷量损失的因素的分析中可知,当其条件不变时,二氧化碳气瓶的储存温度较低、管道直径较大、排气压力较小时,制冷量损失相对较小。
(2) 从对两类制冷量损失的比较中看出,第一类制冷量损失基本都大于第二类制冷量损失。因此,在实际设计过程中要重点考虑减小第一类制冷量损失。
(3) 对于短时的上升过程,本文所提出的制冷方案能够解决传统空冷方式存在的制冷量不足的问题。
| [1] |
YAO Wei, LU Xiaochen, WANG Chao, et al.
A heat transient model for the thermal behavior prediction of stratospheric airships[J]. Applied Thermal Engineering, 2014, 70(1): 380–387.
DOI:10.1016/j.applthermaleng.2014.05.050
|
| [2] |
KHOURY G A, GILLETT J D. 飞艇技术[M]. 王生, 杨燕初, 马毅, 等, 译. 北京: 科学出版社, 2008: 19-25.
|
| [3] |
邓丽君. 一种临近空间浮空器热控系统的研究[D]. 南京: 南京理工大学, 2009.
DENG Lijun. Study on thermal control system of a near space vehicle[D]. Nanjing: Nanjing University of Scienee & Technology, 2009. |
| [4] |
DUMAS A, ANGELI D, TRANCOSSI M.
High altitude airship cabin sizing, pressurization and air conditioning[J]. Energy Procedia, 2014, 45: 977–986.
DOI:10.1016/j.egypro.2014.01.103
|
| [5] |
刘欣. 平流层飞行器设备舱热控制相关研究[D]. 北京: 北京工业大学, 2009.
LIU Xin. The relevant study of the thermal control of the equipment cabin of the stratospheric airship[D]. Beijing: Beijing University of Technology, 2009. |
| [6] |
李大鹏.
平流层飞艇通信系统载荷舱热控设计[J]. 低温与超导, 2011, 39(5): 78–80.
DOI:10.3969/j.issn.1001-7100.2011.05.018 LI Dapeng. Thermal control system design for stratospheric airship communication system gondola[J]. Cryogenics & Suprerconductivity, 2011, 39(5): 78–80. DOI:10.3969/j.issn.1001-7100.2011.05.018 |
| [7] |
王旭巍, 李兆杰, 才晶晶.
平流层飞艇设备舱的被动温控[J]. 计算机仿真, 2013, 30(8): 54–59.
DOI:10.3969/j.issn.1006-9348.2013.08.013 WANG Xuwei, LI Zhaojie, CAI Jingjing. Stratospheric airship equipment cabin's passive temperature control[J]. Compute Simulation, 2013, 30(8): 54–59. DOI:10.3969/j.issn.1006-9348.2013.08.013 |
| [8] |
周湘杰, 罗义平, 肖俊. 基于平流层飞艇的流体回路热控系统: 中国, CN202863755U[P]. 2013-04-10.
ZHOU Xiangjie, LUO Yiping, XIAO Jun. Thermal control system of fluid loops based on stratospheric airship: China, CN202863755U[P]. 2013-04-10. |
| [9] |
施红. 平流层飞艇并联式温度控制系统及控制方法: 中国, 201410247741X[P]. 2014-06-05.
SHI Hong. Temperature control system and methods in parallel of stratospheric airship: China, 201410247741X[P]. 2014-06-05. |
| [10] |
CAI Yufei, ZHU Chunling, JIANG Yanlong, et al.
Modeling and calculation of open carbon dioxide refrigeration system[J]. Energy Conversion and Management, 2015, 89: 92–98.
DOI:10.1016/j.enconman.2014.09.061
|
| [11] |
裴后举. 平流层飞艇电子设备舱的热设计研究[D]. 镇江: 江苏科技大学, 2015.
PEI Houju. Thermal design of the electronic equipment cabin of a stratospheric airship[D]. Zhenjiang: Jiangsu University of Science and Technology, 2015. |
| [12] |
徐雷. 救生舱环境控制系统的设计优化与实验研究[D]. 南京: 南京航空航天大学, 2015.
XU Lei. Optimal design and experiment research of the environment control system in a mine rescue cabin[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2015. |
| [13] |
蔡玉飞, 蒋彦龙, 周年勇, 等.
开放式二氧化碳制冷性能研究[J]. 南京航空航天大学学报, 2011, 43(4): 551–555.
DOI:10.3969/j.issn.1005-2615.2011.04.020 CAI Yufei, JIANG Yanlong, ZHOU Nianyong, et al. Performance of open carbon dioxide refrigeration[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(4): 551–555. DOI:10.3969/j.issn.1005-2615.2011.04.020 |
 2018, Vol. 50
2018, Vol. 50


