2. 中国航天科工集团北京动力机械研究所, 北京, 100074
2. Beijing Power Machinery Research Institute, China Aerospace Science and Engineering Group, Beijing, 100074, China
宽范围、高精准、高密度、高强度的快速战将是未来战争发展的重要趋势。涡轮基组合循环(Turbine based combined cycle, TBCC)发动机是涡轮发动机、亚燃/超燃冲压发动机组合的推进装置,能够实现变循环工作过程,使飞行器在不同的飞行条件(亚声速、超声速、高超声速)下都能得到良好的推进性能[1]。这些特点使得TBCC发动机成为高超声速飞行器和高超声速巡航导弹等未来航空武器的理想推进装置[2]。
目前,国外科研人员对航空发动机的推重比、油耗率、寿命等指标进行了大量的优化研究。自20世纪80年代以来,美国政府及工业部为提高发动机的性能制订了IHPTET计划,提出发动机推重比提高1倍,发动机生产和维护费用减少35%的目标[3-4]。后续提出的VAATE计划,进一步对发动机的性能提出更高要求,集中式控制算法不能满足高性能的需求,而分布式控制因为能够改善控制系统性能得以发展起来[5-7]。为此,美国研究人员对分布式控制系统进行了充分的理论论证并制定了非常详细的标准,对降低发动机重量、提高控制系统可靠性以及改善高温元器件性能进行了大量的研究[8]。其中,控制系统的拓扑结构对分布式控制系统控制性能至关重要。这是由于拓扑结构表示分布式控制系统中各个智能节点间的连接关系。若节点位置基本确定,节点间不同的线束连接形式将导致线束长短和节点间连通程度的不同。当线束密度一定时,线束长度一定程度上反映分布式控制系统重量。节点连通情况则反映了拓扑网络的可靠性。例如,所有智能节点全连通时,可靠性最高,即某一节点间连接故障时对网络正常工作影响最小,但是此时网络最为复杂,线束也最多。考虑两者间的冲突,研究者开展了大量的分布式控制系统拓扑结构优化研究,以期获得重量最轻、最可靠或者兼顾两者的最优拓扑结构。Kumar等人利用遗传算法针对具有单一拓扑类型的总线,优化了发动机分布式控制系统拓扑结构[9]。然而,分布式控制系统的一大优势在于其拓扑形式灵活性,即不局限于某一种拓扑结构。因此,在系统构成复杂、节点数量多时,单一类型拓扑结构对发动机重量和控制系统性能的提高有限。与之相比,混合型拓扑结构因高可靠性、良好扩展性和灵活性,成为分布式控制系统通讯网络拓扑结构的重要发展方向。国内在分布式控制系统的研究上起步比较晚,对拓扑结构的优化还处于起步阶段。
TBCC发动机工作状况复杂,控制回路多及其可调机构多,系统中包含大量的传感器、执行机构,传统集中式控制器在信号传输与处理上消耗大量资源,限制控制性能的提高。分布式控制在系统减重、可靠性提高和控制品质改善方面有着良好的优势,也带来系统总体拓扑构架设计方法的新问题。因此,国内外研究者针对总线形或星形系统拓扑结构开展优化研究,但不能满足TBCC发动机中控制系统众多约束条件下的拓扑结构需求。如考虑系统成本,TBCC中多个相邻传感器共享一个智能单元完成信号处理、采集与传输等功能;考虑智能可调机构的可靠性,其闭环控制系统将分布在执行现场附近,因此系统中不是所有元件都成为通信总线上的智能节点。这些TBCC分布式控制系统结构约束的满足需要考虑更为复杂混合型拓扑结构。
本文针对TBCC发动机分布式控制系统,以重量和可靠性为优化性能指标,运用粒子群算法和遗传算法开展其通讯网络环形和星形混合拓扑结构的优化研究,环形和星形混合拓扑结构示意图如图 1所示。分布式控制系统的重量主要是线束重量和所有控制器重量之和,控制器的质量与具体功能、工艺、材料等因素相关,难以估计,并且相比于线束重量而言控制器的重量较小。本文侧重于拓扑结构优化方法的探讨,因此暂时忽略控制器的质量,只考虑拓扑结构的线束重量和长度。可靠性的优化主要表现在通信冗余度以及控制器工作环境等方面的改善。
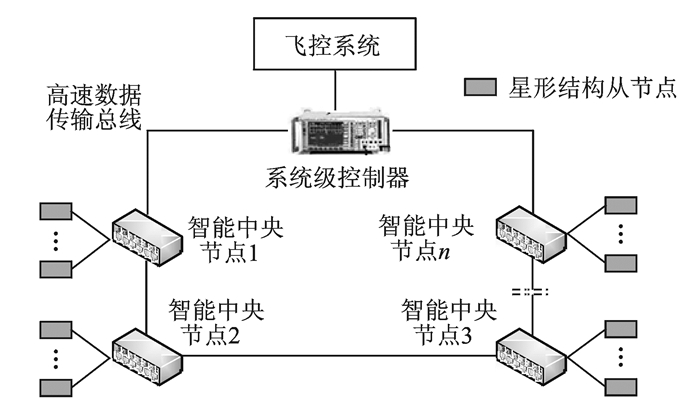
|
图 1 TBCC通信网络混合拓扑结构示意图 Figure 1 Mixed topology of TBCC communication network |
1 TBCC发动机布局方式和几何模型
目前TBCC主要有串联布局和并联布局两种布局方式。本文选取串联布局TBCC发动机作为研究对象,其结构如图 2所示。为了后续TBCC网络拓扑结构优化,将TBCC壳体简化为圆柱面。基于此建立TBCC圆柱体几何模型,如图 3所示,其中黑色部分为发动机高温区。
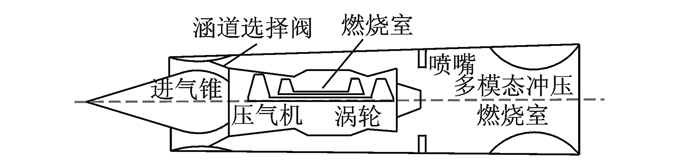
|
图 2 串联式TBCC结构示意图 Figure 2 Series TBCC structure |
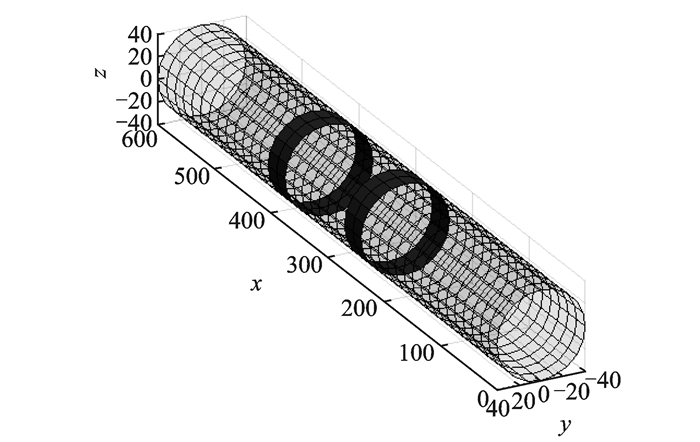
|
图 3 TBCC机匣三维坐标图 Figure 3 Three-dimensional coordinate diagram of TBCC casing |
假设图 2所示的TBCC发动机机匣为一长L、半径r的圆柱面。以发动机进气端截面圆圆心为坐标原点,发动机轴向方向为x轴,与x轴垂直的动机径向截面为y轴和z轴平面,建立空间三维坐标轴,如图 3所示。发动机机匣表面上点的坐标满足
| $ \left\{ {\begin{array}{*{20}{c}} {{y^2} + {z^2} = {r^2}}\\ {0 \le x \le L} \end{array}} \right. $ | (1) |
沿轴向每ΔL取一个截面圆,沿每个截面圆的周向位置将截面圆的表面划分为m等分的网格,每一个网格可以近似平面矩形,因此有N个等分的网格。采用自然数对所有网格点进行顺序编号,即1,2,…,N。定义邻接矩阵
| $ \mathit{\boldsymbol{M}}\left( {i,j} \right) = \left\{ {\begin{array}{*{20}{c}} {{d_{ij}}}&{网格\;i\;和\;j\;相邻}\\ 0&{其他} \end{array}} \right. $ | (2) |
式中dij为两个相邻节点i和j间的距离。
假设传感器、执行机构和分布式控制器都位于上述所建立的网格节点上,由此得到TBCC发动机的网络模型。基于该网格模型和邻接矩阵M,使用最短路径Floyed算法可以获得两个网格点之间的最短路径及其长度。网格模型有效的将空间复杂曲面上两点最短连线转化为空间最短连线的长度计算。
2 基于智能算法的TBCC混合拓扑结构优化TBCC发动机工况复杂,需要大量的传感器以及执行机构等发动机节点来实现发动机安全可靠的控制,并且传感器和执行机构的位置由TBCC发动机的结构布局决定。所以,发动机分布式控制通信网络的拓扑结构多样、优化难度大。本节基于智能优化算法对混合拓扑结构进行优化。首先,利用粒子群算法优化星形中央节点的位置以及每个星形中央节点连接的发动机节点;然后,利用遗传算法对中央节点之间的环形总线结构进行优化;最后,由星形结构以及环形总线结构优化结果得到混合拓扑结构。TBCC混合拓扑结构优化流程如图 4所示。
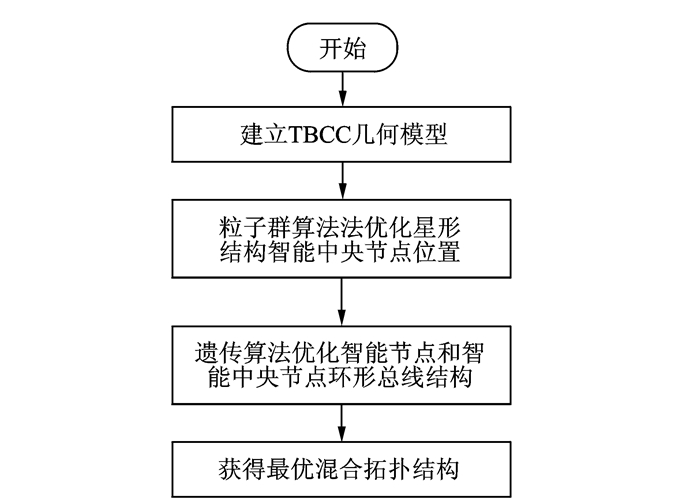
|
图 4 TBCC混合拓扑结构优化流程 Figure 4 TBCC hybrid topology optimization process |
2.1 基于粒子群算法的星形结构中央节点位置优化
粒子群算法(Particle swarm algorithm, PSO)是基于鸟群觅食开发的一种进化算法,从随机解出发,利用全局搜索和局部搜索来找到最优解。由于这种优化方式,PSO在解决最优点坐标问题时拥有较高的效率和精度。
针对图 1中n个智能中央节点,其粒子群算法中位置和速度编码分别为
| $ \mathit{\boldsymbol{x}} = \left[ {{z_1},{\theta _1}, \cdots ,{z_n},{\theta _n}} \right] $ | (3) |
| $ \mathit{\boldsymbol{\dot v}} = \left[ {{{\dot z}_1},{{\dot \theta }_1}, \cdots ,{{\dot z}_n},{{\dot \theta }_n}} \right] $ | (4) |
式中:zi表示粒子的轴向位置;θi表示粒子的周向位置。由于TBCC机匣为圆柱面,且各节点都位于机匣表面,所以半径不需要优化。
粒子群算法本质上是使用差分方程(5)来更新粒子当前位置量,速度则是利用已发现的全局以及局部最优解的信息(6)来更新,即
| $ {\mathit{\boldsymbol{x}}_{i,j}} = {x_{i,j - 1}} + {v_{i,j}} $ | (5) |
| $ {\mathit{\boldsymbol{v}}_{i,j}} = w{v_{i,j - 1}} + {\varphi _p}{r_p}\left( {{p_{i,j}} - {\mathit{\boldsymbol{x}}_{i,j}}} \right) + {\varphi _g}{r_g}\left( {g - {\mathit{\boldsymbol{x}}_{i,j}}} \right) $ | (6) |
式中:w为保持上一次迭代速度量的惯性权重; φp和φg分别为局部搜索和全局搜索跟踪最优解的权重系数;rp和rg为[0, 1]区间内的随机数。
为了更快更准确地得到最优解,需要对上述3个权重系数进行合理设置。当粒子靠近最优解时,等式(5)右边后两项的值趋于0,所以对φp和φg均取为定值2。对惯性权重的取值的目的是当粒子靠近最优解时,w值趋向于0以保证解得精度,当粒子远离最优解时,w值稍大些可以使粒子更快的靠近最优解。w的取值采用非线性权值递减策略[10],即
| $ \begin{array}{*{20}{c}} {w = \left( {{W_{\max }} - {W_{\min }}} \right){{\left( {\frac{{{N_{\rm{C}}}}}{{{N_{\rm{L}}}}}} \right)}^2} - }\\ {2\left( {{W_{\max }} - {W_{\min }}} \right)\frac{{{N_{\rm{C}}}}}{{{N_{\rm{L}}}}} + {W_{\max }}} \end{array} $ | (7) |
式中:Wmax为最大的惯性权重,即初代粒子种群惯性权重w的值,相应的Wmin为最小的惯性权重,即末代粒子种群惯性权重w的值;NC表示当前种群迭代次数;NL表示粒子群算法所需迭代的总次数。
选取适应度函数来评价智能中央节点位置粒子的优劣
| $ f = \sum\limits_{k = 1}^n {\left( {\min \left( {{d_k}} \right)} \right)} + {p_{\rm{s}}} $ | (8) |
式中:n为图 1中星型结构从节点的个数; dk为从节点到各个智能中央节点的距离集合,ps是温度惩罚函数; min()表示每个从节点到各个智能中央节点的距离集合中最小值,即每个发动机节点(从节点)都连接到距离最近的智能中央节点组成星型结构。利用基于网格模型的最短路径Floyed算法可计算得到dk。考虑智能节点中电子设备高温环境下易发生故障,所以式(8)中加入ps使得待优化位置粒子远离高温区。需要注意的是适应度函数(8)仅以线束长度和可靠性作为评价标准,若要对其他条件进行限制,可在适应度函数上加上相应惩罚函数。
利用粒子群算法对智能中央节点的位置进行优化的同时,也将所有的发动机节点按照距离进行分类,每个发动机节点与距离最近的智能中央节点相连接组成多个星形结构。粒子群算法以星形结构的线束总长度为优化目标,同时优化中央节点位置以及从节点分类来获取星形结构的最短线束长度。
2.2 基于遗传算法的智能中央节点环形拓扑结构优化智能中央节点环形拓扑结构优化是对中央节点之间的连接方式的优化,保证每两个中央节点都有两条完全独立的通信通道的同时使得所需的线束长度最短。中央节点之间的连接方式采用环形总线拓扑结构,本小节中将构建由智能中央节点和传输线路组成的TBCC分布式控制系统通信总线抽象图,通过抽象图的顶点和边的关系反映该通信总线中各智能中央节点的关系,进而利用遗传算法优化环形总线拓扑结构[11]。
设抽象图G=(V, E)为TBCC分布式控制系统通信总线,其中假设发动机中n个总线节点的集合为
| $ V = \left\{ {{V_1},{V_2},{V_3}, \cdots ,{V_n}} \right\} $ | (9) |
式中Vi(i=1, 2, …, n)表示网络中各节点。相应地,抽象图中边的集合为
| $ \begin{array}{*{20}{c}} {E = \left\{ {\left( {{V_1},{V_2}} \right),\left( {{V_1},{V_3}} \right), \cdots ,\left( {{V_1},{V_n}} \right), \cdots ,} \right.}\\ {\left. {\left( {{V_n},{V_1}} \right), \cdots ,\left( {{V_n},{V_{n - 1}}} \right),\left( {{V_n},{V_n}} \right)} \right\}} \end{array} $ | (10) |
式中(Vi, Vj)表示节点Vi和Vj构成的边。为了描述抽象图G中节点与节点的邻接关系,定义抽象图邻接矩阵
| $ \mathit{\boldsymbol{X}} = {\left[ {x\left( {{V_i},{V_j}} \right)} \right]_{n \times n}} $ | (11) |
式中
| $ \begin{array}{*{20}{c}} {x\left( {{V_i},{V_j}} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1\\ 0 \end{array}&\begin{array}{l} 节点\;{V_i}\;与节点\;{V_j}\;邻接\\ 节点\;{V_i}\;与节点\;{V_j}\;不邻接 \end{array} \end{array}} \right.}\\ {i \ne j;i,j = 1,2, \cdots ,n}\\ {x\left( {{V_i},{V_j}} \right) = 0\;\;\;\;i = j;i,j = 1,2, \cdots ,n} \end{array} $ | (12) |
进一步描述智能中央节点间的连接关系和距离信息,定义加权矩阵
| $ \mathit{\boldsymbol{D}} = {\mathit{\boldsymbol{D}}^{\rm{T}}} = {\left[ {d\left( {{V_i},{V_j}} \right)} \right]_{n \times n}} $ | (13) |
形成能够表示线路长度的加权图。
(1) 个体的选取及编码
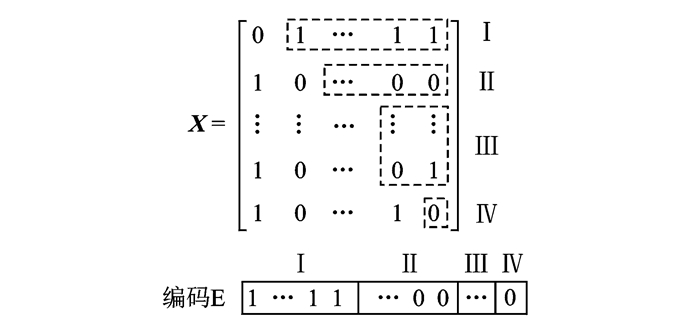
由于邻接矩阵X为对称阵,且x(Vi, Vi)=0, i=1, …, n,所以个体p的选择为
| $ \begin{array}{l} p = \left\{ {x\left( {{V_1},{V_2}} \right),x\left( {{V_1},{V_3}} \right), \cdots ,x\left( {{V_1},{V_n}} \right),} \right.\\ \;\;\;\;\left. {x\left( {{V_2},{V_3}} \right), \cdots ,x\left( {{V_2},{V_n}} \right), \cdots ,x\left( {{V_{n - 1}},{V_n}} \right)} \right\} \end{array} $ | (14) |
个体编码方式如图 5所示,这种设计表明每个个体都是TBCC分布式控制系统通信环形总线的一种可能拓扑结构。个体中每个基因x(Vi, Vj)代表相应地邻接关系,所以个体不再需要编码,只需随机产生只有0和1的一组序列。
|
图 5 总线拓扑结构编码方式 Figure 5 Bus topology coding |
(2) 目标函数和适应度
优化目标函数选为线束总长度L,且
| $ L = \frac{1}{2}\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {x\left( {{V_i},{V_j}} \right)d\left( {{V_i},{V_j}} \right)} } $ | (15) |
考虑拓扑结构中节点间连接的可靠性,对目标进行一定的约束,约束条件为任意的两个节点之间存在两条独立路径(即两条路径没有相交的部分),若不满足约束条件,对个体施以惩罚pg
| $ {p_g} = {10^3}L $ | (16) |
因此,个体的适应度设为
| $ F = L + {p_g} $ | (17) |
将种群中每个个体进行解码并代入目标函数中进行计算,并判断是否满足约束条件,根据判断的结果计算个体的适应度值。
(3) 选择操作
按个体适应度值与所有个体适应度值总和的比值大小决定其子孙遗留的可能性。若某个体i(某个通信网络拓扑结构)其适应度为fi,则其被选取的概率表示为
| $ {p_i} = \frac{{{f_i}}}{{\sum\limits_{i = 1}^{100} {{f_i}} }} $ | (18) |
(4) 交叉与变异
考虑到算法的计算速度和收敛程度,选择交叉概率为0.8,变异概率为0.3进行染色体交叉、变异。
(5) 优化流程
重复步骤(1)—(5)直至遗传算法的适应度函数收敛。
2.3 基于智能算法的混合拓扑结构优化相比于单一拓扑结构,混合拓扑结构具有高可靠性、易于扩展、易于维护和速度较快等优点,满足分布式控制系统对通信网络性能和结构的需求[12-13]。本节针对TBCC发动机分布式控制系统,以重量和可靠性为优化性能指标,给出通信网络线束质量的计算公式,并结合2.1节以及2.2节中优化方法对混合结构进行优化。
如图 1所示,TBCC通信网络混合拓扑结构是由环形结构和星形结构混合而成。其线束质量主要分为2个部分,即智能中央节点间环形结构线束质量和所有星形结构线束质量。将拓扑结构的可靠性指标作为惩罚函数加入智能算法优化过程中,如式(8)所示,以避免智能中央节点出现在高温区。当智能节点远离高温区,对智能节点散热设计等可以简化,智能节点的质量可以大幅降低[14]。考虑到每个智能节点的质量涉及到具体功能、工艺、材料等,需要逐一评估,而本文侧重于拓扑结构优化方法的探讨,因此暂时忽略智能节点的质量[15-16]。
环形和星形混合拓扑结构优化过程分为4个步骤:
(1) 确定选取智能中央节点的个数;
(2) 利用粒子群算法优化智能中央节点位置以及混合拓扑结构中星形结构的从节点分类信息;
(3) 利用遗传算法优化智能中央节点之间的环形拓扑结构;
(4) 根据最短星形结构线束长度以及最短环形结构线束长度,确定优化后混合结构总共需要的线束长度。
混合拓扑结构所需线束长度Ld为
| $ {L_{\rm{d}}} = {L_z} + {L_x} $ | (19) |
式中:Lz为环形结构线束长度; Lx为星形结构线束长度。由2.1节可以优化得到最优的星形结构以及最优智能中央节点位置,计算每个星形结构所需的线束长度之和得到Lx。由2.2节可以得到最优的环形总线结构,计算环形总线结构所需线束长度得到Ld。
3 仿真实例 3.1 TBCC几何尺寸以及通信节点以某TBCC发动机分布式控制系统为研究对象,其壳体简化为长6 m,半径0.4 m的圆柱体,三维立体图如图 3所示。
选取其具有代表性的传感器、执行机构和控制器开展通信总线拓扑结构优化研究,节点信息如表 1所示。
| 表 1 TBCC发动机节点信息 Table 1 Nodes' information of the TBCC engine |
3.2 基于粒子群算法的星形结构中央节点位置优化仿真
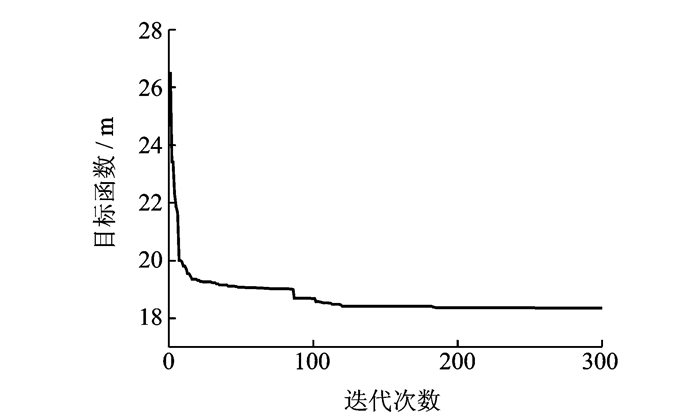
串联式TBCC发动机存在两个高温区,分别为涡轮燃烧室和冲压燃烧室所在的区域。由两个高温区将发动机机匣分为3个区域,如图 3所示,黑色为高温区。考虑到星形中央节点的质量以及发动机结构,选取6个星形中央节点连接发动机节点,形成6个星形结构。式(6)中φp和φg均取为定值2。式(7)中Wmin取值为0.2,Wmax取值为2,粒子群算法所需迭代的总次数NL为300。当6个节点中有j个节点的位置在高温区内,式(8)中惩罚函数ps=5×j。
利用粒子群算法对智能节点位置优化迭代过程如图 6所示,优化得到各智能中央节点的位置如表 2所示,各智能中央节点所连接的从节点如表 3所示。
|
图 6 粒子群优化迭代过程 Figure 6 Particle swarm optimization iterative process |
| 表 2 智能中央节点 Table 2 Information of smart central Node |
| 表 3 智能中央节点优化后的信息 Table 3 Information after optimization of smart central Node |
3.3 基于遗传算法的智能中央节点环形拓扑结构优化仿真
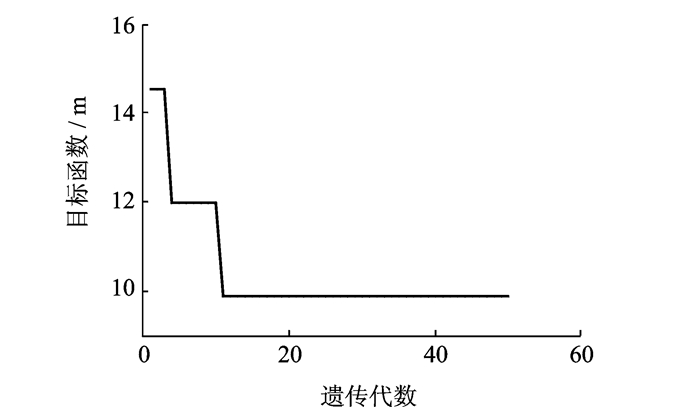
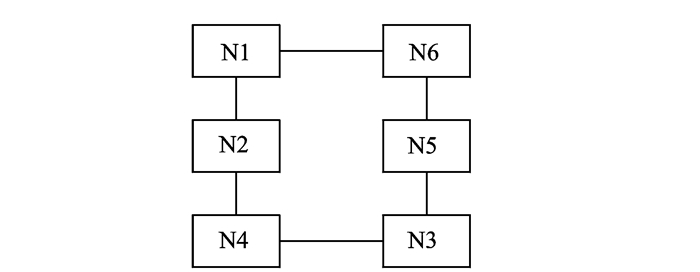
由3.2节可以得到利用粒子群算法优化的智能中央节点的位置,在星形结构最优的基础上利用遗传算法对智能中央节点环形拓扑结构进行优化,考虑到计算时间和收敛程度,取种群中个体数目为100,遗传代数为50。优化过程如图 7所示,优化得到的环形总线连接方式如图 8所示。
|
图 7 遗传算法优化过程目标函数曲线 Figure 7 Objective function curve in optimization process of GA |
|
图 8 优化后智能中央节点环形拓扑结构 Figure 8 Optimized ring topology of smart central node |
3.4 智能算法优化得到混合拓扑结构
在环形总线拓扑结构中,系统级控制器控制着总线上的其他节点的工作方式并且与飞控系统进行通信[17]。但是对于系统级控制器位置并没有限制,不妨将系统级控制器放置在智能中央节点1的位置,减少线束长度。由上述步骤所述,利用粒子群算法和遗传算法优化得到的混合拓扑结构三维图如图 9所示。
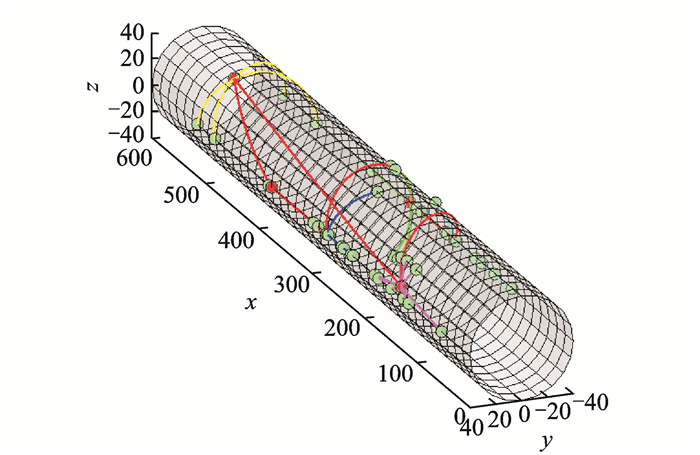
|
图 9 TBCC优化后混合拓扑结构立体图 Figure 9 TBCC optimized mixed topology stereogram |
图 9中绿点表示发动机节点,红点表示智能中央节点,红线表示环形总线,紫线、青线、蓝线、绿线、黑线,黄线分别表示智能中央节点1, 2, 3, 4, 5和6所在的星形结构的连线。
如式(19)所示,混合拓扑结构所需线束的长度为6个星形结构线束长度以及环形总线线束长度之和,由上述优化结果可以得到线束总长Ld为28.3 m。
以集中式控制系统通信网络拓扑结构为基线,对比混合式结构与集中式结构的线束重量,分析混合式的结构在重量以及可靠性上的优势。目前,集中式控制系统通信网络拓扑结构采用的是星形结构,本文采用遍历法优化集中式控制的星形结构,具体方法为遍历发动机网格模型中的每个网格得到最优的星形结构中央控制器位置,计算得到星形结构所需的线束长度。利用遍历法获得集中式控制系统星形结构的拓扑结构的最优中央节点编号为25 724,轴向257 cm,周向86°,所需线束总长Lc为58.8 m。
发动机控制系统的重量Ws为控制器重量We与线束重量Wl之和。在线束一致的前提下线束长度与重量成正比,设线束单位长度的重量为ρl,其关系如下述公式所示
| $ {W_{\rm{s}}} = {W_{\rm{e}}} + {W_{\rm{l}}} $ | (20) |
| $ {W_{\rm{l}}} = {\rho _{\rm{l}}}{L_{\rm{p}}} $ | (21) |
式中Lp为线束长度。定义线束减重比为
| $ \delta = \frac{{{W_{\rm{c}}} - {W_{\rm{d}}}}}{{{W_{\rm{c}}}}} \times 100\% $ | (22) |
式中,Wd和Wc分别为分布式和集中式拓扑结构下控制系统的重量。在线束一致的前提下线束长度与线束重量成正比,忽略节点控制器的重量,线束减重比可以表示为
| $ \delta = \frac{{{L_{\rm{c}}} - {L_{\rm{d}}}}}{{{L_{\rm{c}}}}} \times 100\% $ | (23) |
通过仿真计算得到混合拓扑结构下的分布式控制系统线束重量比星形拓扑结构的集中式控制系统降低了51.9%。需要指出的是,上述减重比是仅在线束长度(重量)意义下分析结果,实际分布式控制系统的重量还需要考虑线束接口、智能节点等重量的变化。
对混合拓扑结构的可靠性优化主要体现在环形总线拓扑结构独立双通道通信以及对智能节点位置优化时避免出现在高温区[18]。当总线一点发生故障时,总线上两点直接的通信可以避开故障点进行正常通信,同时远离高温区可以降低节点工作时故障率,提高通信网络的可靠性。
4 结束语本文开展了TBCC发动机分布式控制系统通信网络拓扑结构优化研究。提出星形-环形混合拓扑结构的TBCC分布式控制系统网络拓扑结构。考虑高温区限制和独立通信通路数的网络可靠性要求,基于粒子群算法和遗传算法优化获得线束长度最短意义下的重量最小混合型拓扑结构。仿真实例表明,具有混合型拓扑结构的分布式控制系统比集中式控制系统相比,线束重量降低了51.9%。
| [1] |
王占学, 刘增文, 王鸣, 等.
涡轮基组合循环发动机技术发展趋势和应用前景[J]. 航空发动机, 2013, 39(3): 12–17.
DOI:10.3969/j.issn.1672-3147.2013.03.003 WANG Zhanxue, LIU Zengwen, WANG Ming, et al. Future development and application of turbine based combined cycle engine[J]. Aeroengine, 2013, 39(3): 12–17. DOI:10.3969/j.issn.1672-3147.2013.03.003 |
| [2] |
李文杰, 叶蕾.
美国航空航天局涡轮基组合循环发动机技术发展研究[J]. 战术导弹技术, 2015(3): 1–6.
LI Wenjie, YE Lei. TBCC technology development of NASA[J]. Tactical Missile Technology, 2015(3): 1–6. |
| [3] |
VIARS P. The impact of IHPTET on the engine/aircraft system[C]//Aircraft Design and Operations Meeting. Seattle, USA: AIAA, 1988: 2137-1-8. |
| [4] |
SWEETMAN B.
IHPTET (Integrated high-performance turbine engine technology) spawns engines for 21st century[J]. Interavia, 1989, 44(11): 1113–1115.
|
| [5] |
梁春华.
通用的经济可承受的先进涡轮发动机研究计划的主要特点[J]. 航空发动机, 2011, 37(5): 58–62.
DOI:10.3969/j.issn.1672-3147.2011.05.016 LIANG Chunhua. Key features of versatile affordable advanced turbine engine program[J]. Aeroengine, 2011, 37(5): 58–62. DOI:10.3969/j.issn.1672-3147.2011.05.016 |
| [6] |
MAKOWITZ R, TEMPLE C. Flex ray-A communication network for automotive control systems[C]//IEEE International Workshop on Factory Communication Systems, 2006 IEEE International Workshop on factory Communication Systems. Torino, Italy: IEEE, 2006: 207-212. |
| [7] |
BARTOLOTTA P A, MCNELIS N B, SHAFER D G. High speed turbines: Development of a turbine accelerator (RTA) for space access[C]//12th AIAA International Space Planes and Hypersonic Systems and Technologies. Norfolk, USA: AIAA, 2003: 6943-1-6. |
| [8] |
THOMPSON H A, CHIPPERFIELD A J, FLEMING P J, et al.
Distributed aero-engine control systems architecture selection using multi-objective optimisation[J]. Control Engineering Practice, 1999, 7(5): 655–664.
DOI:10.1016/S0967-0661(99)00011-8
|
| [9] |
KUMAR A, PATHAK R M, GUPTA Y P, et al.
A genetic algorithm for distributed system topology design[J]. Computers & Industrial Engineering, 1995, 28(3): 659–670.
|
| [10] |
陈贵敏, 贾建援, 韩琪.
粒子群优化算法的惯性权值递减策略研究[J]. 西安交通大学学报, 2006, 40(1): 53–61.
DOI:10.3321/j.issn:0253-987X.2006.01.013 CHEN Guimin, JIA Jianyuan, HAN Qi. Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm[J]. Journal of Xi'an Jiaotong University, 2006, 40(1): 53–61. DOI:10.3321/j.issn:0253-987X.2006.01.013 |
| [11] |
宋军强, 汤丽丽, 潘慕绚, 等.
航空发动机分布式控制拓扑结构优化方法[J]. 航空动力学报, 2016, 31(6): 1435–1440.
SONG Junqiang, TANG Lili, PAN Muxuan, et al. Aero-engine distributed control system topology optimization method[J]. Journal of Aerospace Power, 2016, 31(6): 1435–1440. |
| [12] |
宋军强, 潘慕绚, 黄金泉.
航空发动机分布式控制系统技术分析及系统方案[J]. 航空动力学报, 2013, 28(10): 2391–2400.
SONG Junqiang, PAN Muxuan, HUANG Jinquan. Technology analysis and system scheme for aero-engine distributed control system[J]. Journal of Aerospace Power, 2013, 28(10): 2391–2400. |
| [13] |
关越, 潘慕绚.
基于DSP的航空发动机分布式控制TTCAN总线的节点设计[J]. 航空发动机, 2013, 39(4): 61–66.
DOI:10.3969/j.issn.1672-3147.2013.04.012 GUAN Yue, PAN Muxuan. Design of TTCAN node for aeroengine distributed control system based on DSP[J]. Aeroengine, 2013, 39(4): 61–66. DOI:10.3969/j.issn.1672-3147.2013.04.012 |
| [14] |
NEUDECK P G, OKOJIE R S, CHEN L Y.
High-temperature electronics-a role for wide bandgap semiconductors[J]. Proceedings of the IEEE, 2002, 90(6): 1065–1076.
DOI:10.1109/JPROC.2002.1021571
|
| [15] |
LEE K C, MAN H K, LEE S, et al.
IEEE-1451-based smart module for in-vehicle networking systems of intelligent vehicles[J]. IEEE Transactions on Industrial Electronics, 2004, 51(6): 1150–1158.
DOI:10.1109/TIE.2004.837879
|
| [16] |
JACKSON B. A stochastic optimization tool for determining spacecraft avionics box placement[C]//Aerospace Conference Proceedings. Bigsky, USA: IEEE, 2002: 2373-2382. |
| [17] |
CULLEY D E, BEHBAHANI A. Communication needs assessment for distributed turbine engine control: NASA, Technical Manual TM-2008-215419[R]. Cleveland, Ohio: Glenn Research Center, 2008. |
| [18] |
DUNBAR L. Turbine configuration impact on advanced IHPTET engine system mission capabilities[C]//26th Joint Propulsion Conference. Orlando, USA: AIAA, 1990: 2739-1-15. |
 2018, Vol. 50
2018, Vol. 50


