热电制冷,又称温差电制冷或半导体制冷,是基于帕尔贴效应的一种主动制冷方式,在航空航天、军事、医疗和日常生活等方面具有重要的应用价值和广阔的发展前景。尤其在航空航天领域,热电制冷器与飞行器在功能、结构方面的一体化设计是目前应用的重点方向。通常喷气式战斗机的无线电设备即采用热电制冷[1]。GE公司曾研发出利用半导体制冷温控的等电聚焦电泳仪,电泳温度在15~25 ℃范围[2]。近年来,热电制冷在航空航天领域逐渐显现出向微小型化发展的趋势[1]。美国航空航天局和国家喷气动力实验室利用微电子机械系统开发了用于航天电子冷却的高性能微型半导体制冷器,散热面积仅有0.55 mm2[3]。热电制冷的优点是无需制冷剂,清洁无污染,无需外界机械动力、无噪声、无振动,可通过改变电流大小调整制冷量和冷却速度,结构紧凑、体积小、质量轻、寿命长,这对于航空航天有着至关重要的意义。热电制冷的缺点也很明显,材料成本高,制冷效率偏低。
多年来,国内外学者从不同角度针对热电制冷进行了一系列的深入研究。Mccarty[4]提出了变物性参数条件下热电制冷器的一维数值模型,并将所得结果与常物性参数条件进行对比,发现变物性参数条件下最大温差ΔTmax提高3 ℃以上,而冷端温度降低8 ℃以上。申利梅等[5]分析了两组热电模块在不同热连接与电连接方式下的制冷性能,着重探讨了工作电流、热电偶对数比和面长比对4种连接方式的制冷量和制冷系数的影响,最终获得了不同连接方式下的最佳工况和适用范围。杨凡超等[6]针对热电偶中非均匀焦耳热建立了数值模型,在常微分线性方程的基础上,使用分流和叠加的方法,提出了一种求解热电偶内温度和热流量分布的工程计算方法,并最终推导出第二类边界条件下热电偶中温度和热流量分布的计算公式。Chang等[7]基于有限体积法和点逐次超松弛算法设计了一套计算程序,用以预估热电设备中的塞贝克、帕尔贴效应以及焦耳热,为热电设备的性能优化提供理论指导。文献[8]遵循热设计原理,在冷端与热源之间增加了缓冲板,建立了新的电子设备微型热电制冷器分析模型,更有利于提高电子冷却性能。
国内外大部分研究均针对常规垂直结构的热电元件,很少涉及外形结构对制冷性能影响的研究,因此本文提出了倾斜结构形式的热电元件,并且以常规的垂直型结构作参考,从热电制冷的基本原理出发,基于ANSYS Workbench分别对不同种热电元件进行多物理场耦合分析,得到热电元件的温度场和电场分布,研究探讨了倾斜角度和制冷性能之间的关系,阐明倾斜结构的特点与优势,寻找出新的技术方案,为微小型、小功耗热电制冷设备的功能优化提供了有效的思路和借鉴。
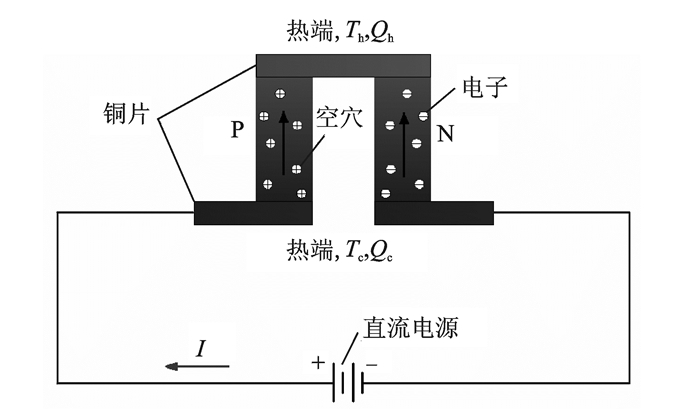
1 热电元件分析模型 1.1 基本原理热电制冷原理如图 1所示。当热电元件接通电源后,电流先后通过P形半导体和N形半导体,由于空穴和电子的迁移作用,在半导体和铜片的接触面处产生热效应,一端制热,温度升高,另一端制冷,温度降低,最终形成温度梯度。因此,可以认为,热电制冷的本质是电场和温度场的一种耦合效应[9]。
|
图 1 热电制冷原理图 Figure 1 Scheme of thermoelectric cooling |
1.2 几何模型
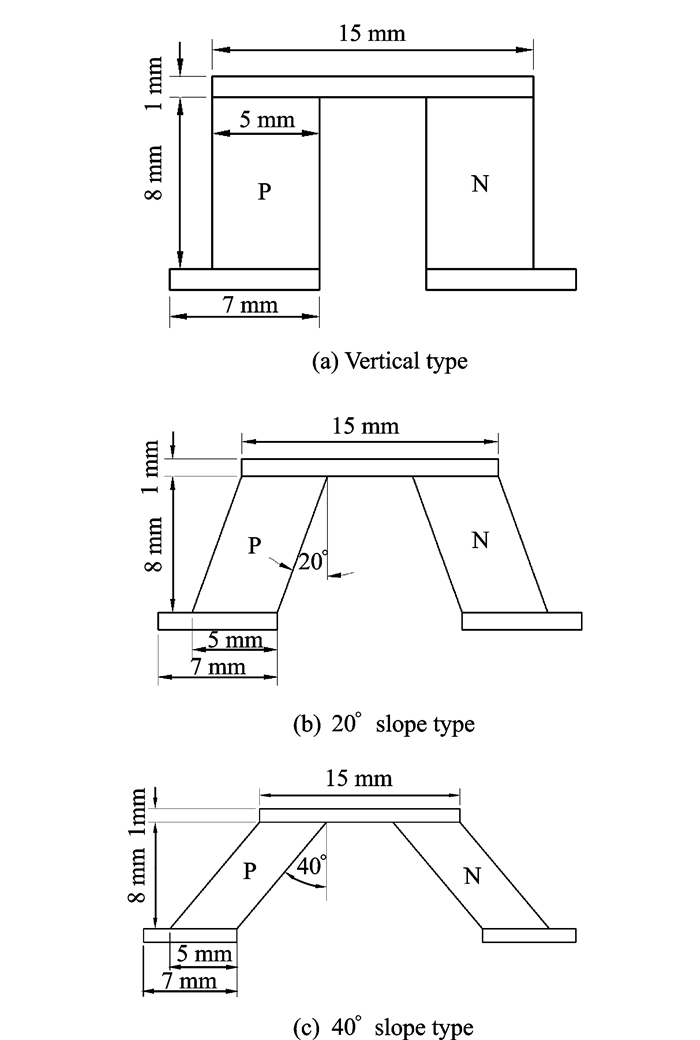
本文首先研究3种不同倾斜角度的热电元件,如图 2所示。
|
图 2 热电元件几何模型 Figure 2 Geometric model of thermoelectric element |
3种结构垂直于纸面的厚度均为5 mm。图 2(a)垂直形即为常规热电元件,同时作为其他两种类型的参考结构。图 2(b)为20°倾斜形,P, N形半导体设计成平行六面体结构,倾斜角度为20°,但横截面积和垂直高度不变。图 2(c)为40°倾斜形,P, N形半导体均设计成平行六面体结构,倾斜角度为40°,同时横截面积和垂直高度不变。3种热电元件倾斜角度不同,但不管是P形半导体还是N形半导体,体积均不发生变化,即3种结构形式的半导体材料用量相同,因此3种结构具有逻辑上的可比性。
1.3 物理模型为了问题的简化和计算的方便,本文提出以下假设:(1)热电元件在稳态条件下运行;(2)在热电制冷过程中,汤姆森效应是1种二级效应,因而可将其忽略不计[10];(3)不考虑冷、热端与铜片的接触热阻[11];(4)热电元件侧面绝热,与外界无热交换[12];(5)将热电材料视为常物性。因为本文着重研究3种结构热电元件的制冷性能对比,所以常物性并不影响热电元件性能的相对优劣。材料的物性参数参考文献[13],取T=303 K时的值,如表 1所示。
| 表 1 材料物性参数 Table 1 Physical property parameters of materials |
1.4 控制方程
在热电制冷过程[14]中,热通量三维控制方程可表述为
| $ \nabla \cdot \mathit{\boldsymbol{q}}\text{=}\dot{q} $ | (1) |
式中:q为热通量矢量(W/m2);
| $ \mathit{\boldsymbol{q}}\text{=}\alpha T\mathit{\boldsymbol{j}}\text{-}k\nabla T $ | (2) |
式中:α代表塞贝克系数(V/K);k表示热导率(W/(m·K))。将式(2)代入式(1),可得
| $ \dot{q}=-k{{\nabla }^{2}}T+T\mathit{\boldsymbol{j}}\cdot \nabla \alpha +\alpha \mathit{\boldsymbol{j}}\cdot \nabla T+\alpha T\left( \nabla \cdot \mathit{\boldsymbol{j}} \right) $ | (3) |
由于常物性,所以▽α=0;因为稳态,故而▽· j =0,最终,式(3)式化简为
| $ \dot{q}=-k{{\nabla }^{2}}T+\alpha \mathit{\boldsymbol{j}}\cdot \nabla T $ | (4) |
而体生成热
| $ \dot{q}=\mathit{\boldsymbol{j}}\cdot \mathit{\boldsymbol{E}} $ | (5) |
其中E为电场强度(V/m),可表述为
| $ \mathit{\boldsymbol{E=}}\rho \mathit{\boldsymbol{j+}}\alpha \nabla T $ | (6) |
式中:ρ代表电阻率,Ω·m;综合式(4—6),可得
| $ \rho \left( \mathit{\boldsymbol{j}}\cdot \mathit{\boldsymbol{j}} \right)+k{{\nabla }^{2}}T=0 $ | (7) |
本文借助ANSYS Workbench中的Mesh功能对3种模型划分结构化网格,然后进行网格独立性检验。设定不同的最小网格尺寸,分别为1, 0.5, 0.2 mm, 设定电流值为1 A,热端温度为37 ℃,其余边界条件保持默认。表 2是不同最小网格尺寸所对应的冷端温度和相对偏差,表 3, 4分别给出了20°和40°倾斜形网格的独立性检验。
| 表 2 垂直形网格独立性检验 Table 2 Grid independence test for vertical type |
| 表 3 20°倾斜形网格独立性检验 Table 3 Grid independence test for 20° slope type |
| 表 4 40°倾斜形网格独立性检验 Table 4 Grid independence test for 40° slope type |
这里以最小网格尺寸0.2 mm为参考值,当最小网格尺寸为1 mm时,3种模型中最大相对偏差为0.014%;当最小网格尺寸为0.5 mm时,3种模型中最大相对偏差为0.005%。由于相对偏差均小于1%,所以为了计算的快捷,3种模型网格划分均可设定最小网格尺寸为1 mm。
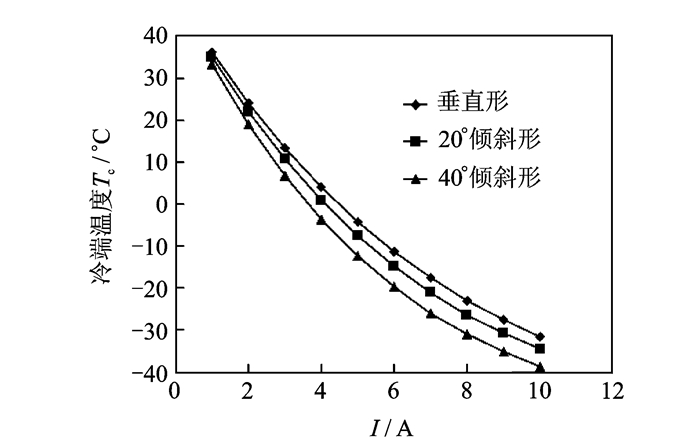
3 多物理场耦合分析 3.1 冷端温度与电流的关系假定3种热电元件的热端温度均为50 ℃,并通以相等的电流,进而分析对比热电元件冷端温度的相对大小。仿真结果如图 3所示。
|
图 3 冷端温度随电流的变化关系 Figure 3 Cold side temperature versus current |
冷端温度均随电流的增大而降低,但温度降低的速率越来越小,即温度下降越缓慢。冷端温度由高至低依次是垂直形、20°倾斜形、40°倾斜形。所以,就获取更低的制冷温度而言,40°倾斜形性能最佳,20°倾斜形其次,垂直形最差。从而可以得到结论:倾斜角度越大,制冷温度越低。从图 3中还可发现,随着电流的增大,不同热电元件冷端温度的差值先增大后减小。例如,当I=1 A时,相比于垂直形,20°倾斜形拥有1.157 ℃的差值,而40°倾斜形则对应有2.937 ℃的差值;当I=5 A时,同样相比于垂直形,两项差值分别是3.357和8.133 ℃;当I=10 A时,两项差值又分别是2.877和7.099 ℃。
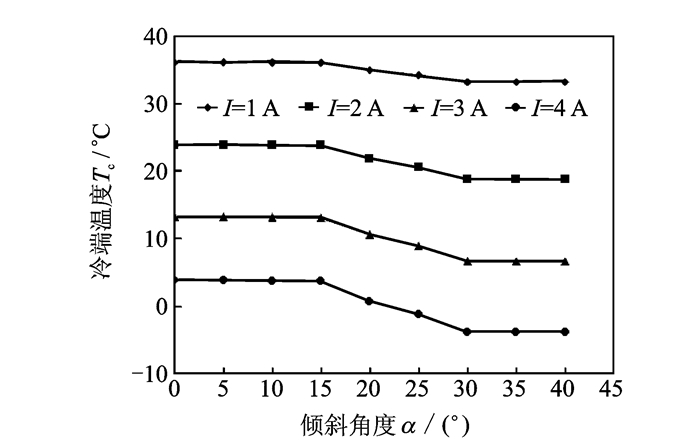
为了进一步验证倾斜角度对热电元件制冷性能的影响,本文又分析了不同功率条件下的多种倾斜角度,涵盖范围是0°~40°,电流值介于1~4 A,如图 4所示。
|
图 4 冷端温度随倾斜角度的变化关系 Figure 4 Cold side temperature versus slope |
就总体趋势而言,倾斜角度越大,制冷温度越低,从而印证上文结论。当倾斜角度α在0°~15°和30°~40°范围内变化时,冷端温度变化并不显著,近似为水平直线;当α处于15°~30°范围内,冷端温度有明显的梯度。因此,15°~30°倾角范围对于改善热电元件制冷性能影响较大,具有重要的研究意义。
3.2 制冷量与电流、温差的关系探讨3种不同热电元件的制冷量Qc随电流I和温差ΔT的变化关系,同时进行分析对比。
控制冷热端温差一定,改变电流大小,得到3种不同热电元件的制冷量随电流的变化关系。以ΔT=20 ℃为例,结果如图 5所示。
|
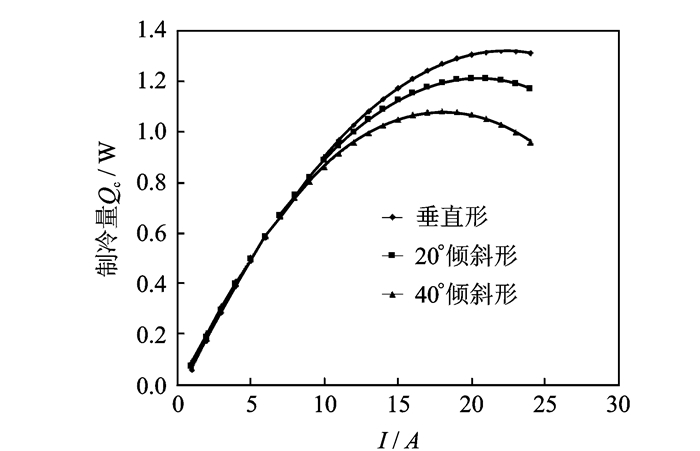
图 5 制冷量随电流的变化关系 Figure 5 Cooling capacity versus current |
随着电流的增大,制冷量先增大后减小,所以每条变化曲线都拥有一个极值点。垂直形、20°倾斜形、40°倾斜形元件的最大制冷量分别是1.320 6, 1.211 3, 1.081 6 W,而最大制冷量所对应的工作电流分别是23, 21以及19 A,对应的工作电压可由Mechanical模块计算得到,分别是137.89, 137.2, 139.06 mV。因此,可以认为,40°倾斜形能够取得的制冷量峰值最小,但消耗的功率也最小,为2.642 1 W;垂直形可取得的制冷量峰值最大,但须消耗最大的功率,为3.1715 W。进一步观察图 5还可以发现,当电流小于5 A时,制冷量由大到小分别是40°倾斜形、20°倾斜形、垂直形。所以得出结论:在小功率工况下,倾斜角度越大,制冷量越大。
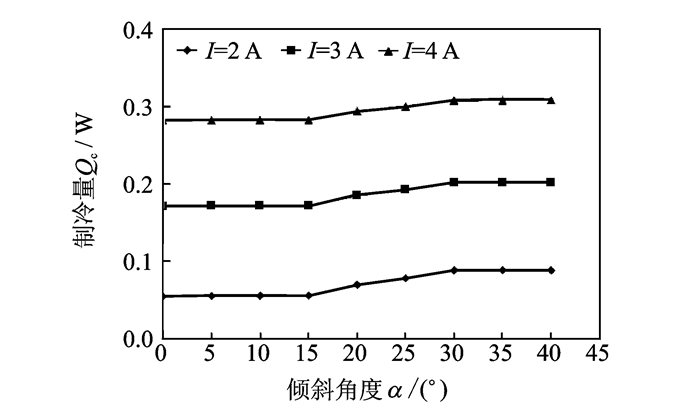
图 6分别展示了小工况下I=2, 3, 4 A时制冷量随倾斜角度的变化曲线,印证了两者之间的单调递增关系,同时发现,15°~30°倾角范围制冷量变化明显,梯度最大,而在其他倾角范围内制冷量变化并不显著,斜率近似为零。
|
图 6 制冷量随倾斜角度的变化关系 Figure 6 Cooling capacity versus slope |
控制电流一定,改变冷热端温差,得到3种不同热电元件的制冷量Qc随温差ΔT的变化关系。以小功率I=4.5 A为例,结果如图 7所示。
|
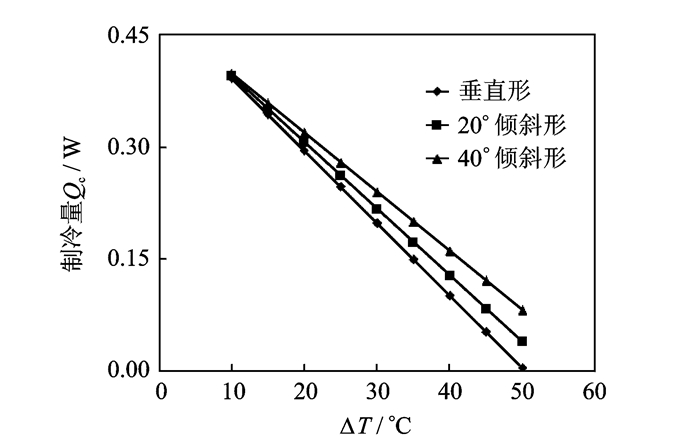
图 7 制冷量随温差的变化关系 Figure 7 Cooling capacity versus temperature difference |
3种热电元件的制冷量均随温差的增大而减小,其中40°倾斜形制冷量减小速率最慢,垂直形减小速率最快。制冷量由大到小依次是40°倾斜形、20°倾斜形和垂直形,且随着温差的增大,不同结构热电元件的制冷量之间的差值越来越大。当ΔT=10 ℃时,相比于垂直形,20°倾斜形的制冷量差值为0.028 4 W,而40°倾斜形的制冷量差值为0.054 3 W;当ΔT=50 ℃时,两者制冷量差值又分别是0.034 6 W和0.077 6 W。因此,在确定温差的前提下,倾斜角度越大,制冷量越大,元件越具优势,并且随着温差增大,优势越明显。
3.3 制冷系数分析制冷系数COP是评价热电制冷器工作性能的一项重要指标。本文仍以温差ΔT=20 ℃为例,研究对比倾斜角度对制冷系数的影响,模拟结果如图 8所示。
|
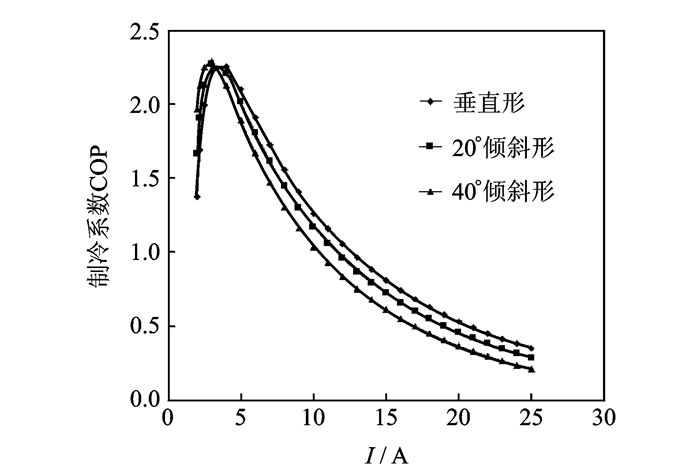
图 8 制冷系数随电流的变化关系 Figure 8 Coefficient of performance versus current |
随着电流的增大,制冷系数均先增大后减小,每条变化曲线都有一条峰值。垂直形、20°倾斜形、40°倾斜形的最高制冷系数分别是2.252 8, 2.267 5和2.287 1,对应的电流、电压值又分别是4, 3.3和3 A和31.325, 29.854和29.444 mV。从中可以发现,40°倾斜形最高制冷系数最大,而垂直形最低。同时,40°倾斜形达最高制冷系数所需功率最小,为0.088 3 W,而垂直形所需功率最大,为0.125 3 W。进一步观察图 8还可以发现,当电流小于3 A时,40°倾斜形制冷系数最高,而垂直形最低;当电流大于3 A时,垂直形制冷系数最高,而40°倾斜形最低。因此,可以认为,40°倾斜形适用于小功率工况,而垂直形适用于大功率工况。
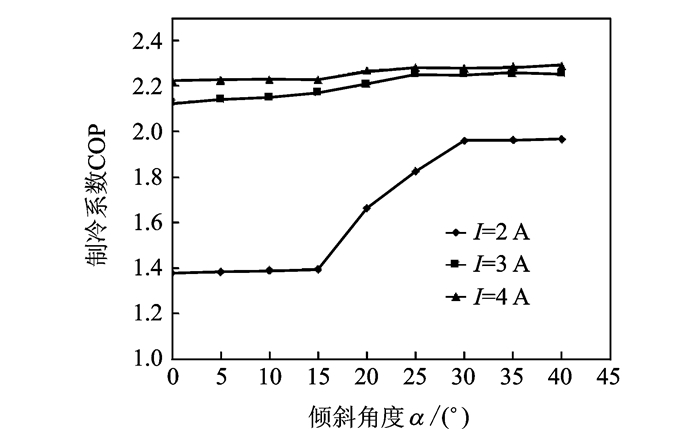
在既有基础上进一步改变倾斜角度,分析不同倾角所对应的制冷系数。如图 9所示,可以证明,倾斜角度越大,元件制冷效率越高;而且,15°~30°倾角对热电元件影响最大;最后也应注意,当系统达到一定功率,倾角产生的影响将大大减弱,即对比I=2, 4 A两个工况,I=4 A时制冷系数的变动幅度远小于I=2 A工况,这也从侧面印证了倾斜结构更适用于小功率情形。
|
图 9 制冷系数随倾斜角度的变化关系 Figure 9 Coefficient of performance versus slope |
3.4 电场分析
采用ANSYS Workbench中的热电耦合模块——Thermal-Electric,不仅可以模拟温度场分布状况,获取温度、热流量等物理参数,还能够实现电场的仿真,从而进行多物理场耦合分析[15]。现针对垂直形、40°倾斜形两种结构的热电元件,均通以I=3 A的电流,控制冷热端温差ΔT=20℃,得到电势分布云图,如图 10所示。分析对比发现,两种热电元件的电势在X轴上均不发生变化,而且铜片中的电势均匀分布。在垂直形元件中,从N型半导体经铜片至P型半导体,电势逐渐减小;在半导体中,电势在Z轴方向上一维变化。

|
图 10 热电元件的电势分布云图 Figure 10 Potential distribution nephogram of thermoelectric element |
在倾斜形元件中,半导体区域电势是关于Y, Z的函数,不同半导体中的变化趋势恰巧相反。进一步观察倾斜形半导体中电势分布,不难发现,在半导体侧棱方向上,电势可以看成一维线性变化。
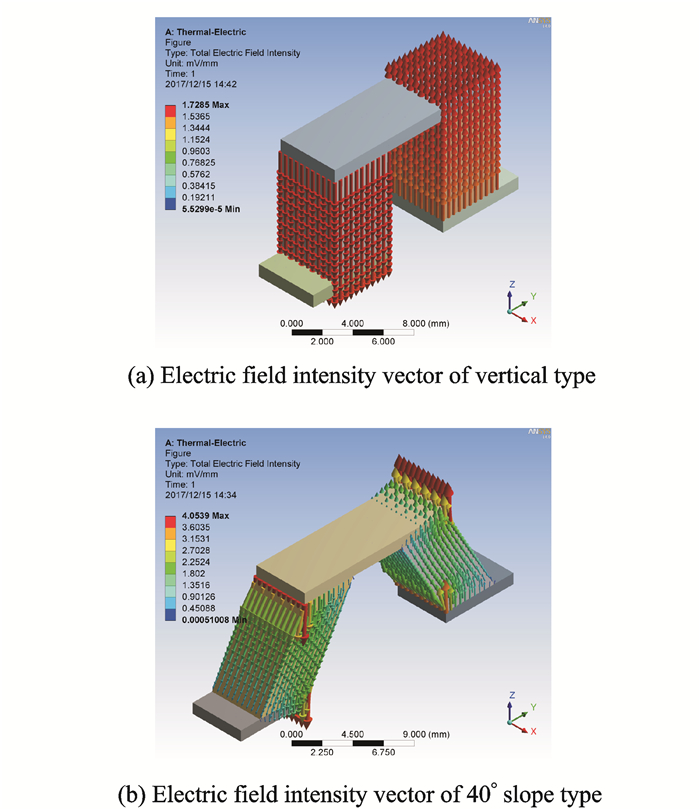
下面分析电场强度,如图 11所示为两种热电元件的电场强度矢量分布图。
|
图 11 热电元件的电场强度矢量图 Figure 11 Electric field intensity vector of thermoelectric element |
观察矢量图可以发现,电场强度主要分布在半导体中,而3块铜片中的电场强度却很小,近似为零。这主要是因为铜片电阻小,电势下降幅度小,即图 10所示,可以认为每块铜片中的电势等值分布,不存在电势梯度。垂直形元件中半导体内的电场强度分布较为均匀,大小1.7 mV/mm左右,方向竖直。这主要是由于半导体内的电势沿Z轴或-Z轴一维线性变化,即图 10(a)所示,因此形成均匀的电势梯度。40°倾斜形元件,如图 11(b)所示,半导体除绝大部分区域电场强度分布均匀外,上下端倾斜角处电场强度发生突变,最高达到4.05 mV/mm,远大于元件其他区域。这主要是因为半导体电臂的倾斜布置,倾角处的电势梯度陡然增大,所以电场强度大小发生突变。但同样是倾斜角,元件上侧的内部倾斜角和下侧的外部倾斜角不存在场强突变,电场强度反而接近于零。其中的缘由可参考图 10(b),上述4处倾斜角周围的电势并没有发生变化,所以电势梯度为0,即电场强度为0。
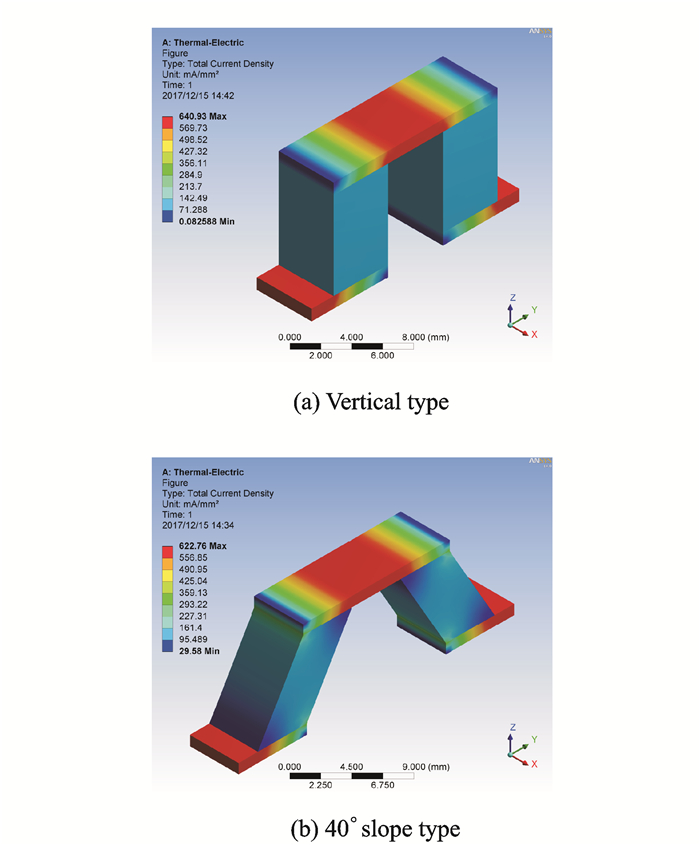
最后讨论电流密度,如图 12所示为3种热电元件的电流密度分布云图。
|
图 12 热电元件的电流密度分布云图 Figure 12 Current density distribution of thermoelectric element |
通过分析对比发现,两种热电元件有着相似的电流密度分布规律。元件上侧铜片的中间部分与下侧铜片外边缘的电流密度最大,达到620 mA/mm2以上。这主要是因为铜片厚度小,所以电流通过的区域电流密度大。上侧铜片外边缘与下侧铜片内边缘的电流密度最小,近似为0。这是由于上述区域并不能与外界形成通路,所以没有电流通过。在垂直形元件中,两半导体内的电流密度处处相等,而在倾斜形元件中,伴随倾斜结构的缘故,斜角处没有电流通过,电流密度小于其他区域。
4 结论本文保持相同材料用量,提出了倾斜结构的热电元件,采用数值模拟的方法对其进行了多物理场耦合分析,重点研究了倾斜角度对元件制冷性能的影响,所得结论主要有:
(1) 倾斜角度越大,热电元件能够达到越低的冷端温度;(2)小功率条件下增大倾斜角,有利于增大制冷量,提高制冷系数;(3)倾斜结构元件的最佳倾角范围是15°~30°;(4)倾斜结构中存在电场强度突变,而垂直形结构并无此现象;(5)不同结构的电流密度分布规律相同,最大电流密度值均出现在铜片区域中。(6)小功率设备宜采用倾斜形结构。
本文研讨了倾斜结构热电元件的工作特点,对微小型、小功耗热电制冷设备的改进具有一定的指导意义。但是,文中只讨论了单个热电元件的工况,因此,整体热电组件的性能有待进一步的研究与分析。
| [1] |
王小群, 杜善义.
热电制冷技术在航空航天领域的应用[J]. 中国航天, 2006(10): 22–24.
DOI:10.3969/j.issn.1672-9463.2006.10.009 WANG Xiaoqun, DU Shanyi. Thermoelectric cooling technology applied in aerospace field[J]. Aerospace China, 2006(10): 22–24. DOI:10.3969/j.issn.1672-9463.2006.10.009 |
| [2] |
HEALTHCARE G.
2-D electrophoresis:Principles and methods[M]. USA: GE Healthcare Limited, 2007.
|
| [3] |
祝薇, 邓元, 王瑶, 等.
热电薄膜材料的制备和制冷器件的数值模拟[J]. 北京航空航天大学学报, 2015, 41(8): 1435–1442.
ZHU Wei, DENG Yuan, WANG Yao, et al. Preparation of thermoelectric thin film material and numerical simulation of cooler[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1435–1442. |
| [4] |
MCCARTY R.
A comparison between numerical and simplified thermoelectric cooler models[J]. Journal of Electronic Materials, 2010, 39(9): 1842–1847.
DOI:10.1007/s11664-010-1075-x
|
| [5] |
申利梅, 陈焕新, 梅佩佩, 等.
热电制冷模块热连接与电连接的性能优化分析[J]. 化工学报, 2012, 63(5): 1367–1372.
DOI:10.3969/j.issn.0438-1157.2012.05.006 SHEN Limei, CHEN Huanxin, MEI Peipei, et al. Optimization analysis on thermal connection and electrical connection of thermoelectric refrigeration modules[J]. CIESC Journal, 2012, 63(5): 1367–1372. DOI:10.3969/j.issn.0438-1157.2012.05.006 |
| [6] |
杨凡超, 王洪伟, 王彩玲, 等.
第二类边界条件下热电偶非均匀内热源的工程求解分析[J]. 红外与激光工程, 2013, 42(S1): 30–33.
YANG Fanchao, WANG Hongwei, WANG Cailing, et al. Engineering analysis of non-uniform internal heat source in the thermocouple under the second boundary condition[J]. Infrared and Laser Engineering, 2013, 42(S1): 30–33. |
| [7] |
CHANG N K, KIM J.
Numerical examination of the performance of a thermoelectric cooler with peltier heating and cooling[J]. Journal of Electronic Materials, 2015, 44(10): 1–6.
|
| [8] |
CAI Y, LIU D, ZHAO F Y, et al.
Performance analysis and assessment of thermoelectric micro cooler for electronic devices[J]. Energy Conversion & Management, 2016, 124: 203–211.
|
| [9] |
胡仁喜, 闫波.
ANSYS 15.0多物理耦合场有限元分析从入门到精通[M]. 3版. 北京: 机械工业出版社, 2015.
HU Renxi, Yan Bo. ANSYS 15.0 finite element analysis of multiphysics coupling field from entry to mastery[M]. 3rd ed. Beijing: China Machine Press, 2015. |
| [10] |
徐德胜.
半导体制冷与应用技术[M]. 2版. 上海: 上海交通大学出版社, 1999.
XU Desheng. Technology of semiconductor refrigeration and application[M]. 2nd ed. Shanghai: Shanghai Jiao Tong University Press, 1999. |
| [11] |
CHEN J, YU J, MA M.
Theoretical study on an integrated two-stage cascaded thermoelectric module operating with dual power sources[J]. Energy Conversion & Management, 2015, 98: 28–33.
|
| [12] |
申利梅, 陈焕新, 张威, 等.
影响热电制冷性能的关键因素及其分析[J]. 红外与激光工程, 2011, 40(10): 1866–1872.
DOI:10.3969/j.issn.1007-2276.2011.10.008 SHEN Limei, CHEN Huanxin, ZHANG Wei, et al. Analysis of the crucial factors affecting the performance of thermoelectric cooling[J]. Infrared and Laser Engineering, 2011, 40(10): 1866–1872. DOI:10.3969/j.issn.1007-2276.2011.10.008 |
| [13] |
WANG X D, HUANG Y X, CHENG C H, et al.
A three-dimensional numerical modeling of thermoelectric device with consideration of coupling of temperature field and electric potential field[J]. Energy, 2012, 47(1): 488–497.
DOI:10.1016/j.energy.2012.09.019
|
| [14] |
CHEN W H, LIAO C Y, HUNG C I.
A numerical study on the performance of miniature thermoelectric cooler affected by Thomson effect[J]. Applied Energy, 2012, 89(1): 464–473.
DOI:10.1016/j.apenergy.2011.08.022
|
| [15] |
许京荆.
ANSYS 13.0 Workbench数值模拟技术[M]. 北京: 中国水利水电出版社, 2012.
XU Jingjing. ANSYS 13.0 workbench numerical simulation technology[M]. Beijing: China Water & Power Press, 2012. |
 2018, Vol. 50
2018, Vol. 50


