2. 南京机电液压工程研究中心, 南京, 211100;
3. 南京航空航天大学航空宇航学院, 南京, 210016
2. Nanjing Engineering Institute of Aircraft Systems, Nanjing, 211100, China;
3. College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
现代飞机的安全问题一直受到社会的广泛关注,而燃油系统燃烧、爆炸是引起飞机失事的主要原因之一[1]。有数据表明,在越南战争中,美国空军由于受到地面火力攻击而损失了数千架飞机。在这些损失中,由于燃油失火导致的损失比例高达50%[2]。机舱安全研究技术小组(Cabin safety research technical group, CSRTG)对从1966到2009年全世界3 726起民机事故统计结果显示,共有370起事故与油箱燃烧爆炸有关。由此可见,无论对于军机还是民机,都必须采用有效的措施来防止油箱燃爆。飞机油箱的防火抑爆能力不仅关系到飞机的生存能力和易损性,同时也关系到飞机的利用率、成本和乘客的安全。
因此,从20世纪80年代开始,美国就着手进行了燃油箱惰化技术的研究,以充分抑制飞机燃油箱燃爆事故的发生[3-4]。随着国产大飞机项目的投产和新型战机的研制,国内近年来也对燃油箱惰化技术进行了大量的研究,例如对核心部件分离膜的性能进行了理论和实验研究[5-6],对冲洗和洗涤两种惰化技术的性能进行了比较[7],特别通过数学仿真的方式对富氮气体流量需求和惰化效果进行了计算分析[8-10]。
但是,目前对冲洗惰化的仿真大多集中在单隔仓油箱,而对于多隔仓油箱的仿真则需要分为地面、爬升和俯冲等几个过程[11],特别是模拟计算中大多认为进入油箱的富氮气体浓度恒定[10, 12],没有考虑分离膜在不同阶段由于模式不同或入口压力等参数的变化造成的富氮气体浓度和流量变化,从而对油箱惰化过程所产生的影响。
鉴于此,本文在介绍单流和双流冲洗惰化工作流程的基础上,建立一个通用的多隔仓油箱冲洗惰化数学模型,其无需将飞行过程区分为地面、爬升、巡航和下降等各个阶段,并给出模型求解方法。选择一个4隔仓燃油箱作为研究对象,在考虑飞行包线和耗油顺序的基础上,分别采用单流和双流模式进行惰化,分析油箱平均氧浓度和每个隔仓中氧浓度的变化。
1 单流和双流冲洗惰化描述惰化系统中,空气从发动机或者环控系统引入,稳压后经过过滤降温进入分离膜组件,根据分离膜产生的富氮气体进入燃油箱的方式,可分为单流模式和双流模式,如图 1所示。在图 1(a)所示的单流模式中,富氮气体通过限流孔后全部进入油箱,而图 1(b)所示的双流模式中,富氮气体分为两路,一路通过控制阀,而另外一路与其并联,通过切换控制阀的开启,可以实现两种流量的切换。通常,在地面滑行、爬升和巡航阶段关闭控制阀,这样产生的富氮气体流量小纯度高,而在俯冲下降时,则开启控制阀,由于流通面积增加,富氮气体流量大纯度低。目前,这两种设计方式在不同飞机中均有应用,例如Parker公司所设计的惰化系统大多采用双流模式,而Eaton公司则在某些设计中采用单流模式。
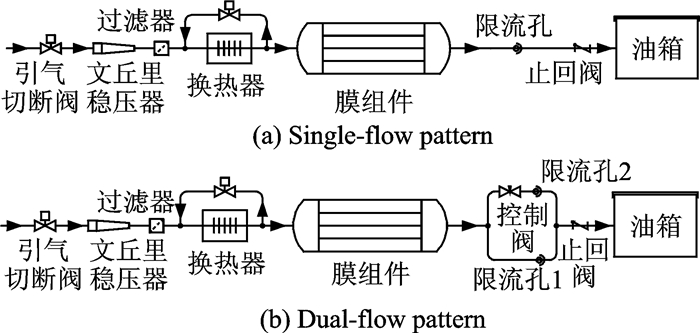
|
图 1 两种冲洗惰化模式示意图 Figure 1 Schematic diagram of two washing inerting modes |
2 数学模型建立
为了简化研究的复杂性,在建立模型前,提出以下合理假设:
(1) 富氮气体、气相空间中的氧气和氮气及其混合气体均视为理想气体;
(2) 忽略油箱中的燃油蒸气和其他微量气体影响;
(3) 冲洗过程中,恢复平衡状态所需的弛豫时间远远小于计算步长;
(4) 计算步长内,各种气体充分混合,气体内部各处的温度、压力和密度状态参数相同;
(5) 不考虑气体和燃油之间的换热;
(6) 仅考虑孔口的局部阻力,忽略管路流动阻力;
(7) 在任意压力下,ASM(Air separation module)产生的富氮气体质量流率恒定。
如图 2所示,对于一个燃油箱每个隔仓而言,其可能存在富氮气体冲洗口、向外界环境的排气口及与其他油箱的连通口。假设有N个隔仓,选择其中第i个隔仓,该隔仓与其他隔仓之间的氧氮流动方向及流量与相互之间的压力相关。
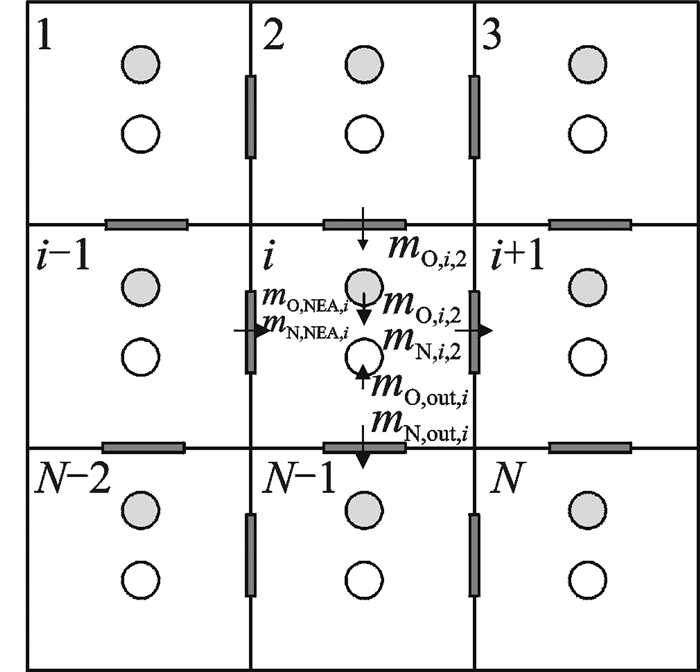
|
图 2 通用燃油箱中隔仓流量关系示意图 Figure 2 Diagram of flow relationship in compartments of general fuel tank |
当pi> pj,其中j=1, 2, …, N,j≠i,则有
| $ \frac{{{\rm{d}}{m_{i,j}}}}{{{\rm{d}}t}} = - \alpha {A_{i,j}}{\left[ {2{p_i}{\rho _i}\left( {{p_i} - {p_j}} \right)} \right]^{\frac{1}{2}}} $ | (1) |
| $ \frac{{{\rm{d}}{m_{{\rm{O}},i,j}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{i,j}}}}{{{\rm{d}}t}}{a_{{\rm{O}},i}} $ | (2) |
| $ \frac{{{\rm{d}}{m_{{\rm{N}},i,j}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{i,j}}}}{{{\rm{d}}t}}{a_{{\rm{N}},i}} $ | (3) |
当pi≤pj,则有
| $ \frac{{{\rm{d}}{m_{i,j}}}}{{{\rm{d}}t}} = \alpha {A_{i,j}}{\left[ {2{p_j}{\rho _j}\left( {{p_j} - {p_i}} \right)} \right]^{\frac{1}{2}}} $ | (4) |
| $ \frac{{{\rm{d}}{m_{{\rm{O}},i,j}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{i,j}}}}{{{\rm{d}}t}}{a_{{\rm{O}},j}} $ | (5) |
| $ \frac{{{\rm{d}}{m_{{\rm{N}},i,j}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{i,j}}}}{{{\rm{d}}t}}{a_{{\rm{N}},j}} $ | (6) |
式中:α为孔口的流量系数;Ai, j为第i个隔仓与第j个隔仓之间的连通面积,如果隔仓之间没有连通关系,则设置Ai, j为0;ρi和ρj分别为第i和第j个隔仓中气体的密度;aO和aN分别为氧氮的质量分数。此外,认为流入隔仓流量为正,流出为负。
第i个隔仓通过排气孔口向外界环境流出或从外界环境流入的气体也与压力相关。
如果pi >pt,即隔仓中压力高于外界压力,则
| $ \frac{{{\rm{d}}{m_{{\rm{out}},i}}}}{{{\rm{d}}t}} = - \alpha {A_{{\rm{out}},i}}{\left[ {2{p_i}{\rho _i}\left( {{p_i} - {p_{\rm{t}}}} \right)} \right]^{\frac{1}{2}}} $ | (7) |
| $ \frac{{{\rm{d}}{m_{{\rm{O,out}},i}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{{\rm{out}},i}}}}{{{\rm{d}}t}}{a_{{\rm{O}},i}} $ | (8) |
| $ \frac{{{\rm{d}}{m_{{\rm{N,out}},i}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{{\rm{out}},i}}}}{{{\rm{d}}t}}{a_{{\rm{N}},i}} $ | (9) |
如果当pi ≤pt,则外界空气流入隔仓
| $ \frac{{{\rm{d}}{m_{{\rm{out}},i}}}}{{{\rm{d}}t}} = \alpha {A_{{\rm{out}},i}}{\left[ {2{p_{\rm{t}}}{\rho _{{\rm{O}},{\rm{t}}}}\left( {{p_{\rm{t}}} - {p_i}} \right)} \right]^{\frac{1}{2}}} $ | (10) |
| $ \frac{{{\rm{d}}{m_{{\rm{O,out}},i}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{{\rm{out}},i}}}}{{{\rm{d}}t}}{a_{{\rm{O}},{\rm{air}}}} $ | (11) |
| $ \frac{{{\rm{d}}{m_{{\rm{N,out}},i}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{m_{{\rm{out}},i}}}}{{{\rm{d}}t}}{a_{{\rm{N}},{\rm{air}}}} $ | (12) |
第i个隔仓燃油中溶解氧氮的逸出速率为
| $ \frac{{{\rm{d}}{m_{{\rm{O}},{\rm{F}},i}}}}{{{\rm{d}}t}} = \frac{{{\beta _{\rm{O}}}}}{{{R_{\rm{O}}}{T_{\rm{F}}}}}\frac{{{\rm{d}}\left( {{V_{\rm{F}}}{p_{{\rm{O}},i}}} \right)}}{{{\rm{d}}t}} $ | (13) |
| $ \frac{{{\rm{d}}{m_{{\rm{N}},{\rm{F}},i}}}}{{{\rm{d}}t}} = \frac{{{\beta _{\rm{N}}}}}{{{R_{\rm{N}}}{T_{\rm{F}}}}}\frac{{{\rm{d}}\left( {{V_{\rm{F}}}{p_{{\rm{N}},i}}} \right)}}{{{\rm{d}}t}} $ | (14) |
式中: βO和βN分别为氧氮的阿斯特瓦尔德系数,其含义可参看文献[13];RO和RN分别为氧氮的气体常数;TF和VF分别为燃油温度和体积。
第i个隔仓中气相空间氧氮质量变化率为
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}{m_{{\rm{O}},{\rm{U}},i}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {{p_{{\rm{O}},i}}{V_{\rm{U}}}} \right)}}{{{R_{\rm{O}}}{T_{\rm{U}}}{\rm{d}}t}} = }\\ {\frac{{{\rm{d}}{m_{{\rm{O}},i,j}}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}{m_{{\rm{O}},{\rm{out}},i}}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}{m_{{\rm{O}},{\rm{F}},i}}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}{m_{{\rm{O}},{\rm{NEA}},i}}}}{{{\rm{d}}t}}} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}{m_{{\rm{N}},U,i}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {{p_{{\rm{N}},i}}{V_{\rm{U}}}} \right)}}{{{R_{\rm{N}}}{T_{\rm{U}}}{\rm{d}}t}} = \frac{{{\rm{d}}{m_{{\rm{N}}.i.j}}}}{{{\rm{d}}t}} + }\\ {\frac{{{\rm{d}}{m_{{\rm{N}},{\rm{out}},i}}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}{m_{{\rm{N}},{\rm{F}},i}}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}{m_{{\rm{N}},{\rm{NEA}},i}}}}{{{\rm{d}}t}}} \end{array} $ | (16) |
式中:TU和VU分别为气相空间温度及体积,显然隔仓的总体积Vi=VF+ VU。
理论上,富氮气体流量与限流孔尺寸及进入隔仓的冲洗口面积ANEA, i相关,但是通常限流孔的直径远小于冲洗口的直径,而隔仓中的压力相对于分离膜组件的出口压力而言很小,因此限流孔基本处于阻塞工况,即总的富氮气体流量mNEA仅与分离膜出口压力相关,故此可按照喷管阻塞流动模型来计算富氮气体总流量
| $ {{\dot m}_{{\rm{NEA}}}} = \frac{{{\rm{d}}{m_{{\rm{NEA}}}}}}{{{\rm{d}}t}} = \alpha '{A_{{\rm{or}}}}{\left[ {\frac{{2k{p_{\rm{m}}}{\rho _{\rm{m}}}}}{{k - 1}}\left( {p_{{\rm{cr}}}^{\frac{2}{k}} - p_{{\rm{cr}}}^{\frac{{k + 1}}{k}}} \right)} \right]^{\frac{1}{2}}} $ | (17) |
式中:α′为喷管流量系数;k为富氮气体绝热指数,可按空气选取为1.4;Aor为限流孔面积,在单流模式中Aor=Asmall,而双流模式下当控制阀开启后Aor=Asmall+Alarge;pm和ρm分别为分离膜出口富氮气体压力和密度,pcr为临界压力比,其值为
| $ {p_{{\rm{cr}}}} = {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}} $ | (18) |
进入每个隔仓的富氮气体流量简单假设仅与冲洗口面积比相关,因此有
| $ \frac{{{\rm{d}}{m_{{\rm{O}},{\rm{NEA}},i}}}}{{{\rm{d}}t}} = {a_{{\rm{O}},{\rm{NEA}}}}\frac{{{A_{{\rm{NEA}},i}}}}{{\sum\limits_{i = 1}^N {{A_{{\rm{NEA}},i}}} }}\frac{{{\rm{d}}{m_{{\rm{NEA}}}}}}{{{\rm{d}}t}} $ | (19) |
| $ \frac{{{\rm{d}}{m_{{\rm{N}},{\rm{NEA}},i}}}}{{{\rm{d}}t}} = {a_{{\rm{N}},{\rm{NEA}}}}\frac{{{A_{{\rm{NEA}},i}}}}{{\sum\limits_{i = 1}^N {{A_{{\rm{NEA}},i}}} }}\frac{{{\rm{d}}{m_{{\rm{NEA}}}}}}{{{\rm{d}}t}} $ | (20) |
富氮气体的纯度与富氮气体流量、分离膜入口温度压力及飞行高度相关,可根据实验数据拟合[14-15],但是考虑到一般温度固定,而飞行高度影响不显著,因此富氮气体摩尔分数与分离膜出口富氮气体流量及压力的关系可以表达为
| $ {x_{\rm{N}}} = \sum\limits_{k = 0}^2 {\dot m_{{\rm{NEA}}}^k} \sum\limits_{l = 0}^2 {{\gamma _{k,l}}p_m^l} $ | (21) |
制氮效率可表达为
| $ \eta = \sum\limits_{k = 0}^2 {\dot m_{{\rm{NEA}}}^k} \sum\limits_{l = 0}^2 {{\chi _{k,l}}p_m^l} $ | (22) |
式中:γk, l和χk, l为拟合系数。
计算的初始条件为
| $ {p_i} = {p_{\rm{t}}}\left| {_{{\rm{t}} = 0}} \right. $ | (23) |
环境压力随高度的变化为
| $ {p_{\rm{t}}} = 6894.757 \times {10^{1.167\;199 + 5.255\;3\log 10\left( {1 - 0.006\;879\;17H} \right)}} $ | (24) |
选择的油箱如图 3所示[16-17],共有4个隔仓和1个通气箱组成,隔仓的编号如图所示,隔仓1体积为5.06m3,隔仓2体积为1 070 L,隔仓3体积为320 L,隔仓4体积为265 L,通气箱体积为220 L。富氮气体流入油箱又分成两种分配方式,即串联进气和并联进气,所谓串联进气就是富氮气体全部进入隔仓2,然后通过连通口顺次流经隔仓3、隔仓4、隔仓1和通气箱后最终流出至外界环境,而并联进气是将富氮气体同时通入所有隔仓中,且每个隔仓中的进气量相同。
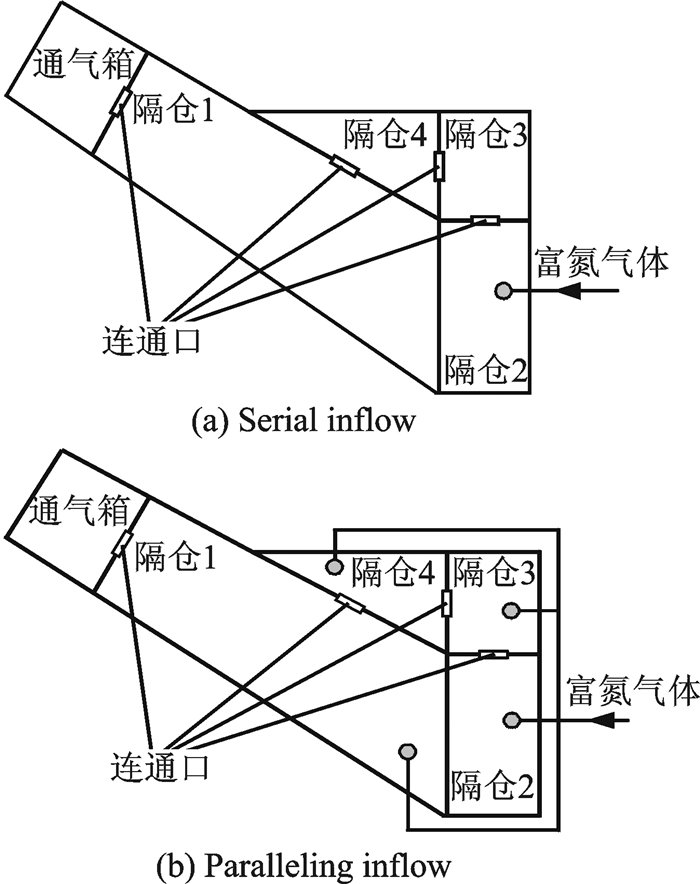
|
图 3 油箱拓扑结构及富氮气体分配方式示意图 Figure 3 Schematic diagram of fuel tank topological structure and NEA distribution modes |
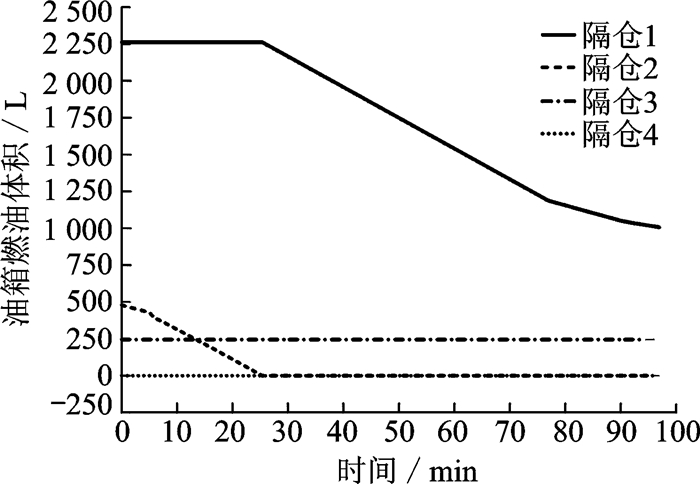
计算中选择的飞行包线、发动机引气压力和燃油消耗率如图 4所示,隔仓1至隔仓4的初始载油量分别为1 940, 410, 245和0 kg,耗油按照隔仓2→隔仓1→隔仓3的顺序进行,因此隔仓中燃油体积随时间的变化关系如图 5所示。
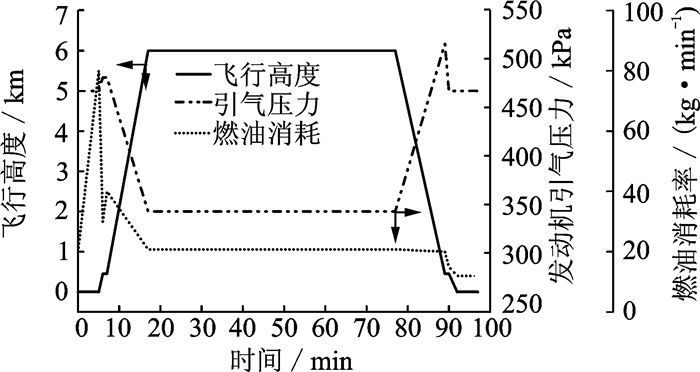
|
图 4 飞行包线、燃油消耗率及膜后压力随时间变化 Figure 4 Variation of flight envelope, fuel consumption rate and pressure behind membrane with time |
|
图 5 各隔仓中油量随时间变化关系 Figure 5 Variation of fuel in each compartment with time |
3.2 分离膜工作特性
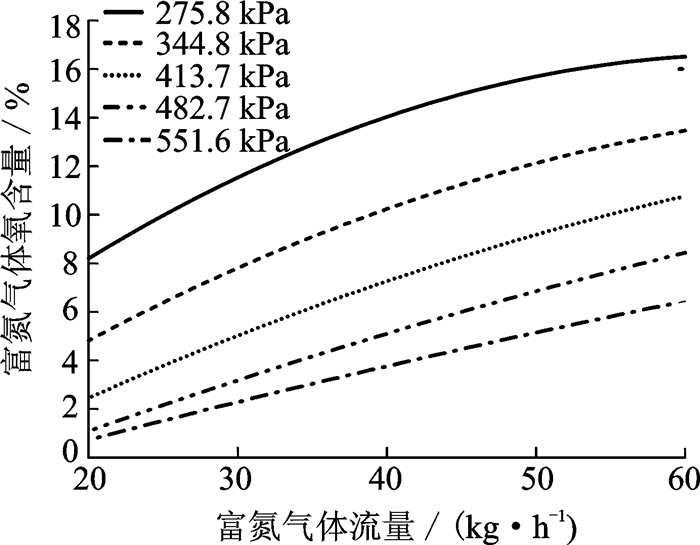
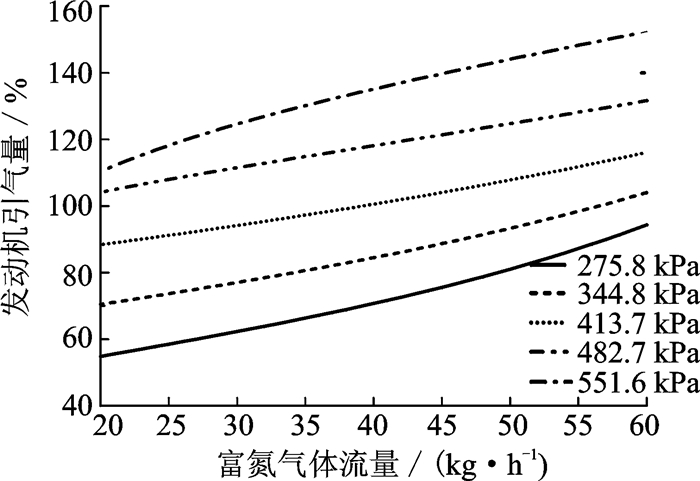
选择某型分离膜,并根据实验数据对其按照式(21)和式(22)的要求进行拟合,最终得到的系数如表 1所示。图 6和图 7分别给出了该分离膜在不同压力下的分离性能。
| 表 1 分离膜性能公式所用系数 Table 1 Coefficientsused in the performance formula of the separation membrane |
|
图 6 不同入口压力下富氮气体浓度随流量变化关系 Figure 6 Variation of NEA concentration under different inlet pressures with flow |
|
图 7 不同入口压力下发动机引气量随流量变化关系 Figure 7 Variation of engine bleed air value under different inlet pressures with flow |
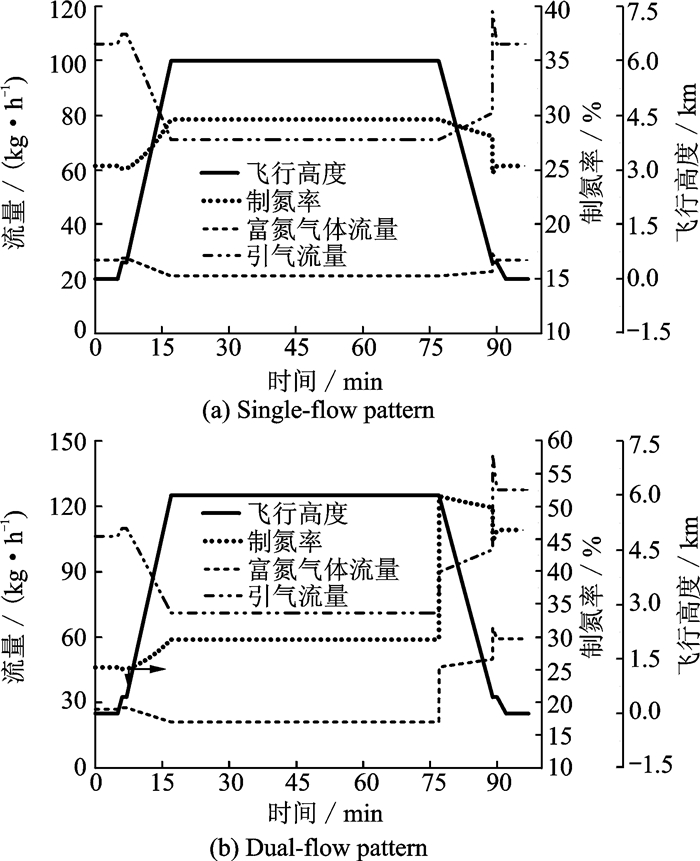
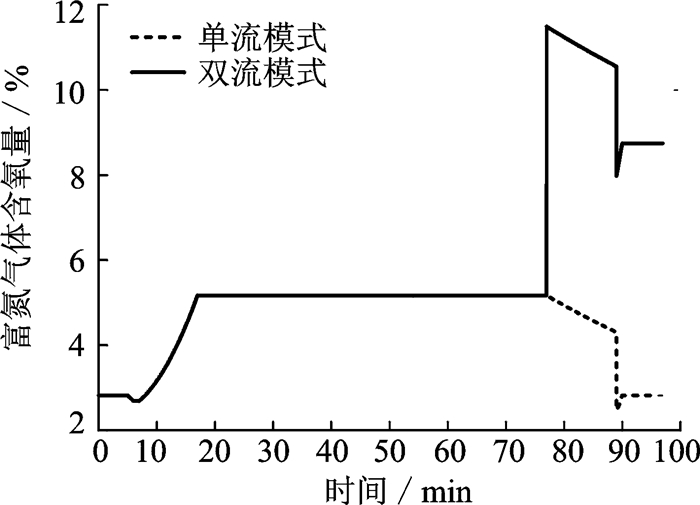
图 1(a)单流模式中限流孔尺寸为3.2 mm,图 1(b)双流模式中限流孔1尺寸为3.2 mm,限流孔2尺寸为3.5 mm。当第80 min开始俯冲下降时,图 1(b)中的控制阀打开,进入大流量模式。图 8给出了两种模式下,富氮气体和发动机引气流量在飞行包线不同时候的变化关系,从图中可以明显看出,在双流模式下,俯冲下降时富氮气体流量显著增加,从图 9可见,这时富氮气体的纯度会降低。此外,从图 8还可以发现,双流模式下俯冲下降时最大引气流量约为140 kg/h,略大于单流模式时的最大引气流量(约120 kg/h),显然增加的量并不大。
|
图 8 富氮气体和引气流量随时间变化关系 Figure 8 Variation of NEA and bleed air flow with time |
|
图 9 富氮气体浓度随时间变化关系 Figure 9 Variation of NEA concentration with time |
4 计算结果及分析
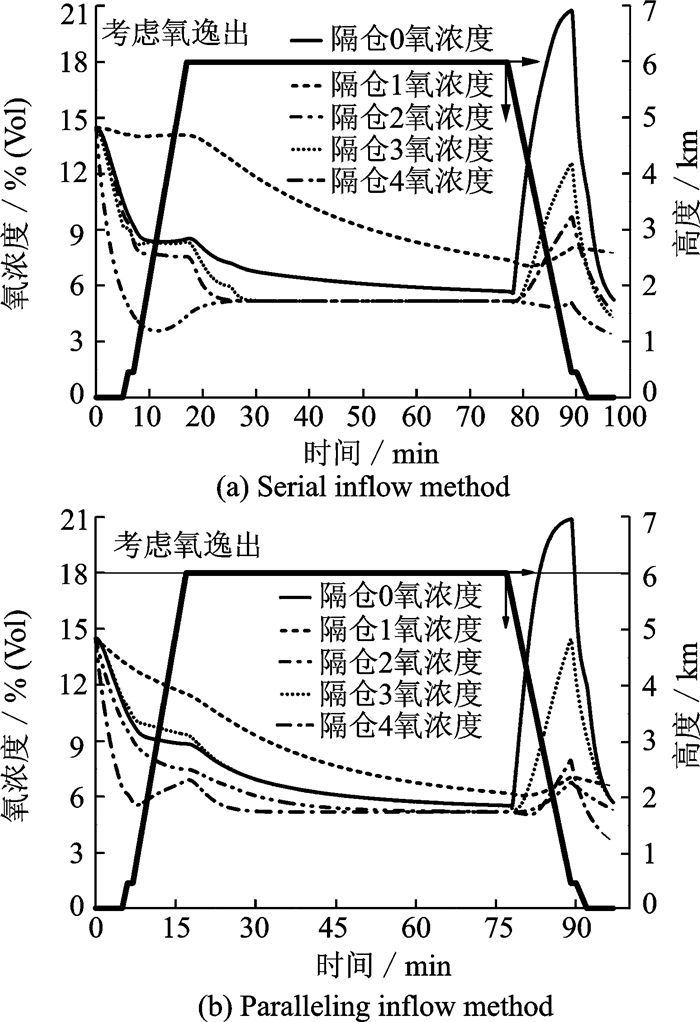
图 10给出了串联和并联进气方式下,单流量模式中油箱各隔仓气相空间氧浓度随时间的变化关系。从图 10(a)中可见,串联进气时,所有的富氮气体均首先进入隔仓2,因此隔仓2中氧浓度会迅速降低。而富氮气体最后流入隔仓1,且流入的是与其他隔仓气相空间气体混合后的富氮气体,因此隔仓1惰化效果最差。从图 10(b)中可见,并联进气后,所有的富氮气体同时进入所有隔仓中,因此与串联进气相比,各隔仓氧浓度变化差异会减少,但是由于每个隔仓所分配的富氮气体流量一样,但是隔仓的容积和载油量有差异,故此隔仓1惰化最慢,而隔仓4由于容积很小故惰化十分迅速。
|
图 10 单流模式下各隔仓中氧浓度随时间变化关系 Figure 10 Variation of Oxygen concentration in each compartment with time under single-flow pattern |
从图 10中还可以发现,俯冲下降时,由于外界环境压力升高,空气会通过通气箱进入油箱中,因此通气箱氧浓度迅速升高,由于单流模式中,分离膜产生的富氮气体流量较少,不足以弥补压力变化后隔仓中所需填补的气体质量变化,因此无法阻止通气箱中的气体向隔仓中流动,造成隔仓中的氧浓度升高。显然,隔仓的气相空间越大,则抵御外界空气进入后造成氧浓度升高的能力越强,故此从图 10中可以发现,隔仓1和隔仓2氧浓度升高幅度小,而隔仓3和隔仓4则升高较多。在单流模式下,通气箱和隔仓3均出现了超标,即氧浓度大于12%。此外,对比图 10(a)和图 10(b)可以发现,在串联进气时,由于所有富氮气体均流入隔仓2,因此俯冲下降开始阶段,隔仓2的氧浓度不仅没有上升,还在持续下降。
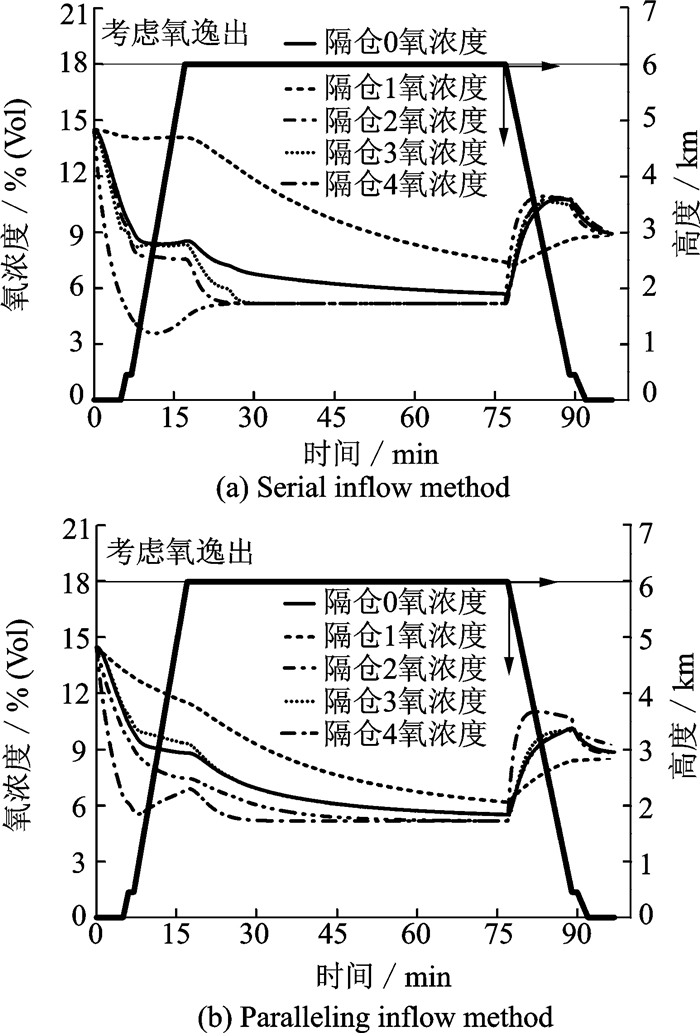
图 11中计算了双流模式中两种进气方式下,各隔仓的氧浓度变化。从图中可见,在俯冲下降前,双流模式中氧浓度变化与单流模式完全相同,但是俯冲下降后,由于双流模式中控制阀打开,产生更多的富氮气体,可阻止外界空气进入油箱。对照图 9可以发现,由于富氮气体流量增加,富氮气体中含氧量增加,因此图 11俯冲下降时隔仓氧浓度增加并非是外界空气进入造成,而是由于富氮气体中氧浓度增加所造成。对比图 11(a)和图 11(b)可见,并联进气方式要略好于串联进气方式。
|
图 11 双流模式下各隔仓中氧浓度随时间变化关系 Figure 11 Variation of Oxygen concentration in each compartment with time under dual-flow pattern |
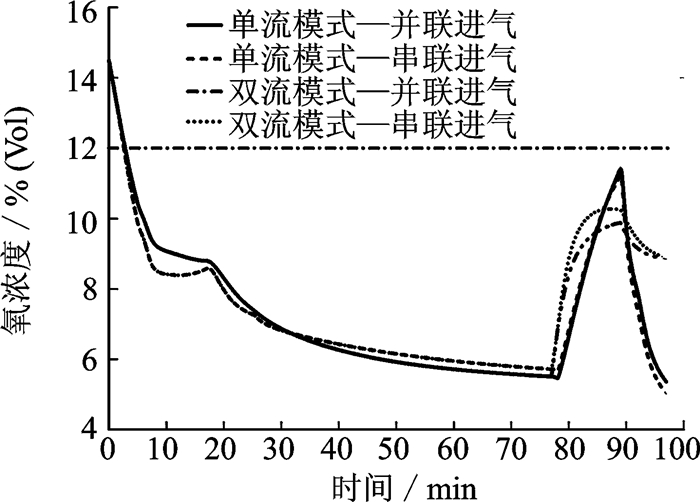
图 12给出了单流和双流模式下两种进气方式时,油箱中所有隔仓中的平均氧浓度。从图中可见,在俯冲下降前,平均氧浓度基本一致。串联进气方式在俯冲下降前能达到的氧浓度略高于并联方式。单流模式下,俯冲下降时,串联进气时氧浓度要高于并联进气方式。双流模式下,俯冲下降时,串联和并联两种进气方式基本没有差异。
|
图 12 油箱平均氧浓度随时间的变化关系 Figure 12 Variation of average oxygen concentration in fuel tank with time |
5 结论
(1) 在进行了一定合理简化的基础上,本文建立了隔仓通用的数学模型,可对多隔仓油箱的惰化过程进行分析计算。选择了一个具有4个隔仓的油箱为研究对象,选定了单流和双流模式下限流孔的尺寸,以某分离膜实验数据回归了分离膜性能公式所用系数,计算分析了串联和并联方式下隔仓中氧浓度随时间的变化关系。研究结果显示,单流模式和双流模式均具有各自的优缺点,单流模式流程相对简单,无需设置双流量控制阀,但是单流模式很难避免俯冲下降阶段外部空气进入油箱所造成的油箱局部氧浓度超标,而双流模式则可以避免此现象发生,但是需要设置双流量控制阀,增加了系统的复杂性。
(2) 本文研究表明,串联和并联进气方式对隔仓中氧浓度的影响并不大。在双流模式下,并联进气略好于串联进气方式。相对而言,串联方式管路布置更加简单。
(3) 本文研究认为氧氮按照平衡关系完全逸出,这与实际情况存在较大的差异,因此在后续的研究中,应该按照实际情况考虑氧氮的逸出速率。
| [1] |
王小平, 肖再华.
飞机燃油箱氮气惰化的机理分析及应用[J]. 航空科学技术, 2008(8): 24–26.
WANG Xiaoping, XIAO Zaihua. Fundamentally analysis on inerting of aircraft fuel tank with nitrogen-enriched air and its application[J]. Aeronautical Science and Technology, 2008(8): 24–26. |
| [2] |
LANGTON R, CLARK C, HEWITT M, et al.
Aircraft fuel systems[M]. [S.1.]: Wiley Online Library, 2009.
|
| [3] |
DESMARAISLA, TOLLEFF, ALLENTD. E-valuation of advanced airplane fire extinguishants[C]//Proceedings of 19th AIAA, SAE, and ASME, JointPropulsion Conference. Seattle, WA: [s. n. ], 1983: 179-191. |
| [4] |
刘小芳, 刘卫华.
飞机供氧和燃油箱惰化技术概况[J]. 北华航天工业学院学报, 2008, 18(3): 4–7.
DOI:10.3969/j.issn.1673-7938.2008.03.002 LIU Xiaofang, LIU Weihua. Outline of airborne oxygen supplied and its fuel tanks inerted[J]. Journal of North China Institute of Aerospace Engineering, 2008, 18(3): 4–7. DOI:10.3969/j.issn.1673-7938.2008.03.002 |
| [5] |
冯诗愚, 卢吉, 刘卫华, 等.
机载制氮系统中空纤维膜分离特性[J]. 航空动力学报, 2012, 27(6): 1332–1339.
FENG Shiyu, LU Ji, LIU Weihua, et al. Separation performance of hollow fiber membrane for on-board inerting gas generating system[J]. Journal of Aerospace Power, 2012, 27(6): 1332–1339. |
| [6] |
邵垒, 刘卫华, 孙兵, 等.
中空纤维膜分离性能实验与预测[J]. 航空动力学报, 2015, 30(4): 800–806.
SHAO Lei, LIU Weihua, SUN Bing, et al. Experiment and prediction of separation performance of hoilow fiber membrane[J]. Journal of Aerospace Power, 2015, 30(4): 800–806. |
| [7] |
汪明明, 冯诗愚, 蒋军昌, 等.
飞机燃油箱冲洗与洗涤惰化技术比较分析[J]. 南京航空航天大学学报, 2010, 42(5): 614–619.
DOI:10.3969/j.issn.1005-2615.2010.05.014 WANG Mingming, FENG Shiyu, JIANG Junchang, et al. Comparative analysis of fuel washing and scrubbing in aircraft fuel tank[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(5): 614–619. DOI:10.3969/j.issn.1005-2615.2010.05.014 |
| [8] |
魏树壮, 刘卫华, 潘俊, 等.
油箱惰化流量需求计算方法研究[J]. 航空兵器, 2014(6): 45–49.
DOI:10.3969/j.issn.1673-5048.2014.06.010 WEI Shuzhuang, LIU Weihua, PAN Jun, et al. Study on calculation method of flow requirement for fuel tank inerting[J]. Aerp Weaponry, 2014(6): 45–49. DOI:10.3969/j.issn.1673-5048.2014.06.010 |
| [9] |
高秀峰, 刘卫华, 熊斌, 等.
飞机燃油箱冲洗惰化过程的理论研究[J]. 西安交通大学学报, 2010, 44(9): 16–20.
GAO Xiufeng, LIU Weihua, XIONG Bin, et al. Theoretical study on the process of aircraft fuel tank flushing[J]. journal of Xi'an Jiao Tong University, 2010, 44(9): 16–20. |
| [10] |
王志伟, 王学德, 刘卫华, 等.
不同进气方式对某民机中央翼油箱惰化性能的影响[J]. 安全与环境学报, 2012, 12(3): 172–176.
DOI:10.3969/j.issn.1009-6094.2012.03.041 WANG Zhiwei, WANG Xuede, LIU Weihua, et al. Influence of different distribution methods on the inerting process of a civil airplane center wing tank[J]. Journal of Safety and Environment, 2012, 12(3): 172–176. DOI:10.3969/j.issn.1009-6094.2012.03.041 |
| [11] |
冯晨曦. 民机油箱气相空间氧浓度控制技术研究[D]. 南京: 南京航空航天大学, 2012.
FENG Chenxi. Control technology of oxygen concentration on civil aircraft fuel tank ullage[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. |
| [12] |
冯晨曦, 刘卫华, 鹿世化, 等.
气体分配方式对多隔仓燃油箱地面惰化的影响[J]. 航空动力学报, 2011, 26(11): 2528–2533.
FENG Chenxi, LIU Weihua, LU Shihua, et al. Study on ground-based inerting process influenced by different gas distribution for multi-bay fuel tank[J]. Journal of Aerospace Power, 2011, 26(11): 2528–2533. |
| [13] |
Coordinating Research Council, INC. Handbook of aviation fuel properties -2004[R]. APRL-PR-WP-TR-2004-2127, 2004. |
| [14] |
邵垒, 刘卫华, 冯诗愚, 等.
机载空分装置富氮气体流量及影响因素[J]. 北京航空航天大学学报, 2015, 41(1): 141–146.
SHAO Lei, LIU Weihua, FENG Shiyu, et al. Flow rate of nitrogen-rich air and influence factors for on-board air separation unit[J]. Journal of Beijing University of Aeronautics Astronautics, 2015, 41(1): 141–146. |
| [15] |
AHMAD F, LAU K K, SHARIFF A M, et al.
Temperature and pressure dependence of membrane permeance and its effect on process economics of hollow fiber gas separation system[J]. Journal of Membrane Science, 2013, 430: 44–55.
DOI:10.1016/j.memsci.2012.11.070
|
| [16] |
WILLIAM M C, MORRISON R. Development and testing of the faa simplified fuel tank inerting system: DOT/FAA/AR-05/6[R]. Washington D C, USA: Office of Aviation Research, 2005. |
| [17] |
CAVAGE W Modeling inert gas distribution in commercial transport aircraft fuel tanks[R]. AIAA 2002-3032, 2002. |
 2018, Vol. 50
2018, Vol. 50


