声发射(Acoustic emission,AE)是材料内部快速释放应力能的一种现象,部分应力能以弹性波的形式从应力源辐射出来并且可以被安放在材料表面的声发射传感器探测到。在搅拌摩擦焊接(Friction stir welding,FSW)的过程中,由于材料发生塑性变形而产生大量声发射信号,利用该技术可以在线监测搅拌摩擦焊连接过程中的声发射信号。
目前国内外学者通过对FSW焊接过程中的声发射信号进行采集与分析来研究焊接质量与信号特征值之间的关系[1],其目的都是为了预测和改善焊接接头的质量[2]。Subramaniam等人[3]利用声发射技术监测和分析了搅拌针轮廓形状对焊接接头抗拉强度的影响,对不同参数下声发射信号特征与焊接接头抗拉强度的相关性进行了研究。Soun dararajan等人[4]将声发射技术应用于监测搅拌摩擦焊接过程,研究了不同下压量及焊接速度下的声发射信号变化情况,通过对原始信号进行快速傅立叶变换得出声发射信号在频域中振幅的变化受工具下压量影响较大。Suresha等人[5]开发了基于声发射的搅拌摩擦焊质量预测概念模型,将FSW工艺参数、工具轮廓、材料流动模式、微结构和机械性能等与声发射信号特征相关联,以帮助监视和控制焊接质量。
在搅拌摩擦焊接过程中由于摩擦、热变形使得搅拌工具磨损严重,不同形状的搅拌针以及焊接材料的差异也会影响搅拌工具的使用寿命。在实际生产应用中,若出现搅拌工具的破损或折断,将严重影响焊缝的质量与连接强度。因此,笔者在改善声发射监测方法的同时引入了小波分析法对所采集到的声发射信号进行分解,并且计算各个频率段的能量分布来寻找搅拌头工具在加工7075铝合金过程中出现严重磨损或破损时的声发射特征参数,并以此作为工具破损预测的依据。
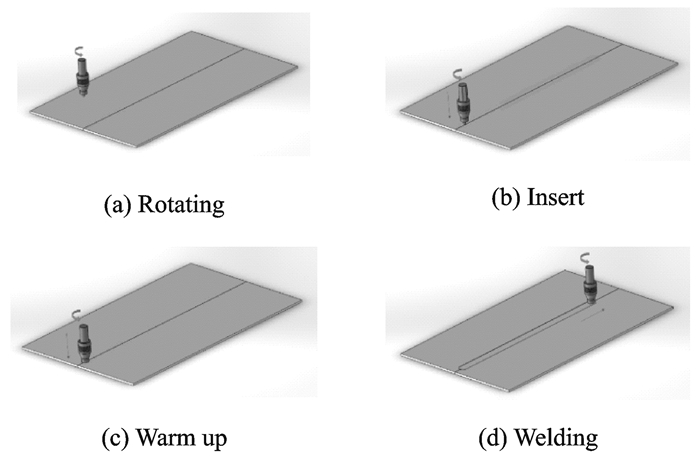
1 信号特征与信号获取搅拌摩擦连接过程可以分成以下4个部分:搅拌头工具高速旋转、搅拌头工具插入待焊接工件、搅拌头轴肩压紧工件摩擦产生热量使待焊接工件热软化、搅拌头工具沿着待焊接界面移动从而实现固相连接。图 1是搅拌摩擦焊接的过程示意图。
|
图 1 搅拌摩擦焊接过程 Figure 1 Process of friction stir welding |
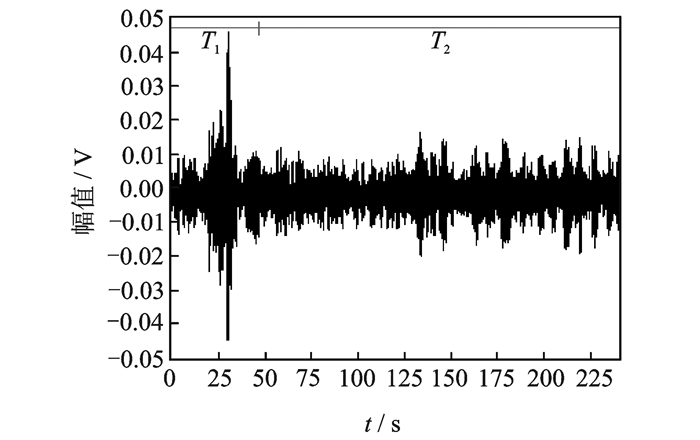
在旋转阶段,声发射信号主要来源于机床本身,信号频率处在一定范围内,属于噪音信号,可以通过在采集模块中设置滤波器来过滤掉机床噪声信号。在插入阶段,由于待焊接工件发生塑性变形而产生大量的突发型声发射信号。在预热阶段与焊接阶段,有与搅拌工具的轴肩与待焊接工件摩擦产生大量的热量使待焊接工件软化,当搅拌头工具沿着焊缝移动时,已塑化的材料从搅拌工具的前进侧移动到后退侧,并在搅拌头轴向锻造力的作用下完成金属材料的固相连接;在这一过程中,由于材料不断地发生塑性变形而产生大量连续的声发射信号。图 2是搅拌摩擦焊加工过程中声发射信号示意图,其中T1为旋转与插入阶段,T2为焊接阶段。
|
图 2 声发射信号示意图 Figure 2 Schematic of acoustic emission signal |
整个焊接过程中声发射信号特征呈现为突发型与连续性相混合的声发射信号,连续性具有幅值低、频率高的特性,突发型通常幅值较高,事件频率较低。当搅拌工具破损、折断时,释放的应力能将转化成突发型声发射信号,该信号具有上升时间短、在高频区内灵敏度较高、抗干扰能力强,同时受加工参数的影响较小等特征。
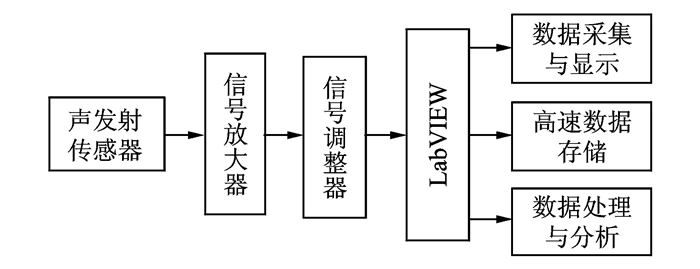
为了能精确地采集到搅拌摩擦连接过程中的声发射信号,系统所采用的数据采集卡为研华公司的PCI-1714UL,是一款基于PCI总线构架、精度高达12位的四通道高性能数据采集卡,最大可以实现10 MS/s的模拟量采集,到主机内存的A/D采样数据具有连续不间断、高速和流式的特点。同时,该类型数据采集卡支持DMA (Direct memory access)数据传输,极大地增加了数据采集卡与工控机内存之间的数据传输效率,图 3为系统的结构图。系统所选用的声发射传感器为声华公司的SR800型宽频带声发射传感器,其频带范围为50~800 kHz,具有较高的灵敏度,其配套的前置放大器为PAI型前置放大器,带宽为10 kHz~2 MHz,增益为40 d B,完全适用于搅拌摩擦焊声发射信号的在线监测。
|
图 3 数据采集系统结构图 Figure 3 Diagram of data acquisition system structure |
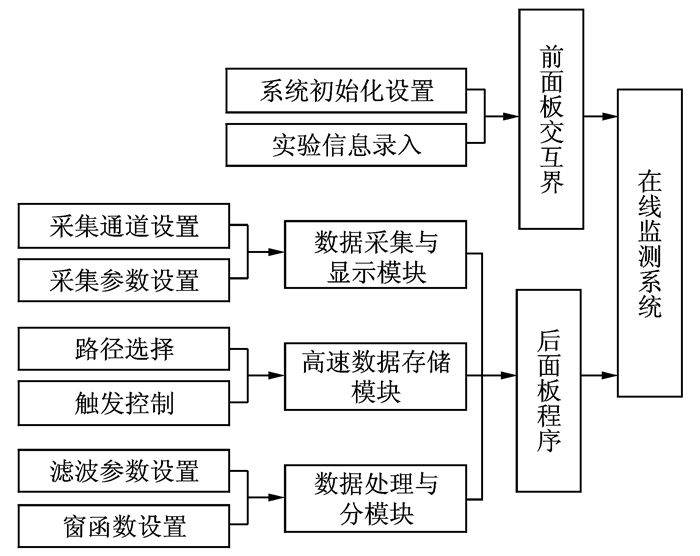
系统中的软件部分是以National Instruments公司的LabVIEW 2014作为软件的开发平台,利用该平台提供的图形化编程语言(G语言)编写而成,系统分为前面板(人机交互界面)与后面板(后台程序)两个部分。系统的后面板程序是整套软件系统的核心部分,负责系统运行时的数据转换、高速数据存储、后续数据的离线分析与处理,是前面板正常运行的重要保障。整个后面板的编写采用模块化的编程思想,主要分为数据采集与显示模块、高速数据存储模块、数据处理与分析模块。图 4表示在线监测系统软件设计流程图。
|
图 4 在线监测系统软件设计流程图 Figure 4 Flow chart of designed online monitoring system software |
2 搅拌摩擦连接实验
完成在线监测系设计与搭建后,采用赛福特公司FSW-LM-A10型号的搅拌摩擦焊设备进行焊接实验,其连接的最大厚度为16 mm,连接的长度达1 000 mm。实验中所采用的试样材料为707 5铝合金,每块板材尺寸为200 mm×100 mm×8 mm。实验中所用的搅拌头工具为自行设计的带有螺纹的搅拌针工具,螺距为1.5,材料为工具钢。
实验时,声发射传感器安装在待焊接工件上,以减少信号的衰减程度,当搅拌头与工件接触时开始数据采集;声发射传感器将所监测到的声发射信号转化为电压信号,然后经信号放大器放大后再通过信号调理器输入到数据采集卡中的数据缓冲区。最后,基于LabVIEW的声发射监测系统读取来至数据采集卡缓存中的数据并在程序的前面板中实时显示、初步处理、存储。图 5所示为实验现场图。

|
图 5 实验现场 Figure 5 Experimental scene |
在搅拌摩擦连接的过程中影响声发射变化的因素主要有主轴转数、焊接速度、下压量、工具参数、工件参数和工具磨损量等。在实验中工具参数、工件参数皆属于固定影响因素,主轴转数、焊接速度、下压量和工具磨损量为变化因素,其中工具的磨损量属于焊接过程中的不可控因素;实验的目的是为了研究搅拌工具磨损状态与声发射信号之间的映射关系,所以需要将工具磨损量转变为可控的影响因素。在实验中每焊接一块上述固定尺寸的7075铝合金,取下搅拌工具,观察并测量其磨损量,若搅拌针螺纹部分被磨钝则定义为轻微磨损,若螺纹全部破损则为严重磨损。图 6所示为搅拌头的不同磨损状态。

|
图 6 搅拌头的不同磨损状态 Figure 6 Different wearing states of stir tools |
为了获得可靠的实验数据,使实验结果具有可比性,共进行了6组实验,每组实验中分别使用参数相同的搅拌工具从新刀状态加工到搅拌针轻微磨损、严重磨损状态,并且采集全过程中的声发射信号。6组实验参数如表 1所示。
| 表 1 焊接参数 Table 1 Welding parameters |
3 信号处理与小波分析
目前对采集和处理声发射信号的方法可分为声发射信号特征参数分析法和声发射信号波形分析法两大类。特征参数分析法是一种经典的声发射信号处理方法,其原理是用多个简化的波形特征参数来表示信号的特征,然后通过对这些波形特征参数进行处理与分析来得出相应的结论。波形分析法是将声发射信号的波形存储与记录下来,通过对波形进行频谱分析,例如快速傅里叶变换、小波变换、希尔伯特黄变换等分析方法,来得出相应的信号特征。针对不同的声发射源这两种方法有着各自的优点,特征参数分析法更加简洁,波形分析法的应用更加广泛[6]。其中,波形法中运用小波分析的研究方法日渐成熟并且成为声发射信号研究领域中的研究热点[7-9]具有较强的实际应用性。
3.1 小波变换与分析理论小波分析(Wavelet analysis)是在傅里叶分析的基础上发展起来的;其核心思想是将波形函数表示为母小波(Mother wavelet)与尺度函数(Scaling function)缩放和平移后的集合。设ψ(t)满足下述容许性条件
| $ {\mathit{C}_\mathit{\psi }}{\rm{ = }}\int {\frac{{{{\left| {\mathit{\psi }\left( \mathit{\omega } \right)} \right|}^{\rm{2}}}}}{{\left| \mathit{\omega } \right|}}{\rm{d}}\mathit{\omega < }\infty } $ | (1) |
| $ {\mathit{W}_\mathit{\psi }}\mathit{f}\left( {\mathit{a}{\rm{, }}\mathit{b}} \right){\rm{ = }}{\left| \mathit{a} \right|^{\frac{1}{2}}}\int {\mathit{f}\left( \mathit{x} \right)} \overline {\mathit{\psi }\left( {\frac{{\mathit{x}{\rm{ - }}\mathit{b}}}{\mathit{a}}} \right)} {\rm{d}}\mathit{x} $ | (2) |
称为f(x)以ψ(t)为基的连续小波变换。
引入符号,将式(2)变换为
| $ {\mathit{\psi }_{\mathit{a}{\rm{, }}\mathit{b}}}\left( \mathit{x} \right){\rm{ = }}{\mathit{\psi }_\mathit{a}}\left( {\mathit{x}{\rm{ - }}\mathit{b}} \right){\rm{ = }}{\left| \mathit{a} \right|^{\frac{1}{2}}}\mathit{\psi }\left( {\frac{{\mathit{x}{\rm{ - }}\mathit{b}}}{\mathit{a}}} \right) $ | (3) |
式(3)可改写为
| $ {\mathit{W}_\mathit{\psi }}\mathit{f}\left( {\mathit{a}{\rm{, }}\mathit{b}} \right){\rm{ = }}\left\langle {\mathit{f}\left( \mathit{x} \right){\rm{, }}{\mathit{\psi }_{\mathit{a}{\rm{, }}\mathit{b}}}\left( \mathit{x} \right)} \right\rangle $ | (4) |
式中:a为伸缩因子;b为平移因子。
根据小波的定义可以看出,小波变换的同时具有时间窗和频率窗,能够在时域和频域上同时定位。这种分析方法克服了傅里叶变换的两大局限:不能刻画时域信号的局部特性、处理瞬时非平稳信号的效果差。
在对声发射信号进行分析时为了凸显高频段的细节特征,常常会将信号分解成一个低频信号和一个高频信号,并且对低频信号与高频信号继续分解下去的小波包分析。这样分析能够为信号提供更精确的分析方法,它将频带进行多层划分,对多分辨率分析没有细分的高频部分进一步分解,并能够根据信号的特征,自适应地选择响应频带,使之与信号频谱匹配,从而进一步提升分辨率。图 7为n层多分辨率小波包分解结构。

|
图 7 多分辨率小波包分解结构 Figure 7 Multiresolution wavelet packet decomposition structure |
刻度系数和小波系数可由式(5,6)得到
| $ {\mathit{d}_{\mathit{j}{\rm{ + 1, }}\mathit{k}}}{\rm{ = }}\sum\limits_{{\rm{ - }}\infty }^{{\rm{ + }}\infty } \mathit{h} \left( {\mathit{i}{\rm{ - 2}}\mathit{k}} \right){\mathit{d}_{\mathit{j}{\rm{, }}\mathit{k}}} $ | (5) |
| $ {\mathit{c}_{\mathit{j}{\rm{ + 1, }}\mathit{k}}}{\rm{ = }}\sum\limits_{{\rm{ - }}\infty }^{{\rm{ + }}\infty } \mathit{g} \left( {\mathit{i}{\rm{ - 2}}\mathit{k}} \right){\mathit{d}_{\mathit{j}{\rm{, }}\mathit{k}}} $ | (6) |
图 7中:S为时域信号;A代表完整的低频成分;D代表完整的高频成分。则原始信号为
| $ \mathit{S}{\rm{ = }}\sum\limits_{\mathit{l} = 1}^\mathit{n} {{\mathit{D}_{\mathit{k}{\rm{, }}\mathit{l}}}} {\rm{ + }}\sum\limits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {{\mathit{A}_{\mathit{k}{\rm{, }}\mathit{i}}}} $ | (7) |
原始信号的总能量为
| $ {\mathit{E}_{\mathit{f}\left( \mathit{n} \right){\rm{ = }}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^\mathit{N} {{{\left[ {{\mathit{A}_\mathit{j}}\mathit{f}\left( \mathit{n} \right)} \right]}^{\rm{2}}}} {\rm{ + }}\sum\limits_{\mathit{n}{\rm{ = 1}}}^\mathit{N} {{{\left[ {{\mathit{D}_\mathit{j}}\mathit{f}\left( \mathit{n} \right)} \right]}^{\rm{2}}}} $ | (8) |
式中:
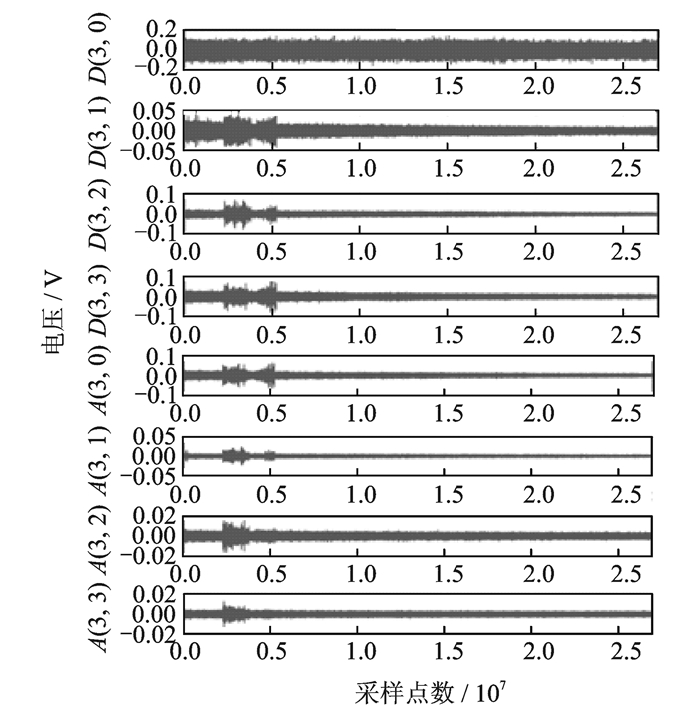
分别采集得到上述3种不同磨损程度的搅拌工具在4种工况下的声发射信号,并对信号进行3层小波包分解,采用“db4”系列小波基和“Shannon”熵标准,8个频段的子信号。图 8是新刀在第1组实验参数下的声发射信号的3层小波包分解重构图。可以看出,在信号比较平稳、持续性的突发型声发射主要来自加工过程中焊缝边缘处产生连续性飞边时,工件材料产生连续塑性变形而释放的声发射信号。图 9为新刀在第1组实验参数下各个频段小波能量占比,能量大部分集中在低频部分,随着频段增加能量占比降低。
|
图 8 新刀AE信号3层小波包分解 Figure 8 Three-layer wavelet packet decomposition of AE signal for new tool |

|
图 9 新刀AE信号各频段能量 Figure 9 Energy of each frequency band of AE signal for new tool |
图 10所示为在第1组实验参数下搅拌工具出现轻微磨损时声发射信号的3层小波包分解重构。从图中可以看出,高频部分的A(3, 3)频段出现较大的波动且持续时间较短,属于突发型声发射,符合工具磨损时所产生的声发射信号类型。在D(3, 1), D(3, 2), D(3, 3)与A(3, 0)频段中出现持续时间较长的突发型声发射,是由于加工过程中焊缝边缘处产生连续性飞边而引起的。

|
图 10 工具轻微磨损AE信号3层小波包分解 Figure 10 Three-layer wavelet packet decomposition of AE signal for slight worn tool |
图 11为该实验条件下各个频段的能量所占比例。可以看出,第8段对应图 8中A(3, 3)有着明显的增加,高频细节更加突出。由于机床干扰,低频能量始终占据大部分,在正常情况下各部分的能量占比应处于下降趋势,当焊缝出现飞边时能量会出现一定的波动,对应图中D(3, 3)频段。

|
图 11 工具轻微磨损AE信号各频段能量 Figure 11 Energy of each frequency band of AE signal for slight worn tool |
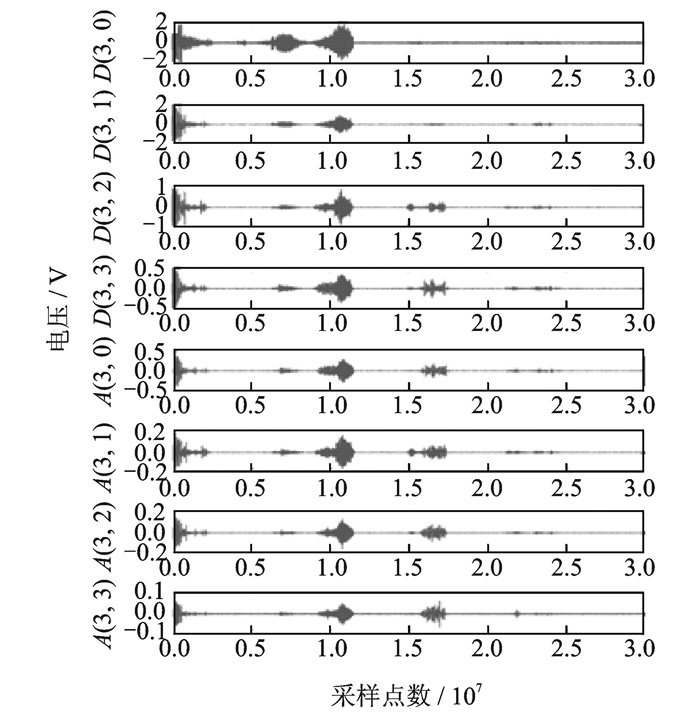
图 12为工具严重磨损时的AE信号小波包分解重构。从图中可以看出,工具严重磨损时高频段的振幅相比轻微磨损提高了10倍,并且所持续的时间有所增加,这是由于搅拌工具发生连续性磨损并不断释放出大量声发射信号。由高频部分的小波变化可知,工具连续磨损的声发射信号频率明显高于工件发生塑性变形时所发出的声发射信号。
|
图 12 工具严重磨损AE信号3层小波包分解 Figure 12 Three-layer wavelet packet decomposition of AE signal for severe worn tool |
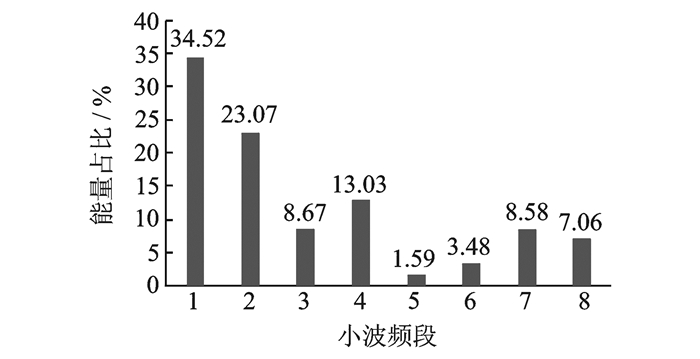
图 13为该条件下各频段能量所占比例,低频部分所占比例急剧下降,A(3, 2)与A(3, 3)频段相比轻微磨损增加十余倍,高频段能量占比呈上升趋势。这些信号与能量的变化可以作为工具磨损的特征参数。
|
图 13 工具严重磨损AE信号各频段能量 Figure 13 Energy of each frequency band of AE signal for severe worn tool |
为了能说明该结论的正确性,用相同的方法分析了在全部参数下的实验结果,所得结论基本一致。结果如图 14所示。

|
图 14 6组实验参数下各个频段能量变化趋势 Figure 14 Energy trends of each frequency band of six groups of experimental parameters |
4 结论
本文基于声发射技术设计并搭建了一套在线监测系统,对不同磨损状态的搅拌头工具在不同的工艺参数条件下进行了在线监测的数据采集实验。对采集的数据进行小波包分解,得到了不同磨损状态下的各频段能量分布关系。主要结论如下:
(1) 在搅拌摩擦焊接的不同阶段,具有不同的声发射信号特征,插入阶段具有高幅值突发型特征,稳态焊接阶段具有低幅值、高频率特征。
(2) 小波包分解表明,不同磨损状态的搅拌头工具具有明显不同的各频段能量占比。新刀的低频段能量占比最高,随着搅拌头工具磨损的增加,低频段能量占比明显降低。
(3) 不同工艺参数条件下不同磨损状态的搅拌头的小波包分解表明,各频段能量占比均具有相同的变化趋势,随着搅拌头的磨损加剧,低频段能量占比减小,高频段能量占比增加。由此表明,可以通过声发射在线监测技术来监测搅拌摩擦焊接过程中搅拌头的磨损情况。
| [1] |
RAJASHEKAR R, RAJAPRAKASH B M.
Development of a model for friction stir weld quality assessment using machine vision and acoustic emission techniques[J]. Journal of Materials Processing Tech, 2016, 229(33): 265–274.
|
| [2] |
陈高强, 史清宇.
搅拌摩擦焊中材料流动行为数值模拟的研究进展[J]. 机械工程学报, 2015, 51(22): 11–21.
CHEN Gaoqiang, SHI Qingyu. Research progress of numerical simulation of material flow in friction stir welding[J]. Chinese Journal of Mechanical Engineering, 2015, 51(22): 11–21. |
| [3] |
SUBRAMANIAM S K, NARAYANAN S, ASHOK S D.
Acoustic emission-based monitoring approach for friction stir welding of aluminum alloy AA6063-T6 with different tool pin profiles[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2013, 227(227): 407–416.
|
| [4] |
SOUNDARARAJAN V, ATHARIFAR H, KOVACEVIC R.
Monitoring and processing the acoustic emission signals from the friction-stir-welding process[J]. Proceedings of the Institution of Mechanical Engineers Part B:Journal of Engineering Manufacture, 2006, 220(10): 1673–1685.
DOI:10.1243/09544054JEM586
|
| [5] |
SURESHA C N, RAJAPRAKASH B M, UPADHYA S.
Applicability of acoustic emission in the analysis of friction stir welded joints[J]. International Journal of Recent Trends in Engineering, 2009(1): 86–89.
|
| [6] |
沈功田, 耿荣生, 刘时风.
声发射信号的参数分析方法[J]. 无损检测, 2002, 24(2): 72–77.
SHEN Gongtian, GENG Rongsheng, LIU Shifeng. A parametric analysis method of acoustic emission signal[J]. Nondestructive Testing, 2002, 24(2): 72–77. |
| [7] |
纪洪广, 张天森, 张志勇, 等.
无损检测中常用声发射参数的分析与评价[J]. 无损检测, 2001, 23(7): 289–291.
JI Hongguang, ZHANG Tiansen, ZHANG Zhiyong, et al. Analysis and evaluation of commonly used acoustic emission parameters in nondestructive testing[J]. Nonde Structive Testing, 2001, 23(7): 289–291. |
| [8] |
GENG R S, SHEN G T, LIU S F.
A study on modal acoustic emission theory[J]. Nonde Structive Testing, 2002, 24(7): 302–306.
|
| [9] |
焦敬品, 何存富, 吴斌, 等.
基于模态分析和小波变换的声发射源定位新算法研究[J]. 仪器仪表学报, 2005, 26(5): 482–485.
JIAO Jingpin, HE Cunfu, WU Bin, et al. A new algorithm for acoustic emission source localization based on modal analysis and wavelet transform[J]. Chinese Journal of Scientific Instrument, 2005, 26(5): 482–485. |
| [10] |
郑治真.
小波变换及其MATLAB工具的应用[M]. 北京: 地震出版社, 2001: 47-55.
ZHENG Zhizhen. Wavelet transform and its MATLAB tools[M]. Beijing: Earthquake Press, 2001: 47-55. |
| [11] |
CHEN C, KOVACEVIC R, JANDGRIC D.
Wavelet transform analysis of acoustic emission in monitoring friction stir welding of 6061 aluminum[J]. International Journal of Machine Tools & Manufacture, 2003, 43(13): 1383–1390.
|
| [12] |
周伟.
MATLAB小波分析高级技术[M]. 西安: 西安电子科技大学出版社, 2006: 14-20.
ZHOU Wei. Advanced MATLAB wavelet analysis[M]. Xi'an: Xidian University Press, 2006: 14-20. |
| [13] |
CHEN C H, JIANN-DER L, LIN M C.
Classification of underwater signals using wavelet transforms and neural networks[J]. Mathematical & Computer Modelling, 1998, 27(2): 47–60.
|
 2018, Vol. 50
2018, Vol. 50


