虽然研究人员很早就意识到对多级涡轮内部的非定常性及其影响的研究可能具有深远意义,但是在试验台上对多级涡轮进行非定常测量的难度大、费用高,而进行多级涡轮内部非定常流动数值仿真对计算资源的需求量也极大,因此对涡轮内部非定常流动现象的研究进展一直很缓慢,认识水平也较为有限。直至20世纪90年代,随着试验测试能力的提高以及数值仿真技术的发展,越来越多的研究者开始关注多级涡轮内部的非定常流动,并取得了许多重要的研究成果。
现有的研究指出,静止叶排周向相对位置关系将决定上游尾迹进入下游叶栅通道的相位,从而改变下游叶栅通道内的流场,并最终影响多级涡轮的气动性能,即所谓的时序效应(Clocking effect)。Huber等[1]针对三级低压涡轮的相邻两排静叶时序位置开展了试验研究,研究结果表明在不同的时序位置处涡轮气动效率波动范围为±0.5%左右。Griffin等[2]在此基础上通过数值仿真的方法对该三级低压涡轮的最佳时序位置进行了分析和预测,证明了通过计算流体力学的方法预测涡轮的最佳时序位置的可行性。随着对转静干涉现象研究的不断深入,Dorney和Cizmas等[3, 4]发现当上游叶片的尾迹对准下游叶片前缘时效率最高,而当上游叶片的尾迹从下游叶片通道中间流过时效率最低,这一结论也被后续开展的一系列试验和数值仿真研究[5-7]所证实。鉴于数值仿真的手段在获取局部流场信息、节约试验成本方面的显著优势,研究人员针对叶轮机的时序效应开展了一系列数值研究。石、邓清华等[8]对Aachen一级半轴流式透平进行了全三维非定常有黏流动数值模拟,并通过对相邻叶排间干涉现象的分析阐述了时序效应产生的原因。李红丽等[9]通过ANSYS CFX对某单级跨声速涡轮进行了数值研究,研究结果表明不同时序位置下的涡轮等熵效率差异最大可以达到1.2%。
然而并不是所有的时序设计都取得了明显的性能收益,Evans等[10]对某双级低压涡轮的试验研究结果表明在不同的时序位置下,其效率收益只有不到0.2%。Behr等[11]对某双级小展弦比涡轮的时序研究分析结果表明在叶片不同径向高度处的最佳时序相位不同,简单地改变下游叶片的时序位置带来的涡轮整体效率变化只有±0.15%。陈江、季路成等[12]详细分析了最佳时序相位的径向分布特征,并提出了“缘线匹配”的设计方法,缘线匹配设计前后的数值仿真结果对比表明,通过缘线匹配可以进一步提升涡轮气动性能。除了最佳时序位置的径向分布差异以外,叶片数的比例也是影响时序设计效果的重要因素。李伟等[13]对某1+1/2级涡轮开展了数值仿真研究,相邻两级涡轮静叶的叶片数分别为84和126,其比值为2:3,研究结果表明不同时序位置处的涡轮效率差异仅为0.1%。Jerzy等[14]进一步分析了这一现象出现的原因并得出结论,只有当设计对象的叶片数相等时才能获得较为明显的时序设计收益。
但是上述研究即便是针对高压涡轮也均未考虑冷气对主流流动的影响。在有冷气的条件下,由于冷气的总压通常高于主流而温度则低于主流,因此在冷气与主流掺混的情况下尾迹高损失区已经不再具有低总压、高熵的特征。此外,在上游尾迹的作用下,不同时序位置下的第2级静叶表面的静压分布也呈现出了一定差异,静压分布的变化影响了第2级静叶表面冷气的出流流量,进而对涡轮性能产生了影响。当冷气进入主流时,在壁面法向动量差异产生的剪切作用下,在射流前缘附近形成湍流度极高的“涡卷”,涡卷向射流下游延伸并最终与叶片尾缘处的脱落涡混合,形成明显的高涡量区,即气冷叶片的尾迹区。
本文针对某型涡扇发动机双级高压涡轮静叶时序效应开展了非定常计算,并针对不同时序位置下的高压涡轮气动性能进行了分析。本研究采用成熟商业软件NUMECA中的AutoGrid5模块进行网格生成,并运用结构化网格对叶身气膜孔进行了精细化模拟,最终采用ANSYS CFX对算例进行前处理、求解计算和后处理。
1 物理模型和计算方法 1.1 研究对象本文的研究对象为双级轴流亚声速气冷高压涡轮,冷气总流量占高压涡轮进口物理流量的30%以上。该型高压涡轮在设计之初即考虑后续开展时序设计优化的可能性,并在叶片数选取时有针对性地将第1级和第2级静叶的数目选取为相同的数值。计算采用几何约化[15]的方法,为保证时序设计的有效性,静叶的叶型及叶片数并未进行调整,仅对动叶叶片进行约化,4排叶片的叶片数比例为2:3:2:4,这种处理方法能够考虑到转静叶片之间互相干涉的影响,在工程中也得到了广泛应用(Rai[16],Clark[17],Arnone [18])。约化前后的叶形如图 1所示。

|
图 1 叶形约化与时序位置示意图 Figure 1 Airfoil scaling and clocking position |
本研究将对一级静叶1个节距内的6个时序位置进行考察,CP-N(周向偏移量等于N-1乘以节距)分别等于0.0,0.2,0.4,0.6,0.8和1.0,其中基准位置(CP-1)定义为第1级静叶(以下简称一静)的积叠轴相对第2级静叶(以下简称二静)的积叠轴顺航向逆时针旋转4.78°时的位置。然后将一级静叶沿顺航向顺时针旋转,可依次得到其余时序位置。为尽可能使二级静叶出口边界条件接近真实情况,本计算对双级涡轮的全部4排叶片进行了数值模拟。
1.2 边界条件计算采用均匀进口总压边界条件,进口温度边界条件为考虑径向温度分布的温度函数,在涡轮出口采用压力出口边界条件。各排叶片及上、下缘板固体壁面选取无滑移绝热边界条件。叶身各气膜孔边界条件指定为自由流动边界(Opening)并按照涡轮叶片内流设计结果给定气膜孔的进口温度、压力、速度矢量和湍流度。转静交界面采用滑移平面法进行处理。
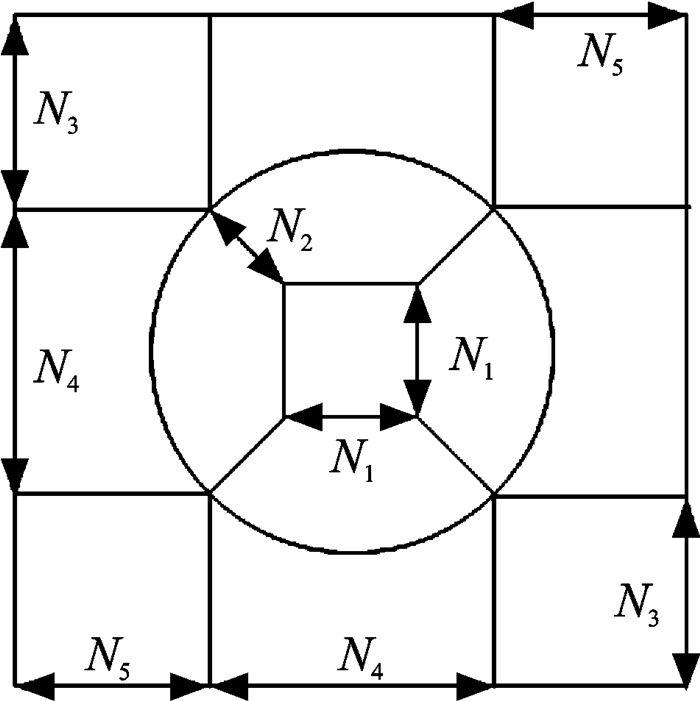
1.3 网格划分本分析采用NUMECA中的自动网格生成模块AutoGrid5进行网格生成,选取AutoGrid5中的默认网格拓扑结构,叶形周围采用O形贴体网格,其余位置采用H形分块结构化网格。网格生成过程中还对尾缘附近的网格进行了加密,并通过调整首层网格厚度的方法使壁面“Y+值”小于1。考虑到定常计算过程中惯常采用的冷气喷射源项法[19]需要指定冷气流量,无法准确反映下游叶片在上游尾迹扫掠下表面静压变化所带来的冷气流量的周期性脉动,因此本分析采用结构化网格对各叶片排叶身的气膜冷却孔进行了详细模拟,冷气孔采用蝶形网格,其拓扑结构如图 2所示,带气膜冷却的第1级静叶网格如图 3所示。
|
图 2 冷气拓扑结构示意图 Figure 2 Topology of cooling hole internal mesh |

|
图 3 非定常计算网格示意图 Figure 3 Sample of mesh used for unsteady simulation |
为了验证计算所用网格合理性,在定常计算条件下分别针对叶片和气膜孔进行了网格无关性分析。表 1给出了不同叶栅网格量(不考虑冷气域)下的涡轮流量、功率和效率等参数计算结果,发现当单排网格数达到50万时,涡轮各性能参数变化已不再显著,可认为该网格数已满足无关性要求。
| 表 1 涡轮性能的网格无关性 Table 1 Mesh-independence of turbine performance |
以单排50万网格的叶栅为基准,在分析时令N1=N2=N3=N4=N5=Nm,表 2给出了不同单孔网格数下以Nm=5为基准的相对冷气流量。分析结果表明当Nm≥13时计算结果变化较小。但为了降低非定常计算量,本计算中取Nm=9,此时冷气流量相比Nm=17偏低0.07%,该流量偏差与高压涡轮进口物理流量之比小于0.03%,不会显著影响计算结果。
| 表 2 气膜孔流量网格无关性 Table 2 Mesh-independence of cooling hole mass flow |
1.4 求解模型
本研究采用ANSYS CFX求解三维有黏的雷诺平均Navier-Stokes方程组,湍流模型选取剪切压力传输(Shear stress transport,SST)模型以封闭方程组,相比于单方程的S-A模型以及双方程的k-ε,k-ω模型,SST模型通过对涡粘性系数公式的修正解决了湍流剪切应力输运问题,显著提高了逆压梯度条件下流动分离状况的预测精度,在许多验证性研究工作中已经得到证实[20]。
2 结果分析 2.1 时序位置对涡轮总性能的影响在本分析中高压涡轮效率使用美国通用电气公司(General electric company,GE)对气冷涡轮的两种效率定义方式分别进行统计,其中41截面效率定义见式(1),热效率定义见式(2),则
| $ {{\mathit{\eta }}_{\text{41}}}\text{=}\frac{ \Delta \mathit{H}}{{{\mathit{W}}_{\text{41}}} \cdot \Delta {{\mathit{h}}_{\text{41}}}} $ | (1) |
| $ {{\mathit{\eta }}_{\text{thermal}}}\text{=}\frac{ \Delta \mathit{H}}{{{\mathit{W}}_{\text{40}}} \cdot \Delta {{\mathit{h}}_{\text{40}}}\text{+}\sum{\text{(}{{\mathit{W}}_{\mathit{c}}} \cdot \Delta {{\mathit{h}}_{\mathit{c}}}\text{)}}} $ | (2) |
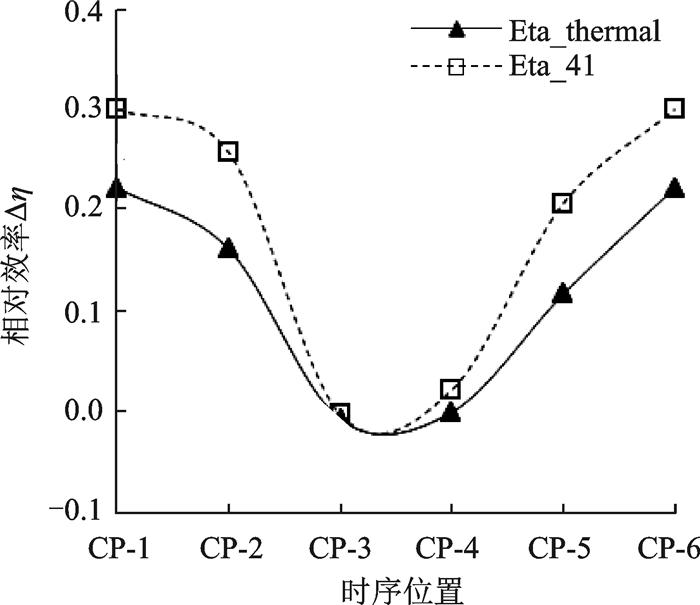
式中:W40为涡轮进口流量;W41为涡轮一级静叶出口流量; Wc为各股冷气出口流量; Δh40为从涡轮进口到涡轮出口的等熵膨胀功; Δh41为从一静出口到涡轮出口的等熵膨胀功; Δhc为从气膜孔出口到涡轮出口的等熵膨胀功; ΔH为涡轮输出的流道功。不同时序位置下非定场计算得到的涡轮效率与定常计算得到的涡轮效率之间的差异Δη如图 4所示。从图 4可以看出,不同时序位置下涡轮41截面效率的差异可以达到0.33%,而热效率差异仅有0.26%。值得注意的是,两种效率随时序位置的变化趋势相同,仅有波动幅值存在差异。
|
图 4 不同时序位置下的涡轮效率 Figure 4 Turbine efficiency variation on clocking positions |
表 3为不同时序位置下各叶排冷气流量与定常计算结果中对应叶排冷气流量的相对量,从表 3可以看出,时序位置对整个第2级冷气质量流量的影响均较为显著,在效率最高的时序位置(CP-1)比效率最低的时序位置(CP-3)对应的二级静叶冷气出口质量流量高出15.6%。
| 表 3 不同时序位置各叶排冷气相对质量流量 Table 3 Relative cooling mass variation for each row at different clocking positions |
为进一步分析冷气流量出现差异的位置,表 4展示了不同时序位置下2级静叶/动叶前尾缘处的冷气量(2级静叶/动叶压力面和吸力面侧均无气膜冷却)。不难发现时序位置对尾缘冷气量的影响要远小于对前缘冷气量的影响,这也说明上游尾迹传递过程中造成的叶排进口压力分布差异是造成冷气量差异的主要原因。而尾缘劈缝位置的冷气流量主要受叶栅喉部马赫数的影响,因此在不同时序位置处变化较小。
| 表 4 不同时序位置第2级静叶/动叶冷气流量 Table 4 Cooling mass of 2nd vane and 2nd rotor at different clocking positions |
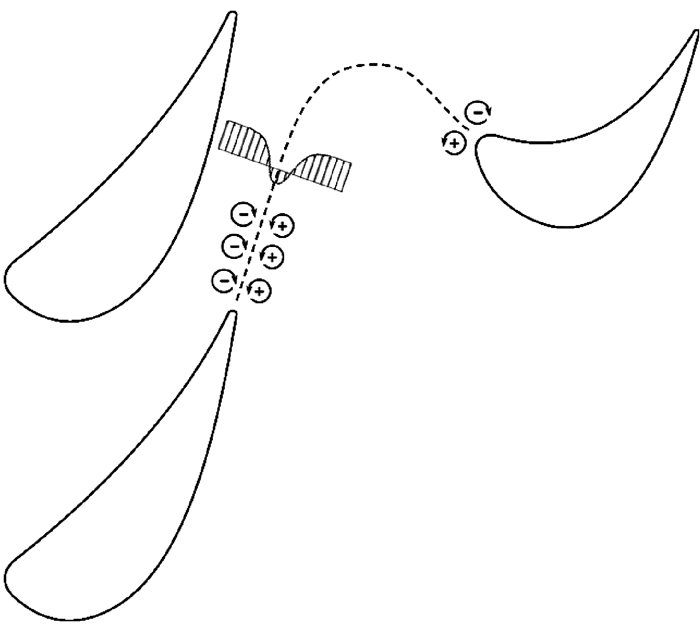
由于表面粘性的存在,上游叶排的尾迹通常具有速度亏损的特征,因而可以视为相对主流区域具有反向速度的射流,即“逆射流”[21]。如图 5所示。在叶片的压力面和吸力面侧形成一组对涡,这组对涡在动叶叶栅通道内发生偏转,并传递至下游静叶前缘。当对涡的中心正对二级静叶前缘时,这种速度亏损将使得前缘气膜冷却出口流速增加,冷气流量增大;而当尾迹从二级静叶之间通过时,二级静叶前缘冷气量相对较小。
|
图 5 尾迹的“逆射流”效应 Figure 5 Negative jets effect at trailing edges |
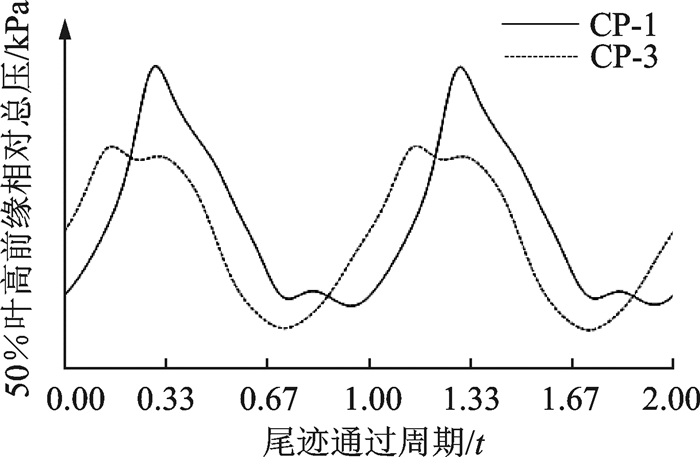
不同时序位置下二级静叶叶型损失的差异客观上导致了二级动叶进口相对总压的差异。在效率最高的时序位置CP-1,二级静叶出口静压最高,因此二级动叶前缘气膜孔两侧压差减小,冷气量降低,如图 6所示。在所统计的通道周期内,时序位置CP-1对应的二级动叶进口相对总压要整体高于CP-3所对应的二级动叶进口相对总压。
|
图 6 不同时刻二级动叶进口相对总压 Figure 6 Time-varied relative pressure at the second vane inlet |
由于41截面效率定义中的理想功部分忽略了一静出口以后的冷气做功,当41截面流量不变时理想焓降不变,而二静冷气量降低将直接导致实际做功流体的减少,因此涡轮流道功减少、效率下降。对于涡轮热效率而言,当冷气量减小时,涡轮热效率理论上应有所提高[22]。但是从图 4可以看出,当涡轮处于总冷气量最小的时序位置CP-3时,其热效率也最低。目前主流的看法是不同的时序位置处上游叶片尾迹会对下游叶片的附面层及分离泡产生不同的影响。当上游尾迹冲击在下游叶片前缘时,具有高湍流度特征的流体与下游叶片表面的附面层掺混,对吸力面分离起到一定抑制作用。本算例中,冷气量最小的位置对应的涡轮效率也最低,这也从另一方面证明了不同时序位置处冷气量的差异并不是导致涡轮效率的主要因素。
2.2 时序位置对涡轮流场的影响在此前不考虑冷气掺混的涡轮时序效应研究工作中,通常采用熵分布对上游叶片尾迹输运过程进行追踪和展示(李昂[23],李伟[24])。但是考虑到叶身冷气对主流的影响之后,由于冷气的温度显著低于主流,熵值较低,因此一静的尾迹在叶身气膜冷气的掺混作用下并没有像无冷气涡轮一样呈现出高熵值的特征,而是形成了一个明显的低熵值区域。图 7为一静出口和二静进口的时均熵分布云图。一静的尾迹在流经一动叶栅的过程中与主流发生掺混,熵值逐渐增加,至二静进口时已经无法被清楚地辨别出来。

|
图 7 一静出口和二静进口时均熵分布 Figure 7 Time-averaged static entropy distribution of 1st vane outlet and 2nd vane inlet |
为更为清晰地观察一静尾迹向下游的输运过程,本研究利用涡量分布来监控尾迹的输运过程。燃气流经叶栅通道以后,会在尾迹区域形成一个由通道涡、尾缘涡以及尾缘区域展向涡组成的集中涡系。杨彤等[25]的研究表明,上游静叶集中涡系对下游叶片表面附面层存在显著影响,进而使得下游叶栅通道涡的强度和范围都发生了显著变化。而冷气射流使得吸力边和压力边附近出现明显的多射流卵形涡系[26],随距喷射点距离的增加,射流涡逐渐变得均匀。效率最高(CP-1)和效率最低(CP-3)两个时序位置50%截面时均涡量分布如图 8所示。
|
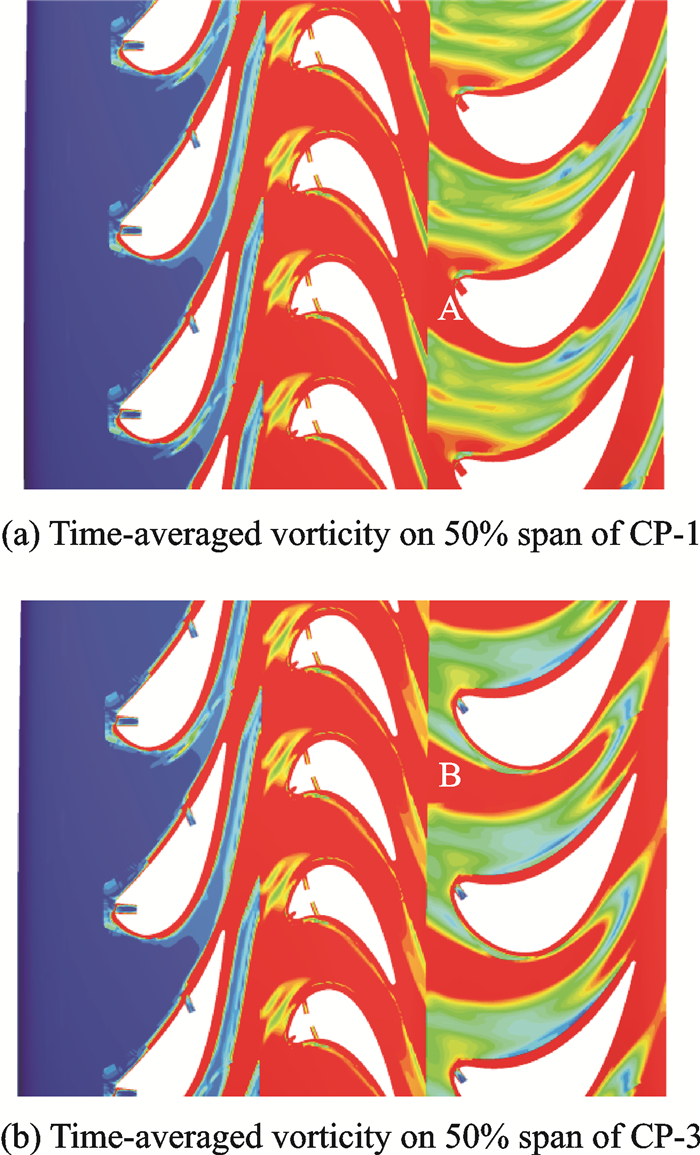
图 8 效率最高/低时序位置50%截面时均涡量分布 Figure 8 50% span time-averaged vorticity at clocking positions of maximum/minimum efficiency |
当上游尾迹造成的低能流体(高涡量区A)冲击在下游叶片前缘时效率最高;而当低能流体(高涡量区B)穿过下游叶栅通道时效率最低。图 9为效率最高的时序位置CP-1和效率最低的时序位置CP-3在10%,50%,90%叶高处二静进口时均涡量的周向分布。受到上、下端区二次流动的影响,图中10%截面和90%截面的高涡量区已经不仅仅是由于上游尾迹造成的,而是一静尾迹与上、下通道涡综合作用的结果,因此10%和90%截面的时均涡量周向分布也呈现出了显著的“多峰”特征。

|
图 9 二静进口各截面时均涡量周向分布 Figure 9 Circumferential distribution of time-averaged vorticity at 2nd vane inlet |
效率最高的时序位置和效率最低的时序位置二静时均总压损失系数如图 10所示。高压涡轮静叶端区二次流动通常较为复杂,但仍能观察发现当一静处于效率最高的时序位置CP-1时,二静叶根区域总压损失有所降低;对于叶中截面,如前文所述,当上游尾迹冲击在叶片前缘时叶栅损失最小;而对于叶尖截面,在上端区二次流动的影响下高涡量区域恰好处于通道中间,叶栅损失反而有所升高,后续仍存在优化空间。

|
图 10 二静叶栅总压损失系数径向分布 Figure 10 Radial distribution of 2nd vane total pressure loss |
3 结论
本文通过非定场数值模拟方法研究了气冷涡轮第1级静叶周向位置变化对涡轮气动性能的影响并得到以下结论:
(1) 通过时序设计可以提高气冷涡轮性能,第1级静叶不同时序位置下涡轮41截面效率差异最高可达0.33%,热效率差异为0.26%。
(2) 时序位置对叶身冷气量存在一定影响,进而对涡轮41截面效率产生影响,但冷气量变化并不是影响涡轮效率的主要因素。
(3) 考虑冷气时,通过时均熵分布已经无法准确判断上游尾迹与下游叶片前缘之间的相对位置关系。
(4) 当第1级静叶尾迹从第2级静叶叶栅通道中间流过时,下游叶栅损失增加;当第1级静叶尾迹与端区二次流造成的低能流体冲击第2级静叶前缘时,下游叶栅损失减小。
(5) 受到端区复杂二次流动的影响,最佳时序位置处第2级静叶上端区附近损失仍较高,存在优化改进空间。
| [1] |
HUBER F W, JOHNSON P D, SHARMA O P, et al. Performance improvement through indexing of turbine airfoils: Part 1-experimental investigation: ASME 95-GT-028[R]. [S. l.]: [s. n.], 1995: 1-8. |
| [2] |
GRIFFIN L W, HUBER F M, SHARMA O P.
Performance improvement through indexing turbine airfoils:Part 2-numerical simulation[J]. ASME, Journal of Turbomachinery, 1995, 118(4): 636–642.
|
| [3] |
DORNEY D J, SHARMA O P.
A study of turbine performance increases through airfoil clocking[J]. International Journal of Turbo and Jet Engines, 1998, 15(2): 119–128.
|
| [4] |
CIZMAS P, DONEY D J. Parallel computation of turbine blade clocking[C]//34th AIAA/ASME/SAE Joint Propulsion Conference. Cleveland, OH: AIAA, 1998: 13-15. |
| [5] |
JOUINI D B, BANCALARI D E. Experimental investigation of airfoil wake clocking impacts on aerodynamic performance in a two stage turbine test rig: ASME, GT2003-38872[R]. [S. l.]: [s. n.], 2003: 1-8. |
| [6] |
JING Ren, MICHAEL S, DIETER B.
Influence of stator clocking on the unsteady three-dimensional flow in a two-stage turbine[J]. Journal of Turbomachinery, 2005, 127(1): 156–163.
DOI:10.1115/1.1812780
|
| [7] |
KANG J S. Experimental investigation of nozzle vane clocking in a 2-stage low pressure turbine: ASME GT2014-25604[R]. [S. l.]: [s. n.], 2014: 1-9. |
| [8] |
石, 邓清华, 李军, 等.
一级半轴流式透平的非定常流动干涉与时序效应[J]. 动力工程, 2009, 29(2): 111–116.
SHI Yan, DENG Qinghua, LI Jun, et al. Interaction and clocking effect of unsteady flow in a one and a half axial-flow turbine stage[J]. Journal of Power Engineering, 2009, 29(2): 111–116. |
| [9] |
李红丽, 乔渭阳.
静叶时序对高压涡轮性能影响的数值研究[J]. 科学技术与工程, 2012, 12(17): 4221–4225.
DOI:10.3969/j.issn.1671-1815.2012.17.036 LI Hongli, QIAO Weiyang. A numerical investigation of stator clocking on hign pressure turbine's performance[J]. Science Techonology and Engineering, 2012, 12(17): 4221–4225. DOI:10.3969/j.issn.1671-1815.2012.17.036 |
| [10] |
EVANS K R, LONGLEY J P. Clocking in low-pressure turbine: ASME GT2016-56668[R]. [S. l.]: [s. n.], 2016: 1-17. |
| [11] |
BEHR T, PORRECA L, MOKULYS T, et al.
Multistage aspects and unsteady effects of stator and rotor clocking in an axial turbine with low aspect ratio blading[J]. ASME Journal of Turbo-machinery, 2006, 128(1): 11–22.
DOI:10.1115/1.2101855
|
| [12] |
陈江, 季路成, 杨春信.
叶轮机非定常气动设计的缘线匹配技术[J]. 航空动力学报, 2003, 18(5): 609–615.
CHEN Jiang, JI Lucheng, YANG Chunxin. Edge-matching technique for unsteady aerodynamic design of turbomachinery[J]. Journal of Aerospace Power, 2003, 18(5): 609–615. |
| [13] |
LI Wei, ZHU Xiaocheng, OUYANG Hua, et al.
Numerical simulation of clocking effect on blade unsteady aerodynamic force in axial turbine[J]. Journal of Thermal Science, 2012, 21(5): 474–482.
DOI:10.1007/s11630-012-0571-0
|
| [14] |
JERZY S.
Clocking in turbines:Remarks on physical nature and geometric requirements[J]. Polish Maritime Research, 2015, 22(2): 62–70.
|
| [15] |
RAI M M.
Three-dimensional navier-stokes simulations of turbine rotor-stator interaction. Part 1-Methodology[J]. AIAA, Journal of Propulsion and Power, 1989, 5(3): 305–311.
DOI:10.2514/3.23154
|
| [16] |
RAI M M, MADAVAN N K.
Multi-airfoil Navier-Stokes simulations of turbine rotor-stator interaction[J]. ASME, Journal of Turbomachinery, 1990, 112(5): 377–396.
|
| [17] |
CLARK J P, STETSON G M, MAGGE S S, et al. The effect of airfoil scaling on the predicted unsteady loading on the blade of a 1 and 1/2 stage transonic turbine and a comparison with experimental results: ASME 2000-GT-0446[R]. [S. l.]: [s. n.], 2000: 1-9. |
| [18] |
ARNONE A, PACCIANI R.
Rotor-stator interaction analysis using the navier-stokes equations and a multigrid method[J]. ASME, Journal of Turbomachinery, 1996, 118(4): 679–690.
DOI:10.1115/1.2840923
|
| [19] |
曾军, 唐洪飞.
气膜冷却涡轮数值仿真技术进展[J]. 航空科学技术, 2015, 26(2): 1–9.
ZENG Jun, TANG Hongfei. Progress of film-cooling turbine numerical simulation technology[J]. Aeronautical Science & Technology, 2015, 26(2): 1–9. |
| [20] |
BARDINA J E, HUANG P G, COAKLEY T J. Turbulence modeling validation: AIAA-97-2121[R]. USA: AIAA, 1997. |
| [21] |
TIMKO L P. Energy efficient engine high pressure turbine component test performance report: NASA CR-168289[R]. USA: NASA, 1990. |
| [22] |
MEYER R X.
The effects of wakes on the transient pressure and velocity distributions in turbomachines[J]. Journal of Basic Engineering, 1958, 80(7): 1544–1552.
|
| [23] |
李昂, 薛伟鹏, 葛宁.
两级高压涡轮三维时序效应研究[J]. 燃气涡轮试验与研究, 2014, 27(4): 12–17.
LI Ang, XUE Weipeng, GE Ning. 3D-clocking effect on two-stage high pressure turbine[J]. Gas Turbine Experiment and Research, 2014, 27(4): 12–17. |
| [24] |
李伟, 竺晓程, 王惠斌, 等.
时序效应对涡轮尾迹传递过程影响数值研究[J]. 推进技术, 2011, 32(4): 471–478.
LI Wei, ZHU Xiaocheng, WANG Huibin, et al. Numerical simulation of clocking effect on turbine wake transportation process[J]. Journal of Propulsion Technology, 2011, 32(4): 471–478. |
| [25] |
杨彤, 冯国泰.
动静干涉下涡轮叶栅内部涡系结构分析[J]. 汽轮机技术, 2013, 55(5): 321–325.
YANG Tong, FENG Guotai. Study of vortex system on rotor/stator interaction in HP turbine casecades[J]. Turbine Technology, 2013, 55(5): 321–325. |
| [26] |
陈浮, 冯国泰.
气冷涡轮叶栅流场结构的实验研究[J]. 哈尔滨工业大学学报, 1999, 31(1): 32–34.
CHEN Fu, FENG Guotai. Experimental study on flow field structure for cooled turbine cascade[J]. Journal of Harbin Institute of Technology, 1999, 31(1): 32–34. |
 2018, Vol. 50
2018, Vol. 50


