2. 北京空间飞行器总体设计部, 北京, 100094
2. Beijing Institute of Spacecraft System Engineering, Beijing, 100094, China
太空垃圾的增多和航天商业化的迅速发展使各航天大国越来越注重空间在轨服务技术的研究[1]。空间在轨服务技术可以完成太空垃圾的清理工作,降低空间飞行器被碰撞概率;实现在轨航天器的零部件维护、推进剂加注、辅助航天器入轨和离轨甚至在轨零件装配工作、增加飞行器在轨工作时间[2]以及未来深空探测有效载荷的锁释[3]。因此空间在轨服务成为极具研究价值和发展前景的空间技术[4-6],而重复锁紧与分离装置作为空间在轨服务技术的关键组成部分[7],其工作性能对空间在轨服务系统整体工作性能具有重要影响。
20世纪七、八十年代,相关研究人员便开始研究空间在轨服务技术[7],到目前为止,已经完成了大量的地面、空间试验和在轨应用,获得了一系列的研究成果[8],如20世纪80年代欧洲航空局设计的空间低冲击重复锁紧与分离装置,德国宇航中心1994年开展的试验服务卫星计划ESS[9] (Experimental servicing satellite,ESS), 日本宇航局于1997年11月发射工程试验卫星ETS-Ⅶ[10](Engineering test satellite-7,ETS-Ⅶ)轨道锁紧与分离维护飞行器,完成在轨合作目标的捕获与分离试验, 美国于1999年提出较为完善的在轨服务演示计划——轨道快车计划,项目于2007年完成轨道实验[11]。目前国外对于合作目标的重复锁紧与分离技术的研究已经十分成熟,成功研制出了多种经过空间在轨验证的可靠装置,国内在该领域内的研究也取得了一定的研究成果,但目前处于起步阶段。
本文针对中国未来空间在轨服务技术,提出一种针对合作目标的重复锁紧与分离方案。为保证合作目标在空间机械臂的协助下能够被捕获,对方案的容差性能进行了理论分析,在此基础上进行仿真校验和试验验证。
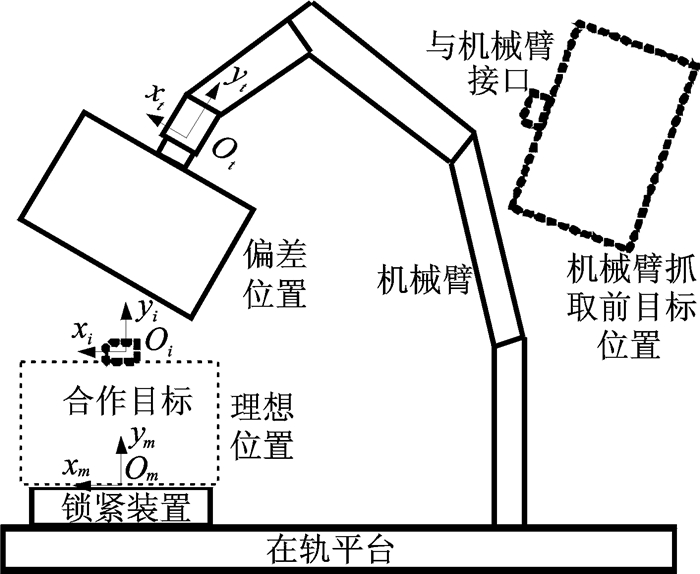
1 重复锁紧与分离装置工作流程及原理 1.1 工作流程重复锁紧与分离装置和空间机械臂位于在轨服务飞行器平台上,如图 1所示。地面发出工作指令,在轨服务飞行器平台运动到空间指定位置,然后空间机械臂末端执行器捕获轨道上待维护合作目标并将其转移到飞行器平台预设位置,随后机械臂由工作模式切换为随动模式。此时,重复锁紧与分离装置开始工作,完成对合作目标的捕获和锁紧工作,进而实现对合作目标的维护工作,分离过程为捕获和锁紧的逆过程。
|
图 1 在轨服务飞行器平台示意图 Figure 1 Schematic diagram of on-orbit service vehicle platform |
图 1中Ot-xtytzt为空间机械臂末端执行器坐标系,Oi-xiyizi为在轨服务飞行器平台预设点坐标系,Om-xmymzm为重复锁紧与分离装置坐标系。
1.2 容差性能指标空间机械臂的臂杆通常采用复合材料制造,臂杆之间的关节一般采用行星轮系或者谐波减速器传动[12],因此空间机械臂具有较大的柔性,从而导致空间机械臂末端执行器在低重力环境中的定位精度较低。在轨服务飞行器平台上机械臂的定位偏差如表 1所示,空间机械臂末端执行器Ot-xtytzt坐标原点相对平台预设点Oi-xiyizi坐标系在Oixi,Oiyi和Oizi方向的位置偏差分别为水平偏差Δx,水平偏差Δy和竖直偏差Δz;x,y和z轴转动偏差是指空间机械臂末端执行器坐标系相对在轨服务飞行器平台预设点坐标系沿Oixi,Oiyi和Oizi轴转动角度分别为
| 表 1 空间机械臂末端执行器定位偏差值 Table 1 Position and orientation error of space manipulator's end-effector |
由于空间机械臂末端执行器与合作目标之间定位精度和连接刚度较高,因此忽略它们之间的移动和转动偏差。如果空间机械臂末端执行器不存在定位偏差,那么合作目标位于图 1中合作目标理想位置,但由于机械臂末端执行器的定位偏差导致合作目标与重复锁紧与分离装置之间存在位姿偏差,则使得合作目标位于图 1中的偏差位置。因此,重复锁紧与分离装置需具有一定的容差能力才能完成对存在位姿偏差的合作目标的捕获和锁紧任务,合作目标质量和外形尺寸如表 2所示。
| 表 2 合作目标质量和外形尺寸 Table 2 Mass and shape values of the cooperative target |
综上所述,重复锁紧与分离装置的容差性能要求为水平和垂直方向位置偏差为±5 mm,绕三轴的转动偏差为±0.5°。
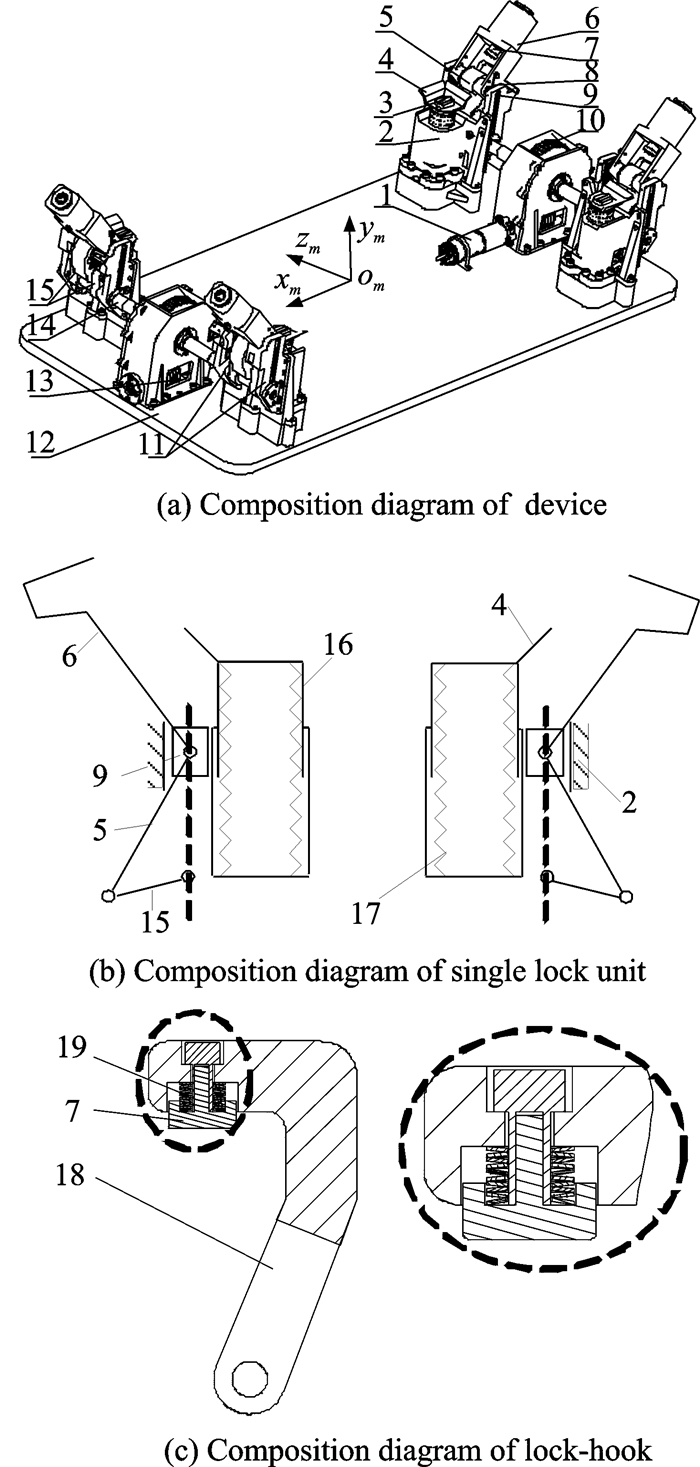
1.3 装置组成及工作原理重复锁紧与分离装置的结构组成如图 2所示。主要由4个锁紧单元、两个电机及两套传动装置组成。底座安装在固定底板的4个边角上;凹形捕获件和底座之间轴孔间隙配合,凹形捕获件上的小正方形凸台与底座的凹形槽间隙配合,在凹形捕获件和底座之间安装有圆柱弹簧,因此,凹形捕获件相对底座可以沿Omym方向运动;行程开关组件和凹形捕获件之间的安装方式与凹形捕获件和底座之间的安装方式相同;外壳通过螺钉固定在底座上;滑块组件可以沿Omym方向在外壳内滑动;锁钩组件、摇杆与滑块组件之间轴孔间隙配合;锁钩组件与滑块组件之间安装有扭簧,从而锁钩组件有向外侧偏转的趋势;球头与锁钩组件之间螺纹配合,因此可以调整球头相对锁钩组件的位置;传动轴与蜗轮、曲柄通过平键实现固连。凹形捕获件、锁钩组件和球头组成针对合作目标机械接口的捕获空间,能够弥补机械臂末端执行器的定位偏差,并且凹形捕获件形状与机械接口形状相匹配。
|
图 2 重复锁紧与分离装置组成示意图 Figure 2 Composition of reusable lock and separation device 1电机; 2底座; 3行程开关组件; 4凹形捕获件; 5摇杆; 6锁钩组件; 7球头; 8扭簧; 9滑块组件; 10蜗轮; 11外壳; 12固定底板; 13蜗杆; 14传动轴; 15曲柄; 16导向组件; 17压缩弹簧; 18锁钩; 19碟簧组件 |
收到捕获和锁紧指令后,机械臂捕获合作目标并将其移动到预设点Oi-xiyizi坐标系原点,合作目标上与重复锁紧与分离装置配合的接口进入捕获空间并触发行程开关组件中的行程开关,此时电机开始工作,从而带动传动轴运动。由于传动轴与曲柄固连,滑块组件在曲柄、摇杆以及外壳作用下沿Omym轴向下运动,而锁钩组件在滑块组件、外壳和扭簧的共同作用下逐渐摆正,并沿Omym轴向下运动。
随着锁钩组件的逐渐摆正,合作目标的机械接口在凹形捕获件和球头的共同作用下被捕获并逐渐与凹形捕获件完全配合,完成对合作目标自由度的限制和位姿的纠正。
电机继续转动,滑块组件、锁钩组件和球头沿Omym轴向下运动,合作目标的机械接口在球头作用下向下运动并压缩凹形捕获件和底座之间的圆柱弹簧,最终凹形捕获件与底座接触。至此,重复锁紧与分离装置完成对合作目标的捕获和位姿偏差的纠正,并利用曲柄滑块和蜗轮蜗杆自锁原理实现对合作目标的刚性锁紧。
收到解锁分离指令后,空间机械臂抓捕合作目标并切换为随动状态,电机反向转动完成对合作目标的解锁,同时合作目标在底座和凹形捕获件之间圆柱弹簧作用下向上运动,当锁钩组件在外壳、扭簧和滑块组件作用下向外侧偏转到初始位置时,电机停止转动,完成解锁分离工作。随后,机械臂切换为工作模式,将合作目标移动到预定轨道。
2 重复锁紧与分离装置容差性能理论分析 2.1 关键点定义和D-H矩阵凹形捕获件形状、锁钩组件尺寸、球头相对锁钩的位置、球头的运动轨迹以及机械接口外形都对重复锁紧与分离装置的容差能力有影响。
为实现合作目标的可靠捕获,需满足以下条件:(1)当机械臂把合作目标移动到预设点Oi-xiyizi坐标系原点时,机械接口与锁钩组件、球头不会发生接触碰撞且其上关键点A,B和C均应在凹形捕获件边界范围内;(2)球头关键点P和Q的运动轨迹线均应在机械接口关键点D和E点的上方。接口和球头上关键点如图 3所示。

|
图 3 机械接口和球头关键点定义 Figure 3 Key points located on mechanical interface and ball head |
机械臂末端执行器坐标相对预设点坐标变换可表示为
| $ _{\rm{I}}^{\rm{E}}\mathit{\boldsymbol{P = }}_{\rm{I}}^{\rm{E}}\mathit{\boldsymbol{T}}_{\rm{I}}^{\rm{E}}\mathit{\boldsymbol{R}} $ | (1) |
式中:IET和IER分别为空间机械臂末端执行器坐标系相对预设点坐标系的平移和转动变换矩阵。
经验证计算,当
预设点Oi-xiyizi坐标系沿Oiyi轴负方向移动h的距离后与位于固定底板中心点上的Om-xmymzm坐标系重合,假设某点在空间机械臂末端执行器坐标系下的坐标为Q1=[x1 y1 z1]T,则在Om-xmymzm坐标系下的坐标为Q=[x y z]T,它们之间的关系如式(2),IEP1表达式如式(3),IEH为预设点坐标系沿固定底板上的Om-xmymzm坐标系Omym轴移动h后的变换矩阵,即有
| $ \mathit{\boldsymbol{Q = }}_{\rm{I}}^{\rm{E}}{\mathit{\boldsymbol{P}}^1}{\mathit{\boldsymbol{Q}}^{\rm{1}}} $ | (2) |
| $ _{\rm{I}}^{\rm{E}}{\mathit{\boldsymbol{P}}^1} = _{\rm{I}}^{\rm{E}}\mathit{\boldsymbol{H}}_{\rm{I}}^{\rm{E}}\mathit{\boldsymbol{T}}_{\rm{I}}^{\rm{E}}\mathit{\boldsymbol{R}} $ | (3) |
通过式(3)可以实现合作目标以及机械接口上任意一点坐标从Ot-xtytzt坐标系到Om-xmymzm坐标系下的变换。
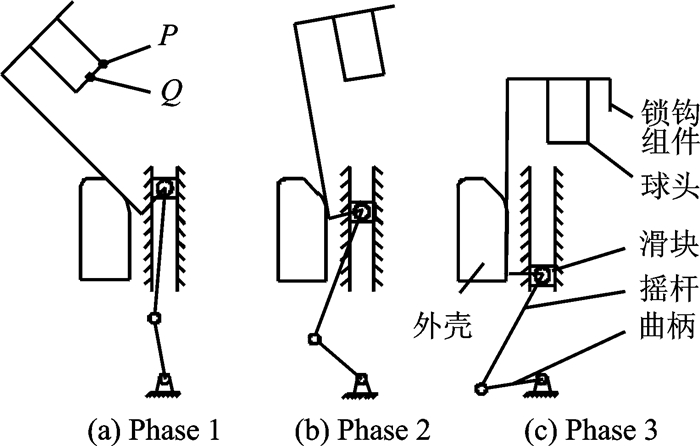
2.2 球头关键点运动轨迹数学模型锁钩组件和球头的运动过程如图 4所示。通过分析,可以将锁钩组件和球头的运动过程分解为曲线运动阶段和直线运动阶段,如图 5所示。其中O为滑块组件摆正时的转动中心,此时锁钩组件位于曲线运动阶段和直线运动阶段的过渡阶段;点O竖直向上运动Δy到达O1点,此时锁钩组件与水平方向夹角为θ,并且锁钩组件与外壳圆弧相切,切点为R;O3为外壳圆弧原点,O3点与点O在相同高度上。
|
图 4 锁钩组件和球头的运动过程示意图 Figure 4 Schematic diagram of the movement of ball head and lock-hook assembly |

|
图 5 锁钩组件和球头的运动阶段示意图 Figure 5 Schematic diagram of the movement phase of ball head and lock-hook assembly |
对各结构尺寸进行参数化定义:a为滑块组件到外壳水平距离,b为球头中点P点到锁钩组件距离,c为球头Q点到锁钩组件距离,h为球头底端到滑块组件转动中心的垂直距离,外壳圆弧半径为r,外壳圆弧角度为α。
球头关键点P和Q的运动轨迹可表示成与O1点位移Δy相关的函数,其中曲线段函数分别如式(4)和式(5)所示,直线段函数分别如式(6)和式(7)所示。
| $ \left\{ \begin{array}{l} x =-h{\rm{sin}}\theta {\rm{ + (}}\mathit{b}{\rm{-}}\mathit{a}{\rm{)cos}}\theta \\ y = \Delta y-(a - b){\rm{sin}}\theta {\rm{ + }}\mathit{h}{\rm{cos}}\theta \\ \theta = 2{\rm{arctan}}\frac{{\Delta y}}{{a{\rm{ + }}r}}\\ \;\;\;\;\;\;\;\;\;0 \le \Delta y \le (a + r){\rm{tan}}\left( {\frac{\alpha }{2}} \right) \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} x =-h{\rm{sin}}\theta + (c-a){\rm{cos}}\theta \\ y = \Delta y-(a - c){\rm{sin}}\theta {\rm{ + }}\mathit{h}{\rm{cos}}\theta \\ \theta = 2{\rm{arctan}}\frac{{\Delta y}}{{a + r}}\\ \;\;\;\;\;\;\;0 \le \Delta y \le (a + r){\rm{tan}}\left( {\frac{\alpha }{2}} \right) \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} x = b-a\\ y = h + \Delta y\;\;\;\;\;-41 \le \Delta y \le 0 \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} x = c-a\\ y = h + \Delta y\;\;\;\;-41 \le \Delta y \le 0 \end{array} \right. $ | (7) |
利用所建立的D-H矩阵,通过MATLAB编程计算得出机械接口A,B和C这3点在Om-xmymzm坐标系下的可能位置,同时在MATLAB中绘制凹形捕获件在Om-xmymzm坐标系下的外形曲线,将机械接口A,B和C这3点的可能位置与凹形捕获件外形曲线投影到xmOmzm,xmOmym和ymOmzm平面上进行比较,如图 6所示,图中的点表示A,B和C在Om-xmymzm坐标系下的可能位置,实线表示凹形捕获件的外形轮廓。

|
图 6 机械接口关键点和凹形捕获件投影位置关系 Figure 6 Projection relationship between key points of mechanical interface and concave capture part |
根据图 7的投影视图可以得出,机械接口关键点A,B和C均在凹形捕获件轮廓的捕获范围内,因此凹形捕获件可以实现对机械接口的初步捕获。

|
图 7 机械接口关键点与锁钩组件和球头投影位置关系 Figure 7 Projection relationship between key points of mechanical interface and ball head, assembly of look-hook |
将机械接口D,E,F,G,H,I,J和K这8个点在Om-xmymzm坐标系下的可能位置通过MATLAB编程计算得出,同时在MATLAB中绘制锁钩组件和球头在Om-xmymzm坐标系下的外形曲线,将机械接口8个点的可能位置与锁钩组件和球头外形曲线投影到ymOmzm和xmOmym平面上进行比较分析,如图 7所示,图中点表示D,E,F,G,H,I,J和K在Om-xmymzm坐标系下的可能位置,实线表示锁钩组件和球头的外形轮廓。
根据图 7的投影视图可以得出,当机械臂把合作目标移动到预设点Oi-xiyizi坐标系原点时,机械接口与锁钩组件和球头不会发生接触碰撞。
考虑到零部件安装尺寸的限制和球头关键点P,Q运动轨迹应在机械接口关键点D,E的上方,将球头关键点运动轨迹数学模型中的参数进行取值,得到a=20 mm,b=10 mm,c=19.5 mm,r=0.3 mm,h=43 mm和α=45°。通过MATLAB编程计算得出在捕获合作目标机械接口的过程中,球头关键点P和Q运动轨迹在xmOmym平面上投影,如图 8所示,图中点表示D和E, H和I在xmOmym平面上可能位置的投影,实线表示锁钩组件和球头的外形轮廓。

|
图 8 球头关键点运动轨迹与机械接口关键点投影关系 Figure 8 Projection relationship between key points of mechanical interface and track of key points of ball head |
根据图 8的投影视图可以得出,在捕获机械接口过程中,球头关键点P和Q的运动轨迹线均在机械接口关键点D和E的上方,因此能够完成对机械接口的最终捕获。
3 重复锁紧与分离装置容差性能仿真校验 3.1 合作目标极限位姿分析当机械臂把合作目标移动到Oi-xiyizi坐标系原点时,合作目标的位姿存在无限种情况,通过分析计算选取几种合作目标的极限位姿来完成对重复锁紧与分离装置容差能力的验证。
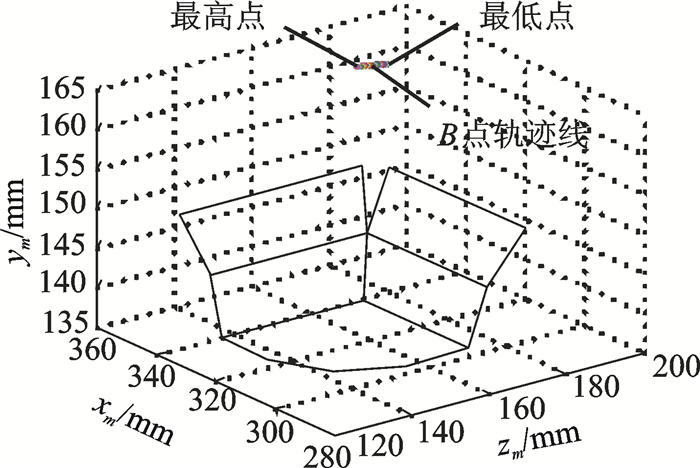
对机械接口关键点B进行分析,当机械臂末端执行器先绕Oixi轴负方向转动0.5°,再绕Ooizi轴正方向转动0.5°,此时B点相对原始位置在Oiyi方向上处于最高点,当机械臂末端执行器绕Oiyi轴正方向在-0.5°到0.5°之间转动时,B点在Oiyi方向上的高度会随着转动角度的变化而改变。通过MATLAB编程计算得出机械臂末端执行器绕Oiyi轴正方向转动时,B点位置在Om-xmymzm坐标系下的可能位置,如图 9所示。
|
图 9 B点轨迹线示意图 Figure 9 Schematic diagram of track of B point |
根据图 9可以得出,B点
轨迹最高点和最低点的差值小于0.1 mm,并且最高点和最低点分别为机械臂末端执行器绕Oiyi轴正方向转动0.5°和-0.5°,因此,机械臂末端执行器绕Oiyi轴转动对B点沿Oiyi轴方向上的位置影响很小。
综上所述,在转动偏差中,只考虑机械臂末端执行器先绕Oixi轴负方向转动0.5°,再绕Oizi轴正方向转动0.5°,最后绕Oiyi轴正方向转动0.5°或者绕Oiyi轴负方向转动0.5°的两种情况,因此合作目标极限位姿下的偏差值如表 3所示。
| 表 3 合作目标极限姿态下的位姿偏差值 Table 3 Maximum position and orientation error of cooperative target |
3.2 ADAMS模型建立及仿真
根据表 3中合作目标的位置偏差和转动偏差,建立合作目标在上述6种极限位姿下的ADAMS动力学模型,并进行仿真分析,如图 10所示。

|
图 10 重复锁紧与分离装置的容差仿真模型 Figure 10 Simulation model of reusable lock and separation device tolerance in ADAMS |
考虑到重复锁紧与分离装置的工作环境,去掉ADAMS仿真模型中的重力,以模拟太空中微重力环境。当机械臂把合作目标移动到预设点位置后,机械臂由工作模式切换为随动状态,因此在仿真过程中将重复锁紧与分离装置固定,而合作目标处于自由漂浮状态。
提取合作目标相对重复锁紧与分离装置极限位姿1,2,3,4,5和6在容差仿真过程中合作目标M点沿Omxm,Omym和Omzm轴位移随时间的变化,N点沿Omxm和Omzm轴位移随时间的变化,T点沿Omzm轴位移随时间的变化,如图 11所示。
|
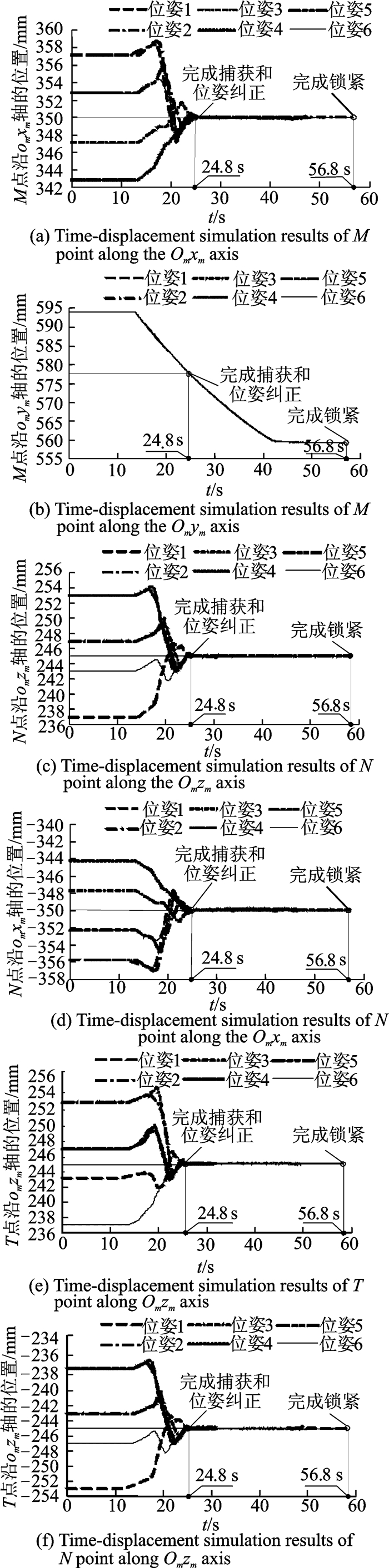
图 11 合作目标M,N和T点时间-位移仿真曲线 Figure 11 Time-displacement simulation results of the M, N and T points of the cooperative target |
图 11(c—f)分别是合作目标M,N和T点沿omzm轴位移随时间变化曲线,随着捕获过程的进行,M,N和T点在Om-xmymzm坐标系下沿Omzm轴的位置在24.8 s时分别趋向于245,245和-245 mm,并且在24.8 s和56.8 s期间,M,N和T在Omzm轴方向上的位置保持不变。因此,重复锁紧与分离装置在24.8 s时完成对合作目标绕Oixi轴和Oiyi轴转动偏差的纠正,并且完成对合作目标沿Oizi轴位置偏差的纠正。
图 11(a,d)分别是合作目标M和N点沿Omxm轴位移随时间变化曲线,随着捕获过程的进行,M和N点在Om-xmymzm坐标系下沿Omxm轴的位置在24.8 s时分别趋向于350 mm和-350 mm,并且在24.8 s和56.8 s期间,M和N点在Om xm轴方向上的位置保持不变。因此,重复锁紧与分离装置在24.8 s时完成对合作目标绕Oizi轴转动偏差的纠正,并且完成对合作目标沿Oixi轴位置偏差的纠正。
由图 11(b)的M点运动轨迹可得到,合作目标在6种极限位姿情况下均沿Omym轴平稳向下运动,直到完成锁紧。
由此可知,随着捕获过程进行,合作目标在Om-xmymzm坐标系下的位姿从捕获开始到24.8 s时间段内呈收敛趋势,并且位姿在24.8 s到完成锁紧期间保持不变。因此,重复锁紧与分离装置可以实现在合作目标的捕获和锁紧,此外验证了容差分析理论的正确性。
4 重复锁紧与分离装置容差性能试验验证 4.1 地面微重力模拟装置加工重复锁紧与分离装置样机,并设计了地面微重力模拟装置来完成对重复锁紧与分离装置容差性能的验证,如图 12所示。

|
图 12 地面微重力模拟装置 Figure 12 Micro-gravity simulation device |
地面微重力模拟装置工作原理为:采用4个配重块平衡合作目标质量,使合作目标处于自由漂浮状态,4根钢丝绳分别在两个滑轮的约束下,实现4个配重块与合作目标顶端的连接。铝型材框架2、铝型材框架3、铝型材框架4和固定架用于调整固定底板的水平度,其中铝型材框架2可以在光学平台上转动和平移,从而实现合作目标相对重复锁紧与分离装置在Ox,Oz方向的位置偏差和Oy方向的转动偏差的模拟。合作目标相对重复锁紧与分离装置在Ox,Oz方向的转动偏差可以通过调整配重块1和配重块3以及配重块2和配重块4附近合作目标的质量分布实现。
4.2 容差性能试验按表 3完成对合作目标相对重复锁紧与分离装置位姿的调整,利用地面微重力模拟装置开展对合作目标6种极限位姿下的捕获工作,如图 13所示。

|
图 13 容差性能试验 Figure 13 Misalignment tolerance experiment |
试验结果表明,重复锁紧与分离装置能够完成对合作目标6种极限位姿下的捕获和锁紧,所研制的装置容差性能满足设计指标要求。
5 结束语本文针对中国空间在轨服务任务需求,提出一种能够在机械臂协助下完成对合作目标重复锁紧与分离的方案,并对方案的容差性能进行了理论分析。此外,完成方案三维模型的建立,并在ADAMS中建立合作目标在6种极限位姿下的动力学模型,并进行容差性能仿真分析,通过仿真分析得出装置能够完成对合作目标的捕获和位姿纠正工作,验证了容差理论的正确性。加工重复锁紧与分离装置样机,并设计地面微重力装置,进行容差性能试验验证,最终确定重复重复锁紧与分离的装置容差性能满足三轴位置偏差±5 mm和三轴转动偏差±0.5°的指标。
| [1] |
李岩, 党常平.
空间在轨服务技术进展[J]. 兵工自动化, 2012, 31(5): 79–82.
LI Yan, DANG Changping. The development of orbital servicing technology in space[J]. Ordnance Industry Automation, 2012, 31(5): 79–82. |
| [2] |
丰飞. 空间大容差末端执行器及其软捕获策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 1-20.
FENG Fei. Research on space large misalignment tolerance end-effector and its soft capture strategy[D]. Harbin: Harbin Institute of Technology, 2013: 1-20. |
| [3] |
孙泽洲, 孟林智.
中国深空探测现状及持续发展趋势[J]. 南京航空航天大学学报, 2015, 47(6): 785–791.
SUN Zezhou, MENG Linzhi. Current situation and sustainable development trend of deep space exploration in China[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(6): 785–791. |
| [4] |
SULLIVAN B R. Technical and economic feasibility of telerobotic on-orbit satellite servicing[D]. Maryland, United States: University of Maryland, 2005: 1-65. |
| [5] |
陈小前, 袁建平, 姚雯, 等.
航天器在轨服务技术[M]. 北京: 中国宇航出版社, 2009: 23-104.
CHEN Xiaoqian, YUAN Jianping, YAO Wen, et al. Technologies of spacecraft on-orbit service[M]. Beijing: China Aerospace Press, 2009: 23-104. |
| [6] |
DONALD M.
On-orbit servicing of space systems[M]. Florida, United States: Krieger Publishing Company, 1993.
|
| [7] |
崔乃刚, 王平, 郭继峰, 等.
空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4): 805–811.
CUI Naigang, WANG Ping, GUO Jifeng, et al. A review of on-orbit servicing[J]. Journal of Astronautics, 2007, 28(4): 805–811. |
| [8] |
符俊. AOTV在轨维护GEO卫星的轨道控制技术研究[D]. 长沙: 国防科学技术大学, 2013: 1-22.
FU Jun. Research on orbit control technology of on-orbit maintenance to GEO satellite based on AOTV[D]. Changsha: National University of Defense Technology, 2013: 1-22. |
| [9] |
SETTELMEYER E, LEHRL E, OESTERLIN W, et al. The experimental servicing satellite-ESS[C]//International Symposium on Space Technology and Science. Omiya, Japan: [s. n. ], 1998: 617-621. |
| [10] |
KASAI T, ODA M, SUZUKI T. Results of the ETS-7 Mission-Rendezvous docking and space robotics experiments[C]//Proc Fifth International Symposium on Artificial Intelligence Robotics and Automation in Space. [S. l. ]: [s. n. ], 1999: 299. |
| [11] |
WHELAN D A, ADLER E A, WILSON S B, et al.
DARPA orbital express program:Effecting a revolution in space-based systems[J]. Small Payloads in Space, 2000, 4136: 48–56.
DOI:10.1117/12.406656
|
| [12] |
丰飞, 刘伊威, 刘宏, 等.
空间三指-三瓣式大容差末端执行器容差分析[J]. 机械设计与制造, 2014(4): 252–255.
FENG Fei, LIU Yiwei, LIU Hong, et al. Misalignment tolerance research of three fingers-three petals space end-effector with large misalignment tolerance[J]. Machinery Design & Manufacture, 2014(4): 252–255. |
 2018, Vol. 50
2018, Vol. 50


