2. 福建农林大学计算机与信息学院, 福州, 350002;
3. 东南大学移动通信国家重点实验室, 南京, 210096;
4. 台湾中华大学计算机与信息学院, 新竹, 中国
2. College of Computer and Information, Fujian Agriculture and Forestry University, Fuzhou, 350002, China;
3. National Mobile Communications Research Laboratory, Southeast University, Nanjing, 210096, China;
4. College of Computer and Information, Taiwan University of China, Hsinchu, China
近年来,到达角(Direction of arrival, DOA)估计在声纳、雷达和无线通信等领域有着重要的应用并且引起了学术界与产业界的广泛关注。同样,DOA作为方向调制(Directional modulation, DM)领域的关键技术,也显得尤为重要。估计信号一般分成两类:窄带信号和宽带信号[1]。然而传统的空间谱估计测向都是在假设所有入射信号频率相同且已知的情况下进行研究的,即入射信号为窄带信号。当入射信号为宽带信号时,与窄带信号处理不同的是,对应不同的DOA,不同的频率对应不同的信息,这就造成了DOA估计中的分集与处理增益。
宽带DOA估计的主要问题就是如何将不同频率的信息进行有效的结合以获得最准确的DOA信息。相干处理和非相干处理是宽带信号处理的两种主要类型。在非相干宽带处理中,不同频率的不同DOA将分别被独立估计,所以非相干宽带处理是窄带处理的简单扩展。它面临的主要问题是计算复杂度,因为每个频点都需要一个特征分解,且计算复杂度随着频点数量的增加而线性增加。同时由于非相干技术需要在密集网格中搜索以避免局部最小值,因此计算复杂度将提高。Yoon等提出投影子空间的正交化方法[2]本质上是一种不相干的方法,其在中等信噪比(Signal-to-noise ratio, SNR)水平下能够实现良好性能。而在相干宽带处理中,将每个频率的协方差矩阵相干的结合起来以应用于DOA估计。虽然相关宽带信号处理方法不同,但它们背后的主要原理是相同的,即使用变换矩阵将不同频率的协方差矩阵映射到中心频率的协方差矩阵,而这些不同处理方法中最主要的差异是变换矩阵的使用。文献[3~5]建立了上述宽带信号处理理论,而后又将该理论命名为相干信号子空间方法。其中变换矩阵最好为单位阵以避免焦点损失,即转换系统中的SNR损失。文献[6, 7]分别考虑了空间域中的导向协方差矩阵和重采样,进一步发展了平方变换矩阵的设计。阵列映射的另一种方法是阵列插值[8-11]。文献[12]提出信号子空间的加权平均来处理各种误差源。文献[13]中提出了贝叶斯方法用于联合估计模型阶数和DOA。最近,使用最大似然方法估计信号源和噪声功率的Wiener阵列插值技术[14-16]引起了广泛关注。它的功率估计很准确并且性能比典型的阵列插值要好,尤其在低SNR时[14]。另一个优势就是阵列插值矩阵的逆矩阵条件数提升了,并且允许在虚拟阵列比在真实阵列中有更多的传感器。当使用快速算法时,Wiener阵列插值技术效果显著。
DM作为一种安全的物理层无线传输技术,是对指定方向进行安全通信的技术。具体地说,DM是一种发射机端的技术,它能够将数字编码信号投射到预先指定的安全方向,同时扭曲该信号在其他方向的星座图。传统的DM技术主要应用于射频前端。文献[17~19]描述了依赖于近场耦合效应的DM发射机,由于所有寄生元件都是无源激励,因此又称为无源DM发射机。但是,一方面,由于被动近场衍射效应在空间方向上是复杂的,所以沿着其他未选方向的星座图以复杂且几乎不可预知的方式失真。另一方面,近场中的这种复杂的相互作用以及它们与远场的空间相关变换使得无源DM发射机的合成是一项困难且耗时的任务。Daly首先在文献[20~22]提出了简化DM合成的方法,其中DM发射机的结构由主动驱动的天线阵列组成并分别配有可重构的相移器[20-21]或辐射计[22]。基于相同的物理结构,文献[23~25]中对系统参数进行了详细研究,例如量化移相器[23]、阵元间距[24]和有源元件模式[25]。此外,增加元件间距和较高的单元辐射指向性有助于缩小安全的通信空间角度。
另一种实现DM的方式是基于基带信号的算法设计。值得注意的是,文献[26]提出了一种用矢量表示DM系统的理论,并利用该理论来实现DM的发射特性,也就是所说的正交向量法。该方法与传统的基于射频前端DM相比,利用了波束成形方案与AN,更易于在基带信号中实现,从而进一步确保在不同时隙传输不同的星座点,也更易于实现动态DM。文献[27~29]和文献[30]分别利用协作中继和最大化信泄噪比(Signal-to-leakage-noise ratio, SLNR)法来设计预编码器以实现安全通信。人工噪声(Artificial noise, AN)辅助的基于DM的随机频率分集阵列用来实现二维空间的物理层安全传输,即距离维和角度维,同时推导了遍历安全速率(Secrecy rate, SR)的下界[31]。文献[32]中提出了安全精准通信,作者将AN投影、波束成形和基于正交频分复用和DM的随机子载波选择等技术结合起来实现了有用信号的安全精准无线传输,并验证了理论分析与实际结果的一致性。
功率分配(Power allocation, PA)在DM中也极为重要。在文献[33]中,发射机同时发射有用信号和AN并且分析了不同场景下的PA问题。文献[33]推导了在存在主动窃听者且天线数为无穷多时多小区多用户超大规模多输入多输出(Multiple-input multiple-output, MIMO)系统中的渐进可实现SR,同时获得了有用信号和AN间PA的闭合表达式。另外,文献[34]考虑了非完美的信道状态信息(Channel state information, CSI)。在文献[34]中,PA策略在窃听者空间为任意分布时提出,其中PA参数可以通过在给定SR的条件下最小化安全中断概率或安全中断概率受限的情况下最大化SR得到。文献[35]分别讨论了窃听者不同谋和窃听者同谋时的PA策略。文献[36]研究了在中继干扰发射机的帮助下从控制者到激励者的安全下行传输,其中有用信号和AN间PA参数的影响通过在最小SR受限的条件下最小化安全中断概率来分析。文献[37]推导了多输入单输出单窃听、多输入单输出多窃听和多输入多输出多窃听场景中SR的下界,并且从这些下界中得到了对应的PA解决方案。文献[38]提出了更为实际MIMOME信道中AN辅助的安全传输方案,其中发射机和期望接收机的非完美CSI通过训练和模拟反馈得到,并且推导了遍历SR的闭合表达式。文中提出了一种迭代算法来优化有用信号和AN的PA同时使SR最大化,并且考虑了接收机端的CSI估计误差和发射机端的反馈误差。文献[39]研究了分布式天线系统中的安全传输问题,其中可实现遍历SR通过随机矩阵理论得到,同时作者将非凸的PA问题转化为等效的最大化最小化问题并且提出了块坐标下降法来解决该问题,从而实现安全通信。
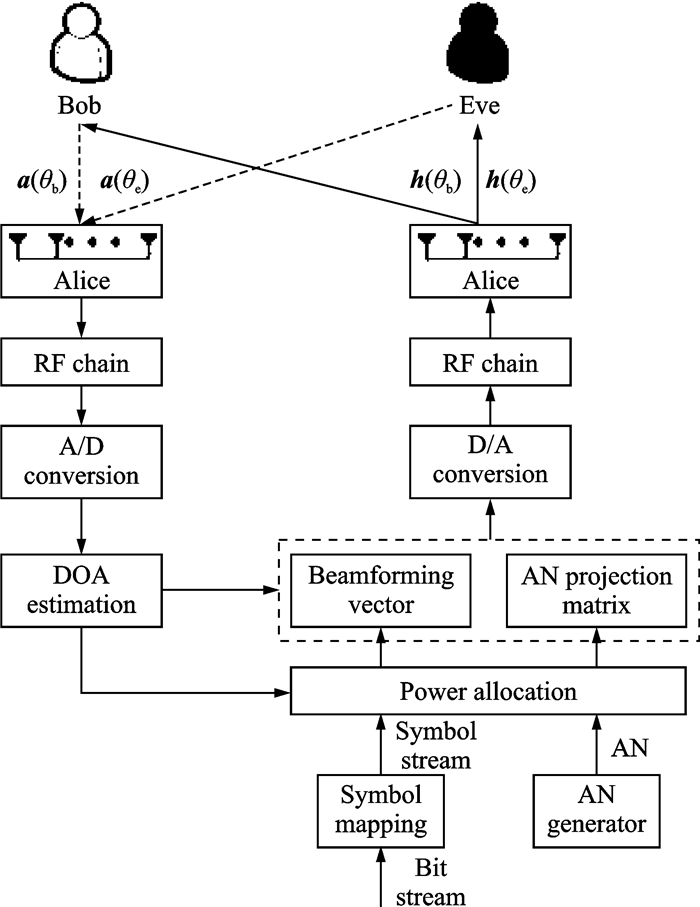
1 系统模型给定一个三节点方向调制系统模型如图 1所示,其中基站Alice采用N阵元均匀线性阵列天线,期望用户Bob和窃听用户Eve均为单天线接收机,系统工作在直达路径中。在第1时隙,基站作为接收机来估计期望方向和窃听方向的DOA;在第2时隙,Alice作为发射机,Bob和Eve作为接收机,Alice通过有用信号波束成形向量发射私密信息给Bob,同时利用AN投影矩阵阻止Eve窃听私密信息,发射机端传输的基带信号向量可表示为
| $ \mathit{\boldsymbol{s}} = \sqrt {\beta {P_{\rm{s}}}} {\mathit{\boldsymbol{v}}_{\rm{b}}}\mathit{\boldsymbol{x}} + \sqrt {\left( {1 - \beta } \right){P_{\rm{s}}}} {\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{z}} $ | (1) |
|
图 1 方向调制系统模型 Figure 1 System model of directional modulation |
式中:Ps表示总的发射功率并且是有限的;β和(1-β)分别表示私密信息和AN的功率分配因子;vb表示期望用户的归一化有用信号波束成形向量,即vbHvb=1,可将有用信号汇聚到期望方向;PAN表示归一化AN投影矩阵,即Tr[PANPANH]=1,可将发射的AN功率集中到窃听方向从而干扰非法用户的窃听;x表示有用信号并满足E{xHx}=1;z表示随机变化的AN向量且服从复高斯分布。期望接收机和窃听接收机接收的信号分别为
| $ \begin{array}{*{20}{c}} {y\left( {{\theta _{\rm{b}}}} \right) = {\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right)\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{n}}_{\rm{b}}} = }\\ {\sqrt {\beta {P_{\rm{s}}}} \mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{v}}_{\rm{b}}}\mathit{\boldsymbol{x}} + \sqrt {\left( {1 - \beta } \right){P_{\rm{s}}}} {\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{b}}}} \end{array} $ | (2) |
和
| $ \begin{array}{*{20}{c}} {y\left( {{\theta _{\rm{e}}}} \right) = {\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right)\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{n}}_{\rm{e}}} = }\\ {\sqrt {\beta {P_{\rm{s}}}} {\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{v}}_{\rm{b}}}\mathit{\boldsymbol{x}} + \sqrt {\left( {1 - \beta } \right){P_{\rm{s}}}} {\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{z}} + {\mathit{\boldsymbol{n}}_{\rm{e}}}} \end{array} $ | (3) |
式中:h(θb)和h(θe)分别为期望方向和窃听方向的导向向量,nb为期望接收机噪声,服从CN(0, σb2)分布,ne表示窃听接收机噪声,服从CN(0, σe2)分布。通常,假定σr2=σb2=σe2=σ2。根据式(2,3),可以分别获得期望方向和非期望方向的可实现速率,即
| $ R\left( {{\theta _{\rm{b}}}} \right) = {\log _2}\left( {1 + \frac{{\beta {P_{\rm{s}}}{{\left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{v}}_{\rm{b}}}} \right|}^2}}}{{\left( {1 - \beta } \right){P_{\rm{s}}}\left\| {{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right\|_2^2 + {\sigma ^2}}}} \right) $ | (4) |
和
| $ R\left( {{\theta _{\rm{e}}}} \right) = {\log _2}\left( {1 + \frac{{\beta {P_{\rm{s}}}\left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{v}}_{\rm{b}}}} \right|\left| {^2} \right.}}{{\left( {1 - \beta } \right)\left| {^2{P_{\rm{s}}}} \right.\left\| {{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right\|_2^2 + {\sigma ^2}}}} \right) $ | (5) |
根据式(4,5),可将SR定义为
| $ {R_{\rm{s}}} = {\rm{Max}}\left\{ {0,R\left( {{\theta _{\rm{b}}}} \right) - R\left( {{\theta _{\rm{e}}}} \right)} \right\} $ | (6) |
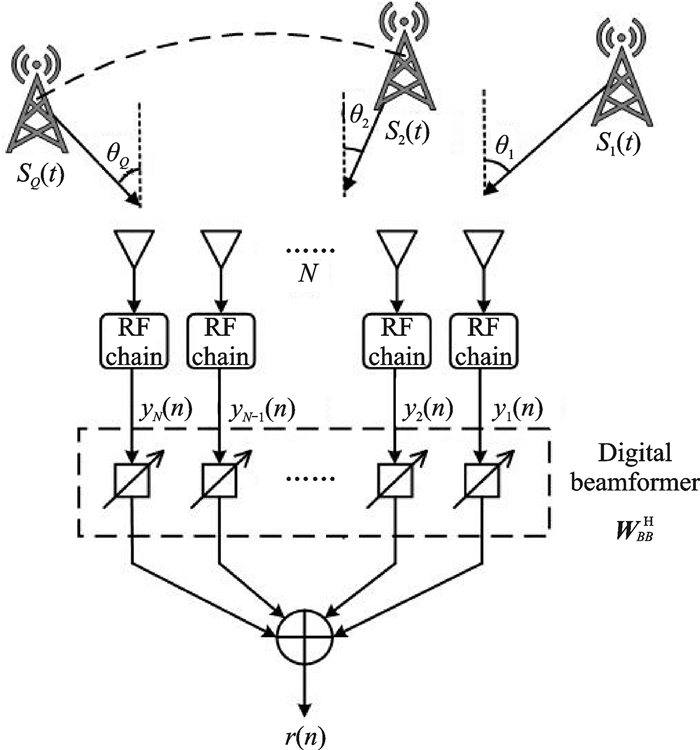
在物理层安全通信领域,DOA是非常重要的一环。精确的DOA测量能够使得期望信号准确对准期望方向,同时在窃听方向加入AN以提高安全性能。DOA估计的精确度可以通过均方误差(Mean square error, MSE)来评判,同时克拉美罗下界(Cramer-Rao bound, CRB)能够为无偏估计的精确度提供一个下界。众多学者提出并分析了许多经典的DOA估计方法。Capon DOA估计算法[40]是一种功率的最大似然估计,其目的是最大化接收信号的信干噪比(Signa-to-artificial-noise ratio, SANR)。Schmidt提出了一种广泛流传的多重信号分类(Multiple signal calssification, MUSIC)算法[41],它是一种高分辨率基于特征值的DOA估计算法。为了简化MUSIC算法因线性搜索而产生的高复杂度,根值MUSIC(Root-MUSIC)算法[42]采用寻找多项式的根的方法来估计DOA,从而大大降低了复杂度。文献[43]结合最大似然估计和MUSIC算法提出了5种方法来实现提升性能同时降低复杂度。文献[44]利用Root-MUSIC中目标函数的一阶导来估计方向角,并且性能比传统的方法更好。图 2给出了DOA估计模型。该天线阵列由N个距离为半个波长的均匀线性阵列组成,在该系统中,Q个来波信号从Q个方向到达,它们被一个有N个权值的N元天线阵列所接收。均匀线性阵列的导向向量为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}\left( {{\theta _q}} \right) = {{\left[ {1,{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }d\sin {\theta _q}}}, \cdots ,{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {N - 1} \right)d\sin {\theta _q}}}} \right]}^{\rm{T}}}}\\ {q \in \left\{ {1,2, \cdots ,Q} \right\}} \end{array} $ | (7) |
|
图 2 DOA估计模型 Figure 2 Model of DOA estimation |
通过天线阵列的每个接收信号yi(n)都含有加性零均值高斯噪声。经过射频链路中的采样,输出信号表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}\left( n \right) = \mathit{\boldsymbol{As}}\left( n \right) + \mathit{\boldsymbol{v}}\left( n \right) = }\\ {\left[ {\mathit{\boldsymbol{a}}\left( {{\theta _1}} \right),\mathit{\boldsymbol{a}}\left( {{\theta _2}} \right), \cdots ,\mathit{\boldsymbol{a}}\left( {{\theta _Q}} \right)} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}_1}\left( n \right)}\\ {{\mathit{\boldsymbol{s}}_2}\left( n \right)}\\ \mathit{\boldsymbol{M}}\\ {{\mathit{\boldsymbol{s}}_Q}\left( n \right)} \end{array}} \right] + \mathit{\boldsymbol{v}}\left( n \right)} \end{array} $ | (8) |
式中:矩阵A是由Q个导向向量a(θq)组成的N×Q的导向向量矩阵;输入信号s(n)表示时刻n入射的单一频率复信号信号组成的Q×1的向量;v(n)表示每个天线阵元的噪声向量,其均值为零,方差为σv2;y(n)是由射频链路输出组成的N×1的向量。经过数字加权后,输出信号r(n)表示为
| $ \mathit{\boldsymbol{r}}\left( n \right) = \mathit{\boldsymbol{w}}_{BB}^{\rm{H}}\mathit{\boldsymbol{y}}\left( n \right) $ | (9) |
式中wBB=[w1, w2, …, wN]T为天线的加权值。
因此,Q个信号分别以θ1, θ2, …, θQ角度到达,并被N个天线阵元所接收。为简化,将N×N的天线阵相关矩阵Ryy定义为
| $ {\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{yy}}}} = E\left[ {\mathit{\boldsymbol{y}}{\mathit{\boldsymbol{y}}^{\rm{H}}}} \right] = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{{\rm{ss}}}}{\mathit{\boldsymbol{A}}^{\rm{H}}} + {\mathit{\boldsymbol{R}}_{vv}} $ | (10) |
式中:Rss表示信源相关矩阵,Rvv=σv2I表示噪声相关矩阵,I为单位矩阵。通过求各个期望值,可以求得天线阵相关矩阵Ryy和信源相关矩阵Rss。但是,在实际情况中,噪声和来波信号的统计信息往往是未知的,于是假定该随机过程是各态历经的,用时间平均相关来近似相关,即
| $ {\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{yy}}}} = \frac{1}{L}\sum\limits_{n = 1}^L {\mathit{\boldsymbol{y}}\left( n \right){\mathit{\boldsymbol{y}}^{\rm{H}}}\left( n \right)} $ | (11) |
DOA估计技术的关键是定义一个函数,根据该函数的峰值与其对应的角度给出所估计的DOA。该函数往往被称为伪谱,伪谱定义的方法多种多样,例如,波束成形、天线相关矩阵、特征分析、线性预测、最小方差、最小范数和MUSIC等。
3 稳健波束成形设计由于无线传输的广播特性,有用信号容易被非法用户所截获,这将对无线通信网络造成严重的安全风险。因此,有用信号的传输、储存、处理和保护近些年来已成为无线通信网络中的热点研究话题[45-46]。文献[47~50]中提出用AN辅助安全传输以提高信息安全。文献[51]中提出安全DM网络的稳健合成方法以保护期望方向的安全性能,同时使非期望方向无法恢复出基带信号。此外,文中假设方向角误差为均匀分布来设计有用信号波束成形向量和AN投影矩阵。文献[52]将文献[51]的思想延伸到了广播系统中的多波DM场景,其中最大化SLNR方法用来设计有用信号波束成形向量,最大化期望方向的信号与AN之比来设计AN投影矩阵。同时,该文考虑了期望方向角完美和非完美两种情况,并假设方向角误差为截断高斯分布。在不知道方向角测量误差分布的前提下,文献[53]在多用户MIMO的场景下结合主瓣积分和泄露来设计有用信号波束成形向量和AN投影矩阵。另外,文献[54]将DM的应用扩展到多播环境中,作者提出了最大化组接收功率结合零空间投影法和基于泄露的方法来提升物理层安全和提高安全和速率。
3.1 零空间投影算法利用零空间投影算法来设计有用信号波束成形向量vb和AN投影矩阵PAN可使得AN在期望方向的影响为零,从而提升系统的安全性能。其中波束成形向量和AN投影矩阵可分别表示为
| $ {\mathit{\boldsymbol{v}}_{\rm{b}}} = \mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right) $ | (12) |
和
| $ {\mathit{\boldsymbol{P}}_{{\rm{AN}}}} = {\mathit{\boldsymbol{I}}_N} - \mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right) $ | (13) |
最大化SLNR+最大化SANR算法即在设计有用信号波束成形向量时利用最大化SLNR法,在设计AN投影矩阵时利用最大化SANR法。在期望接收机端通过最大化有用信号的SLNR来设计波束成形向量,即
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Max}}}\limits_{{\mathit{\boldsymbol{v}}_{\rm{b}}}} {\rm{SLNR}}\left( {{\mathit{\boldsymbol{v}}_{\rm{b}}}} \right)}\\ {{\rm{s}}.\;\;\;{\rm{t}}.\;\mathit{\boldsymbol{v}}_{\rm{b}}^{\rm{H}}{\mathit{\boldsymbol{v}}_{\rm{b}}} = 1} \end{array} $ | (14) |
其中
| $ {\rm{SLNR}}\left( {{\mathit{\boldsymbol{v}}_{\rm{b}}}} \right) = \frac{{\mathit{\boldsymbol{v}}_{\rm{b}}^{\rm{H}}\left[ {\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right)} \right]{\mathit{\boldsymbol{v}}_{\rm{b}}}}}{{\mathit{\boldsymbol{v}}_{\rm{b}}^{\rm{H}}\left[ {\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right) + \frac{{{\sigma ^2}}}{{\beta {P_{\rm{s}}}}}{\mathit{\boldsymbol{I}}_N}} \right]{\mathit{\boldsymbol{v}}_{\rm{b}}}}} $ | (15) |
由Rayleigh-Ritz定理可以得到最优的波束成形向量vb为下面矩阵最大特征值所对应的特征向量
| $ {\left[ {\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right) + \frac{{{\sigma ^2}}}{{\beta {P_{\rm{s}}}}}{\mathit{\boldsymbol{I}}_N}} \right]^{ - 1}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right) $ | (16) |
另外,可以通过最大化接收机端的SANR来设计AN投影矩阵,即
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{max}}}\limits_{{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} {\rm{SANR}}\left( {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;{\rm{Tr}}\left[ {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}} \right] = 1} \end{array} $ | (17) |
其中
| $ {\rm{SANR}}\left( {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right) = \frac{{\beta {P_{\rm{s}}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{v}}_{\rm{b}}}\mathit{\boldsymbol{v}}_{\rm{b}}^{\rm{H}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right)}}{{\left( {1 - \beta } \right){P_{\rm{s}}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right) + {\sigma ^2}}} $ | (18) |
优化式(17)可以等价为优化以下问题
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Min}}}\limits_{{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} {\rm{SANR}}\left( {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right) = \frac{{\left( {1 - \beta } \right){\mathit{\boldsymbol{P}}_{\rm{s}}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right)}}{{\beta {P_{\rm{s}}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{v}}_{\rm{b}}}\mathit{\boldsymbol{v}}_{\rm{b}}^{\rm{H}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right)}}}\\ {{\rm{s}}.{\rm{t}}.\;{\rm{Tr}}\left[ {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}} \right] = 1} \end{array} $ | (19) |
在vb已知的条件下,最小化式(19)可以使得目标函数的分子为零,即
| $ {\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right) = 0 $ | (20) |
因此,AN投影矩阵可以表示为
| $ {\mathit{\boldsymbol{P}}_{{\rm{AN}}}} = {\mathit{\boldsymbol{I}}_N} - \mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right) $ | (21) |
考虑方向调制中基于泄露的波束成形算法,需要利用泄露的准则来设计有用信号波束成形向量和AN投影矩阵,其中vb的设计方法与上一小节相同。同理,在非期望方向把AN看作有用信号,AN投影矩阵可以通过最大化非期望方向AN的SLNR来设计,即
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{Max}}}\limits_{{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} {\rm{SLNR}}\left( {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;{\rm{Tr}}\left[ {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}} \right] = 1} \end{array} $ | (22) |
其中
| $ \begin{array}{*{20}{c}} {{\rm{SLNR}}\left( {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right) = }\\ {\frac{{{\rm{Tr}}\left[ {\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right]}}{{{\rm{Tr}}\left\{ {\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}\left[ {\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right) + \frac{{{\sigma ^2}}}{{\left( {1 - \beta } \right){P_{\rm{s}}}}}{\mathit{\boldsymbol{I}}_N}} \right]{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}} \right\}}}} \end{array} $ | (23) |
因此,最优的AN投影矩阵由下面矩阵前N-1个最大特征值所对应的特征向量组成,则
| $ {\left[ {\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{b}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{b}}}} \right) + \frac{{{\sigma ^2}}}{{\left( {1 - \beta } \right){P_{\rm{s}}}}}{\mathit{\boldsymbol{I}}_N}} \right]^{ - 1}}\mathit{\boldsymbol{h}}\left( {{\theta _{\rm{e}}}} \right){\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {{\theta _{\rm{e}}}} \right) $ | (24) |
在研究PA问题前,先考虑基于最大化安全速率(Maximizing secrecy rate, Max-SR)的联合优化问题[55],该问题可以表示为
| $ \begin{array}{*{20}{c}} {\left( {{\rm{P1}}} \right):\mathop {{\rm{Max}}}\limits_{{\mathit{\boldsymbol{v}}_b},{\mathit{\boldsymbol{P}}_{{\rm{AN}}}},\beta } {R_{\rm{s}}}\left( \beta \right) = R\left( {{\theta _{\rm{b}}}} \right) - R\left( {{\theta _{\rm{e}}}} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;0 \le \beta \le 1}\\ {\mathit{\boldsymbol{v}}_{\rm{b}}^{\rm{H}}{\mathit{\boldsymbol{v}}_{\rm{b}}} = 1}\\ {{\rm{Tr}}\left[ {{\mathit{\boldsymbol{P}}_{{\rm{AN}}}}\mathit{\boldsymbol{P}}_{{\rm{AN}}}^{\rm{H}}} \right] = 1} \end{array} $ | (25) |
式中:Rs(β)为关于变量β的可实现SR,优化变量是PA因子β;vb为有用信号波束成形向量; PAN为AN投影矩阵。由于式(25)优化问题很难解决,接下来通过假设波束成形方法已知来解决PA问题。对任意给定的波束成形方法,很明显PA对提高SR是一种有效而重要的方法。因此,在假定vb和PAN已知的前提下,式(25)优化问题可以化简为
| $ \begin{array}{*{20}{c}} {\left( {{\rm{P2}}} \right):\mathop {{\rm{Max}}}\limits_\beta {R_{\rm{s}}}\left( \beta \right) = R\left( {{\theta _{\rm{b}}}} \right) - R\left( {{\theta _{\rm{e}}}} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;0 \le \beta \le 1} \end{array} $ | (26) |
从而可以通过拉格朗日乘子法推导出PA因子的解析式。
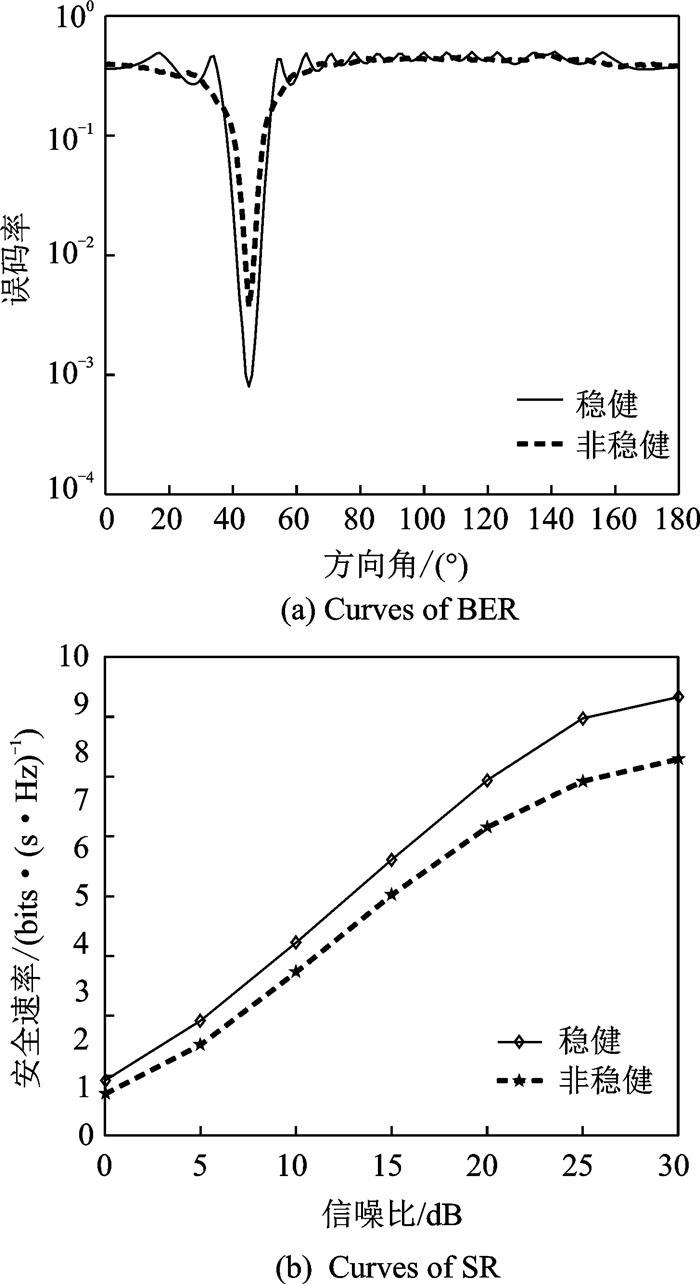
5 仿真分析在实际方向调制系统中,常常需要考虑角度误差来设计稳健的波束成形方案,为了评估零空间投影算法、最大化信泄噪比+最大化信干噪比算法、泄露算法中稳健与非稳健情况下误码率(Bit error rate, BER)和安全速率性能,选择正交相移键控(Quadrature phase shift keying, QPSK)调制方式,同时将相关参数设计如下:天线数N=16,功率分配因子β=0.9,期望方向角θb=45°,窃听方向角θe=135°,最大角度误差为Δθmax=6°且服从均匀分布。
图 3—5中分别描绘了基于零空间投影算法、最大化信泄噪比+最大化信干噪比算法和泄露算法的稳健与非稳健情况下BER和SR性能差异。从这3个图中可以发现稳健波束成形合成方法的BER和SR性能均要优于非稳健合成方法,在期望方向稳健波束成形方法的误码率更低,从而可以更好地保证信息的安全传输。另外,随着SNR的增大,两者的SR也在不断增长,但稳健波束成形方法的SR始终高于非稳健的SR,尤其在高SNR时差异更加明显,在SNR=30 dB时3种算法中稳健波束成形合成方法的性能提升分别为24.3%,29%和13.7%。

|
图 3 基于零空间投影算法的性能比较 Figure 3 Performance comparison based on null-space projection algorithm |

|
图 4 基于最大化信泄噪比+最大化信干噪比算法的性能比较 Figure 4 Performance comparison based on SLNR+SANR algorithm |
|
图 5 基于泄露算法的性能比较 Figure 5 Performance comparison based on leakage algorithm |
为了评估基于Max-SR准则的PA策略所带来的SR性能增益,将PA因子所实现的SR和一些典型的PA因子所实现的SR进行比较。图 6给出了SNR=20 dB时不同天线数情况下SR与β的关系曲线,图 7分别展示了SNR=0 dB, SNR=15 dB和SNR=30 dB时不同功率分配因子情况下SR与N的关系曲线。

|
图 6 不同天线数时SR与β的关系 Figure 6 SR versus β with different numbers of antennas |

|
图 7 不同功率分配因子时SR与N的关系 Figure 7 SR versus N with different power allocation factors |
图 6给出了天线数分别为4,16,64和256时SR与β的关系,从图 6可以发现SR是关于β的凸函数,也就是说,当β从0变化到1时存在一个独一无二的点使得SR最大。另外,通过观察可以发现,当天线数从4增加到256时,最优的β值也在增大,即当天线数增多时需要有更多的功率用来发射有用信号。
从图 7可以看出,随着天线数的增多和SNR的增大,SR在不断增长,但与典型的PA因子相比,最优PA因子β*所实现的SR始终处于最优位置。当天线数为256时,与β=0.2时的SR相比,最优PA因子β*所实现的SR增益百分比分别为118.8%,38.3%和20.9%,这些增益都是十分明显的。因而合理地分配有用信号功率和AN功率可以很好地实现SR的提升,从而保证有用信号的安全传输。
6 结论随着近5年的蓬勃发展,方向调制正在演变为无线通信与移动网络领域的热点研究领域,受到学术界与工业界的日益关注,未来具有广泛的应用场景与潜质,有望应用于飞行器组网、物联网、卫星通信、无人机网络和车联网等。经过前期的研究,本文认为以下几个方面将成为未来研究的热点:
(1) 机器学习与方向调制。在未来的研究中,可将机器学习将引入DM系统实现高性能的DOA估计。首先可以通过传统的DOA估计算法估计多次角度测量值,形成训练数据集合,然后通过参数化的机器学习例如稀疏的贝叶斯学习等方法获取方向角测量误差分布的统计参数,如均值和方差,最后预测DOA的概率密度函数,进而显著提升在中低噪比区间的DOA估计精度。
(2) 基于混合波束成形的方向调制。由于模拟波束成形结构相对简单且仅支持单流传输,而数字波束成形结构虽然支持多流传输但功耗高、成本高,所以混合波束成形结构将成为未来的研究重点[56]。混合波束成形结构不仅能够支持多流传输,而且相比数字成形结构而言具有更好的能效性。因此,在今后的研究中可以考虑将混合波束成形结构与DM相结合,从而提升系统的安全性和高效性。
(3) 多径人为噪声汇聚效应。由于大量的文献都是考虑直达路径,然而在无线通信信道中,电波传播除了直射波和地面反射波之外,在传播过程中还会有各种障碍物所引起的散射波,产生多径传播,进而导致在接收机形成人为噪声汇聚效应。此效应将极大恶化期望接收机接收性能。因此,如何更好地解决多径人为噪声汇聚效应所带来的性能恶化问题是DM网络未来面临挑战性问题,若此问题解决,未来将极大拓展其应用领域。
| [1] |
TUNCER T E, FRIEDLANDER B.
Classical and modern direction-of-arrival estimation[M]. Burlington, MA: Academic Press, 2009.
|
| [2] |
YOON Y, KAPLAN L M, MCCLELLAN J H.
New DOA estimator for wideband signals[J]. IEEE Trans Signal Process, 2006, 54(6): 1977–1989.
DOI:10.1109/TSP.2006.872581
|
| [3] |
HUNG H, KAVEH M.
Focusing matrices for coherent signal-subspace processing[J]. IEEE Trans Signal Process, 1988, 36(8): 1272–1281.
DOI:10.1109/29.1655
|
| [4] |
WANG H, KAVEH M.
Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J]. IEEE Trans Signal Process, 1985, 33(4): 823–831.
DOI:10.1109/TASSP.1985.1164667
|
| [5] |
WANG H, KAVEH M.
On the performance of signal-subspace processing-part Ⅱ:Coherent wideband systems[J]. IEEE Trans Signal Process, 1987, 35(11): 1583–1591.
DOI:10.1109/TASSP.1987.1165085
|
| [6] |
KROLIK J, SWINGLER D.
Multiple broadband source location using steered covariance matrices[J]. IEEE Trans Signal Process, 1989, 37(10): 1481–1494.
DOI:10.1109/29.35386
|
| [7] |
KROLIK J, SWINGLER D.
Focused wideband array processing by spatial resampling[J]. IEEE Trans Signal Process, 1990, 38(2): 356–360.
DOI:10.1109/29.103073
|
| [8] |
BRONEZ T P. Sector interpolation of non-uniform arrays for efficient high-resolution bearing estimation[C]//Int Conf Acoust Speech Signal Process. New York: IEEE, 1988: 2885-2888. |
| [9] |
FRIEDLANDER B.
The root-MUSIC algorithm for direction finding with interpolated arrays[J]. Signal Process, 1933, 30(1): 15–29.
|
| [10] |
FRIEDLANDER B, WEISS A J.
Direction finding using spatial smoothing with interpolated arrays[J]. IEEE Trans Aerosp Electron Syst, 1992, 28(2): 574–587.
DOI:10.1109/7.144583
|
| [11] |
HYBERG P, JANSSON M, OTTERSTEN B.
Array interpolation and DOA MSE reduction[J]. IEEE Trans Signal Process, 2015, 53(12): 4464–4471.
|
| [12] |
ELIO D, CLAUDIO D, PARISI R.
Waves:Weighted average of signal subspace for robust wideband direction finding[J]. IEEE Trans Signal Process, 2001, 49(10): 2179–2191.
DOI:10.1109/78.950774
|
| [13] |
REILLY Ng W, KIRUBARAJAN J P, LAROCQUE T J.
Wideband array signal processing using MCMC methods[J]. IEEE Trans Signal Process, 2005, 53(2): 411–426.
DOI:10.1109/TSP.2004.838934
|
| [14] |
KAYA YASAR T, TUNCER T E. Wideband DOA estimation for nonuniform linear arrays with Wiener array interpolation[C]//Fifth IEEE Sensor Array and Multichannel Signal Processing Workshop. [S. l. ]: IEEE, 2008: 207-211. |
| [15] |
TUNCER T E, KAYA YASAR T, FRIEDLANDER B.
DOA estimation for nonuniform linear arrays by using array interpolation[J]. Radio Sci, 2007, 42(4): 4002.
|
| [16] |
TUNCER T E, KAYA YASAR T, FRIEDLANDER B. Partly-filled nonuniform linear arrays for DOA estimation in multipath signals[C]//Int Conf Acoust Speech Signal Process. Hawaii: IEEE, 2007, 2: 1053-1056. |
| [17] |
BABAKHANI A, RUTLEDGE D B, HAJIMIRI A.
Transmitter architectures based on near-field direct antenna modulation[J]. IEEE Journal of Solid-State Circuits, 2008, 43(12): 2674–2692.
DOI:10.1109/JSSC.2008.2004864
|
| [18] |
ALRABADI O N, PEDERSEN G F. Directional space-time modulation: A novel approach for secured wireless communication[C]//IEEE International Conference on Communications (ICC). [S. l. ]: IEEE, 2012: 3554-3558. |
| [19] |
HONG T, SONG M Z, LIU Y.
RF directional modulation technique using a switched antenna array for physical layer secure communication applications[J]. Progress in Electromagnetics Research, 2011, 116: 363–379.
DOI:10.2528/PIER11031605
|
| [20] |
DALY M P, BERNHARD J T.
Directional modulation technique for phased arrays[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(9): 2633–2640.
DOI:10.1109/TAP.2009.2027047
|
| [21] |
DALY M P, DALY E L, BERNHARD J T.
Demonstration of directional modulation using a phased array[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(5): 1545–1550.
DOI:10.1109/TAP.2010.2044357
|
| [22] |
DALY M P, BERNHARD J T.
Beamsteering in pattern reconfigurable arrays using directional modulation[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(7): 2259–2265.
DOI:10.1109/TAP.2010.2046854
|
| [23] |
SHI H, TENNANT A. Secure physical-layer communication based on directly modulated antenna arrays[C]//Antennas and Propagation Conference (LAPC). Leicestershire: IEEE, 2012: 1-4. |
| [24] |
SHI H, TENNANT A. Tennant characteristics of a two element direction dependent antenna array[C]//Antennas and Propagation Conference (LAPC). Leicestershire: IEEE, 2011: 1-4. |
| [25] |
SHI H, TENNANT A. Secure communications based on directly modulated antenna arrays combined with multi-path[C]//Antennas and Propagation Conference (LAPC). Kunming: IEEE, 2013: 582-586. |
| [26] |
DING Y, FUSCO V F.
A vector approach for the analysis and synthesis of directional modulation transmitters[J]. IEEE Trans Antennas Propag, 2014, 62(1): 361–370.
DOI:10.1109/TAP.2013.2287001
|
| [27] |
ZOU Y, CHAMPAGNE B, ZHU W, et al.
Relay-selection improves the security-reliability trade-off in cognitive radio systems[J]. IEEE Trans Commun, 2015, 63(1): 215–228.
DOI:10.1109/TCOMM.2014.2377239
|
| [28] |
WANG H, YIN Q, XIA X.
Distributed beamforming for physical-layer security of two-way relay networks[J]. IEEE Trans Signal Process, 2012, 61(5): 3532–3545.
|
| [29] |
DONG L, HAN Z, PETROPULU A P, et al.
Improving wireless physical layer security via cooperating relays[J]. IEEE Trans Signal Process, 2010, 58(3): 1875–1888.
DOI:10.1109/TSP.2009.2038412
|
| [30] |
SADEK M, TARIGHAT A, SAYED A H.
A leakage-based precoding scheme for downlink multi-user MIMO channels[J]. IEEE Trans Wireless Commun, 2007, 6(5): 1711–1721.
DOI:10.1109/TWC.2007.360373
|
| [31] |
HU J, YAN S, SHU F, et al.
Artificial-noise aided secure transmission with directional modulation based on random frequency diverse arrays[J]. IEEE Access, 2017, 5: 1658–1667.
DOI:10.1109/ACCESS.2017.2653182
|
| [32] |
SHU F, WU X, HU J, et al.
Secure and precise wireless transmission for random-subcarrier selection-based directional modulation transmit antenna array[J]. IEEE J Sel Areas Commun, 2018, 99: 1–14.
|
| [33] |
WU Y, SCHOBER R, NG D K, et al. Secure massive MIMO transmission in the presence of an active eavesdropper[C]//IEEE ICC. [S. l. ]: IEEE, 2015: 1434-1440. |
| [34] |
ZHENG T, WANG H.
Optimal power allocation for artificial noise under imperfect CSI against spatially random eavesdroppers[J]. IEEE Trans Veh Technol, 2016, 65(19): 8812–8817.
|
| [35] |
ZHOU X, MCKAY M R.
Secure transmission with artificial noise over fading channels:Achievable rate and optimal power allocation[J]. IEEE Trans Veh Technol, 2010, 59(8): 3831–3842.
DOI:10.1109/TVT.2010.2059057
|
| [36] |
HU L, WEN H, WU B, et al.
Cooperative jamming for physical layer security enhancement in internet of things[J]. IEEE Internet Things J, 2018, 5(1): 219–228.
DOI:10.1109/JIOT.2017.2778185
|
| [37] |
TSAI S, POOR H V.
Power allocation for artificial-noise secure MIMO precoding systems[J]. IEEE Trans Signal Process, 2014, 62(13): 3479–3493.
DOI:10.1109/TSP.2014.2329273
|
| [38] |
WANG H, WANG C, WING KWAN Ng D.
Artificial noise assisted secure transmission under training and feedback[J]. IEEE Trans Signal Processing, 2015, 63(23): 6285–6298.
DOI:10.1109/TSP.2015.2465301
|
| [39] |
WANG H, WANG C, WING KWAN Ng D, et al.
Artificial noise assisted secure transmission for distributed antenna systems[J]. IEEE Trans Signal Process, 2016, 64(15): 4050–4064.
DOI:10.1109/TSP.2016.2558164
|
| [40] |
CAPON J.
High-resolution frequency-wavenumber spectrum analysis[J]. IEEE Proc, 1969, 57(8): 1408–1418.
DOI:10.1109/PROC.1969.7278
|
| [41] |
SCHMIDT R.
Multiple emitter location and signal parameter estimation[J]. IEEE Trans Antennas Propag, 1986, 34(3): 276–280.
DOI:10.1109/TAP.1986.1143830
|
| [42] |
BARABELL A. Improving the resolution performance of eigenstructurebased direction-finding algorithms[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). Boston, MA: IEEE, 1983: 336-339. |
| [43] |
WANG W, CHAI R F, GAO F. An improved Root-MUSIC algorithm and MSE analysis[C]//2016 International Conference on Computer, Information and Telecommunication Systems (CITS). Kunming: IEEE, 2016: 1-4. |
| [44] |
RAO B D, HARI K V S.
Performance analysis of Root-MUSIC[J]. IEEE Trans Acoustics Speech Signal Process, 1989, 37(12): 1939–1949.
DOI:10.1109/29.45540
|
| [45] |
SHU F, WAN S, YAN S, et al.
Secure directional modulation to enhance physical layer security in IoT networks[J]. IEEE Internet Things J, 2018(99): 1–9.
|
| [46] |
YU H, WAN S, CAI W, et al.
GPI-based secrecy rate maximization beamforming scheme for wireless transmission with AN-aided directional modulation[J]. IEEE Access, 2018, 6(1): 12044–12051.
|
| [47] |
GOEL S, NEGI R.
Guaranteeing secrecy using artificial noise[J]. IEEE Trans Wireless Commun, 2008, 7(6): 2180–2189.
DOI:10.1109/TWC.2008.060848
|
| [48] |
ZHAO N, YU F R, LI M, et al.
Physical layer security issues in interference-alignment-based wireless networks[J]. IEEE Commun Mag, 2016, 54(8): 162–168.
DOI:10.1109/MCOM.2016.7537191
|
| [49] |
YAN S, ZHOU X, YANG N, et al.
Artificial-noise-aided secure transmission in wiretap channels with transmitter-side correlation[J]. IEEE Trans Wireless Commun, 2016, 15(12): 8286–8297.
DOI:10.1109/TWC.2016.2613860
|
| [50] |
YANG N, YAN S, YUAN J, et al.
Artificial noise:Transmission optimization in multi-input single-output wiretap channels[J]. IEEE Trans Commun, 2015, 63(5): 1771–1783.
DOI:10.1109/TCOMM.2015.2419634
|
| [51] |
HU J, SHU F, LI J.
Robust synthesis method for secure directional modulation with imperfect direction angle[J]. IEEE Commun Lett, 2016, 20(6): 1084–1087.
DOI:10.1109/LCOMM.2016.2550022
|
| [52] |
SHU F, WU X, LI J, et al.
Robust synthesis scheme for secure multi-beam directional modulation in broadcasting systems[J]. IEEE Access, 2016, 4: 6614–6623.
DOI:10.1109/ACCESS.2016.2614825
|
| [53] |
SHU F, ZHU W, ZHOU X, et al.
Robust secure transmission of using main-lobe-integration based leakage beaforming in directional modulation MU-MIMO systems[J]. IEEE Syst J, 2017(99): 1–11.
|
| [54] |
SHU F, XU L, WANG J, et al.
Artificial-noise-aided secure multicast precoding for directional modulation systems[J]. IEEE Trans Veh Technol, 2018(99): 1–5.
|
| [55] |
WAN S, SHU F, LU J, et al.
Power allocation strategy of maximizing secrecy rate for secure directional modulation networks[J]. IEEE Access, 2018(99): 1–7.
|
| [56] |
SHU F, QIN Y, LIU T, et al.
Low complexity and high-resolution DOA estimation for hybrid analog and digital massive MIMO receive array[J]. IEEE Trans Commun, 2018(99): 1–14.
|
 2018, Vol. 50
2018, Vol. 50


