舰载机是航母编队主要战斗力来源,目前,排除极少数具有垂直起降功能的固定翼舰载机外,通常固定翼舰载机在航母上采用的起飞方式为:滑跃起飞和弹射起飞。相比于传统的滑跃起飞,科技含量更高、功能更强大的弹射起飞具有有效提高舰载机的起飞重量、提升舰载机的出机率等优势。因此,弹射起飞技术成为了航母战斗群攻击力的关键保证[1]。
舰载机舰上弹射起飞技术难度高,存在着影响因素多、动态响应过程复杂和物理参数变化剧烈[2]等特点。目前,国内对舰载机舰上弹射起飞已经开始展开了深入的研究,通过对弹射起飞过程建立三自由度模型或六自由度模型进行仿真分析[3, 4],研究不同弹射参数,如弹射末速度[5]、起落架突伸力[6]、载舰运动[7]、偏心偏距[8]以及大气环境[9]等因素对舰载机弹射起飞特性的影响。由于舰上弹射起飞难度大、风险高,因此为降低风险、深入了解飞机弹射特性与弹射装置特性,在开展舰上弹射起飞试验前,一般会预先开展陆上弹射起飞技术的研究,由于技术敏感度等原因,可供参考借鉴的国外研究文献较少,目前国内航空领域对舰载机舰上弹射起飞的研究较多,并针对舰上弹射起飞特点提出了适合舰载机弹射起飞的适配参数范围,其中包括飞机质量、起落架突伸力、舵偏角以及弹射装置弹射力等参数的综合适配边界[10, 11],如文献[5]提出了基于起飞质量、弹射能量和升降舵预置偏角3个参数的安全准则,文献[11]提出了电磁推力和前起落架突伸力的安全弹射起飞适应范围;但针对舰载机陆上弹射起飞的研究却鲜有涉及。本文基于弹射起飞仿真模型对某型飞机开展陆上弹射起飞过程仿真分析,获得了不同弹射参数对弹射起飞特性的影响,并针对陆上弹射起飞特点,根据舰载机舰上弹射起飞的安全准则[12]设计制定了陆上弹射起飞的基本安全准则,以此准则为基础,划分出不同弹射参数设置的弹射安全区域,首次较为系统全面地完成了对陆上弹射起飞的研究。
1 弹射起飞模型飞机陆上弹射起飞过程可以分为3个阶段:
(1) 弹射滑跑阶段
飞机在该阶段通过借助弹射装置迅速获得大速度,以保证飞机在较短时间和滑跑距离的条件下达到起飞离地速度。
(2) 自主滑跑阶段
飞机与弹射装置分离后,通过利用自身发动机推力继续加速达到抬前轮速度,满足起飞拉起条件。
(3) 起飞拉起阶段
飞机在达到抬前轮速度后,操控飞机出舵拉起离地,完成弹射起飞。
飞机弹射起飞模型必须实现以上3个阶段的模拟仿真,通过对飞机在以上3个阶段中的运动状态分析,构建气动力模型、发动机模型、起落架模型、弹射力模型、质量特性模型、起飞操纵模型、动力学与运动学方程模型和大气环境模型,共计8个模型完成对弹射起飞模型的建立。
1.1 气动力模型气动力模型主要包括以下3类:
(1) 基本气动力系数,该项与飞机的迎角α和离地高度H相关;
(2) 舵面引起的气动力系数变化,该项与飞机升降舵、方向舵及副翼偏角相关;
(3) 飞机运动状态引起的气动力系数变化,该项与飞行速度V、三轴角速度p,q,r相关。
其中各项气动力系数和气动力矩系数的计算公式分别为式(1~3)和式(4~6),其中各项参数符号说明见表 1。
| 表 1 气动力模型参数符号说明 Table 1 Parameter symbol description of aerodynamic force model |
升力系数
| $ {C_{\rm{L}}} = {C_{{\rm{L}}{\rm{.basic}}}} + {C_{{\rm{L}}{\rm{.}}{\delta _{\rm{e}}}}} \cdot {\delta _{\rm{e}}} + {C_{{\rm{L}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot {\delta _{\rm{a}}} + {C_{{\rm{L}}{\rm{.}}{\delta _{\rm{r}}}}} \cdot {\delta _{\rm{r}}} $ | (1) |
阻力系数
| $ {C_{\rm{D}}} = {C_{{\rm{D}}{\rm{.basic}}}} + {C_{{\rm{D}}{\rm{.}}{\delta _{\rm{e}}}}} \cdot {\delta _{\rm{e}}} + {C_{{\rm{D}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot {\delta _{\rm{a}}} + {C_{{\rm{D}}{\rm{.}}{\delta _{\rm{r}}}}} \cdot {\delta _{\rm{r}}} $ | (2) |
侧力系数
| $ {C_{\rm{Y}}} = {C_{{\rm{Y}}{\rm{.basic}}}} + {C_{{\rm{Y}}{\rm{.}}{\delta _{\rm{e}}}}} \cdot {\delta _{\rm{e}}} + {C_{{\rm{Y}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot {\delta _{\rm{a}}} + {C_{{\rm{Y}}{\rm{.}}{\delta _{\rm{r}}}}} \cdot {\delta _{\rm{r}}} $ | (3) |
俯仰力矩系数
| $ \begin{array}{l} {C_{\rm{m}}} = {C_{{\rm{m}}{\rm{.basic}}}} + {C_{{\rm{m}}{\rm{.q}}}} \cdot q \cdot \frac{c}{{2V}} + {C_{{\rm{m}}{\rm{.}}{\delta _{\rm{e}}}}} \cdot {\delta _{\rm{e}}} + {C_{{\rm{m}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot \\ \;\;\;\;\;\;\;{\delta _{\rm{a}}} + {C_{{\rm{m}}{\rm{.}}{\delta _{\rm{r}}}}} \cdot {\delta _{\rm{r}}} \end{array} $ | (4) |
偏航力矩系数
| $ \begin{array}{l} {C_{\rm{n}}} = {C_{{\rm{n}}{\rm{.basic}}}} + {C_{{\rm{n}}{\rm{.p}}}} \cdot p \cdot \frac{b}{{2V}} + {C_{{\rm{n}}{\rm{.r}}}} \cdot r \cdot \frac{b}{{2V}} + {C_{{\rm{n}}{\rm{.}}{\delta _{\rm{e}}}}} \cdot \\ \;\;\;\;\;\;\;{\delta _{\rm{a}}} + {C_{{\rm{m}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot {\delta _{\rm{a}}} + {C_{{\rm{m}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot {\delta _{\rm{r}}} \end{array} $ | (5) |
滚转力矩系数
| $ \begin{array}{l} {C_{\rm{l}}} = {C_{{\rm{l}}{\rm{.}}\beta }} \cdot \beta + {C_{{\rm{l}}{\rm{.p}}}} \cdot p \cdot \frac{b}{{2V}} + {C_{{\rm{l}}{\rm{.r}}}} \cdot r \cdot \frac{b}{{2V}} + {C_{{\rm{l}}{\rm{.}}{\delta _{\rm{e}}}}} \cdot \\ \;\;\;\;\;\;\;{\delta _{\rm{e}}} + {C_{{\rm{1}}{\rm{.}}{\delta _{\rm{a}}}}} \cdot {\delta _{\rm{a}}} + {C_{{\rm{1}}{\rm{.}}{\delta _{\rm{r}}}}} \cdot {\delta _{\rm{r}}} \end{array} $ | (6) |
综合以上气动力和气动力矩构建气动力模型。
1.2 发动机模型设定发动机安装轴线与飞机水平基准线平行,则发动机安装角为0。发动机不同转速对应的推力关系如图 1所示。飞机弹射起飞过程中采用的是转速100 %最大状态下的发动机推力。
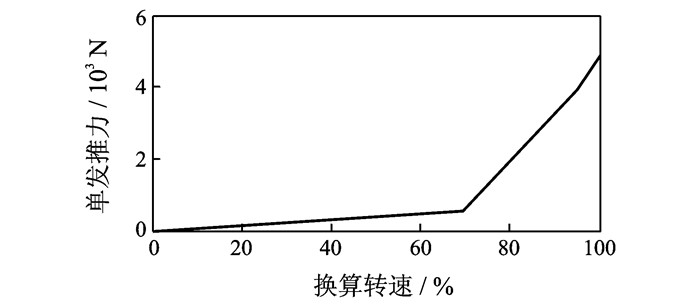
|
图 1 发动机推力随转速的变化 Figure 1 Change of engine thrust with engine′s speed |
1.3 起落架模型
典型起落架结构的支柱承受力主要包括:弹簧力和阻尼力。其中弹簧力与起落架缓冲器压缩行程sk相关,阻尼力与压缩行程变化率
| $ {F_{Nk}} = f\left( {{s_k},{{\dot s}_k}} \right) $ | (7) |
起落架支柱轴向压缩行程sk为
| $ - {s_k} = {z_{sk}} - {l_k} $ | (8) |
微分后得到起落架压缩行程变化率为
| $ - {{\dot s}_k} = {{\dot z}_{sk}} $ | (9) |
式中:lk为起落架原长;zsk为起落架与机身安装点的绝对位置,可由式(10)中飞机质心位置和飞机姿态角得到;Tgb为起落架安装点相对于质心的位置坐标;Scg2sk为通过姿态角将质心位置坐标换算为起落架安装点位置坐标的转换矩阵。
| $ \left[ {\begin{array}{*{20}{c}} {{x_{sk}}}\\ {{y_{sk}}}\\ {{z_{sk}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_{cg}}}\\ {{y_{cg}}}\\ {{z_{cg}}} \end{array}} \right] + {T_{gb}} \cdot {\mathit{\boldsymbol{s}}_{cg2sk}} $ | (10) |
起落架轴向缓冲力的反作用力即为起落架作用在机身上的作用力,因此起落架对机体的作用力和力矩为
| $ {F_{gk}} = - {F_{Nk}} $ | (11) |
| $ {M_{gk}} = {\mathit{\boldsymbol{s}}_{sk2gk}} \times \left( {\mathit{\boldsymbol{L}}_{sk.b}^{\rm{T}} \cdot {F_{gk}}} \right) $ | (12) |
式中:skg2gk为起落架与机身安装点到飞机质心的位置矢量;Lsk.bT为将起落架缓冲力转换到起落架安装点位置的转换矩阵。
1.4 弹射力模型弹射力模型的建立可以通过利用弹射速度随弹射冲程的变化,采用飞机弹射过程中的动能方程
| $ \frac{1}{2}m{v^2} = \left( {F + T - q{C_{\rm{D}}}S} \right) \cdot d $ | (13) |
式中:忽略地面摩擦力的作用,m为飞机质量,F为弹射力,T为发动机推力,q为动压,CD为阻力系数,S为机翼参考面积,d为弹射行程。
由此可以得到弹射力F与弹射行程d的变化关系。两个不同工况下(弹射末速度64 m/s,50 m/s)量纲一的弹射力与弹射行程的关系如图 2所示。
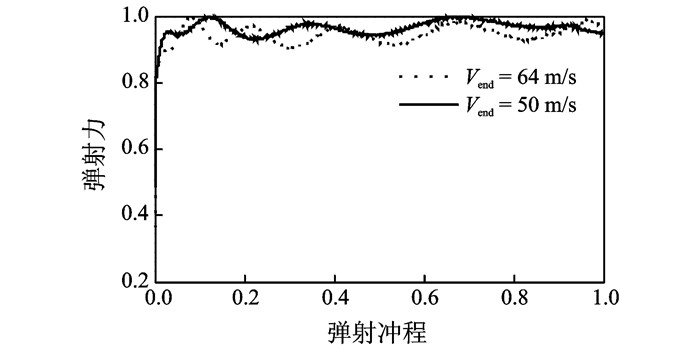
|
图 2 量纲一化弹射力随弹射行程的变化 Figure 2 Variation of dimensionless ejection force with ejection stroke |
1.5 质量特性和起飞操作模型
不同飞机的起飞质量不同,同型飞机的起飞质量因挂载、油量的不同也存在相应差异,因此通过飞机不同起飞质量对应的质心、转动惯量数据建立质量特性模型。
本文飞机弹射起飞过程中,采用的是预置舵面偏角的控制策略。通过在弹射开始前设置固定的舵面偏角提高飞机在弹射结束后的起飞拉起离地性能,而在弹射过程中不对舵面进行操控。
1.6 动力学与运动学方程模型动力学与运动学方程模型主要包括飞机六自由度动力学方程和运动学方程,由此计算得到飞机质心平动及绕质心转动的运动状态参数和相关的气动参数数据。
飞机仿真运动需基于以下基本假设前提。
(1) 飞机为刚体,建模时不考虑飞机的弹性变形;
(2) 大地平面假设,忽略地球自转,即认为地球表面为理想惯性参考系;
(3) 假设飞机质量和转动惯量在短时间尺度内不发生变化,即
(4) 机体坐标系下的XBOBZB平面为飞机质量对称平面,惯性积Ixy,Iyz均为零。
综上所述,在体轴系下建立动力学方程和运动学方程,Lgb为体轴系到地轴系的转换矩阵,其中各项参数符号说明见表 2。
| 表 2 动力学与运动学方程模型参数符号说明 Table 2 Parameter symbol description of kinetic and kinematic equation model |
动力学方程
| $ \left[ \begin{array}{l} X - mg\sin \theta \\ Y + mg\cos \theta \sin \phi \\ Z + mg\cos \theta \cos \phi \end{array} \right] = m\left[ \begin{array}{l} \dot u + qw - rv\\ \dot v + ru - pw\\ \dot w + pv - qu \end{array} \right] $ | (14) |
| $ \left[ \begin{array}{l} L\\ M\\ N \end{array} \right] = \left[ \begin{array}{l} {I_x}\dot p + \left( {{I_z} - {I_y}} \right)qr - {I_{zr}}\left( {pq + \dot r} \right)\\ {I_y}\dot q + \left( {{I_x} - {I_z}} \right)pr + {I_{zx}}\left( {{p^2} - {r^2}} \right)\\ {I_x}\dot r + \left( {{I_y} - {I_x}} \right)qr + {I_{zx}}\left( {qr - {p^2}} \right) \end{array} \right] $ | (15) |
运动学方程
| $ \left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot z} \end{array}} \right] = {\mathit{\boldsymbol{L}}_{gb}}\left[ \begin{array}{l} u\\ v\\ w \end{array} \right] $ | (16) |
| $ \left[ {\begin{array}{*{20}{c}} {\dot \phi }\\ {\dot \theta }\\ {\dot \varphi } \end{array}} \right] = \left[ \begin{array}{l} p + \tan \theta \left( {q\sin \phi + r\cos \phi } \right)\\ q\cos \phi - r\sin \phi \\ \left( {q\sin \phi + r\cos \varphi } \right)/\cos \theta \end{array} \right] $ | (17) |
飞机弹射起飞过程中,飞机动态响应过程复杂、运动状态变化剧烈以及安全影响因素多,本文选取起飞质量、弹射末速度和预置舵偏量作为影响弹射起飞特性的影响因素,以此分析不同参数设置对弹射起飞产生的有利或不利影响以及影响程度。
2.1 不同起飞质量对弹射起飞特性的影响借助弹射起飞仿真模型对某型飞机满油状态下的弹射起飞过程进行仿真计算,图中“x”表示飞机离地时刻,主要仿真工况如表 3所示,计算得到各项参数数据如图 3~5所示。
| 表 3 弹射工况 Table 3 Ejection condition |
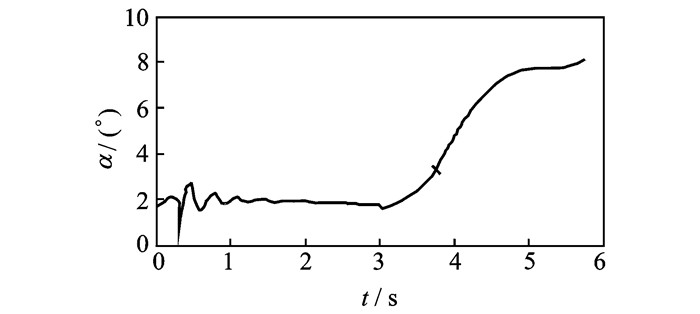
|
图 3 迎角随时间的变化 Figure 3 Changes of angle of attack with time |

|
图 4 高度随时间的变化 Figure 4 Change of height with time |
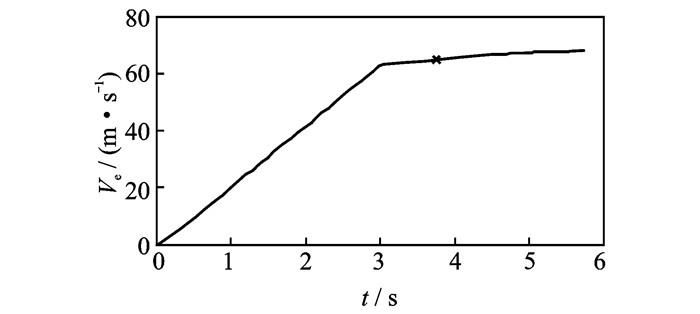
|
图 5 速度随时间的变化 Figure 5 Change of speed with time |
为对比分析不同质量对弹射起飞性能的影响,在设置相同弹射末速度和预置舵偏角的工况下本文选取了80%余油状态及半油状态进行仿真计算,得到的仿真计算结果对比如表 4所示。
| 表 4 不同质量的弹射工况 Table 4 Ejection condition of different weight |
对比分析表中数据,可以发现较小的起飞质量有利于缩短起飞滑跑距离,提高起飞性能,而对最大迎角无明显影响。
2.2 不同弹射末速度对弹射起飞特性的影响为对比分析不同弹射末速度对飞机弹射起飞特性的影响,了解飞机动态弹射过程中的运动状态变化,设置飞机在同一起飞质量和预置舵偏角的工况下,选取不同弹射末速度对飞机进行弹射起飞仿真计算,计算结果如表 5所示。
| 表 5 不同弹射末速度的弹射工况 Table 5 Ejection condition of different ejection velocity |
对比分析表中数据,可以发现设置较大的弹射末速度可以显著缩短起飞滑跑距离,但对最大迎角影响不大。
2.3 不同预置舵偏量对弹射起飞特性的影响在起飞质量和弹射末速度相同的工况下,设置不同的预置舵偏量对飞机进行弹射仿真计算,计算结果如表 6所示。
| 表 6 不同舵偏的弹射工况 Table 6 Ejection condition of different rudder deflection |
通过分析表中数据可以得到,设置不同的预置舵偏不仅影响飞机起飞滑跑距离,还对弹射起飞过程中的最大迎角存在明显影响。提高预置舵偏将缩短起飞滑跑距离,增大最大迎角。
3 陆上弹射起飞安全准则国内外还未建立起准确的陆上弹射起飞安全准则,因此本文基于Lucas提出的舰载机舰上弹射安全起飞的3条适用准则,构建陆上弹射起飞安全准则,用于指导弹射起飞参数装订,保障陆上弹射起飞安全[12]。Lucas提出的舰载机舰上弹射安全起飞的3条适用准则主要内容如下:
(1) 相对于在离舰时的质心位置,飞机的质心下沉量最大为3.048 m。
(2) 在弹射起飞离舰后,舰载机的最大迎角不能超过0.9CLmax(无动力)对应的迎角。
(3) 在舰载机离舰后出现最大下沉量后的3 s内,飞机的最大爬升率需达到3.048 m/s。如果离舰后飞机不下沉,则可以不对爬升率做限制。
上述准则中的1,3条考虑的是舰载机舰上弹射起飞离舰后,瞬间失去地效作用,升力将明显减小,据此建立了两条准则。但飞机陆上弹射起飞过程中不存在地面效应瞬间消失的现象,因此以上两条准则不适用于陆上弹射安全起飞,结合陆上弹射起飞特点,考虑到飞机在弹射分离瞬间由于前起落架突伸力的作用,可能会出现前起瞬间离地后由于速度偏小、升力不足的原因又重新触地的反复现象。这一现象有可能引发前起性能故障,进而对弹射起飞带来不可预估的风险,因此陆上弹射起飞安全准则应将上述现象列入考核指标。参考上述准则第2条,结合飞机在弹射过程中的控制策略,综合以上所述,提出了陆上弹射起飞安全准则,主要内容如下:
(1) 为了给飞机在弹射起飞后留有足够的操纵反应时间,规定飞机在离地后的2 s之内,最大迎角不得超过0.9CLmax(无动力)对应的迎角;
(2) 在弹射分离后,飞机前、主起落架依次离地,飞机不得出现起落架反复触地现象。
4 陆上弹射起飞安全区基于陆上弹射起飞安全准则,以某型飞机固定的起飞质量为标准,通过设置不同弹射末速度和预置舵偏量模拟仿真弹射起飞过程,仿真计算数据见表 7,从而最终获得该起飞质量下的陆上弹射起飞安全区。
| 表 7 弹射起飞安全边界 Table 7 Safety boundary of ejection take-off |
图 6中,Ⅰ区为满足陆上弹射起飞安全准则的最佳区域,当参数组合在Ⅰ区域内时,飞机安全起飞,前起落架不会出现反复触地现象,且迎角变化满足要求;Ⅱ区、Ⅲ区和Ⅳ区皆为不安全区域,飞机处于Ⅱ区时,在弹射分离后前起落架会反复触地;处于Ⅲ区时,若离地后2 s不进行俯仰角抑制则会出现迎角发散,给弹射起飞带来风险;Ⅳ区为危险区域,飞机既会出现前起落架反复触地现象,又会出现迎角发散现象。
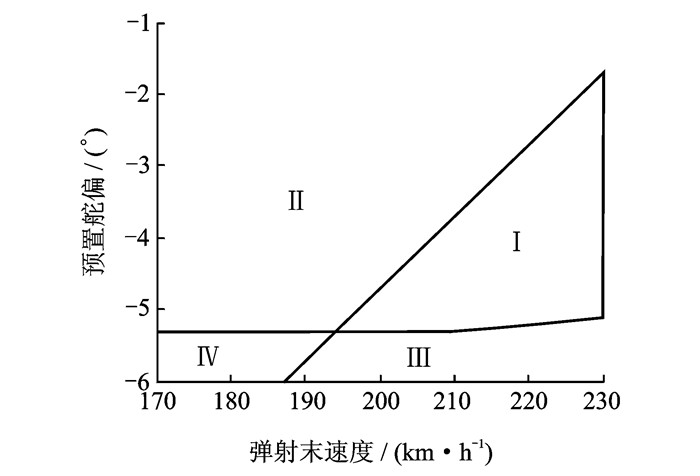
|
图 6 弹射起飞安全区 Figure 6 Safety region of ejection take-off |
5 结束语
本文利用MATLAB建模仿真技术,对飞机陆上弹射起飞过程进行模拟仿真,获得了不同起飞质量、弹射末速度和预置舵偏量对飞机弹射起飞运动过程及弹射起飞性能的影响;同时以舰载机舰上弹射起飞安全准则为依据,结合陆上弹射起飞特点,提出了陆上弹射安全准则;最后基于上述准则,借助对某型飞机陆上弹射起飞性能仿真计算,摸清了不同工况下该飞机的弹射能力,从而建立起陆上弹射起飞安全区。本文研究内容不仅为研究飞机陆上弹射起飞性能提供了一种技术手段,并且首次提出了针对陆上弹射起飞的安全准则,为分析飞机陆上弹射起飞安全性,选取合理的弹射参数提供了一种可供参考的模式。
| [1] |
陈心怡.
从瓦良格号改装看中国航母[J]. 今日科技, 2011, 10: 59–62.
DOI:10.3969/j.issn.1003-7438.2011.10.050 CHEN Xinyi. Look on Chinese aircraft carrier from refitting of varyag[J]. Today Science & Technology, 2011, 10: 59–62. DOI:10.3969/j.issn.1003-7438.2011.10.050 |
| [2] |
郭元江, 李会杰, 申功璋, 等.
复杂环境下舰载机弹射起飞环境因素建模分析[J]. 北京航空航天大学学报, 2011, 37(7): 877–881.
GUO Yuanjiang, LI Huijie, SHEN Gongzhang, et al. Modeling and analyze of the environmental factors of carrier-based aircraft catapult launch in complex environment[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(7): 877–881. |
| [3] |
王福金, 姚智慧.
舰载机的电磁弹射器研究[J]. 哈尔滨理工大学学报, 2009, 14(6): 106–110.
WANG Fujin, YAO Zhihui. Study of electronic magnetic aircraft launch system for carrier-borne aircraft[J]. Journal of Harbin University of Science and Technology, 2009, 14(6): 106–110. |
| [4] |
WANG W J, QU X J, GUO L L.
Multi-agent based hierarchy simulation models of carrier-based aircraft catapult launch[J]. Chinese Journal of Aeronautics, 2008, 21(3): 223–231.
DOI:10.1016/S1000-9361(08)60029-1
|
| [5] |
蔡丽青. 舰载机弹射起飞安全因素分析及安全准则设计[D]. 南京: 南京航空航天大学, 2014.
CAI Liqing. Safety factor analysis and safety criterion design of launching and taking off carrier based aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D672562 |
| [6] |
沈强, 黄再兴.
舰载机起落架突伸性能参数敏感性分析[J]. 航空学报, 2010, 31(3): 532–537.
SHEN Qiang, HUANG Zaixing. Sensitivity analysis of fast-extension performance of carrier based aircraft landing gear to varying parameters[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 532–537. |
| [7] |
贾忠湖, 高永, 韩维.
航母纵摇对舰载机弹射起飞的限制研究[J]. 飞行力学, 2002, 20(2): 19–21.
JIA Zhonghu, GAO Yong, HAN Wei. Research on the limitation of vertical toss to the warship-based aircraft's catapult-assisted take-off[J]. Flight Dynamics, 2002, 20(2): 19–21. |
| [8] |
于浩, 聂宏.
舰载机偏中心定位弹射起飞动力学分析[J]. 南京航空航天大学学报, 2010, 42(5): 537–542.
YU Hao, NIE Hong. Dynamics analysis of carrier-based aircraft with off-center catapult launch[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2010, 42(5): 537–542. |
| [9] |
MASLOV L A. The experience of aerodynamic disturbances research behind an aircraft-carrier ship with elements for safe operation of ship-based aircraft[C]//NATO RTO Applied Vehicle Technology Panel Symposium on Fluid Dynamics Problems of Vehicles Operating Near or in the Air-Sea Interface. Amsterdam: [s.n.], 1998. |
| [10] |
吴昊. 舰载机弹射起飞仿真及安全指标分析[D]. 哈尔滨: 哈尔滨工程大学, 2015.
WU Hao. The simulation and safety indicators analysis of aircraft catapult[D]. Harbin: Harbin Engineering University, 2015.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01105600 |
| [11] |
李静, 左斌, 路翠华.
应用电磁弹射器的舰载机起飞性能分析[J]. 海军航空工程学院学报, 2012, 27(2): 121–126.
LI Jing, ZUO Bin, LU Cuihua. Performance analysis of catapult take-off process of carrier-based aircraft using electromagnetic aircraft launch system[J]. Journal of Naval Aeronautical and Astronautical University, 2012, 27(2): 121–126. |
| [12] |
LUCAS C B. Catapult criteria for a carrier-based airplane[R]. AD702814, 1968. |
 2018, Vol. 50
2018, Vol. 50


