2. 南京航空航天大学机械结构力学及控制国家重点实验室, 南京, 210016
2. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronatics & Astronatics, Nanjing, 210016, China
常规的风洞测力试验中,风洞试验模型及其支撑装置构成了一个悬臂梁系统,主要包括试验模型、天平、尾支杆及支撑等零部件,其中试验模型悬挂于最前端,尾支杆固定在试验段中后部。风洞试验时,模型受到非定常气动力的作用,会发生与天平、支杆和支架一起振动的情况,这将对试验数据的准确带来不良影响,如果振动时间过长、幅度过大或者频率过高,甚至会损坏模型,给风洞试验的顺利完成带来一定困难,影响跨声速与超声速飞行器研究发展。分析风洞模型的动力学特性,降低模型振动,已成为必须解决的关键课题。
欧美国家率先对压电材料在风洞减振系统中的工程应用展开研究,文献[1]使用压电陶瓷作动器、采用单输入单输出纯比例的控制方法抑制1/6缩比F-18模型的垂直尾翼的局部振动;Balakrishna等[2-4]研究中心为跨声速风洞设计了主动减振系统,他们在模型与支杆的连接处采用环布式结构安装压电驱动器,可同时实现俯仰和偏航两个方向的一阶模态振动控制。除了国家跨声速设备(National transonic facility, NTF)和欧洲跨声速风洞(European transonic windtunnel, ETW)之外,其他机构也开始关注风洞支杆的减振问题,陈卫东等人[5]将压电驱动器直接装载于模型结构内,设计了一套计算机实时主动减振系统。国内关于风洞支杆振动主动控制的研究相对较少,尚未成风。
早期的风洞振动控制研究主要采用被动式控制方法,在结构上附加隔振装置来调节阻尼,但是这种方法灵活性较差,减振效果也不明显[6]。压电材料由于其响应速度快、频率范围宽、驱动能力大等诸多优点,使得在近年来基于压电智能结构的主动式振动控制方法得到了越来越广泛的应用,振动主动控制的研究热点主要集中于结构的动力学建模[7-9]和控制算法[10-16]的研究。常见的算法有最优控制[10]、自适应控制[11]、鲁棒控制[12-14]、正位置反馈(PPF)控制[15]和滑模控制[16]等,这些基于模态空间的控制算法要求建立精确被控对象的结构动力学模型,而实际工程中使用的高阶非线性强耦合系统模型都十分复杂,实现精确建模绝非易事, 且信号在传输过程中又会受到噪声的干扰,都导致了这些算法在工程应用中的开展举步维艰。
本文以风洞用悬臂式尾支杆俯仰方向一阶模态振动幅度为控制目标,设计一套以压电陶瓷叠堆作为驱动器的减振系统。控制器采用神经网络PID智能控制算法,通过地面试验研究控制参数在神经网络中的自适应性能,对比神经网络PID与经典PID的减振效果。
1 神经网络PID原理人工神经网络是对生物神经网络的理想化,由一个个人工神经元组成。人工神经元将收集的信号加权、求和(∑)、激发[f(·)]产生一个输出;其中权值影响最大,必须经历适应性训练得到。一个线性神经元按如下方法处理数据:对于给定的输入模式x1, w2, …, xn、相关的权值w1, w2, …, wn和一个带有相关权值w0的偏差输入, 首先计算出网络输入
人工神经网络中权值的影响最大,必须经历适应性训练,即设置一定的学习规则来进行连接权值的修正。本文选用最广泛的误差传播式学习规则(Delta规则),该规则提出最优权值可以在训练过程中从初始权值沿与梯度相反的方向下降得到。以一个线性神经元输入模式来描述:具有一个输入x,没有偏差输入,目标输出为r,输出为y;计算网络输入u和输出y为
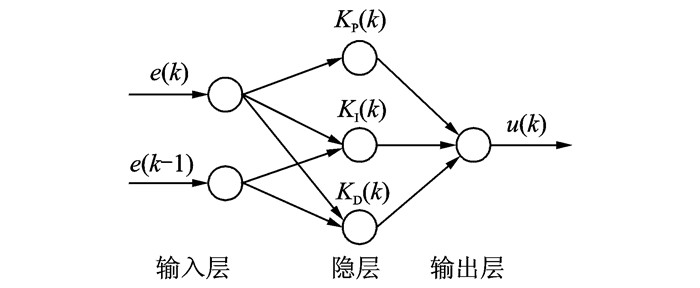
前向网络是目前研究最多的神经网络形式之一,包含输入层、隐层及输出层。实际输出的计算是按前向传播的方向来进行的,而修改权值wi则是按反方向进行的,因此称为反向传播网络(Back-propagated network, BP)。BP神经网络具有逼近任意非线性函数的能力,而且结构明确、学习方法简单。因此本文采用基于BP神经网络的参数自学习PID控制算法,其结构如图 1所示。基于BP神经网络的PID控制器由两个部分组成:(1)经典的PID控制器。直接对被控对象进行比例-积分-微分控制,3个参数可在线整定;(2)神经网络整定。根据系统的运行状态,通过神经网络的自学习、调整权系数,调节PID控制器的参数,以达到性能指标的最优。
|
图 1 神经网络PID原理图 Figure 1 Schematic of neural network PID |
2 系统设计 2.1 减振系统构成
进行吹风试验时,悬臂式尾支杆与测试模型构成的系统受到宽频带气动载荷(包括静态载荷和动态载荷)的作用,载荷沿着尾支杆的任意截面处产生动态弯矩。该系统可以被看成一个多自由度低阻尼的质量弹簧系统。在气动载荷作用下,系统的振动微分方程可表示为
| $ \mathit{\boldsymbol{M\ddot x}} + \mathit{\boldsymbol{C\dot x}} + \mathit{\boldsymbol{Kx}} = \mathit{\boldsymbol{F}} $ | (1) |
式中:M为系统的质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为系统受到气动载荷的作用力向量;x表示振动的位移向量。
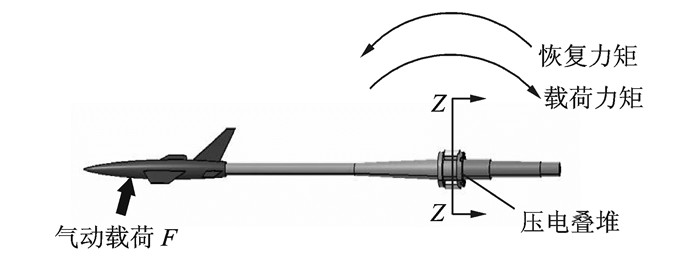
采用压电驱动器实现减振的原理如图 2所示。
|
图 2 压电驱动器减振原理 Figure 2 Principle of piezoelectric damper |
将压电驱动器安装在尾支杆的根部,通过外部施加变化的电压使驱动器产生反力矩,抵消气动载荷作用于该处产生的力矩,从而实现悬臂式尾支杆系统俯仰方向的振动抑制。
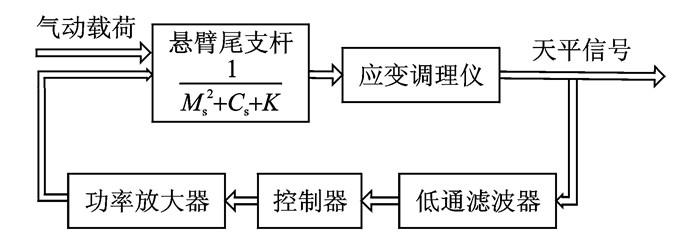
减振系统流程框图如图 3所示。吹风时,尾支杆受到气动载荷的持续激励产生振动,安装于支杆端部的测试天平配合应变调理仪,将反映支杆振动水平的机械信号转化为天平电压信号,经低通滤波器调理平滑后,进入控制器中根据控制算法计算控制信号,再由压电功率放大器将控制信号放大,生成压电驱动器所需的驱动电压。驱动器受到驱动电压产生作用力,抑制支杆的振动。由此构成一个单闭环负反馈控制系统。
|
图 3 减振系统流程框图 Figure 3 Diagram of vibration damping system |
2.2 控制器设计
本文的算例中采用自适应的线性神经元模型,采用梯度下降法(Delta规则)实现有监督的误差修正学习。经典PID的公式为
| $ u\left( k \right) = {K_{\rm{P}}}\left( k \right){e_{\rm{P}}}\left( k \right) + {K_{\rm{I}}}\left( k \right){e_{\rm{I}}}\left( k \right) + {K_{\rm{D}}}\left( k \right){e_{\rm{D}}}\left( k \right) $ | (2) |
由于r(k)=0,则
| $ \left\{ \begin{array}{l} {e_{\rm{P}}}\left( k \right) = r\left( k \right)- y\left( k \right) =- y\left( k \right)\\ {e_{\rm{I}}}\left( k \right) = \sum\limits_{j = 1}^k {{e_{\rm{P}}}\left( j \right)} =- \sum\limits_{j = 1}^k {y\left( j \right)} \\ {e_{\rm{D}}}\left( k \right) = {e_{\rm{P}}}\left( k \right) - {e_{\rm{P}}}\left( {k - 1} \right) = - [y\left( k \right)-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;y\left( {k-1} \right)] \end{array} \right. $ | (3) |
神经网络PID将3个控制参数作为BP神经网络中的权值联结点,根据Delta学习规则进行自整定。则权值的递推公式为
| $ \left\{ \begin{array}{l} {K_{\rm{P}}}\left( {k + 1} \right) = {K_{\rm{P}}}\left( k \right) + \beta \frac{{\partial \varepsilon }}{{\partial {K_{\rm{P}}}}}\\ {K_{\rm{I}}}\left( {k + 1} \right) = {K_{\rm{I}}}\left( k \right) + \beta \frac{{\partial \varepsilon }}{{\partial {K_{\rm{I}}}}}\\ {K_{\rm{D}}}\left( {k + 1} \right) = {K_{\rm{D}}}\left( k \right) + \beta \frac{{\partial \varepsilon }}{{\partial {K_{\rm{D}}}}} \end{array} \right. $ | (4) |
3个权值都采用相同的学习速率。根据链式求导法则,有
| $ \left\{ \begin{array}{l} \frac{{\partial \varepsilon }}{{\partial {K_{\rm{P}}}}} = \frac{{\partial \varepsilon }}{{\partial y\left( {k + 1} \right)}}\cdot\frac{{\partial y\left( {k + 1} \right)}}{{\partial u\left( k \right)}}\cdot\frac{{\partial u\left( k \right)}}{{\partial {K_{\rm{P}}}}}\\ \frac{{\partial \varepsilon }}{{\partial {K_{\rm{I}}}}} = \frac{{\partial \varepsilon }}{{\partial y\left( {k + 1} \right)}}\cdot\frac{{\partial y\left( {k + 1} \right)}}{{\partial u\left( k \right)}}\cdot\frac{{\partial u\left( k \right)}}{{\partial {K_{\rm{I}}}}}\\ \frac{{\partial \varepsilon }}{{\partial {K_{\rm{D}}}}} = \frac{{\partial \varepsilon }}{{\partial y\left( {k + 1} \right)}}\cdot\frac{{\partial y\left( {k + 1} \right)}}{{\partial u\left( k \right)}}\cdot\frac{{\partial u\left( k \right)}}{{\partial {K_{\rm{D}}}}} \end{array} \right. $ | (5) |
式中
| $ \left\{ \begin{array}{l} \frac{{\partial \varepsilon }}{{\partial y\left( {k + 1} \right)}} = \frac{{\partial \left[{-y\left( {k + 1} \right)} \right]}}{{\partial y\left( {k + 1} \right)}} = -1\\ \frac{{\partial y\left( {k + 1} \right)}}{{\partial u\left( k \right)}} = \frac{{y\left( {k + 1} \right) -y\left( k \right)}}{{u\left( k \right) -u\left( {k - 1} \right)}} \end{array} \right. $ | (6) |
由于[u(k)-u(k-1)]变化量较小,则取
| $ \frac{{\partial y\left( {k + 1} \right)}}{{\partial u\left( k \right)}} = {\rm{sgn}}\left[{\frac{{y\left( {k + 1} \right)-y\left( k \right)}}{{u\left( k \right)-u\left( {k-1} \right)}}} \right] $ |
最终推得神经网络PID的自学习公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{P}}}\left( {k + 1} \right) = {K_{\rm{P}}}\left( k \right) - \beta {\rm{sgn}}\left[ {\frac{{y\left( {k + 1} \right) - y\left( k \right)}}{{u\left( k \right) - u\left( {k - 1} \right)}}} \right]}\\ {{K_{\rm{I}}}\left( {k + 1} \right) = {K_{\rm{I}}}\left( k \right) - \beta {\rm{sgn}}\left[ {\frac{{y\left( {k + 1} \right) - y\left( k \right)}}{{u\left( k \right) - u\left( {k - 1} \right)}}} \right]}\\ {{K_{\rm{D}}}\left( {k + 1} \right) = {K_{\rm{D}}}\left( k \right) - \beta {\rm{sgn}}\left[ {\frac{{y\left( {k + 1} \right) - y\left( k \right)}}{{u\left( k \right) - u\left( {k - 1} \right)}}} \right]} \end{array}} \right. $ | (7) |
式中β为学习速率。β越大参数自学习越快,但过快容易陷入局部饱和;β越小参数自整定越精确,控制效果越好,但整定速度变慢,控制的动态性能会变差。
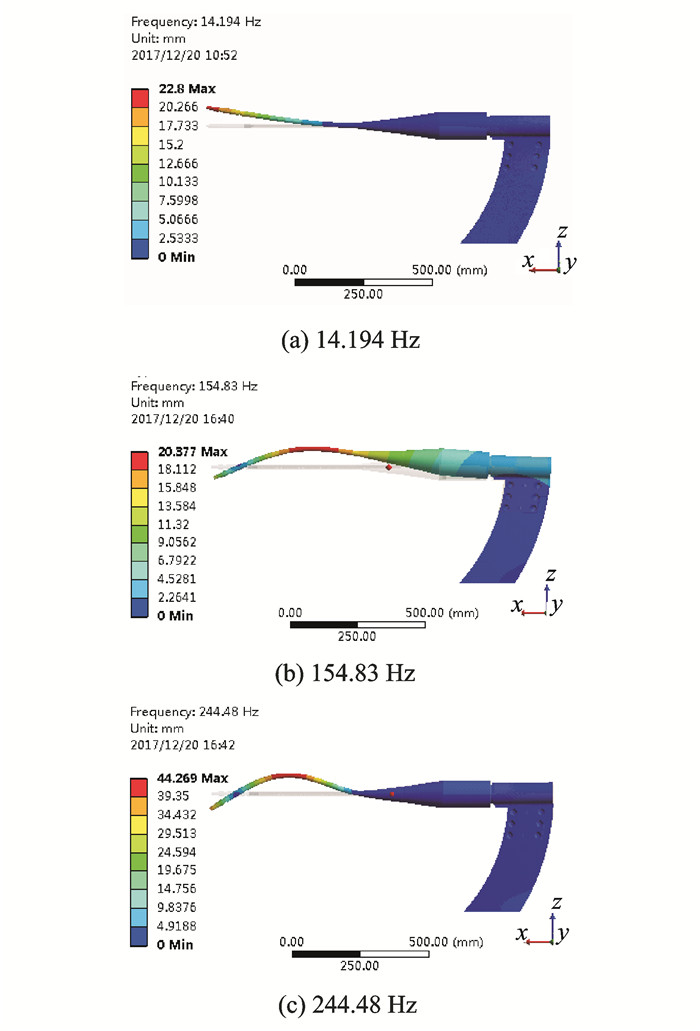
2.3 模态分析结构的固有频率与对应的模态结构形状是设计承受变化载荷条件下结构的重要参数,而模态分析的目的在于确定结构的固有频率与相应的振型。结构中压电叠堆作为驱动器件,并且主要作为动态输出使用。为了在静力学分析中压电叠堆驱动器驱动支杆结构产生的端部位移变化量很小,需要利用模态分析方法确定减振支杆结构固有频率,对压电叠堆输出接近固有频率的交变电压,达到大幅放大压电叠堆驱动支杆结构的效果。此处模态分析以静力学分析为基础,存在拉紧螺栓预紧力等预应力,预应力的存在会对其固有频率有影响。偏航与滚转方向,由于与俯仰方向的振动抑制不相关,不在控制器设计的考虑范围内,因此只考虑俯仰方向的模态。减振支杆结构俯仰方向前三阶模态振型如图 4所示。
|
图 4 尾支杆模态振型图 Figure 4 Modal shape of the sting |
由图 4可以看出俯仰方向的前三界模态频率分别为14.194,154.83和244.48 Hz。模态分析表明了尾支杆俯仰方向的主导模态是其一阶模态,由于风洞试验中动载频率多为50 Hz以下的低频段,因此一阶模态是减振的主要关注点。
3 试验及讨论为了确保控制系统的实时性与高效性,本文采用虚拟仪器技术,搭建主动控制系统试验平台,验证设计的控制算法对减振系统的有效性与稳定性。整个控制系统连接线路主要可分为采集通道和输出通道两组。采集通道由应变调理仪(ADAM 3016)、抗混叠滤波器(CM3508B)以及数采卡(NI PXI-7841R)构成,从尾支杆端部的天平获得振动信号,经应变调理仪调理放大、抗混叠滤波器滤波平滑后,得到高信噪比、幅值与数采卡输入电压允许范围相适应的信号,再输入给控制机箱;输出通道由数采卡、抗混叠滤波器、压电功率放大器组成,控制机箱从数采卡输出控制信号,经抗混叠滤波器平滑信号后,由压电功率放大器释放出高电压,最后驱动支杆上装配的封装压电陶瓷作动,达到减振的目的。其控制系统的组成如图 5所示。

|
图 5 实验系统实物图 Figure 5 Photograph of experimental setup |
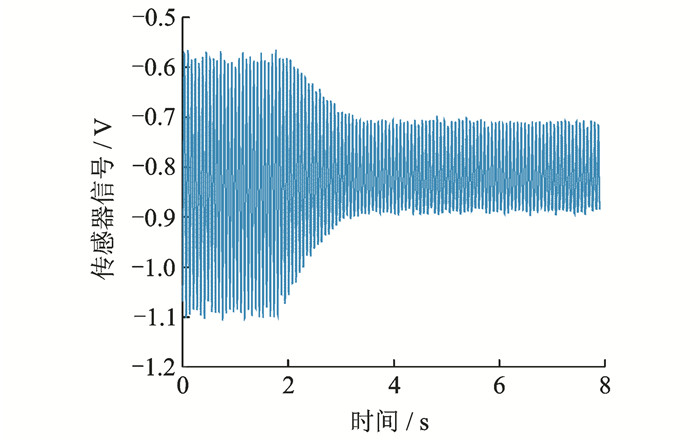
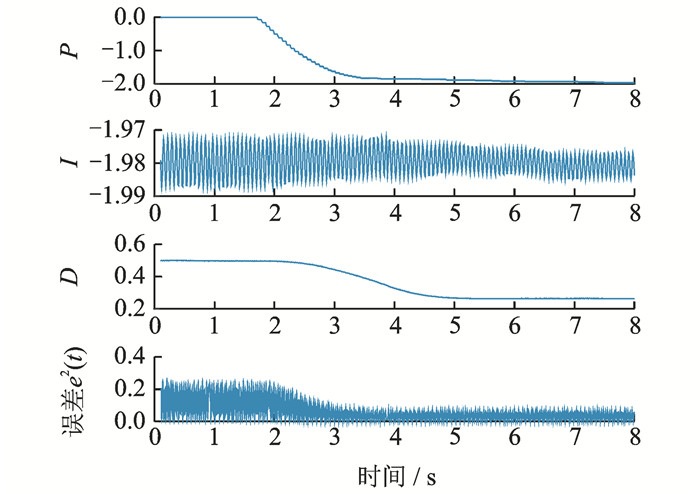
采用神经网络PID算法在线自动调整控制参数,对尾支杆进行单频率激振控制试验验证。设置学习速率β=0.016,以一阶模态频率激振的控制效果与参数整定过程如图 6~8所示。
|
图 6 神经网络PID的控制效果 Figure 6 Performance of neural network PID |
|
图 7 PID参数整定过程 Figure 7 Adjusting procedure for PID parameters |
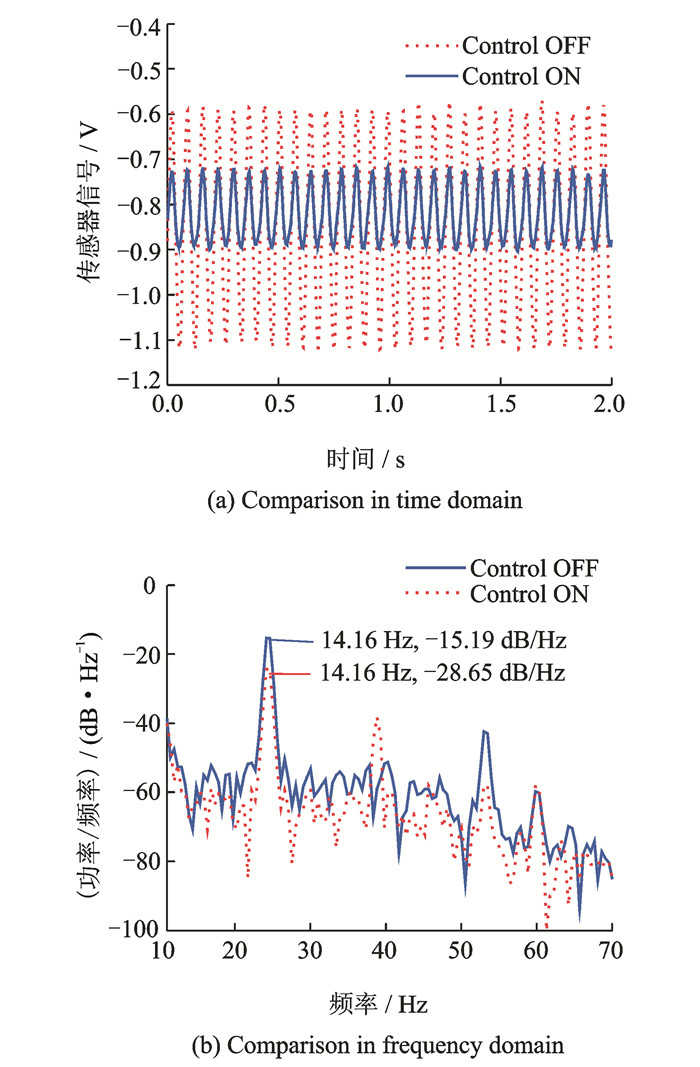
|
图 8 神经网络PID控制对比图 Figure 8 Comparison of performance between NNPID controlled and uncontrolled |
由图 6~8可以看出,振动信号的标准差由不控制时的184.0 mV降低到主动控制时的55.2 mV,振动信号的功率谱由不控制时的-15.19 dB/ Hz降低到主动控制时的-28.65 dB/Hz,功率谱下降了9.85 dB/Hz,结果表明模型支杆在连续载荷的作用下得到了有效控制。
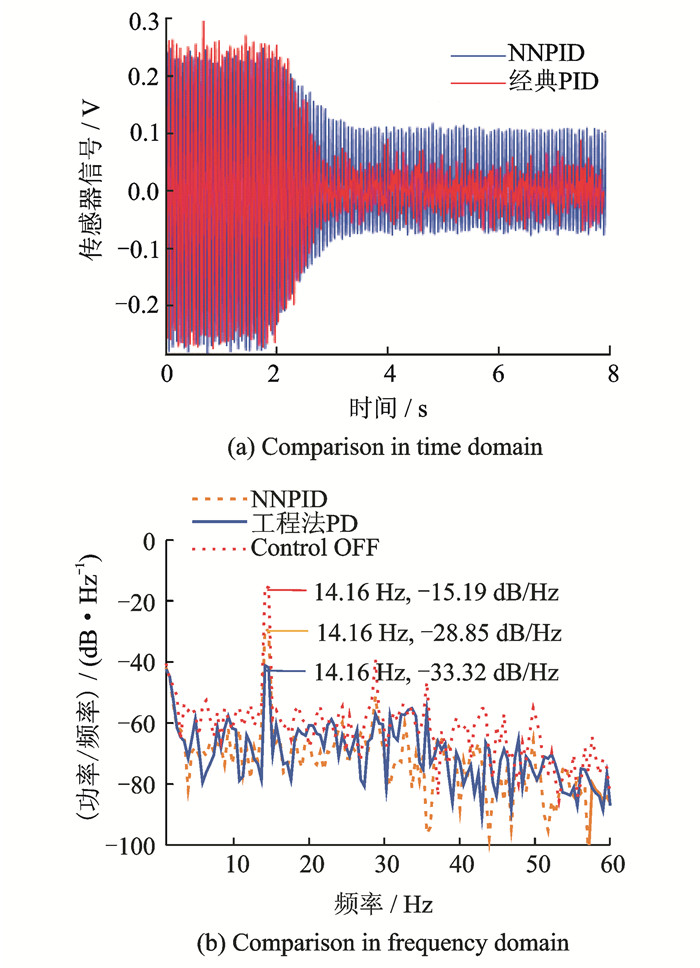
将经典PID算法结果与神经网络PID算法结果对比,其时域信号图与功率谱图如图 9所示。
|
图 9 神经网络PID与传统PID控制效果比较 Figure 9 Comparison of performance between conventional PID and neural network PID |
由图 9可以看出,采用经典PID控制算法时,振动信号的标准差由不控制时的184.0 mV降低到控制时的38.0 mV,振动信号的功率谱由不控制时的-14.91 dB/Hz降低到控制时的-33.32 dB/Hz,功率谱下降了13.02 dB/Hz;采用神经网络PID自适应控制时,振动信号的标准差下降到了55.2 mV,振动信号的功率谱降低到-28.85 dB/Hz,功率谱下降了13.66 dB/Hz。结果表明模型支杆在连续载荷的作用下,采用经典PID控制算法与神经网络PID均可达到有效控制,且神经网络PID在保证减振效果的情况下实现控制参数自整定。
值得注意的是,神经网络P ID自适应算法在应用时需要选取合适的学习速率β,学习速率过高,会使参数在自适应过程中陷入局部最优而无法达到性能指标设置的范围,此时控制参数一直会处于变化状态难以趋于稳定,控制信号不稳定同时也会导致被控支杆模型的稳定性下降,甚至引起发散使得控制失败;而学习速率过低,则会延长模型支杆被控制的过度过程,振动控制的动态性能下降,对于振动控制过度时间要求短的情况则会失去控制意义。
4 结束语本文采用人工神经网络智能控制算法对风洞用悬臂式尾支杆的减振问题进行研究,将神经网络PID与经典PID控制算法进行了试验研究与对比分析。结果显示,神经网络PID算法与经典PID控制算法均具有明显的抑振作用,降低振动幅度可达70%以上,且神经网络PID在保证控制效果的情况下可实现控制参数自适应。本研究为减振系统后续进行风洞试验验证奠定了基础。
| [1] |
WIMMEL R. Active electronic equipment DOF suspension for high loads as vibration, shock and quasi static forces[C]//Spacecraft Structures, Materials and Mechanical Testing 2005. Noordwijk, the Netherlands: Karen Fletcher, 2005, 581: 32. |
| [2] |
BALAKRISHNA S, HOULDEN H, BUTLER D H, et al. Development of a wind tunnel active vibration reduction system[C]//Proceedings of 45th AIAA Aerospace Sciences Meeting. Reno, USA: AIAA, 2007. |
| [3] |
BALAKRISHNA S, BUTLER D H, WHITE R. Active damping of sting vibrations in transonic wind tunnel testing[C]//Proceedings of 46th AIAA Aerospace Sciences Meeting. Reno, USA: AIAA, 2008.http://arc.aiaa.org/doi/abs/10.2514/6.2008-840 |
| [4] |
BALAKRISHNA S, BUTLER D H, ACHESON M J, et al. Design and performance of an active sting damper for the NASA common research model[C]//Proceedings of 49th AIAA Aerospace Sciences Meeting. Orlando, USA: AIAA, 2011.http://arc.aiaa.org/doi/abs/10.2514/6.2011-953 |
| [5] |
陈卫东, 邵敏强, 杨兴华, 等.
跨声速风洞测力模型主动减振系统的试验研究[J]. 振动工程学报, 2007, 20(1): 9l–96.
CHEN Weidong, SHAO Minqiang, YANG Xinghua, et al. Experimental evaluation of an active vibration control system for wind tunnel aerodynamic models[J]. Journal of Vibration Engineering, 2007, 20(1): 9l–96. |
| [6] |
IGOE WB, CAPONE F T. Reduction of wind tunnel model vibration by means of a tuned damped vibration absorber installed in a model[R]. NASA TMX-1606, 1968. |
| [7] |
QIU Zhicheng, ZHANG Xianmin.
Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate[J]. Journal of Sound and Vibration, 2007, 301: 521–543.
DOI:10.1016/j.jsv.2006.10.018
|
| [8] |
QIU Zhicheng, WU Hongxin, YE Chunde.
Acceleration sensors based modal identification and active vibration control of flexible smart cantilever plate[J]. Aerospace Science and Technology, 2009, 13: 277–290.
DOI:10.1016/j.ast.2009.05.003
|
| [9] |
QIU Zhicheng, HAN Jianda, ZHANG Xiamin, et al.
Active vibration control of a flexible beam using a non-collocated acceleration sensor and piezoelectric patch actuator[J]. Journal of Sound and Vibration, 2009, 326: 438–455.
DOI:10.1016/j.jsv.2009.05.034
|
| [10] |
FANSON J L, CAUGHEY T K.
Positive position feedback control for large space structure[J]. AIAA Journal, 1990, 28: 717–724.
DOI:10.2514/3.10451
|
| [11] |
杨艳丽, 张俊杰, 唐建中, 等.
一种鲁棒自适应主动振动控制方法[J]. 西安交通大学学报, 1997, 31(7): 7–11.
YANG Yanli, ZHANG Junjie, TANG Jianzhong, et al. A method of robust adaptive active vibration control[J]. Journal of Xi'an Jiaotong University, 1997, 31(7): 7–11. |
| [12] |
SONG G, SCHMIDT S P, AGRAWAL B N.
Experimental robustness study of positive position feedback control for active vibration suppression[J]. Journal of Guidance, 2001, 25(1): 179–182.
|
| [13] |
SHAN Jinjun, LIU Hongtao, SUN Dong.
Slewing and vibration control of a single-link flexible manipulator by positive position feedback (PPF)[J]. Mechatronics, 2005, 15: 487–503.
DOI:10.1016/j.mechatronics.2004.10.003
|
| [14] |
MAHMOODI S N, AHMADIAN M, INMAN D J.
Adaptive modified positive position feedback for active vibration control of structures[J]. Journal of Intelligent Material Systems and Structures, 2010, 21: 571–580.
DOI:10.1177/1045389X10361631
|
| [15] |
KIM B, WASHINGTON G N. Active vibration control of a cantilevered beam using model predictive sliding mode control[C]//Proceedings of 49th Structures, Structural Dynamics, and Material Conference. Schaumburg, USA: AIAA, 2008. |
| [16] |
马天兵, 杜菲.
基于LQR-IMCS算法的智能结构振动主动控制[J]. 华中科技大学学报, 2012, 40(3): 72–76.
MA Tianbing, DU Fei. Active vibration control of smart structure using LQR-IMCS algorithm[J]. Journal of Huazhong University, 2012, 40(3): 72–76. |
 2018, Vol. 50
2018, Vol. 50


