共轴高速直升机采用了前行桨叶概念(Advancing blade concept, ABC)旋翼,具有两副反向旋转的刚性无铰式旋翼,使得直升机桨盘两侧都存在前行桨叶,依靠前行桨叶产生部分升力从而对后行桨叶有效卸载,解决了后行桨叶失速带来的速度限制;同时结合变转速技术,解决了高速前飞时由前行边气流压缩带来的速度限制[1]。刚性旋翼的采用可使直升机布置得更紧凑,但同时上下旋翼之间间距变小,使得上下旋翼产生强烈的气动干扰,这使得对共轴高速直升机旋翼的气动分析变得复杂。
近些年,国内外一直致力于ABC旋翼的非定常气动力研究。Kim等[2-3]采用了Brown涡运输模型研究ABC旋翼的上下旋翼之间的干扰及尾迹对旋翼气动性能的影响。Lim等[4]还用自由尾迹模型,对XH-59A的ABC旋翼进行悬停性能分析。Burgess[5]就ABC旋翼在XH-59A验证机上的使用做了一个概括性的描述。国内,张银[6]针对复合式直升机较深入地开展了其干扰流场的CFD方法即飞行力学建模方法的研究,其先建立了一种适用于旋翼/推进螺旋桨/机身干扰流场的动量源数值模拟方法,同时结合动量源方法建立了一个针对复合直升机的较高精度的非线性飞行力学模型。李文浩[7]开展了复合式高速直升机共轴刚性旋翼/机身干扰流场的计算方法和模型研究,分别针对大前进比旋翼模型、共轴刚性旋翼气动特性、旋翼/机身干扰流场、高速状态桨毂阻力特性进行了数值计算。
针对ABC旋翼的气动特性计算,目前国内外主要采用的计算流体力学(Computational fluid dynamics, CFD)方法虽然精确度较高,但其模型比较复杂,耗时较长。本文从工程应用出发,使用固定尾迹模型计算旋翼的初始诱导速度分布,将其代入预定尾迹模型中进行迭代计算的方法。对于预定尾迹模型需要提供初始的尾迹几何形状,本文使用自由尾迹模型计算的单旋翼模型结果作为迭代的初始值。在此基础上,结合Leishman-Beddoes非定常动态失速模型、Pitt-Peters动态入流模型、共轴直升机上下旋翼桨叶全本征动力学方程及弹性桨叶与变距轴承边界约束条件等计算模块,建立了一种模型相对简单、实用的共轴高速直升机振动载荷计算模型。通过与实验数据对比,验证了本文所建立模型的计算精度,具有实用性。
1 共轴高速直升机旋翼振动载荷计算模型 1.1 ABC旋翼动力学边界条件图 1为ABC旋翼的结构示意图,刚体R0K0模拟桨毂刚性偏置量,内轴承K0B模拟无铰式旋翼柔性弹性轴承,ME段为桨叶翼型段。桨叶段ME在M点处的边界条件为
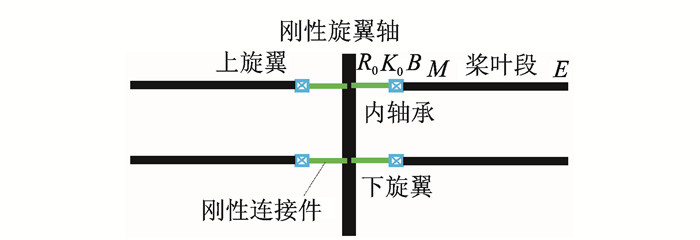
|
图 1 ABC旋翼构型 Figure 1 Configuration of ABC rotor |
| $ \begin{array}{c} \left. \begin{array}{l} {\mathit{\boldsymbol{V}}_M}-{\mathit{\boldsymbol{V}}^*} = {\bf{0}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_M}-{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^*} = {\bf{0}} \end{array} \right\} 桨叶段ME根部 \\ {\mathit{\boldsymbol{V}}^*} = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{R_0}{K_0}}} \times \left| {{\mathit{\boldsymbol{r}}_{{R_0}{K_0}}}} \right|\cdot{\mathit{\boldsymbol{A}}_1} + {{\mathit{\boldsymbol{\dot U}}}_{{K_0}B}} + {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{R_0}{K_0}}} \times {\mathit{\boldsymbol{U}}_{{K_0}B}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^*} = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{R_0}{K_0}}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}}_{{K_0}B}} \end{array} $ | (1) |
式中:UK0B及ΘK0B分别为内轴承的位移和转动自由度;A1为桨毂旋转坐标系A单位矢量[A1, A2, A3]的分量,沿着桨毂轴偏置指向变距轴承。值得注意的是,由于ABC上下旋翼是共轴反转的,因而上下旋翼的坐标转换矩阵有所不同。
1.2 共轴高速直升机旋翼全本征动力学方程以文献[8, 9]所建的无铰式单旋翼全本征动力学方程为基础,假设共轴高速直升机上下旋翼是通过刚性的旋翼轴连接,引入ABC旋翼动力学边界条件,将上下旋翼的动力学方程组合起来便得到共轴直升机的全本征动力学方程
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{A}}_{ji上}}{{\mathit{\boldsymbol{\dot q}}}_{i上}} + {\mathit{\boldsymbol{B}}_{ji上}}{\mathit{\boldsymbol{q}}_{i上}} + {\mathit{\boldsymbol{C}}_{jik上}}{\mathit{\boldsymbol{q}}_{i上}}{\mathit{\boldsymbol{q}}_{k上}} + {\mathit{\boldsymbol{D}}_{j上}} = {\bf{0}}\\ {\mathit{\boldsymbol{A}}_{ji下}}{{\mathit{\boldsymbol{\dot q}}}_{i下}} + {\mathit{\boldsymbol{B}}_{ji下}}{\mathit{\boldsymbol{q}}_{i下}} + {\mathit{\boldsymbol{C}}_{jik下}}{\mathit{\boldsymbol{q}}_{i下}}{\mathit{\boldsymbol{q}}_{k下}} + {\mathit{\boldsymbol{D}}_{j下}} = {\bf{0}} \end{array} \right. $ | (2) |
式中:A, B, C, D分别为系数矩阵;q为广义自由度(包含桨叶剖面速度及剖面载荷)。
1.3 共轴高速直升机旋翼气动力模型考虑计算的准确性以及耗时的长短,本文使用固定尾迹模型计算旋翼的初始诱导速度分布,将其代入预定尾迹模型中进行迭代计算的方法。但由于预定尾迹模型需要提供初始的尾迹几何形状,然而目前对ABC旋翼的尾迹相关研究较少,不能提供尾迹的相关数据。
本文使用自由尾迹模型计算的单旋翼模型结果作为迭代的初始值代入到预定尾迹模型中进行迭代计算。之所以不直接使用自由尾迹模型进行双旋翼迭代计算,主要出于气弹耦合迭代时间和收敛性的考虑。共轴高速直升机旋翼的气动环境较为复杂,分析难度较大,自由尾迹耗时长且难以收敛或耗散太快。
对于单个旋翼,考虑“儒氏旋翼”的情况,由毕奥-萨瓦尔定理可得位于方位角ψ的长度为Rdψ的涡线,对待求点p点诱导速度为
| $ \begin{array}{l} {V_{径}} = \frac{{- \mathit{{ {\varGamma} }}}}{{2{\mathtt{π}}Hr}}[\frac{{({R^2} + {r^2} + z_{_1}^{^2})}}{{\sqrt {{{\left( {R + r} \right)}^2} + z_{_1}^{^2}} }}\cdot\\ \;\;\;\;\;\;\;\;F\left( {\frac{{\mathtt{π}}}{2}, k} \right)-\sqrt {R + {r^2} + z_{_1}^{^2}} \cdot E\left( {\frac{{\mathtt{π}}}{2}, k} \right)]\\ {V_{轴}} = \frac{{\mathit{{ {\varGamma} }}R}}{{4{\mathtt{π}}H}}\{ I + \frac{{2\cdot{z_1}}}{{R\sqrt {\left( {R + {r^2}} \right) + z_{_1}^{^2}} }}\cdot\\ \;\;\;\;\;\;\;\;F\left( {\frac{{\mathtt{π}}}{2}, k} \right) -\frac{{\left( {{r^2} -{R^2}} \right)}}{{{{\left( {R + r} \right)}^2}}}\cdot\mathit{{ {\varPi} }}\left( {\frac{{\mathtt{π}}}{2}, n, k} \right)]\} \end{array} $ | (3) |
在实际情况下,附着涡环量是沿着桨叶半径变化的,为便于计算,将桨盘上逸出的涡系离散成有限多个涡柱(本文将其离散为5个),根据儒柯夫斯基定理与叶素理论推导并整理表达式
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{5 \times 5}}{\mathit{\boldsymbol{X}}_{5 \times 1}} = {\mathit{\boldsymbol{b}}_{5 \times 1}}\\ \mathit{\boldsymbol{X}} = {({\mathit{\varGamma}_1}, {\mathit{\varGamma}_2}, {\mathit{\varGamma}_3}, {\mathit{\varGamma}_4}, {\mathit{\varGamma}_5})^{\rm{T}}} \end{array} $ | (4) |
式中:Γi为离散的涡柱环量;其余系数矩阵的具体表达式参见文献[10],此处不予赘述。通过迭代求解式(4),可得流场中的任一点诱导速度。
共轴式双旋翼的固定涡系模型,可以简单地看成由两个单旋翼固定涡系构成。这样,整个双旋翼有2×5共10个涡柱,流场中任一点的诱导速度,都是上下两个单旋翼固定涡系中所有涡环柱诱导作用的总和。
对于初始尾迹几何形状,本文采用Johnson的自由尾迹模型[11],将尾迹几何表示为
| $ {\mathit{\boldsymbol{r}}_W}\left( {\psi, \varphi } \right) = {\mathit{\boldsymbol{r}}_b}\left( {\psi, \varphi } \right) + \varphi \mathit{\boldsymbol{\mu }} + \mathit{\boldsymbol{D}}\left( {\psi, \varphi } \right) $ | (5) |
式中:rb为桨叶上径向站点r处的位置矢量; μ是自由速度的矢量。尾迹几何的迭代过程首先需要计算所有涡元在给定涡龄φ和所有方位角ψ处的诱导速度
| $ \mathit{\boldsymbol{D}}\left( {\psi, \varphi } \right) = \mathit{\boldsymbol{D}}(\psi, \varphi-\Delta \varphi ) + \Delta \varphi \mathit{\boldsymbol{\hat q}} $ | (6) |
采用收敛性较好的伪隐式预估修正格式(Pseudo-implict predictor-corrector, PIPC)算法对其进行迭代求解,从而获得尾迹几何的稳态收敛解。
将共轴固定尾迹计算得出的桨叶各处的诱导速度值(V径及V轴)与单旋翼自由尾迹计算的尾迹几何rW(ψ, φ)代入预定尾迹模型中,作为迭代的初始值,来计算共轴双旋翼的诱导速度。
根据动量理论,考虑干扰速度, 其等于尾迹诱导速度与初始动量下洗速度之间的差值,旋翼桨叶半径为ri的一个单元产生的拉力可表示为
| $ \Delta {T_i} = \rho \left( {2{\rm{ \mathsf{ π} }}{{\bar r}_i}\Delta {r_i}} \right)\left( {{Y_i} + {w_i}} \right)2{w_i} $ | (7) |
对于叶素理论,式(7)可表示为
| $ \begin{array}{l} \Delta {T_i} = \frac{1}{2}\rho \mathit{{ {\varOmega} }} \bar r_{_i}^{^2} + {\left( {{Y_i} + {w_i}} \right)^2}b{c_i}\Delta {r_i}\cdot\\ [{C_{Li}}\cos \left( {{\beta _i} + {\varphi _i}} \right)-{C_{Di}}\sin \left( {{\beta _i} + {\varphi _i}} \right)] \end{array} $ | (8) |
涡的环量与桨叶段升力的一般关系为
| $ \rho {\mathit{\Omega }_i}\bar r{\mathit{\Gamma }_i} = \frac{1}{2}\rho {(\mathit{\Omega }{\mathit{\bar r}_i})^2}{C_{\rm{L}}}{c_i} $ | (9) |
各径向位置的升力系数
| $ \begin{array}{l} {\mathit{\Gamma }_i}- \frac{1}{2}{c_i}{\left( {\frac{{\partial {C_{\rm{L}}}}}{{\partial \alpha }}} \right)_i}{v_i} = \frac{1}{2}\mathit{\Omega }{{\mathit{\bar r}}_i}{c_i}\{ {C_{{L_i}}} + {\left( {\frac{{\partial {C_{\rm{L}}}}}{{\partial \alpha }}} \right)_i}[{\theta _R} + \\ \;\;\;\;\;\;{\theta _i}-{\alpha _i} + \tan {n_i}-\tan {\varphi _i}]\} \end{array} $ | (10) |
尾迹诱导速度为
| $ {v_i} = \sum\limits_{j = 1}^n {({\sigma _{ij + 1}}-{\sigma _{ij}}){\mathit{\Gamma }_j}} $ | (11) |
式中σij为仅与尾迹几何形状有关的影响系数。
联立式(8~11),可得
| $ \begin{array}{l} {c_i}{\left( {\frac{{\partial {C_{\rm{L}}}}}{{\partial \alpha }}} \right)_i}\sum\limits_{j = 1}^n {\left( {{\sigma _{ij + 1}}- {\sigma _{ij}}} \right)} {\mathit{\Gamma }_j} = \frac{1}{2}\mathit{\Omega }{{\mathit{\bar r}}_i}{c_i}\{ {C_{{L_i}}} + \\ {\left( {\frac{{\partial {C_{\rm{L}}}}}{{\partial \alpha }}} \right)_i}[{\theta _R} + {\theta _i}-{\alpha _i} + \tan {n_i}-\tan {\varphi _i}]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \cdots, n \end{array} $ | (12) |
注意:在计算共轴双旋翼时,某一点的环量是上下旋翼在这一点的环量相加。处理方式与固定尾迹的处理方式相同。
对于共轴预定尾迹模型计算出的上下旋翼桨叶诱导速度,采用Leishman-Beddoes非定常气动力模型来计算桨叶各剖面处的气动升力、阻力以及力矩。同时,本文用Pitt-Peters动态入流模型作为旋翼的入流模型。图 2给出了本文建立的气动力模型计算流程。
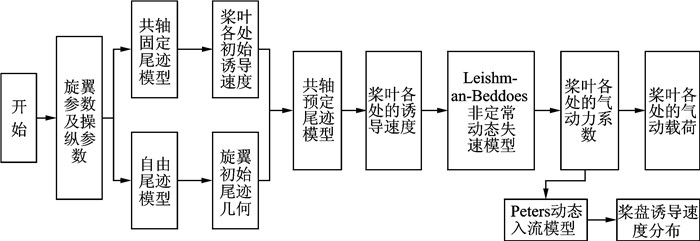
|
图 2 气动力模型计算流程 Figure 2 Calculation process of aerodynamic model |
1.4 综合方程
结合1.3节建立的动力学模型与气动力模型,得到共轴高速直升机旋翼气动弹性综合分析模型,其混合状态的空间方程可以写为
| $ \begin{array}{c} \left[{\begin{array}{*{20}{c}} {- \left[{{\mathit{\boldsymbol{C}}_{{K_0}B}}} \right]}&0&0\\ 0&{\left[{{\mathit{\boldsymbol{A}}_{ME}}} \right]}&0\\ 0&0&{\left[\mathit{\boldsymbol{M}} \right]} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot q}}}_{{K_0}B}}}\\ {{{\mathit{\boldsymbol{\dot q}}}_{ME}}}\\ {\mathit{\boldsymbol{\dot \lambda }}} \end{array}} \right] + \\ \left[{\begin{array}{*{20}{c}} {- [{\mathit{\boldsymbol{K}}_{{K_0}B}}]}&0&0\\ 0&{\left[{{\mathit{\boldsymbol{B}}_{ME}}} \right] + [\mathit{\boldsymbol{C}}({q_{ME}})]}&0\\ 0&0&{{{\left[{\mathit{\boldsymbol{\hat L}}} \right]}^{ -1}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_{{K_0}B}}}\\ {{\mathit{\boldsymbol{q}}_{ME}}}\\ \mathit{\boldsymbol{\lambda }} \end{array}} \right] = \\ \left[{\begin{array}{*{20}{c}} {-{\mathit{\boldsymbol{D}}_{{K_0}B}}(\mathit{\boldsymbol{q}}_{_{ME}}^{^{0, 1}})}\\ {-{\mathit{\boldsymbol{D}}_{ME}}\left( {\mathit{\boldsymbol{f}}, \mathit{\boldsymbol{m}}} \right)}\\ {\bf{0}} \end{array}} \right] \end{array} $ | (13) |
式中:qK0B为上下旋翼的内轴承的转动自由度;qME为上下旋翼所有桨叶段桨叶剖面速度及剖面载荷;λ为上下旋翼诱导入流系数;DME(f, m)中包含有重力以及气动载荷的贡献。
2 计算结果及分析 2.1 共轴高速直升机气动模型验证对于本文所建的共轴高速直升机气动模型,使用文献[12]中的旋翼参数进行了计算,并与实验数据进行对比。
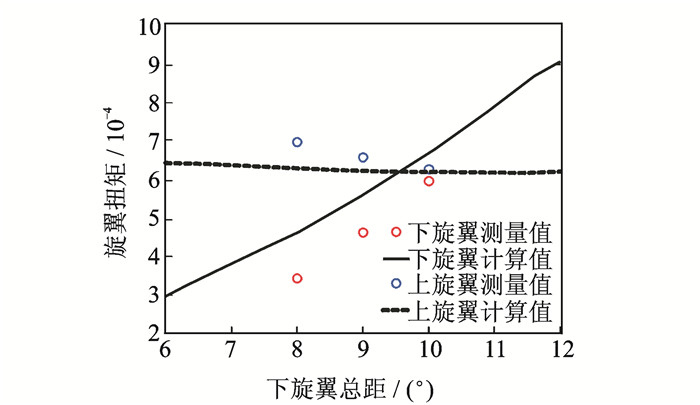
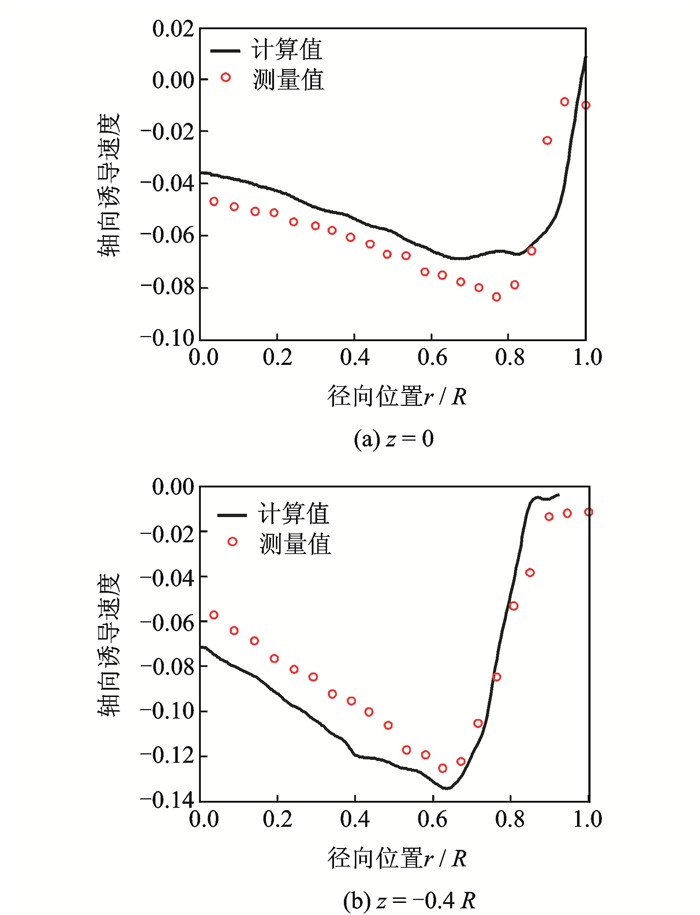
图 3,4所示为上旋翼固定总距9°不变,通过改变下旋翼的总距来研究上下旋翼的扭矩、拉力变化规律。从图中可以看出,上旋翼的扭矩、拉力都有较小的减小趋势,而下旋翼则有明显的增加,这是因为下旋翼处于上旋翼的尾流之中,上旋翼对下旋翼有较大的诱导作用。图 5为不同径向位置的轴向诱导速度及与测量值的对比。结果对比可以验证本文所建气动模型的有效性。

|
图 3 上、下旋翼拉力变化规律 Figure 3 Curves of the upper and lower rotor thrusts |
|
图 4 上、下旋翼扭矩变化规律 Figure 4 Curves of the upper and lower rotor torques |
|
图 5 共轴式旋翼诱导速度 Figure 5 Induced velocity distribution of coaxial rotors |
2.2 共轴高速直升机振动载荷计算验证
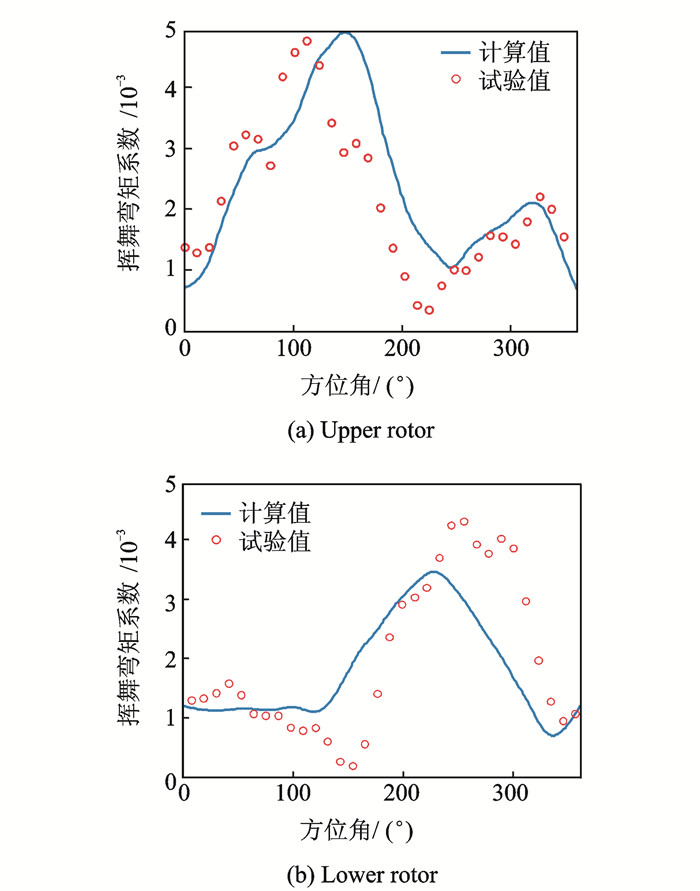
以西科斯基公司的验证机XH-59A为例,对本文所建立的共轴高速直升机旋翼载荷计算模型进行验证。文献[1]中对XH-59A上下旋翼进行了多种状态的风洞试验,本文选取中等速度与大速度前飞两个典型状态进行计算,得到了上下旋翼不同径向剖面位置的挥舞弯矩、摆振弯矩及扭矩。由于文献[1]仅测量了上下旋翼0.1R, 0.2R, 0.3R和0.6R四个剖面处的挥舞弯矩以及下旋翼0.1R一个剖面处的摆振弯矩,所以本文在计算中重点对以上剖面的振动载荷进行了对比验证。由于篇幅所限,此处仅给出了中等前飞状态(前进比为0.300 2)的振动载荷对比。
图 6~13是桨叶4个不同部位的剖面载荷计算值,从图中可以看出:

|
图 6 上、下旋翼0.1R剖面处挥舞弯矩系数 Figure 6 Flapping moment distribution of upper and lower rotors at the 0.1R section |
|
图 7 上、下旋翼0.2R剖面处挥舞弯矩系数 Figure 7 Flapping moment distribution of upper and lower rotors at the 0.2R section |

|
图 8 上、下旋翼0.3R剖面处挥舞弯矩系数 Figure 8 Flapping moment distribution of upper and lower rotors at the 0.3R section |

|
图 9 上、下旋翼0.6R剖面处挥舞弯矩系数 Figure 9 Flapping moment distribution of upper and lower rotors at the 0.6R section |

|
图 10 上、下旋翼0.1R剖面处摆振弯矩系数 Figure 10 Lagging moment distribution of upper and lower rotors at the 0.1R section |

|
图 11 上、下旋翼0.3R剖面处摆振弯矩系数 Figure 11 Lagging moment distribution of upper and lower rotors at the 0.3R section |
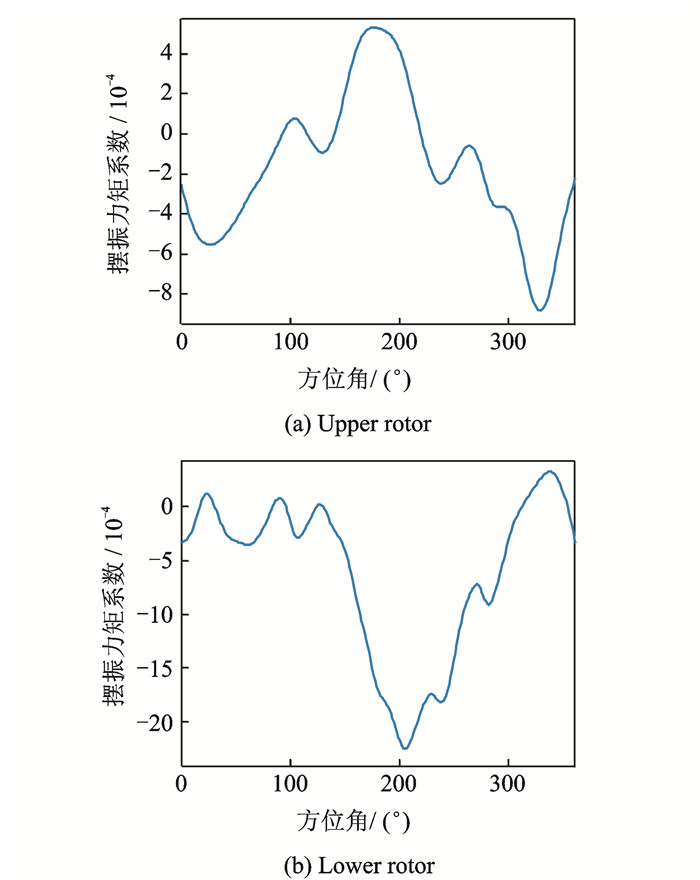
|
图 12 上、下旋翼0.6R剖面处摆振弯矩系数 Figure 12 The lagging moment distribution of upper and lower rotors at the 0.6R section |
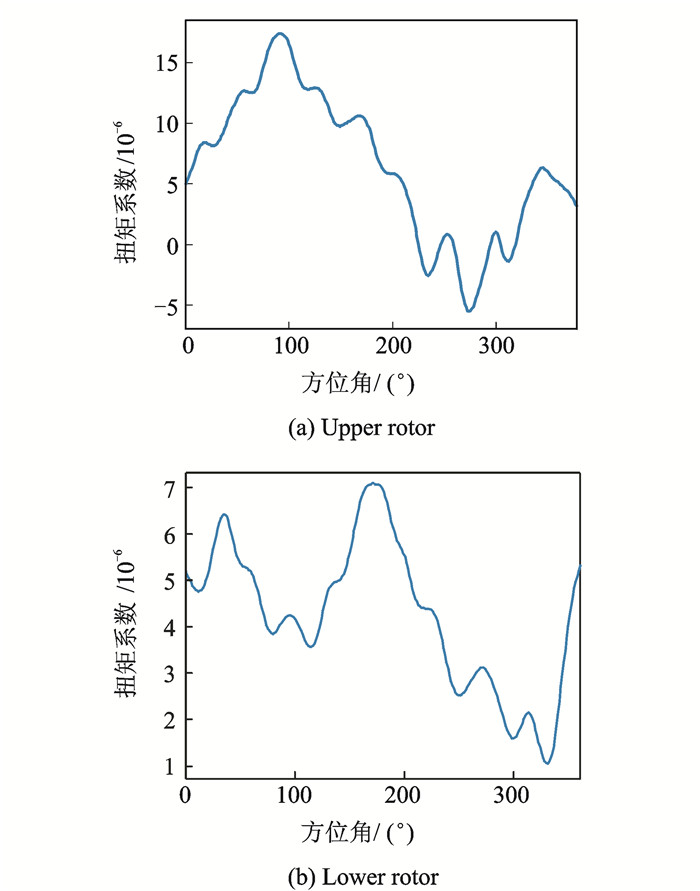
|
图 13 上、下旋翼0.6R剖面处扭矩系数 Figure 13 Pitching moment distribution of upper and lower rotors at the 0.6R section |
(1) 上下旋翼的挥舞/摆振/扭转弯矩在各个测量剖面处与实验值吻合良好,变化规律基本一致,表明本文建立的模型预测的桨叶结构载荷是有效的。
(2) 无论上下旋翼,其振动载荷随方位角的变化趋势表现出很大差异,主要表现为挥舞振动载荷在桨叶根部主要以一阶谐波为主,高频成分并不突出;在桨叶中部主要体现四阶谐波特征,而XH-59A桨叶的挥舞二阶频率为3.2,接近4 Ω,所以存在一定的动力放大效应,四阶谐波响应占主要成分。摆振振动载荷总体呈现的是一阶谐波的变化特征,这是因为挥舞运动产生的哥氏力呈现一次谐波的变化,并激励着摆振运动。桨叶的扭矩主要以一阶谐波为主,但存在许多高频成分,这可能是桨叶在旋转过程中产生了动态失速,从而造成了较大的扭转振动载荷。
(3) 越靠桨尖,挥舞/摆振振动载荷中的高频成分越大,这主要是因为桨叶外段所受到的桨涡干扰最为明显,其气动载荷随方位角的变化也最明显,同时由于上下旋翼之间存在气动干扰,这使得桨尖处的气动载荷更加复杂,从而使得振动载荷中的高频成分越大。
(4) 与上旋翼相比,在同一剖面处,下旋翼桨叶的挥舞/摆振/扭转弯矩明显小于上旋翼。由于下旋翼处于上旋翼的尾流之中,气动环境恶劣,因此产生的气动载荷要小于上旋翼产生的气动载荷,从而使得下旋翼桨叶的挥舞/摆振/扭转弯矩要小于上旋翼。
3 结束语高速直升机的研究已经成为当今国内外直升机研究的热点,其中对于ABC旋翼研究较多。本文从工程实际应用出发,重点考虑ABC构型上下旋翼之间的气动干扰,建立了适用于共轴式双旋翼的尾迹气动力模型及振动载荷计算模型。通过结果对比,验证所建计算模型具有一定的精度,为进一步开展共轴高速直升机气动弹性分析奠定了基础。
| [1] |
FELKER Ⅲ F F. Performance and loads data from a wind tunnel test of a full-scale, coaxial, hingeless rotor helicopter: NASA-TM-81329[R]. Moffett Field, California: National Aeronautics and Space Administration Moffett Field Ca Ames Research Center, 1981. |
| [2] |
KIM H W, BROWN R E. Modelling the aerodynamics of coaxial helicopters-from an isolated rotor to a complete aircraft[C]//EKC 2008 Proceedings of the EU-Korea Conference on Science and Technology. [S.l.]: Springer Berlin Heidelberg, 2008: 45-59.http://www.springerlink.com/content/kx1v44354k361152 |
| [3] |
KIM H W, BROWN R E.
A rational approach to comparing the performance of coaxial and conventional rotors[J]. Journal of the American Helicopter Society, 2010, 55(1): 12003–12003.
DOI:10.4050/JAHS.55.012003
|
| [4] |
LIM J W, MCALISTER K W, JOHNSON W.
Hover performance correlation for full-scale and model-scale coxial rotors[J]. Journal of the American Helicopter Society, 2009, 54(3): 032005–1.
DOI:10.4050/JAHS.54.032005
|
| [5] |
BURGESS R K. The ABC rotor: A historical perspective[C]//American Helicopter Society 60th Annual Forum. [S. l]: [s. n. ], 2004. |
| [6] |
张银. 复合式共轴刚性旋翼直升机气动干扰及飞行特性分析[D]. 南京: 南京航空航天大学, 2014.
|
| [7] |
李文浩. 复合式高速直升机旋翼/机身气动干扰特性的CFD分析[D]. 南京: 南京航空航天大学, 2012.
|
| [8] |
王博. 基于全本征方程的无铰式旋翼气动弹性分析方法[D]. 南京: 南京航空航天大学, 2015.
|
| [9] |
王博, 刘勇.
新型无铰式旋翼气弹综合分析的全本征方程方法[J]. 南京航空航天大学学报, 2016, 48(2): 261–267.
|
| [10] |
王平. 共轴式旋翼悬停状态气动特性研究[D]. 南京: 南京航空航天大学, 1997.
|
| [11] |
李沂霏. 共轴高速直升机旋翼气动弹性综合分析方法研究[D]. 南京: 南京航空航天大学, 2016.
|
| [12] |
JOHNSON W. Wake model for helicopter rotors in high speed flight: NASA CR 177507[R]. USA: NASA, 1988. |
 2018, Vol. 50
2018, Vol. 50


