直升机的振动一直是非常突出的问题。旋翼作为直升机的主要升力面和操纵面,是直升机主要振源之一。直升机在前飞时,旋翼的转动使桨叶经历周期性的气流环境变化,弹性桨叶在周期气动激振力作用下产生动载荷;各片桨叶动载荷合成到桨毂上形成桨毂六力素。桨叶振动载荷可以看作是由基频为1,2,3 Ω…各阶谐波分量叠加组成,对于N片桨叶的旋翼,桨毂相当于“滤波器”,只允许频率为kN Ω及(kN±1)Ω的谐波载荷通过传递到机身结构上。因此,通过降低桨叶的振动水平能够降低桨叶根部的振动载荷,从而使得直升机机身结构的激励大幅降低。
为了降低直升机振动,直升机大部分采用传统的减振吸振装置来抑制旋翼/机体振动。现如今,通过被动的吸振器和优化的动力学设计,直升机的振动水平已经从20世纪50年代的0.3~0.5g降低到0.1g左右。虽然直升机振动水平得到一定的改善,但相对于固定翼飞行器,上述振动水平还是较大,与直升机民用市场的预期振动水平和NASA提出的0.02g的目标相差较大。因此,需要一个更高效的方法来控制振动。
近二十年来,直升机振动主动控制技术日益受到重视。直升机的主动控制是通过控制系统输入能量从而来降低振动载荷。主要控制方法[1]有高阶谐波控制(Higher-order harmonic control,HHC)、独立桨叶控制(Individual blade control,IBC)、主动后缘襟翼控制和结构响应主动控制(Active control of structure response,ACSR)等。
(1) 高阶谐波控制(HHC)
高阶谐波控制采用闭环控制系统,通过监测直升机飞行时的振动反馈信号,以一定控制规律传递给与自动倾斜器不旋转环相连接的作动器产生附加的变距角,从而可以抵消振动响应中的部分或全部谐波分量。
(2) 独立桨叶控制(IBC)
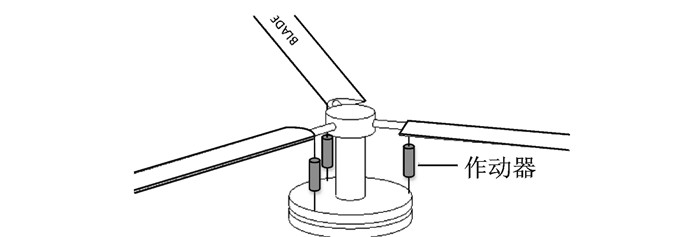
独立桨叶控制[2-3]属于高阶谐波控制的一个分支,其通过独立安装在桨叶拉杆上的作动器直接对每片桨叶单独进行高阶谐波控制(图 1)。与传统的HHC技术相比,其更具灵活性并可以补偿桨叶间的差异。
|
图 1 独立桨叶控制原理图 Figure 1 Schematic of IBC |
(3) IBC高阶谐波输入
IBC的变距输入信号表达式
| $ {\vartheta _{i, {\rm{IBC}}}} = {\vartheta _n}\cos (n{\psi _i}-{\varphi _n}) $ | (1) |
式中:ϑi, IBC为IBC的变距量,ψi为i片桨叶的方位角;则控制信号有3个参变量:幅值ϑn、谐波阶次n、相位φn;通过控制这3个变量选取合适的谐波分量加载,使得振动控制达到最优。
1 旋翼载荷模型 1.1 旋翼气动力模型定常来流下,翼型的迎角不随时间改变,升力系数随迎角是线性变化的。旋翼在周期变化的气动环境中,迎角随时间不断改变,翼型处于非定常来流状态下,所以气动力响应也是非定常的。
本文采用Leishman-Beddoes[4-6]非定常/动态失速模型,并引入动态入流模型,计算旋翼的气动响应。该气动模型对气动响应模拟主要分为以下3个部分:
(1) 附着流状态下,气动力主要由环量响应和非环量响应构成;
(2) 通过比较滞后法向力与临界法向力,判定翼型剖面气流是否发生后缘分离,计算分离点并重新校准气动力;
(3) 当后缘分离下的滞后法向力大于临界法向力时,深度失速发生,前缘涡产生并严重影响气动力值。
通过离散时间,选定时间步长,由Duhamel积分推导气动力计算公式,通过编程进行迭代计算。
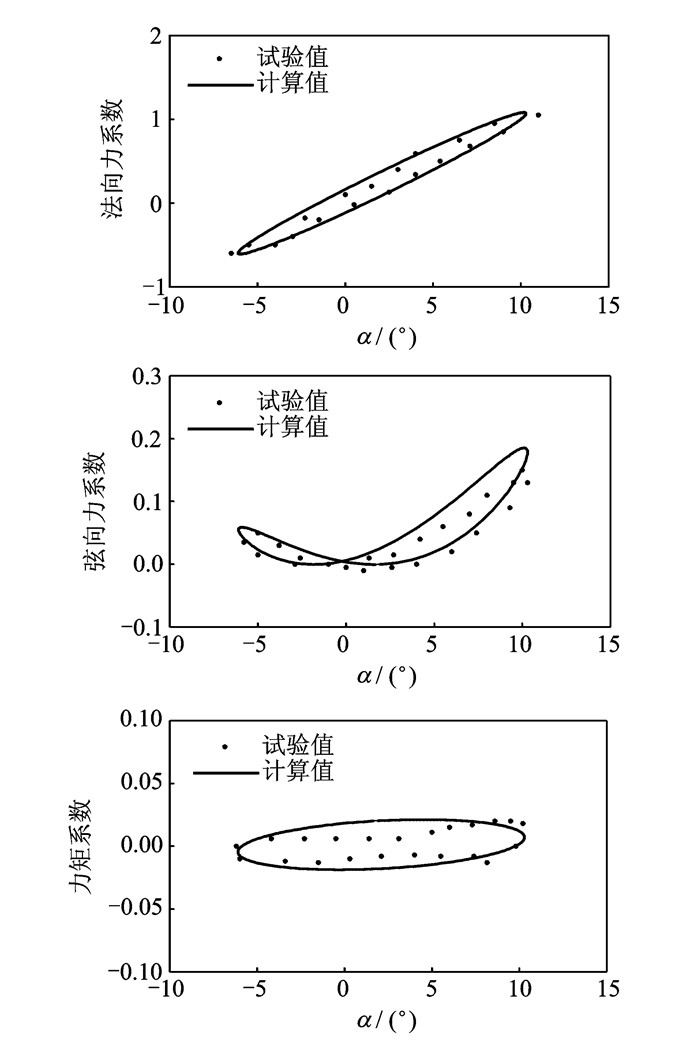
采用NACA0012翼型进行算例验证,迎角变化为α=2.1+8.2sinωt。如图 2所示,L-B气动模型计算值与试验值基本吻合。
|
图 2 L-B气动模型算例验证 Figure 2 Validation of L-B aerodynamic model |
由于直升机流场的复杂性,本文采用准确度较高、计算较精确的Pitt-Peters[7]动力入流模型。其将诱导速度表示为由桨叶展向和方位角的一阶傅里叶级数数学表达式
| $ v\left( {\bar r, \psi } \right) = {\lambda _0} + {\lambda _{1c}}\bar r{\rm{cos}}\psi + {\lambda _{1s}}\bar r{\rm{sin}}\psi $ | (2) |
式中:
旋翼总入流速度由悬停爬升速度和诱导速度叠加组成。
1.2 旋翼动力学模型本文采用动力学软件ADAMS建立旋翼系统的动力学方程。ADAMS中刚体广义坐标用直角坐标和方位角表示q=[x, y, z, ψ, θ, φ]T。
动力学计算时采用拉格朗日方程
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial T}}{{\partial {{\mathit{\boldsymbol{\dot q}}}_j}}}} \right)-\frac{{\partial T}}{{\partial {{\mathit{\boldsymbol{\dot q}}}_j}}} = {\mathit{\boldsymbol{Q}}_j} + \sum\limits_{i = 1}^n {{\lambda _i}} \frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{\partial {{\mathit{\boldsymbol{\dot q}}}_j}}} $ | (3) |
集成约束方程,建立系统的动力学方程。
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot P}}-\partial T/\partial \mathit{\boldsymbol{q + }}{\mathit{\pmb{\Phi }} ^{\rm{T}}}\lambda + {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{F = }}{\bf{0}}\\ \mathit{\boldsymbol{P}} = \partial T/\partial \mathit{\boldsymbol{\dot q}}\\ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\dot q}}\\ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{\boldsymbol{q}}, t} \right) = {\bf{0}}\\ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}, \mathit{\boldsymbol{q}}, t} \right) \end{array} \right. $ | (4) |
式中:P为广义动量;H为外加力的坐标转换矩阵。
表 1是模型旋翼的相关参数,将其导入ADAMS,建立桨叶与桨毂之间的铰接约束。将桨叶分成若干等分段,每段桨叶所受外加激励即气动载荷通过编译L-B模型的气动子程序定义加载。
| 表 1 模型旋翼参数 Table 1 Parameters of modeling rotor |
通过计算桨叶旋转状态下各阶固有模态生成MNF文件导入ADAMS,从而计算弹性桨叶的动力学方程。如图 3所示,计算前进比μ=0.14时桨毂垂向载荷。

|
图 3 μ=0.14桨毂载荷值 Figure 3 Hub load value at μ=0.14 |
2 独立桨叶控制对桨毂载荷的影响
单片桨叶控制[8-12]在输入不同阶次、幅值、相位的高阶谐波成分通过控制桨叶的桨距角来达到减振目的。桨距角可表示为
| $ \begin{array}{*{20}{c}} {\theta = {\theta _0} + {\theta _c}\cos \left( {\omega t} \right) + {\theta _s}\sin \left( {\omega t} \right) + }\\ {\begin{array}{*{20}{c}} {{A_2}{\rm{cos}}(2\omega t + {\varphi _2}) + }\\ {{A_2}{\rm{cos}}(2\omega t + {\varphi _2}) + }\\ {{A_3}{\rm{cos}}(3\omega t + {\varphi _3}) + }\\ \vdots \\ {{A_n}{\rm{cos}}(n\omega t + {\varphi _n})} \end{array}} \end{array} $ | (5) |
式中:n表示变距谐波的阶次;An为相应谐波的幅值;φn为相应谐波的相位。
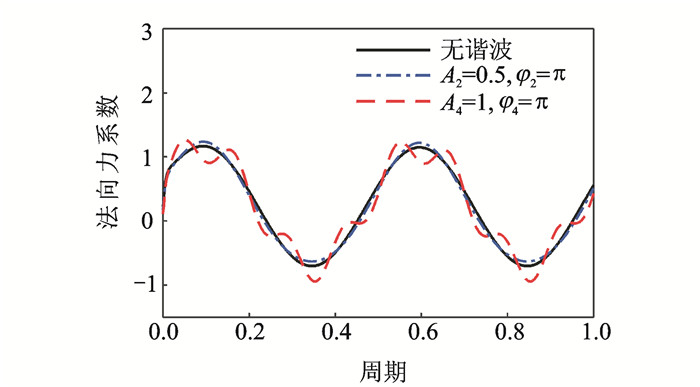
如图 4所示,在算例迎角变化基础上对二维翼型加载高阶谐波分量后,翼型的迎角会发生变化,翼型的动态气动力会随之改变,在特定谐波下,可以使得翼型某一时间范围内不进入动态失速区域。
|
图 4 谐波分量对气动力的影响 Figure 4 Effects on the aerodynamic load by the higher harmonic pitch |
为方便分析,定义桨毂载荷相对比值作为减振衡量指标。载荷比表示:某一方向上未加谐波前载荷最大值与最小值之差与加载谐波后载荷最大值和最小值之差的比值。载荷比越小,表明振动幅度越低,减振效果越好。
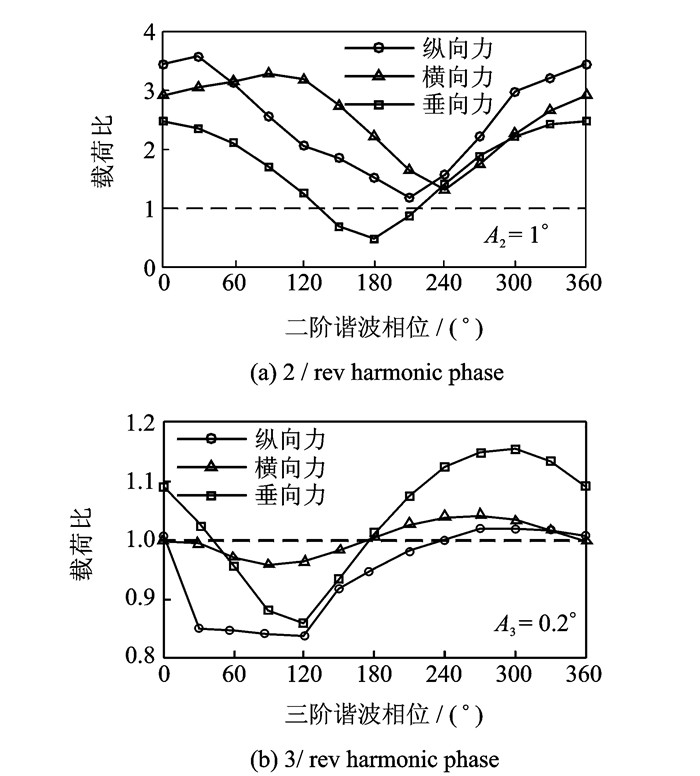
2.1 谐波相位对振动载荷的影响在前进比μ=0.14时,分别选取二阶谐波和三阶谐波独立加载到桨距上,在固定幅值不变的情况下(谐波幅值分别为A2=1,A3=0.2),改变谐波相位,绘制出载荷比变化曲线,如图 5所示。
|
图 5 谐波相位对振动载荷比的影响 Figure 5 Effects on the vibration of harmonic phase to the pitch |
由图 5可知,加载二阶谐波时,桨毂纵向、横向载荷比大于1,即二阶谐波对桨毂力只有激振作用,两方向力变化趋势相同;在谐波相位180°附近,桨毂载荷比小于1,对桨毂垂向力具有减振作用,当谐波相位处于180°时,减振效果最优。
加载三阶谐波时,谐波相位对3个方向力载荷比影响趋势相同,对桨毂纵向力与垂向力影响较大而对横向力影响十分微小。随着谐波相位增大,振动载荷比先减小后增大,垂向力由减振逐渐变为激振;当谐波相位处于120°时,减振效果最优。
对上述计算结果分析,3片桨叶旋翼系统,其桨毂垂向振动载荷主要来源于各片桨叶气动力3n阶分量(n=1, 2, 3, …)。要通过高阶谐波变距减小各方向振动,就需要谐波相位与振动载荷相位匹配,否则不仅不能达到减振目的,还会变成激振。在不同状态,不同阶次谐波达到减振效果所需要的相位不同。
2.2 谐波幅值对振动载荷的影响在前飞速度μ=0.14时,由相位影响分析,二阶谐波和三阶谐波分别选择对应的最优减振相位值(谐波相位值分别为φ2=180°,φ3=90°)。
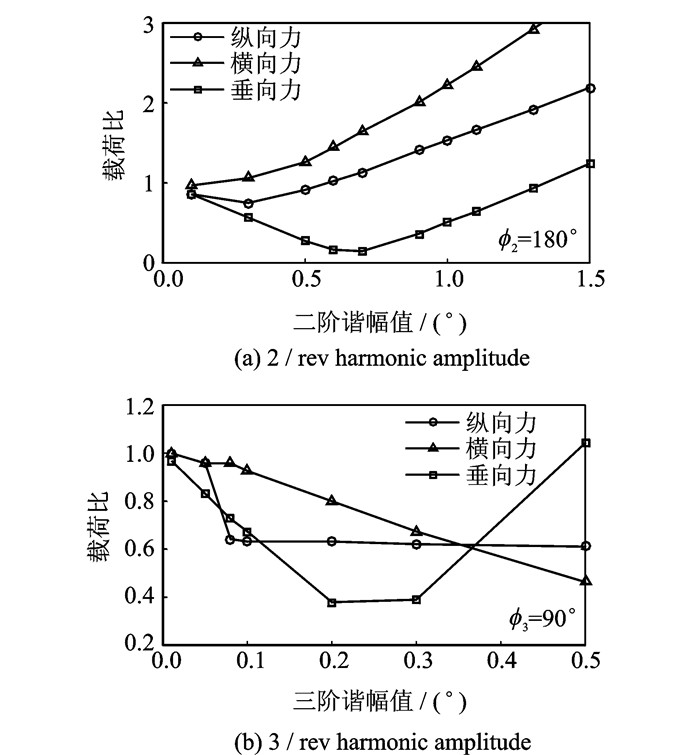
分别选取二阶谐波和三阶谐波独立加载,在固定相位不变的情况下,改变谐波幅值,绘制出载荷比变化曲线(图 6)。幅值取值从0.1°开始,每间隔0.1°增加幅值大小,计算桨毂周期内的变化量并算出载荷比,将离散数据拟合成曲线。
|
图 6 三阶谐波幅值对振动载荷比的影响 Figure 6 Effects on the vibration of harmonic amplitude to the pitch |
由图 6可知,加载二阶谐波,二阶谐波幅值较小时,对力载荷有一定的减振效果,垂向力在幅值为0.7时,减振最明显,随着谐波幅值增大,桨毂力载荷增大,会形成激振的效果。
加载三阶谐波时,能够有效降低桨毂振动载荷,垂向和纵向载荷的减振效果最为明显,侧向力在幅值为0.2左右时,减振效果最好,之后,减振逐渐转变成激振;垂向力在幅值0.8时,减振达到最优。
总体来看,谐波幅值较大时,一方面变距拉杆激励器难以实现,另一方面高阶谐波变成了振动激励,并不能达到降低振动的目的;当谐波幅值太小时,高阶谐波作用弱化,减振效果也随之减弱。
3 结论对于本文所选用的3片铰接式旋翼模型,在一定前飞状态下进行独立桨叶变距仿真,可以得出如下结论:
(1) 二阶、三阶谐波都可以大幅降低桨毂垂向振动,最大降幅能达到80%,同时对桨盘拉力影响很小。
(2) 不同阶次高阶谐波实现减振所需的谐波幅值不同,谐波幅值过小,减振效果弱,谐波幅值过大,减振转换成激振。
(3) 不同状态下独立桨叶控制对不同阶次谐波的相位需求不同,高阶谐波相位对桨毂载荷影响较大,最大振幅与最小振幅对应相位相差180°。
而对于不同旋翼模型在不同的飞行状态下,虽然其有一定的差异,但应当能够找出相应的高阶谐波阶次、幅值、相位组合加载到独立桨叶变距上,使得机体的振动水平得到降低。
| [1] |
张永孝, 李强.
直升机结构响应主动控制技术工程化应用研究[J]. 飞行力学, 2015, 33(4): 371–375.
ZHANG Yongxiao, LI Qiang. Research of engineering application for active control of helicopter structure responses[J]. Flight Dynamics, 2015, 33(4): 371–375. |
| [2] |
DAN P, LIU L, CHANDRASEKAR J, et al.
Higher-harmonic-control algorithm for helicopter vibration reduction revisited[J]. Journal of Guidance Control & Dynamics, 2012, 28(5): 918–930.
|
| [3] |
徐海, 王华明, 杨仁国.
独立桨叶高阶谐波变距对旋翼垂向载荷的影响分析[J]. 南京航空航天大学学报, 2016, 48(2): 200–204.
XU Hai, WANG Huaming, YANG Renguo. Analysis on effect of individual high harmonic blade pitch on vertical hub load[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(2): 200–204. |
| [4] |
LEISHMAN J G, BEDDOES T S.
A semi-empirical model for dynamic stall[J]. Journal of the American Helicopter Society, 1989, 34(3): 3–17.
DOI:10.4050/JAHS.34.3
|
| [5] |
宋辰瑶, 徐国华.
基于非定常气动模型的翼型动态响应计算[J]. 实验流体力学, 2005, 19(2): 28–34.
SONG Chenyao, XU Guohua. Computations of airfoil dynamic responses based on unsteady aerodynamic model[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(2): 28–34. |
| [6] |
LARSEN J W, NIELSEN S R K, KRENK S.
Dynamic stall model for wind turbine airfoils[J]. Journal of Fluids & Structures, 2007, 23(7): 959–982.
|
| [7] |
GAONKAR G, PETERS D.
Review of dynamic inflow modeling for rotorcraft flight dynamics[J]. Vertica, 1988, 12(3): 213–242.
|
| [8] |
JACKLIN S, LEYLAND J, BLAAS A, et al. Full-scale wind tunnel investigation of a helicopter individual blade control system[C]//50th Annual Forum of the AHS. USA: AIAA, 1993.http://arc.aiaa.org/doi/abs/10.2514/6.1993-1361 |
| [9] |
ARNOLD U T P, FüRST D.
Closed loop IBC results from CH-53G flight tests[J]. Aerospace Science & Technology, 2005, 9(5): 421–435.
|
| [10] |
YEO H, JAIN R, JAYARAMAN B.
Investigation of rotor vibratory loads of a UH-60A individual blade control system[J]. Journal of the American Helicopter Society, 2011, 56(4): 1–18.
|
| [11] |
JACKLIN S A, HABER A, SIMONE G D, et al. Full-scale wind tunnel test of an individual blade control system for a UH-60 helicopter[C]//AHS 58th Annual Forum. Montreal, Canada: American Helicopter Society Inernational, 2002. |
| [12] |
RAVICHANDRAN K, CHOPRA I, WAKE B E, et al.
Trailing-edge flaps for rotor performance enhancement and vibration reduction[J]. Journal of the American Helicopter Society, 2013, 58(2): 1–13.
|
 2018, Vol. 50
2018, Vol. 50


