直升机在飞行过程中会受到来自旋翼的交变载荷,使机体产生非常严重的振动问题。隔振法是振动传递途径控制的常用方法,通过隔断振动传递达到减振的目的,结构简单、成本低、可靠性高且有着较好的控制效果。国内外应用液弹隔振器[1]、节点梁隔振[2]和聚焦隔振[3]等设计措施进行了隔振研究,并应用于直升机隔振[4]。传统的被动隔振系统结构简单、易于实现、经济性好、可靠性高且不额外消耗能量,但被动隔振存在固有缺陷,限制了隔振性能的提高。与被动隔振相比,主动隔振具有适应性强、低频隔振效果好以及质量轻等优点,因而能够更有效地应用于直升机隔振[5-6]。在主减撑杆处进行主动隔振能够有效地降低振动水平[7-8]。压电叠层作动器由于质量轻、响应快和效率高等优点,已在直升机振动主动控制中受到高度重视[9-12]。本文采用安装在主减斜撑杆上的压电叠层作动器建立了直升机主动隔振系统。基于压电材料本构关系推导了压电叠层作动器的驱动方程,建立了压电叠层作动器驱动的主减主动隔振系统动力学模型。采用了自适应滤波控制方法,通过最小均方算法实现了自适应控制。进行了直升机主动隔振仿真,表明该系统具有高效的隔振效果。
1 主动隔振系统建模有效可靠的动力学模型是设计主动隔振系统的基础。本文将压电叠层作动器并联在撑杆处隔振旋翼激励,建立压电叠层作动器与系统的动力学模型是结构控制设计的前提条件[13]。
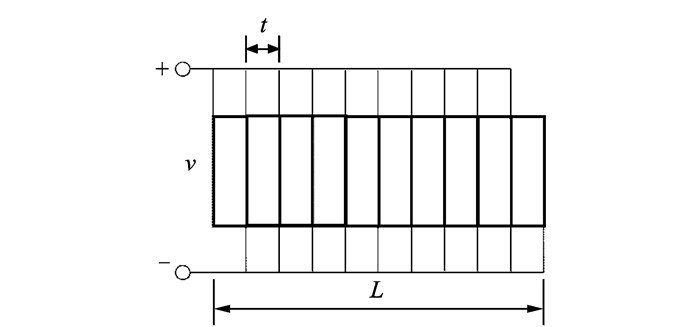
1.1 压电叠层作动器压电材料由于具有逆压电效应,当给压电材料施加电场时会使压电材料内部的正负电荷中心发生相对移动,导致压电材料产生机械变形。其变形与外加电场成比例关系,所以给压电材料施加一定的电场强度,就可以使压电材料按照预设的规律变形,从而具有驱动能力,可以作为驱动元件应用于控制。压电作动器优良的性能,使其越来越多地用于振动主动控制。压电叠层作动器模型如图 1所示,其中L为压电叠层作动器的长度,v为施加在每个压电片上的电压,t为压电片厚度。忽略各层压电片的电极和粘结层的影响,压电叠层作动器可以看作是由压电片机械串联构成的[14]。
|
图 1 压电叠层作动器模型图 Figure 1 Piezoelectric stack actuator model diagram |
图 1中可以看出,在压电叠层作动器中,电场和产生的驱动力都在作动器的轴向。因此把压电叠层作动器简化成一维杆件,则其一维本构方程为
| $ {\sigma _3} = - {e_{33}}{E_3} + s_{33}^E{\varepsilon _3} $ | (1) |
式中:σ3和ε3为压电叠层作动器的轴向应力和应变,下标“3”表示压电材料的极化方向,E3为电场强度。根据压电片电学并联的特点,电场强度为E3=v/t。
将作动器理想化成一个杆单元,建立一维杆单元有限元模型。根据应变能与虚功原理,得到外力Fac, 杆两端位移u1,u2与外加电压v为
| $ {\mathit{\boldsymbol{F}}_{{\rm{ac}}}} = \frac{{s_{33}^E{A_0}}}{L}\left[ {\begin{array}{*{20}{c}} 1&{ - 1}\\ { - 1}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}} \end{array}} \right] - \frac{{{e_{33}}{A_0}}}{t}\left[ {\begin{array}{*{20}{c}} 1\\ { - 1} \end{array}} \right] $ | (2) |
位移差Δu=u1-u2,则可写为
| $ {\mathit{\boldsymbol{F}}_{{\rm{ac}}}} = {k_{{\rm{ac}}}}\Delta u + {k_v}v $ | (3) |
式中:
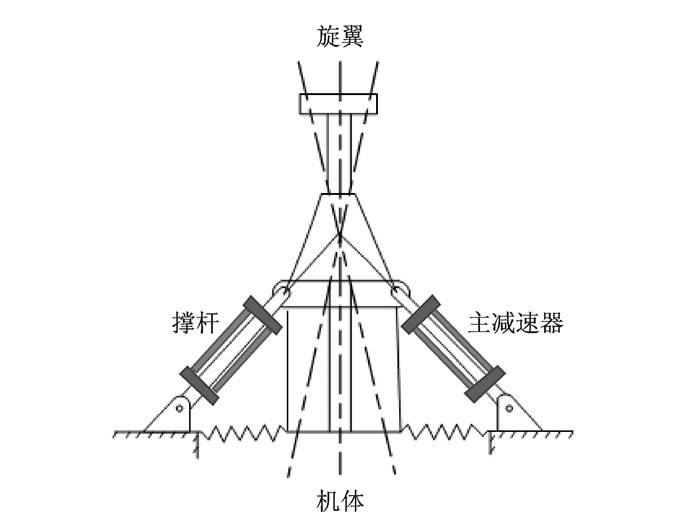
本文采用的主动隔振系统的平面图如图 2所示,用2根撑杆连接主减速器与机身,撑杆轴线交于瞬心,使主减速器能绕瞬心在平面内转动,由于撑杆轴向刚度很大,通过减速器底部的弹性基座,使旋翼与减速器的固有频率低于旋翼通过频率,实现振动隔离。压电叠层作动器与撑杆并联连接,组成主减主动隔振系统。为避免压电叠层作动器承受过大拉力,连接时在作动器两端预加合适的预紧力。
|
图 2 主动隔振系统示意图 Figure 2 Illustration of active vibration isolation system |
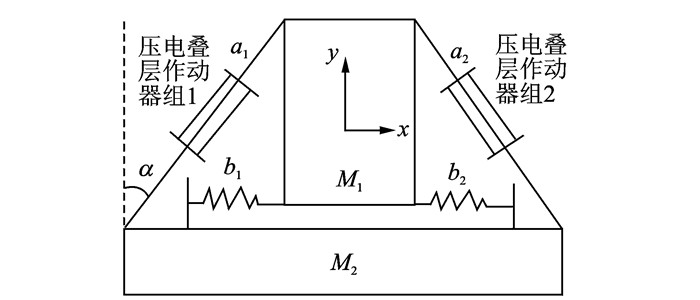
将图 2中的隔振系统模型简化成图 3,其中:M1为主减速器质量;M2为机身质量;α为撑杆与垂向的夹角,也是压电叠层作动器的安装角;a1, a2为两根并联入压电叠层作动器的撑杆;b1, b2为提供转动刚度的弹簧。旋翼激励分别为x方向Fx,y方向Fy,作用点为主减速器质心;kb为弹簧刚度;v1, v2为两作动器的控制电压。
|
图 3 主动隔振系统模型 Figure 3 Active vibration isolation system model |
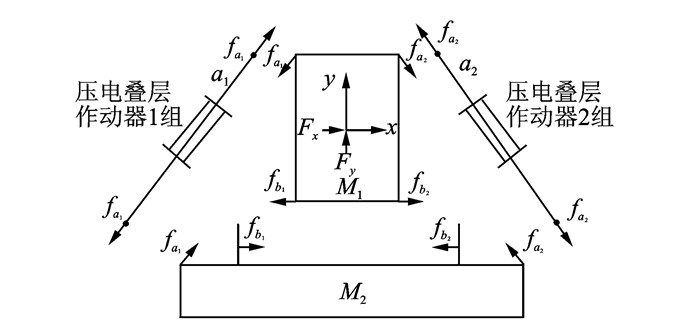
如图 4所示,在平面内,水平方向x向右为正,垂直方向y向上为正,转动方向θ逆时针为正,对主动隔振系统进行受力分析。
|
图 4 主动隔振系统受力分析图 Figure 4 Analysis diagram of active vibration isolation system |
加装了压电叠层作动器的撑杆所受外力、变形与外加电压的关系为
| $ {\mathit{\boldsymbol{f}}_a} = {k_a}\Delta u + {k_v}v $ | (4) |
式中:ka为撑杆与压电叠层作动器的总轴向刚度。
根据受力分析列出主减速器与机身的动力学方程。主减速器M1为
| $ {M_1}{{\ddot x}_1} = {F_x} - {f_{{a_1}}}\cos \alpha + {f_{{a_2}}}\cos \alpha - {f_{{b_1}}} + {f_{{b_2}}} $ | (5) |
| $ {M_1}{{\ddot y}_1} = {F_y} - {f_{{a_1}}}\sin \alpha - {f_{{a_2}}}\sin \alpha $ | (6) |
| $ \begin{array}{*{20}{c}} {{J_1}{{\ddot \theta }_1} = n{f_{{a_1}}}\cos \alpha - n{f_{{a_2}}}\cos \alpha - n{f_{{b_1}}} + }\\ {n{f_{{b_2}}} + m{f_{{a_1}}}\sin \alpha - m{f_{{a_2}}}\sin \alpha } \end{array} $ | (7) |
机身M2为
| $ {M_2}{{\ddot x}_2} = {f_{{a_1}}}\cos \alpha - {f_{{a_2}}}\cos \alpha + {f_{{b_1}}} - {f_{{b_2}}} $ | (8) |
| $ {M_2}{{\ddot y}_2} = {f_{{a_1}}}\sin \alpha + {f_{{a_2}}}\sin \alpha $ | (9) |
| $ \begin{array}{*{20}{c}} {{J_2}{{\ddot \theta }_2} = - d{f_{{a_1}}}\cos \alpha + d{f_{{a_2}}}\cos \alpha - d{f_{{b_1}}} + }\\ {d{f_{{b_2}}} - l{f_{{a_1}}}\sin \alpha + l{f_{{a_2}}}\sin \alpha } \end{array} $ | (10) |
整理式(5~10),得到动力学方程的矩阵形式为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{M_1}}&0&0&0&0&0\\ 0&{{M_1}}&0&0&0&0\\ 0&0&{{J_1}}&0&0&0\\ 0&0&0&{{M_2}}&0&0\\ 0&0&0&0&{{M_2}}&0\\ 0&0&0&0&0&{{J_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot x}_1}}\\ {{{\ddot y}_1}}\\ {{{\ddot \theta }_1}}\\ {{{\ddot x}_2}}\\ {{{\ddot y}_2}}\\ {{{\ddot \theta }_2}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{K_{11}}}&{{K_{21}}}&{{K_{31}}}&{{K_{41}}}&{{K_{51}}}&{{K_{61}}}\\ {{K_{21}}}&{{K_{22}}}&{{K_{21}}}&{{K_{42}}}&{{K_{52}}}&{{K_{62}}}\\ {{K_{31}}}&{{K_{32}}}&{{K_{33}}}&{{K_{43}}}&{{K_{53}}}&{{K_{63}}}\\ {{K_{41}}}&{{K_{42}}}&{{K_{43}}}&{{K_{44}}}&{{K_{54}}}&{{K_{64}}}\\ {{K_{51}}}&{{K_{52}}}&{{K_{53}}}&{{K_{54}}}&{{K_{55}}}&{{K_{65}}}\\ {{K_{61}}}&{{K_{62}}}&{{K_{63}}}&{{K_{64}}}&{{K_{65}}}&{{K_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{y_1}}\\ {{\theta _1}}\\ {{x_2}}\\ {{y_2}}\\ {{\theta _2}} \end{array}} \right] = \mathit{\boldsymbol{f}}} \end{array} $ | (11) |
式中
| $ {K_{11}} = {K_{44}} = 2{k_a}{\cos ^2}\alpha + 2{k_b} $ |
| $ {K_{22}} = {K_{55}} = 2{k_a}{\sin ^2}\alpha $ |
| $ {K_{31}} = - 2r{k_a}\cos \alpha + 2n{k_b} $ |
| $ {K_{33}} = 2{r^2}{k_a} + 2{n^2}{k_b} $ |
| $ {K_{41}} = - 2{k_a}{\cos ^2}\alpha - 2{k_b} $ |
| $ {K_{43}} = 2r{k_a}\cos \alpha - 2n{k_b} $ |
| $ {K_{52}} = - 2{k_a}{\sin ^2}\alpha $ |
| $ {K_{61}} = 2s{k_a}\cos \alpha + 2d{k_b} $ |
| $ {K_{63}} = - 2rs{k_a} + 2nd{k_b} $ |
| $ {K_{64}} = - 2s{k_a}\cos \alpha - 2d{k_b} $ |
| $ {K_{66}} = 2{s^2}{k_a} + 2{d^2}{k_b} $ |
| $ \boldsymbol{f} = \left[ {\begin{array}{*{20}{c}} {{F_x} - {k_v}\left( {{v_1} - {v_2}} \right)\cos \alpha }\\ {{F_y} - {k_v}\left( {{v_1} + {v_2}} \right)\sin \alpha }\\ {r{k_v}\left( {{v_1} - {v_2}} \right)}\\ {{k_v}\left( {{v_1} - {v_2}} \right)\cos \alpha }\\ {{k_v}\left( {{v_1} + {v_2}} \right)\sin \alpha }\\ {s{k_v}\left( {{v_2} - {v_1}} \right)} \end{array}} \right] $ |
式中:r=ncosα+msinα,s=dcosα+lsinα,刚度矩阵K中的其余项均为0。
2 主动控制方法对于主动隔振系统,由于系统工作在持续激励下,如果能够采集到与振源信号相关的参考信号,那么就可以采用前馈控制。自适应前馈控制能够抵消前馈信号对被控对象的振动干扰。本文采用最小均方算法(Least mean square, LMS)进行了自适应前馈控制。
2.1 状态方程对得到的主动隔振系统动力学方程加上模态阻尼,得到的振动方程为
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{C\dot X}} + \mathit{\boldsymbol{KX}} = {\mathit{\boldsymbol{f}}_e} + {\mathit{\boldsymbol{f}}_v} $ | (12) |
式中:M, C, K分别为质量、阻尼和刚度矩阵,X为位移向量,fe, fv分别为激振力向量与控制力向量。
对方程进行解耦与模态正交化,得到模态方程为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{M \boldsymbol{\varPhi} \ddot q}} + 2\zeta {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}_n}\mathit{\boldsymbol{ \boldsymbol{\varPhi} \dot q}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{M \boldsymbol{\varPhi} q}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{Ew}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}} $ | (13) |
式中:E为激励位置矩阵,D为作动器机电转换矩阵,ζ为系统的阻尼比,Φ为系统的特征向量矩阵,已对特征向量矩阵进行模态截断,只保留振动模态向量。
将运动方程改写为状态空间下的控制系统方程,设状态量为
| $ \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{q}}\\ {\mathit{\boldsymbol{\dot q}}} \end{array}} \right] $ | (14) |
得到状态方程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{ \dot x}} = \mathit{\boldsymbol{Ax}} + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{B}}_2}v\\ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{C}}_1}\mathit{\boldsymbol{x}} \end{array} \right. $ | (15) |
式中
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\pmb{0}}&\mathit{\boldsymbol{I}}\\ { - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{M \boldsymbol{\varPhi} }}}&{ - 2\zeta {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}_n}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} \mathit{\pmb{0}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{E}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} \mathit{\pmb{0}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{D}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{C}}_1} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{E}}_{{\rm{out}}}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}&\mathit{\pmb{0}} \end{array}} \right] $ |
其中Eout为输出位置矩阵。
2.2 自适应滤波算法自适应滤波算法的基本目标是利用前一时刻获得的滤波器参数等结果,自动调整当前时刻的滤波器参数,使滤波器输出尽可能使包含参考信号的某个特定目标函数最小化。自适应滤波具有很强的自学习、自跟踪能力,适用于平稳和非平稳随机信号的检测和估计。最小化算法是自适应算法的基本要素之一。最小化算法会从本质上对自适应过程的收敛速度和计算复杂程度产生影响。常用的优化方法有牛顿方法、最陡下降方法等。
图 5给出自适应滤波的一般结构。通常选取误差信号构造滤波器权系数更新的性能函数,通过目标函数最小化使自适应滤波器的输出信号与期望信号相匹配。为了适用于实时控制,通过对目标函数进行修改,采用瞬时误差的平方代替均方误差,以瞬时误差信号平方的梯度作为均方误差函数梯度的估计,简化梯度向量。LMS由于计算简单,在平稳环境中易于收敛等特性,成为自适应滤波理论中应用最广泛的算法。

|
图 5 自适应滤波的一般结构 Figure 5 General structure of adaptive filtering |
使用LMS算法的滤波器权系数更新方程为
| $ \mathit{\boldsymbol{e}}\left( n \right) = \mathit{\boldsymbol{d}}\left( n \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{w}}\left( n \right) $ | (16) |
| $ \mathit{\boldsymbol{w}}\left( {n + 1} \right) = \mathit{\boldsymbol{w}}\left( n \right) + 2\mu \mathit{\boldsymbol{e}}\left( n \right)\mathit{\boldsymbol{x}}\left( n \right) $ | (17) |
| $ \mathit{\boldsymbol{y}}\left( n \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{x}}\left( n \right) $ | (18) |
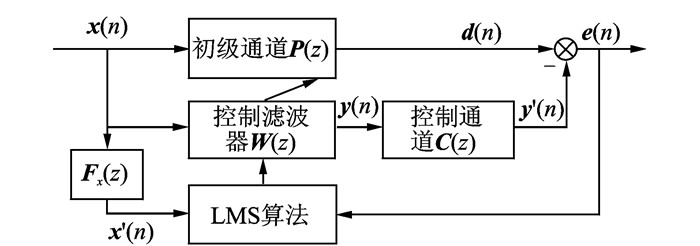
自适应前馈控制系统(图 6)依靠有限脉冲响应(Finite impulse response,FIR)滤波器实现,基于LMS算法实现权系数矢量的实时更新,调整自适应滤波器的输出,生成的前馈信号经过驱动器转化为控制力,该作用力生成与激励响应相抵消的响应,从而隔离外激励对机身的振动。
|
图 6 自适应前馈控制示意图 Figure 6 Adaptive feedforward control diagram |
在实际应用中自适应控制的输出要经过次级通道才能与机身上的旋翼激励响应相互抵消,由于次级通道的存在,传统LMS算法会引入控制误差,影响控制系统的收敛精度和稳定性,对隔振性能和隔振效果都有影响。
为了消除次级通道对自适应控制过程带来的影响,可以在参考信号和自适应滤波器之间引入次级通道模型的估计Fx(z),对滤波器的输入进行修正,得到所对应的权函数。
初级通道与控制通道均可由状态空间得到,关键在于如何估计Fx(z)。当不能确定控制通道模型时通常采用实验方法对Fx(z)进行辨识。以x方向激励输入到第1个作动器控制电压的控制过程为例,控制通道可由状态空间表示,这里采用状态空间中x方向激励输入到第1个作动器控制电压的传递函数来表示Fx(z)。
以此类推,分别用多个激励输入与多个控制电压的对应传递函数表示Fx(z)。由此得到每个输入到每个控制电压的控制通道,将不同激励输入生成的同一作动器的控制电压叠加,得到每个作动器的总控制电压。
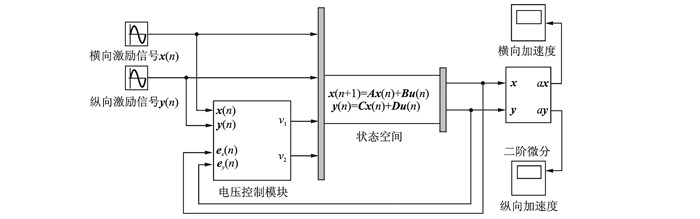
3 主动控制仿真 3.1 时域仿真系统根据自适应滤波的振动主动控制系统的结构框图搭建Simulink仿真模型。如图 7所示,系统输入信号包含x方向与y方向激励信号以及通过电压控制模块得到的控制电压信号,系统输出信号为x方向与y方向加速度,状态空间模块用来描述控制系统的数学模型,即式(15)所表示的状态空间方程。
|
图 7 Simulink仿真总模型 Figure 7 Simulink simulation model |
在电压控制模块中,选择对应的传递函数来表示Fx(z),基于LMS算法可以分别得到每个输入信号对每个作动器作用产生的电压。将同一作动器的电压叠加计算出压电叠层作动器的控制电压。
3.2 仿真结果与分析利用基于LMS自适应控制算法的控制系统仿真模型,对隔振系统的振动主动控制进行了时域仿真,验证控制系统对稳态振动的控制效果。
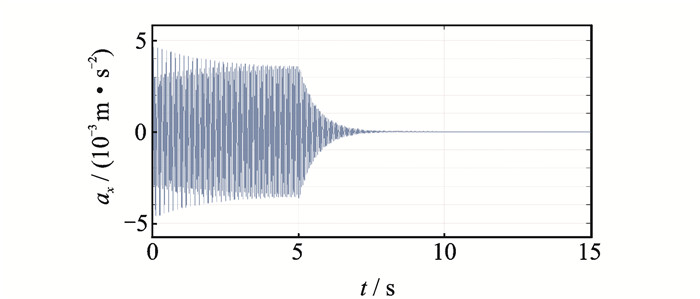
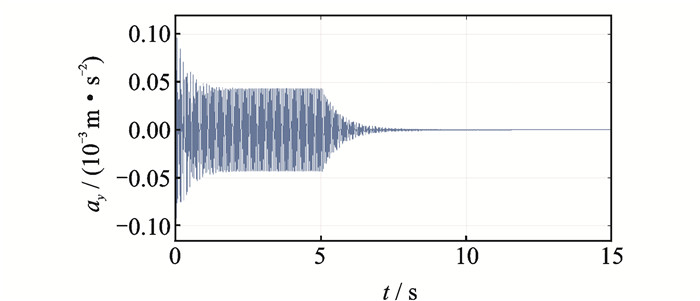
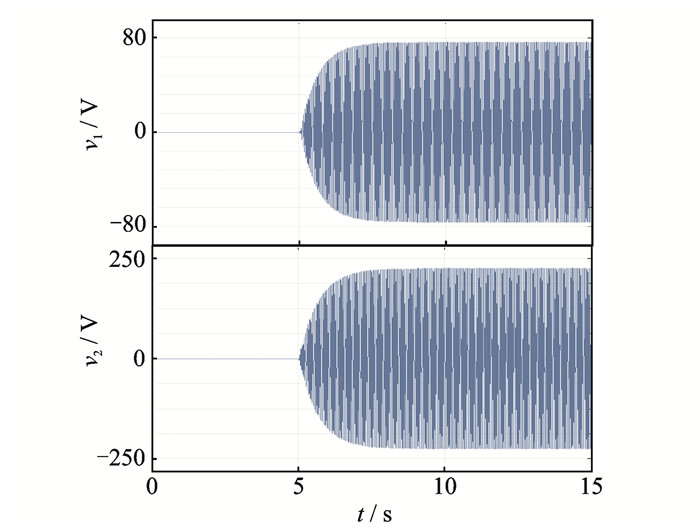
系统参数如下:主减质量M1=150 kg,机身质量M2=2 000 kg,斜撑杆长度为L=0.8 m,轴向刚度为ka=7.5×106 N/m。压电叠层作动器型号为PSt500/10/40VS18,参数如表 1所示。当系统无控制输入时得到机身的振动响应,以此作为衡量振动控制效果的参考值。x方向激振力幅值为100 N,y方向激振力幅值1 000 N,频率均为19.2 Hz,激振力从0 s开始作用,当机身在激振力作用下进入稳态,在5 s时施加控制信号,对振动进行控制,得到加入控制后的x方向与y方向振动响应如图 8,9所示,两个压电叠层作动器的控制电压如图 10所示。
| 表 1 PSt500/10/40VS18型压电叠层作动器参数 Table 1 PSt500/10/40VS18 piezoelectric stack actuator parameters |
|
图 8 加入控制后的机身x方向振动响应 Figure 8 Vibration response in x direction with control |
|
图 9 加入控制后的机身y方向振动响应 Figure 9 Vibration response in y direction with control |
|
图 10 两个压电叠层作动器的控制电压 Figure 10 Control voltage of two piezoelectric stack actuators |
从仿真结果可以看出,系统受控后,机身x方向上振动加速度降低了99%以上,y方向上振动加速度降低了98%以上。说明该系统具有良好的振动抑制效果。系统重新回到稳态消耗的时间约为2 s,具有比较好的响应速度。
4 结束语本文对在主减速器斜撑杆上安装压电叠层作动器的直升机主动隔振进行了研究。建立了压电叠层作动器与主减隔振系统耦合动力学模型。采用
自适应滤波器,通过LMS自适应算法对主减隔振系统进行了前馈控制,通过引入Fx(z)模块消除次级通道的影响。在Simulink中对主动隔振系统进行了控制仿真。仿真结果表明,系统能够在短时间内产生显著的振动抑制效果。
| [1] |
FLANNELEY W G. The dynamic anti-resonant vibration isolator[C]//American Helicopter Society 22th Annual Forum. Washington, Americam: Klelicoptar Society, 1966: 153-158. |
| [2] |
GAFFEY T M, BALKE R W. Isolation of rotor induced vibration with the bell focal pylon-nodal beam system[C]//Aerospace Engineering and Manufacturing Meeting. San Diego: [s.n.], 1976: 1-10.http://papers.sae.org/760892/ |
| [3] |
BALKE R W. Development of the kinematic focal isolation system for helicopter rotors[C]//38th Shock and Vibration Symposium. St Louis: [s.n.], 1968: 263-283. |
| [4] |
SZEFI J T. Helicopter gearbox isolation using periodically layered fluidic isolators[D]. Pennsylvania State: Pennsylvania State University, 2003.http://adsabs.harvard.edu/abs/2003PhDT.......218S |
| [5] |
宋来收, 夏品奇.
直升机振动主动控制的机身/压电叠层作动器耦合优化法[J]. 航空学报, 2011, 32(10): 1835–1841.
SONG Laishou, XIA Pinqi. Coupled fuselage/piezoelectric stack actuator optimization method for active vibration control of helicopter[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1835–1841. |
| [6] |
SCHOULZ G.
Active multivariable vibration isolation for a helicopter[J]. Automatica, 1979, 15: 461–466.
DOI:10.1016/0005-1098(79)90020-7
|
| [7] |
SUTTON T J ELLIOTT S J.
Active isolation of multiple stractural waves on a helicopter gearbox support strut[J]. Journal of Sound and Vibration, 1997, 205(1): 81–101.
DOI:10.1006/jsvi.1997.0972
|
| [8] |
GUAN Y H, LIM T C.
Experimental study on active vibration control of a gearbox system[J]. Journal of Sound and Vibration, 2005, 282: 713–733.
DOI:10.1016/j.jsv.2004.03.043
|
| [9] |
SONG Laishou, XIA Pinqi.
A harmonic synchronous identification-updating method for active control of helicopter structural response driven by piezoelectric stack actuators[J]. Journal of the American Helicopter Society, 2015, 60(3): 032013-1–032013-14.
|
| [10] |
SONG Laishou, XIA Pinqi.
Active vibration control by harmonic input compensation for piezoelectric stack actuator nonlinearity[J]. AIAA Journal of Aircraft, 2014, 51(6): 2027–2031.
DOI:10.2514/1.C032752
|
| [11] |
SONG Laishou, XIA Pinqi.
Active control of helicopter structural response using piezoelectric stack actuators[J]. AIAA Journal of Aircraft, 2013, 50(2): 659–663.
DOI:10.2514/1.C031758
|
| [12] |
孟德. 压电叠层作动器驱动的直升机框架结构振动主动控制[D]. 南京: 南京航空航天大学, 2014.
MENG De. Active vibration control of helicopter frame structure driven by piezoelectric stack actuators[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D565391 |
| [13] |
李双. 压电智能结构主动隔振系统研究[D]. 西安: 西北工业大学, 2004.
LI Shuang. Study on active isolation system of piezoelectric intelligent structure[D]. Xi'an: Northwestern Polytechnical University, 2004.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y585462 |
| [14] |
宋来收. 压电叠层作动器驱动的直升机结构响应自适应控制[D]. 南京: 南京航空航天大学, 2013.
SONG Laishou. Adaptive control of helicopter structural response driven by piezoelectric stack actuators[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D565208 |
 2018, Vol. 50
2018, Vol. 50


