2. 陆军航空兵军事代表局驻哈尔滨地区军事代表室, 哈尔滨, 150066
2. The Military Representative Office of the Army Aviation Department in Harbin Region, Harbin, 150066, China
提升直升机旋翼性能一直是直升机领域研究中的重点之一,桨叶上加装格尼襟翼可有效改善翼型气动特性[1-3]。格尼襟翼是一块沿着垂直翼型弦线的方向安装于翼型尾缘或接近尾缘的平板,具有增升显著、构造简单以及可靠性高等优点,但其驱动机构需要满足紧凑高效的要求[4]。
国内外学者针对其不同的驱动机构进行了广泛的研究。文献[5]设计了一种利用桨叶离心力产生的压差驱动格尼襟翼的方案,改善了格尼襟翼的稳定性和优化了翼型后缘结构。文献[6]设计了一套以音圈为驱动元件的驱动系统,能够提供足够的位移和驱动力。文献[7]利用压电悬臂梁驱动格尼襟翼,在18.5 Hz频率下格尼襟翼的最大位移达到0.8英寸。压电悬臂梁是压电材料应用最常见的结构形式,其具有低功耗、结构简单、无电磁干扰和变形量可观等特点[8]。文献[9]采用有限元分析方法,分析了压电双晶片悬臂梁的位移形变特征并测试了压电双晶片的振动特性,为压电双晶片结构的优化设计提供了依据。程光明等[10]探讨了悬臂式压电双晶片振子的夹持长度的变化对其动态特性的影响规律。
图 1是用于驱动格尼襟翼的压电悬臂梁的示意图。为了研究用于驱动格尼襟翼的压电悬臂梁的位移,本文采用Euler-Bernoulli梁模型和有限元法对压电悬臂梁结构的静力特性进行分析,探究基体厚度、压电片布置距离等参数对自由端位移的影响,为格尼襟翼驱动机构的设计和应用提供参考。
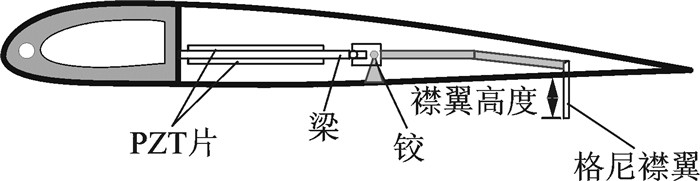
|
图 1 格尼襟翼驱动机构 Figure 1 Drive mechanism of gurney flap |
1 压电悬臂梁的基本方程
压电材料具有正、逆压电效应,广泛应用于振动和噪声控制、损伤检测等领域。将压电材料薄膜粘贴在结构表面或嵌入结构内部形成压电结构[11]。目前,压电悬臂梁结构大多是将压电片对称粘贴在悬臂梁的表面,如图 2所示。上下两层为压电层,中间为基体层,基体是各向同性的弹性材料。

|
图 2 压电悬臂梁 Figure 2 Piezoelectric cantilever beam |
1.1 压电方程
用于压电悬臂梁结构中的压电材料是一种驱动元件,电场是输入,而机械应变是输出[12]。其本构关系(忽略温度变化的影响)如下
| $ \varepsilon = \mathit{\boldsymbol{s}}\sigma + {\mathit{\boldsymbol{d}}^{\rm{T}}}E $ | (1) |
式中:ε,σ和E分别表示应变、应力和电场强度;s,d分别表示柔度系数矩阵和压电应变系数矩阵。等式右边第1项是弹性应变,是由外力的作用而产生的应变。第2项是压电应变,是在电场作用下产生的应变。
图 3为压电片电场方向示意图。
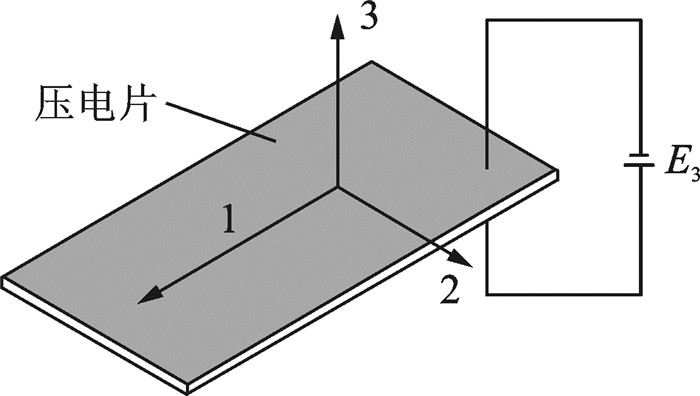
|
图 3 压电片电场方向 Figure 3 Electric field direction of piezoelectric sheet |
如图 3所示,一般情况下,压电材料是沿其厚度方向(即3方向)极化的,垂直极化方向的平面内表现为各向同性特性[13]。则其柔度系数矩阵可以表示为
| $ \mathit{\boldsymbol{s}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{S_{11}}}&{{S_{12}}}&{{S_{13}}}\\ {{S_{12}}}&{{S_{22}}}&{{S_{23}}}\\ {{S_{13}}}&{{S_{23}}}&{{S_{33}}} \end{array}}&{\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}}\\ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}}&{\begin{array}{*{20}{c}} {{S_{44}}}&0&0\\ 0&{{S_{55}}}&0\\ 0&0&{{S_{66}}} \end{array}} \end{array}} \right] $ | (2) |
式中:S12=S13,S11=S22,S44= S55。压电应变系数矩阵可以表示为
| $ \mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{d_{15}}}&0\\ 0&0&0&{{d_{15}}}&0&0\\ {{d_{31}}}&{{d_{31}}}&{{d_{33}}}&0&0&0 \end{array}} \right] $ | (3) |
常见的压电片采用的是压电材料的d31效应,沿3方向(即厚度方向)极化,并在3方向施加驱动电压,从而压电应变可以表示为
| $ {\mathit{\boldsymbol{\varepsilon }}^{\rm{E}}} = {\left[ {\begin{array}{*{20}{c}} {{d_{31}}}&{{d_{31}}}&{{d_{33}}}&0&0&0 \end{array}} \right]^{\rm{T}}}{E_3} $ | (4) |
则1方向(即长度方向)的压电应变可以表示为
| $ {\varepsilon _1} = {d_{31}}{E_3} = {d_{31}}\frac{V}{t} $ | (5) |
式中:V为施加的驱动电压,t为压电片的厚度。
1.2 Euler-Bernoulli压电悬臂梁结构本节中,应用Euler-Bernoulli梁模型给出了压电悬臂梁结构的位移表达式。假定:
(1) 压电悬臂梁变形时,压电梁的截面形状和几何参数保持不变。
(2) 不考虑压电梁横向剪切对弯曲变形的影响。
(3) 压电梁关于中性面对称。
(4) 基体、粘贴层和压电层作为连续结构,压电层和基体层的横截面上的应变呈线性分布。
图 4为Euler-Bernoulli梁微元和梁坐标示意图。
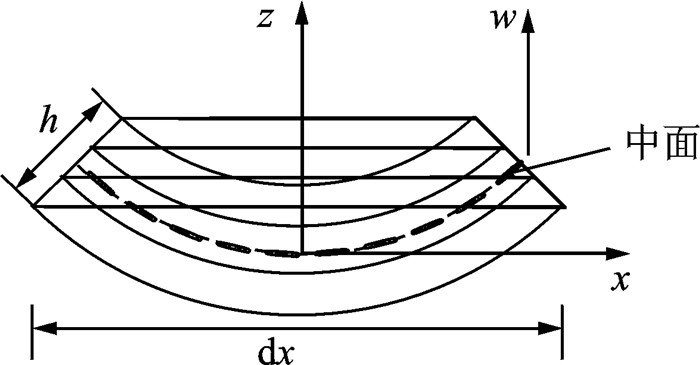
|
图 4 梁微元和梁坐标轴 Figure 4 Beam element and axis |
图 4中,轴向位移可以表示为
| $ u\left( {x,z} \right) = {u_0}\left( x \right) - z\frac{{\partial w\left( x \right)}}{{\partial x}} $ | (6) |
式中u0(x)为中性轴的轴向位移。因此,轴向应变随着厚度线性变化,可以表示为
| $ \varepsilon \left( {x,z} \right) = {\varepsilon _0}\left( x \right) - z\frac{{{\partial ^2}w\left( x \right)}}{{\partial {x^2}}} = {\varepsilon _0} - z\kappa $ | (7) |
式中弯曲曲率κ可以表示为
| $ \kappa = w'' = \frac{{{\partial ^2}w}}{{\partial {x^2}}} $ |
由压电本构关系可以导出压电层应力
| $ \sigma \left( {x,z} \right) = E\left( {x,z} \right)\left[ {{\varepsilon _0}\left( z \right) - \mathit{\Lambda }\left( {x,z} \right)} \right] $ | (8) |
将其简化得到
| $ \sigma \left( z \right) = E\left( z \right)\left[ {{\varepsilon _0}\left( z \right) - \mathit{\Lambda }\left( z \right)} \right] $ | (9) |
因为压电层是整梁的一部分,所以弹性模量E在z方向上是变化的。当Λ(z)=0时,基体层应力也可以由式(9)导出。设梁的总厚度为h(包括压电层)和宽度为b(z),轴向力可以表示为
| $ \begin{array}{*{20}{c}} {F = \int_{ - h/2}^{h/2} {b\left( z \right)\sigma \left( z \right){\rm{d}}z} = }\\ {\int_{ - h/2}^{h/2} {b\left( z \right)E\left( z \right)\left[ {{\varepsilon _0} - z\kappa - \mathit{\Lambda }\left( z \right)} \right]{\rm{d}}z} = }\\ {{\varepsilon _0}E{A_{{\rm{tot}}}} + \kappa E{S_{{\rm{tot}}}} - {F_\mathit{\Lambda }}} \end{array} $ | (10) |
| $ E{A_{{\rm{tot}}}} = \int_{ - h/2}^{h/2} {b\left( z \right)E\left( z \right){\rm{d}}z} $ | (11) |
| $ E{S_{{\rm{tot}}}} = \int_{ - h/2}^{h/2} {b\left( z \right)E\left( z \right)z{\rm{d}}z} $ | (12) |
| $ {F_\mathit{\Lambda }} = \int_{ - h/2}^{h/2} {b\left( z \right)E\left( z \right)\mathit{\Lambda }\left( z \right){\rm{d}}z} $ | (13) |
式中:FΛ表示由诱导应变引起的轴向力,EAtot表示总体拉伸刚度,EStot表示等效耦合刚度。
梁的总力矩可以表示为
| $ \begin{array}{*{20}{c}} {M = - \int_{ - h/2}^{h/2} {zb\left( z \right)\sigma \left( z \right){\rm{d}}z} = }\\ { - \int_{ - h/2}^{h/2} {zb\left( z \right)E\left( z \right)\left[ {{\varepsilon _0} - zk - \mathit{\Lambda }\left( z \right)} \right]{\rm{d}}z} = }\\ {{\varepsilon _0}E{S_{{\rm{tot}}}} + \kappa E{I_{{\rm{tot}}}} - {M_\mathit{\Lambda }}} \end{array} $ | (14) |
其中,
| $ E{I_{{\rm{tot}}}} = \int_{ - h/2}^{h/2} {b\left( z \right)E\left( z \right)z2{\rm{d}}z} $ | (15) |
| $ {M_\mathit{\Lambda }} = - \int_{ - h/2}^{h/2} {zb\left( z \right)E\left( z \right)\mathit{\Lambda }\left( z \right){\rm{d}}z} $ | (16) |
式中:MΛ表示由诱导应变引起的弯矩,EItot表示总体弯曲刚度。FΛ和MΛ是由压电层引起的,而基体层对其并无影响。将式(10,14)组合成矩阵方程
| $ \left\{ {\begin{array}{*{20}{c}} {F + {F_\mathit{\Lambda }}}\\ {M + {M_\mathit{\Lambda }}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {E{A_{{\rm{tot}}}}}&{E{S_{{\rm{tot}}}}}\\ {E{S_{{\rm{tot}}}}}&{E{I_{{\rm{tot}}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _0}}\\ {w''} \end{array}} \right\} $ | (17) |
如果结构不存在外力载荷,则F=0和M=0,矩阵方程变为
| $ \left\{ {\begin{array}{*{20}{c}} {{F_\mathit{\Lambda }}}\\ {{M_\mathit{\Lambda }}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {E{A_{{\rm{tot}}}}}&{E{S_{{\rm{tot}}}}}\\ {E{S_{{\rm{tot}}}}}&{E{I_{{\rm{tot}}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _0}}\\ {w''} \end{array}} \right\} $ | (18) |
假设整梁是由N层层合梁组成,每一层可以定义为主动层(压电层)或被动层(基体层或粘贴层),如图 5所示。
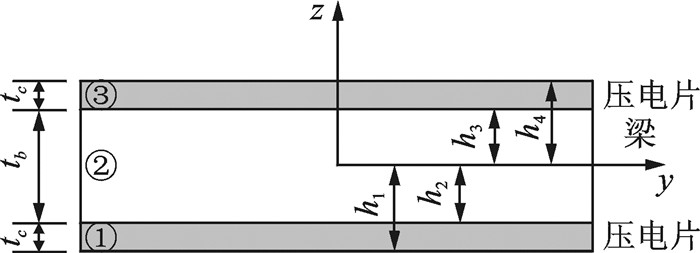
|
图 5 表面粘贴压电片的层合梁截面 Figure 5 Laminated beam section with piezoelectric sheet |
式(18)中的参数表达式为
| $ E{A_{{\rm{tot}}}} = \sum\limits_{k = 1}^N {{b_k}{E_k}\left( {{h_{k + 1}} - {h_k}} \right)} $ | (19) |
| $ E{S_{{\rm{tot}}}} = - \frac{1}{2}\sum\limits_{k = 1}^N {{b_k}{E_k}\left( {h{2_{k + 1}} - h{2_k}} \right)} $ | (20) |
| $ E{I_{{\rm{tot}}}} = \frac{1}{3}\sum\limits_{k = 1}^N {{b_k}{E_k}\left( {h{3_{k + 1}} - h{3_k}} \right)} $ | (21) |
| $ {F_\mathit{\Lambda }} = \sum\limits_{k = 1}^N {{\mathit{\Lambda }_k}{b_k}{E_k}\left( {{h_{k + 1}} - {h_k}} \right)} $ | (22) |
| $ {M_\mathit{\Lambda }} = - \frac{1}{2}\sum\limits_{k = 1}^N {{\mathit{\Lambda }_k}{b_k}{E_k}\left( {h{2_{k + 1}} - h{2_k}} \right)} $ | (23) |
式中:hk表示层合梁不同层之间界面相对于中性面的垂直位置,Λk表示层合梁每一层的自由应变,对于图 5的层合梁,其每一层的自由应变为
| $ {\mathit{\Lambda }_1} = \mathit{\Lambda },{\mathit{\Lambda }_2} = 0,{\mathit{\Lambda }_3} = - \mathit{\Lambda } $ | (24) |
式中
作为格尼襟翼的驱动机构,压电悬臂梁需要处于纯弯曲状态以达到最大挠度的要求。在纯弯曲状态下,FΛ=0,ε0=0。而且, 由于压电片是对称布置在基体上下面的,所以EStot=0。因此,式(18)变为
| $ {M_\mathit{\Lambda }} = E{I_{{\rm{tot}}}}w'' $ | (25) |
将参数代入式(21, 23)得到
| $ {M_\mathit{\Lambda }} = {E_c}{b_c}\mathit{\Lambda }{t_c}\left( {{t_b} + {t_c}} \right) $ | (26) |
| $ E{I_{{\rm{tot}}}} = E{I_b} + E{I_c} $ | (27) |
式中:EIb为基体层的弯曲刚度,EIc为压电层的弯曲刚度,其表达式为
| $ E{I_b} = \frac{{{E_b}{b_b}t{3_b}}}{{12}} $ | (28) |
| $ E{I_c} = \frac{{2{E_c}{b_c}t{3_c}}}{{12}} + 2{E_c}{b_c}{t_c}{\left( {\frac{{{t_c}}}{2} + \frac{{{t_b}}}{2}} \right)^2} $ | (29) |
位移表达式可由式(25)导出
| $ \frac{{{\partial ^2}w}}{{\partial {x^2}}} = \frac{{{M_\mathit{\Lambda }}}}{{E{I_{{\rm{tot}}}}}} $ | (30) |
| $ \left\{ \begin{array}{l} w = 0\;\;\;\;\;x < 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {31} \right)\\ w = \frac{{{M_\mathit{\Lambda }}}}{{E{I_{{\rm{tot}}}}}}\frac{{{x^2}}}{2}\;\;\;\;\;\;0 \le x \le {l_c}\;\;\;\;\;\;\;\;\;\;\;\left( {32} \right)\\ w = \frac{{{M_\mathit{\Lambda }}}}{{E{I_{{\rm{tot}}}}}}{l_c}\left( {x - \frac{{{l_c}}}{2}} \right)\;\;\;\;\;\;\;\;x > {l_c}\;\;\;\;\;\left( {33} \right) \end{array} \right. $ |
为了验证1.2节给出的位移表达式,本节利用有限元的方法对压电悬臂梁结构进行仿真,研究在不同参数条件下压电悬臂梁的输出位移变化。
图 6和表 1分别为压电悬臂梁的结构有限元模型和参数表。各结构层之间采用粘结的方式,由于电极层的厚度远远小于其他结构层的厚度,因此在有限元的压电分析中电极的厚度忽略不计。格尼尼襟翼驱动机构需要安装在桨叶内部,不仅要保证足够的输出位移,还必须结构紧凑、占用空间小。该压电悬臂梁是利用压电陶瓷材料的d31效应,为使悬臂梁自由端达到足够的位移,首先选用|d31|较大的PZT-5H材料,且产生相同的应变,PZT-5 H相对于其他压电材料需要较低的电压。
|
图 6 压电悬臂梁有限元模型 Figure 6 Finite element model of piezoelectric cantilever beam |
| 表 1 压电悬臂梁材料参数 Table 1 Material parameter of piezoelectric cantilever beam |
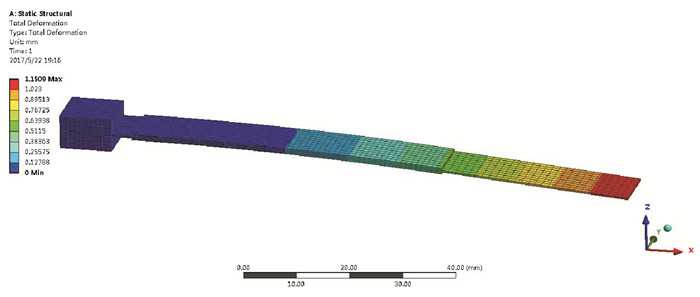
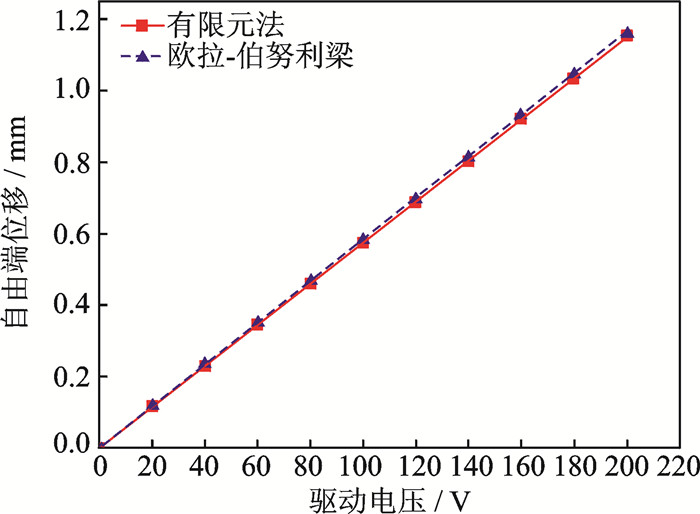
压电片的长宽厚分别为60,10,0.4 mm,基体的长宽厚分别为100,10,0.4 mm, 压电片以上下表面为电极可以视情况施加不同电压。施加电压后的悬臂梁模型如图 7所示。不同大小的驱动电压下的压电悬臂梁自由端位移情况如图 8所示,两种方法计算的结果表明,压电悬臂梁自由端位移与驱动电压成正比,并且表现出的线性非常好,在电压为200 V时悬臂梁自由端的位移可以达到1.15 mm。
|
图 7 施加电压后的悬臂梁模型 Figure 7 Beam model with driving voltage |
|
图 8 不同电压下的自由端位移 Figure 8 Displacement with driving different voltages |
3 结构参数对位移的影响
在限定的驱动电压条件下,压电悬臂梁的基体厚度、压电片的布置位置以及压电片的材料(即d31的大小)将直接影响悬臂梁的位移。本节通过第1和2节得出的位移表达式和有限元仿真的方法分析3个结构参数对悬臂梁自由端位移的影响。
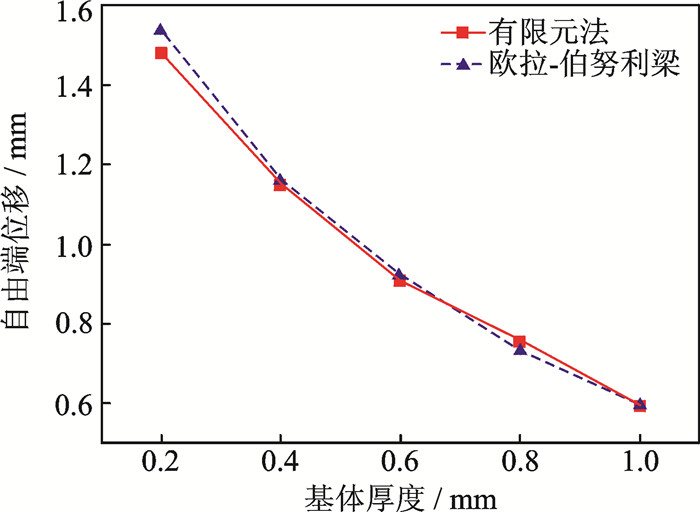
固定压电片与夹持装置的距离为4 mm,使基体层的厚度分别为0.2,0.4,0.6,0.8,1 mm,不同基体层差不超过2.6%。压电片距悬臂梁根部越远,位厚度对应的位移如图 9所示。两种方法的计算结果最大误差不超过3.6%。随着基体厚度的增加,自由端位移减小。这是由于随着基体厚度的增加,铝梁的弯曲刚度增加,压电层的相对刚度也随之增加,悬臂梁自由端的位移则随之减小。
|
图 9 基体厚度对自由端位移的影响 Figure 9 Influence of substrate thickness on displacement |
固定基体层的厚度为0.4 mm,使压电片与夹持装置的距离分别为4,12,20,28,36 mm,不同分布距离对应的自由端位移如图 10所示。两种方法的计算结果最大误差不超过2.6%。压电片距悬臂梁根部越远,位移越小。布置距离越远,相当于将基体的长度缩短,则自由端位移也越小。
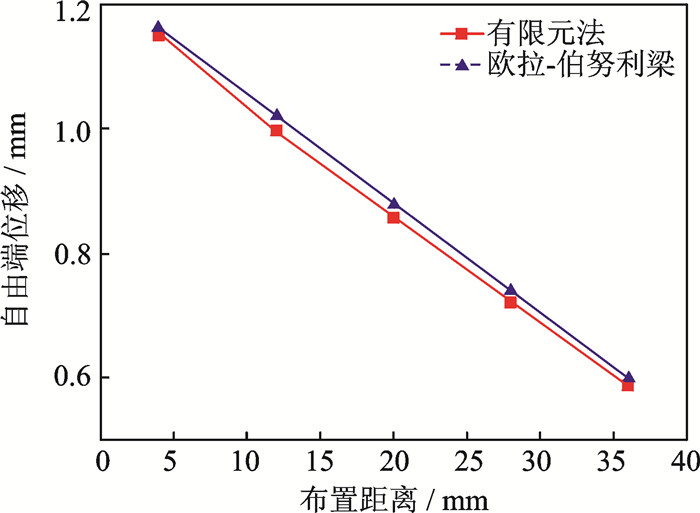
|
图 10 布置距离对自由端位移的影响 Figure 10 Influence of distance on displacement |
固定压电片与夹持装置的距离为4 mm以及基体层的厚度为0.4 mm,采用欧拉-伯努利梁方法计算的不同压电材料对应自由端位移如图 11所示。d31更大的的压电材料,自由端位移更大;而压电材料的弹性模量也会影响自由端位移,弹性模量越小,自由端位移越大,但是影响不明显。
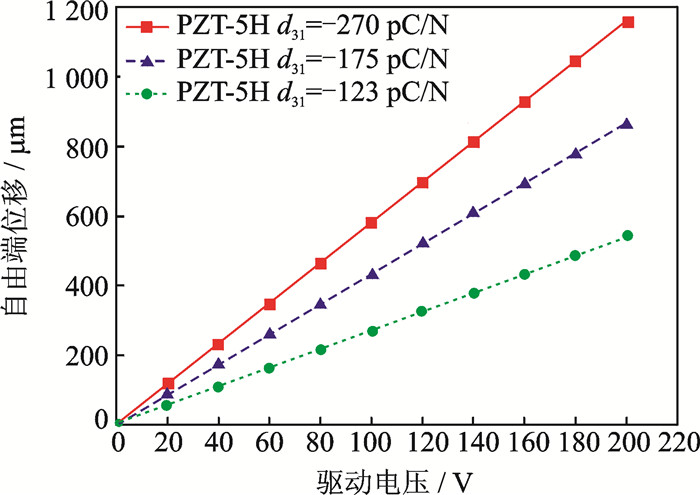
|
图 11 压电材料对自由端位移的影响 Figure 11 Influence of material on displacement |
4 结论
本文以压电悬臂梁作为格尼襟翼驱动机构进行研究,采用Euler-Bernoulli梁模型和有限元方法对压电悬臂梁端部位移进行了计算,得到了压电悬臂梁的位移表达式,并针对不同结构参数对位移的影响进行了仿真研究。研究结果表明:
(1) 压电悬臂梁基体的厚度对自由端位移的影响较大,在其他条件相同且抗弯刚度允许的情况下,选择较小厚度的基体有利于增加压电悬臂梁的位移。
(2) 压电片的位置靠近悬臂梁根部时,压电悬臂梁自由端的位移更大。
(3) 该压电悬臂梁利用的是压电材料的d31效应,压电参数中的d31值对自由端位移影响较大,d31越大,压电悬臂梁自由端位移越大。其中,弹性模量也会影响自由端位移,但是影响较小。
(4) 用压电悬臂梁驱动格尼襟翼的位移难以达到3%桨叶弦长,因此需要设计一种放大机构将压电悬臂梁的输出位移放大。该项工作还有待进一步研究。
| [1] |
KWANJUNG Y, WANDON J, LEE D H.
Aerodynamic performance analysis of a gurney flap for rotorcraft application[J]. Journal of Aircraft, 2007, 44(3): 1002–1014.
|
| [2] |
WEBB J, HIGGENBOTHAM H. Analysis of gurney flap effects on a NACA 0012 airfoil/wing section[C]//AIAA Applied Aerodynamics Conference. [S.l.]: AIAA, 2001. |
| [3] |
LI Yechen, WANG Jinjun, ZHANG Panfeng.
Effects of gurney flaps on a NACA0012 airfoil[J]. Flow, Turbulence and Combustion, 2002, 68(1): 27–39.
DOI:10.1023/A:1015679408150
|
| [4] |
LIBECK R H.
Design of subsonic airfoils for high lift[J]. Journal of Aircraft, 1978, 15(9): 547–561.
DOI:10.2514/3.58406
|
| [5] |
PALACIOS J, KINZEL M, OVERMEYER A.
Active gurney flaps:Their application in a rotor blade centrifugal field[J]. Journal of Aircraft, 2014, 51(2): 478–489.
|
| [6] |
THIEL M, LESIEUTRE G, MAUGHMER M, et al. Actuation of an active gurney flap for rotorcraft applications[C]//AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. [S.l.]: AIAA, 2013. |
| [7] |
HALL S, PRECHTL E.
Development of a piezoelectric servoflap for helicopter rotor control[J]. Active Materials and Smart Structures, 1995, 5(5): 16–29.
|
| [8] |
GUO Lei, QIN Yi. Modeling and analysis of a bimorph piezoelectric cantilever[C]//201613rd International Conference on Ubiquitous Robots and Ambient Intelligence. [S.l.]: IEEE, 2016: 248-251. |
| [9] |
李龙土, 邬军飞, 褚祥诚, 等.
压电双晶片的有限元分析及实验[J]. 光学精密工程, 2008, 16(12): 2378–2383.
DOI:10.3321/j.issn:1004-924X.2008.12.011 LI Longtu, WU Junfei, CHU Xiangcheng, et al. Finite element analysis and experiment on piezoelectric bimorph[J]. Optics and Precision Engineering, 2008, 16(12): 2378–2383. DOI:10.3321/j.issn:1004-924X.2008.12.011 |
| [10] |
程光明, 张海滨, 曾平, 等.
悬臂式压电双晶片振子夹持长度变化对其动态特性的影响[J]. 光学精密工程, 2014, 22(5): 1296–1303.
CHENG Guangming, ZHANG Haibin, ZENG Ping, et al. Effect of different clamping lengths of cantilever bimorph on its dynamic characteristics[J]. Optics and Precision Engineering, 2014, 22(5): 1296–1303. |
| [11] |
刘淑彦. 压电悬臂梁结构的动力学研究[D]. 北京: 北京工业大学, 2013.
LIU Shuyan. Dynamics study on the structure of piezoelectric cantilever[D]. Beijing: Beijing University of Technology, 2013.http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2448036 |
| [12] |
KEDZIORA P, MUC A.
Optimal shapes of PZT actutations for laminated structures subjected to displacement or eigenfrequency constraints[J]. Composite Structure, 2012, 94(3): 1224–1235.
DOI:10.1016/j.compstruct.2011.11.019
|
| [13] |
INMAN D J.
Smart structures theory[M]. Landon: Cambridge University Press, 2014.
|
 2018, Vol. 50
2018, Vol. 50


