动态失速现象在旋翼运动中尤为显著,旋翼桨叶在旋转过程中,来流速度、安装角等发生周期变化,加上旋翼尾迹畸变诱导的非均匀入流,会导致桨叶剖面在不同方位角处的迎角有很大差别。后行桨叶工作在大迎角状态,往往伴随着严重的动态失速问题。动态失速现象由前缘脱体涡主导,脱体涡快速后移,引起压力中心后移,从而产生很大的低头力矩,致使桨叶扭转载荷大幅增加。因此,进行准确的翼型动态失速分析对于提高直升机飞行性能、扩大飞行包线具有重要意义。
国外进行翼型动态失速数值计算的研究较早,文献[1, 2]对翼型的动态失速进行了早期研究,给出了充分的实验数据,由于当时计算流体动力学(Computational fluid dynamics, CFD)技术的限制,其数值计算结果无法体现部分流场特性;文献[3]在结构网格上对不可压流中翼型静、动态失速进行了数值计算,比较分析了大涡模拟(Large eddy simulation, LES)、RANS结合不同湍流模型对动态失速流场预测的有效性;文献[4]则建立了著名的L-B半经验模型,其能对翼型动态失速问题进行初步计算,在直升机设计中有着广泛应用。国内邵明玉等[5]对旋翼翼型进行了轻、深失速的初步探索,比较分析了计算力(矩)迟滞回线与实验数据的差异;近期赵国庆等[6]则采用嵌套网格方法,详细分析了平均迎角和缩减频率对动态失速的影响。
尽管CFD技术已经可以对旋翼翼型动态失速问题进行计算,但计算结果与实验数据常常存在较大差异。原因主要有两个:(1)翼型动态失速流场由涡运动主导,而数值格式往往伴随着一定的非物理耗散,网格离散也会带来网格耗散,这些都会导致流场失真;(2)物理模型,尤其是湍流模型和分离涡模型的有效性不足。
此外,上述研究中关于压缩性对动态失速的影响关注较少,仅有Leishman和McCroskey的研究中讨论了压缩性对力(矩)迟滞效应的影响。
针对以上问题,本文采用边界层流中效果良好的Roe格式以及应用广泛的k-ω SST湍流模型来进行动态失速流场的模拟;采用Weiss提出的预处理矩阵,来克服低速收敛困难问题;由于翼型不存在变形,采用自然满足几何守恒率(Geometric conservation law,GCL)的刚性动网格方法,以避免变形网格质量较差以及嵌套网格带来的插值降低精度等问题。最后,针对直升机旋翼翼型的典型运动流场工况,着重研究了马赫数对动态失速特性的影响。
1 离散方法 1.1 控制方程本文采用有限体积法进行偏微分方程的数值求解,任意拉格朗日欧拉法(Arbitrary Lagrangian-Eulerian method, ALE)形式的NS方程[7]
| $ \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{W}}{\rm{d}}\mathit{\Omega }} + \oint\limits_{\partial \mathit{\Omega }} {\left( {{\mathit{\boldsymbol{F}}_c} - {\mathit{\boldsymbol{F}}_v}} \right){\rm{d}}S} = \int_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}\mathit{\Omega }} $ | (1) |
式中:W为守恒变量, Fc为对流通量。
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho v}\\ {\rho w}\\ {\rho E} \end{array}} \right],{\mathit{\boldsymbol{F}}_c} = \left[ {\begin{array}{*{20}{c}} {\rho V}\\ {\rho \left( {u - {u_g}} \right)V + {n_x}P}\\ {\rho \left( {v - {v_g}} \right)V + {n_y}P}\\ {\rho \left( {w - {w_g}} \right)V + {n_z}P}\\ {\rho HV} \end{array}} \right] $ |
k-ω SST湍流模型由Menter[8]结合k-ω和高雷诺数k-ε模型得到,对核心湍流区和壁面附近都能进行较好的模拟,积分型控制方程为
| $ \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {{\mathit{\boldsymbol{W}}_T}{\rm{d}}\mathit{\Omega }} + \oint\limits_{\partial \mathit{\Omega }} {\left( {{\mathit{\boldsymbol{F}}_{c,T}} - {\mathit{\boldsymbol{F}}_{v,T}}} \right){\rm{d}}S} = \int_\mathit{\Omega } {{\mathit{\boldsymbol{Q}}_T}{\rm{d}}\mathit{\Omega }} $ | (2) |
式中:WT为守恒变量项;Fc, T, Fv, T为通量项。
NS方程和湍流模型方程中相关变量具体表达式在文献[8]中有详细描述, 湍流模型方程与主方程耦合求解。
1.2 低速预处理和时间离散本文采用Weiss等[9]提出的预处理方法,加入预处理矩阵后,控制方程为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}^{ - 1}}\frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{W}}{\rm{d}}\mathit{\Omega }} + \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{W}}{\rm{d}}\mathit{\Omega }} + \oint\limits_{\partial \mathit{\Omega }} {\left( {{\mathit{\boldsymbol{F}}_c} - {\mathit{\boldsymbol{F}}_v}} \right){\rm{d}}S} = }\\ {\int_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}\mathit{\Omega }} } \end{array} $ | (3) |
式中:Wp=[p u v w T]T,M为W对Wp的Jacobi矩阵,Γ为预处理矩阵。定义VAR矩阵为
| $ {\bf{VAR}} = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm var}} }&0&0&0&{{\rho _T}}\\ {{\mathop{\rm var}} \cdot u}&\rho &0&0&{{\rho _T} \cdot u}\\ {{\mathop{\rm var}} \cdot v}&0&\rho &0&{{\rho _T} \cdot v}\\ {{\mathop{\rm var}} \cdot w}&0&0&\rho &{{\rho _T} \cdot w}\\ {{\mathop{\rm var}} \cdot H - 1}&0&0&0&{{\rho _T}} \end{array}} \right] $ |
那么,M中
此时,特征矩阵的特征值为
| $ {\lambda _{1,2,3}} = \theta - {\mathit{\boldsymbol{V}}_g} \cdot \mathit{\boldsymbol{n}} $ |
| $ \begin{array}{*{20}{c}} {{\lambda _{4,5}} = \frac{{\beta - 1}}{2}\left( {\theta - {\mathit{\boldsymbol{V}}_g} \cdot \mathit{\boldsymbol{n}}} \right) \pm }\\ {\sqrt {{{\left( {\beta - 1} \right)}^2}{{\left( {\theta - {\mathit{\boldsymbol{V}}_g} \cdot \mathit{\boldsymbol{n}}} \right)}^2} + 4\beta {c^2}} } \end{array} $ |
注意到,当Ma∞→1, β→1,方程回归到没有预处理的情况。对低速流场,β值很小,系统矩阵的所有特征值大小保持在同一量级,使得预处理后的方程在所有速度范围内特征值都有良好的性态。
非定常计算对时间离散精度要求较高,采用二阶精度的三点后向差分进行离散
| $ \left[ {\left( {\frac{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\Omega }}}{{\Delta \tau }} + \frac{{3\mathit{\Omega }\mathit{\boldsymbol{I}}}}{{2\Delta t}}} \right) + \frac{{\partial \mathit{\boldsymbol{R}}}}{{\partial \mathit{\boldsymbol{W}}}}} \right]\Delta {\mathit{\boldsymbol{W}}^m} = - {\mathit{\boldsymbol{R}}^m}\left( {{\mathit{\boldsymbol{W}}^m}} \right) $ | (4) |
式中:Rm为新残差,见文献[7]。
根据文献[11],令
| $ \left[ {\frac{{\mathit{\Omega }\mathit{\boldsymbol{I}}}}{{\Delta \tau }} + \mathit{\boldsymbol{MS}}_p^{ - 1}\frac{{\partial \mathit{\boldsymbol{R}}}}{{\partial \mathit{\boldsymbol{W}}}}} \right]\Delta {\mathit{\boldsymbol{W}}^m} = - \mathit{\boldsymbol{MS}}_p^{ - 1}{\mathit{\boldsymbol{R}}^m}\left( {{\mathit{\boldsymbol{W}}^m}} \right) $ | (5) |
对于隐式的时间离散格式,具有直接法和迭代法两种求解方式,直接法计算量大。本文采用应用较广的LU-SGS[12]迭代法,LU-SGS分解法通过进行前后向两次迭代求解,避免了矩阵求逆。
LU-SGS方法进行前向和后向两次循环
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}}\Delta \mathit{\boldsymbol{W}}_i^1 = - \mathit{\boldsymbol{R}}_i^n - }\\ {\sum\limits_{j \in L\left( i \right)} {\frac{1}{2}\left[ {{{\left( {{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{S}}_p}\Delta \mathit{\boldsymbol{F}}_c^1} \right)}_j}\Delta {S_{ij}} - {{\left( {r_A^ * } \right)}_j}\mathit{\boldsymbol{\bar I}}\Delta \mathit{\boldsymbol{W}}_j^1} \right]} }\\ {\mathit{\boldsymbol{D}}\Delta \mathit{\boldsymbol{W}}_i^n = \mathit{\boldsymbol{D}}\Delta \mathit{\boldsymbol{W}}_i^1 - }\\ {\sum\limits_{j \in U\left( i \right)} {\frac{1}{2}\left[ {{{\left( {{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{S}}_p}\Delta \mathit{\boldsymbol{F}}_c^n} \right)}_j}\Delta {S_{ij}} - {{\left( {r_A^ * } \right)}_j}\mathit{\boldsymbol{\bar I}}\Delta \mathit{\boldsymbol{W}}_j^n} \right]} } \end{array} $ | (6) |
式中
| $ \mathit{\boldsymbol{D}} = \left( {\frac{\mathit{\Omega }}{{\Delta \tau }} + \frac{\omega }{2}{{\mathit{\bar \Lambda }}_c} + {{\mathit{\bar \Lambda }}_v}} \right)\mathit{\boldsymbol{I}} - \frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial \mathit{\boldsymbol{W}}}}\mathit{\Omega } $ |
| $ \mathit{r}_A^ * = \omega {{\bar \lambda }_c} + {{\bar \lambda }_v},\omega \in \left( {1,2} \right] $ |
| $ {{\mathit{\bar \Lambda }}_c} = \sum {{{\bar \lambda }_c}} = \sum {\rho \left( {\mathit{\boldsymbol{MS}}_p^{ - 1}\frac{{\partial {\mathit{\boldsymbol{F}}_c}}}{{\partial \mathit{\boldsymbol{W}}}}} \right)} $ |
| $ {{\mathit{\bar \Lambda }}_v} = \sum {{{\bar \lambda }_v}} = \sum {\rho \left( {\mathit{\boldsymbol{MS}}_p^{ - 1}\frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial \mathit{\boldsymbol{W}}}}} \right)} $ |
特征值具体表达式参考文献[11]。
需要注意的是,在运用LU-SGS迭代法前要对网格进行重排[13],提高收敛效率和稳定性。在运用湍流模型时,湍流方程源项中的消失项进行隐式处理,以增强对角矩阵的对角占优,提高迭代求解代数方程的稳定性,源项中其他部分则采用显示处理[14]。
1.3 空间离散由于双曲型方程有限的特征速度,对流项离散方法一直都是计算流体力学是研究的重点之一,其离散格式对结果的收敛性具有至关重要的影响。本文采用Roe[15]格式, Roe格式采用近似Riemann问题解来构造离散格式。其在边界层流中表现较好,针对激波具有高分辨率的特点。
添加预处理后,Roe格式也要进行相应变形,每条边上的通量离散格式为
| $ \begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{F}}_c}} \right)}_{ij}} = \frac{1}{2}\left[ {{\mathit{\boldsymbol{F}}_c}\left( {{\mathit{\boldsymbol{W}}_{\rm{R}}}} \right) + {\mathit{\boldsymbol{F}}_c}\left( {{\mathit{\boldsymbol{W}}_{\rm{L}}}} \right) - } \right.}\\ {\left. {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{M}}^{ - 1}}{{\left| {\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\mathit{\boldsymbol{\bar A}}} \right|}_{ij}}\left( {{\mathit{\boldsymbol{W}}_{\rm{R}}} - {\mathit{\boldsymbol{W}}_{\rm{L}}}} \right)} \right]} \end{array} $ | (7) |
式中:WR, WL网格界面左右状态值,详细表达式见文献[16]。
计算左右状态值的重构方法很多,如MUSCL重构、分段线性和分段二次重构等,本文采用广泛采用的具有二阶精度的线性重构[17]
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_{\rm{L}}} = {\mathit{\boldsymbol{U}}_i} + {\mathit{\Phi }_i}\left( {\nabla {\mathit{\boldsymbol{U}}_i} \cdot {\mathit{\boldsymbol{r}}_{\rm{L}}}} \right)}\\ {{\mathit{\boldsymbol{U}}_{\rm{R}}} = {\mathit{\boldsymbol{U}}_j} + {\mathit{\Phi }_j}\left( {\nabla {\mathit{\boldsymbol{U}}_j} \cdot {\mathit{\boldsymbol{r}}_{\rm{R}}}} \right)} \end{array} $ | (8) |
式中Φi为限制器,二阶精度以上迎风格式需要使用限制器,来降低边界上重构的梯度值,保证物理解的有界性。限制器有多种,本文采用文献[18, 19]中提出的限制器,此限制器具有出色的收敛特性,因此被广泛采用。
| $ {\mathit{\Phi }_i} = \left\{ \begin{array}{l} \frac{1}{{{\Delta _2}}}\left[ {\frac{{\left( {\Delta _{1,\max }^2 + {\varepsilon ^2}} \right){\Delta _2} + 2\Delta _2^2{\Delta _{1,\max }}}}{{\Delta _{1,\max }^2 + 2\Delta _2^2 + {\Delta _2}{\Delta _{1,\max }} + {\varepsilon ^2}}}} \right]\;\;\;\;\;{\Delta _2} > 0\\ \frac{1}{{{\Delta _2}}}\left[ {\frac{{\left( {\Delta _{1,\min }^2 + {\varepsilon ^2}} \right){\Delta _2} + 2\Delta _2^2{\Delta _{1,\min }}}}{{\Delta _{1,\min }^2 + 2\Delta _2^2 + {\Delta _2}{\Delta _{1,\min }} + {\varepsilon ^2}}}} \right]\;\;\;\;\;{\Delta _2} < 0\\ 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\Delta _2} = 0 \end{array} \right. $ | (9) |
式中:Φi为当前单元与相邻单元中的最小值,其余各项详见文献[18]。
1.4 边界条件物面边界速度满足无滑移条件:u=v=0并采用绝热壁和零压力梯度条件:
由于采用了预处理,流场的特征值发生了变化,基于Riemann不变量R1~4的无反射边界条件不能直接使用,本文采用简化远场边界条件[20]。
入流:
| $ {u_0} = {u_\infty },{v_0} = {v_\infty },{w_0} = {w_\infty },{T_0} = {T_\infty },{P_0} = {p_{{\rm{in}}}} $ |
出流:
| $ {u_0} = {u_{{\rm{in}}}},{v_0} = {v_{{\rm{in}}}},{w_0} = {w_{{\rm{in}}}},{T_0} = {T_{{\rm{in}}}},{P_0} = {p_\infty } $ |
下标0表示来流值,下标in表示内场值。
2 网格生成与几何守恒律结构网格正交性和贴体性较好,而对复杂边界适应性较差;非结构网格对复杂结构适应性好,但在物面处生成黏性网格质量差且数量大。本文结合结构网格和非结构网格的优点,在物面处,生成10~30层贴体网格,在外部则采用非结构网格。
2.1 结构网格生成结构网格生成一般进行要经过两步,第一步采用代数法进行法向外推,生成两层网格;之后采用椭圆形方程[21]对网格进行光顺,计算收敛后只保留第一层网格。一般在物面附近推进10~30层,椭圆形方程需要添加源项用于控制层间厚度,以获得能够辨析黏性子层的分辨率。
2.2 非结构网格生成在结构网格外层,采用阵面推进法[22]生成非结构网格。阵面推进法对不规则边界适应性较好,所以在贴体网格的外侧,即使出现长宽比很大的结构网格,其作为初始推进阵面也能顺利生成三角形网格。由于非结构网格分布在远离边界层的惯性较大的流场区域,使用较粗的非结构网格不会降低精度。
2.3 动网格和几何守恒律对于动态计算,有刚性网格和变形网格两种处理方法。刚性网格方法简单,但在远场边界可能会出现网格速度很大的情况,所以边界处需要特别处理。变形网格边界固定,但在物体运动过程中每次都要微调或者重新构造网格,降低计算效率。
由于本文计算的状态翼型不存在变形运动,所以采用随翼型运动的刚性网格方法[23],网格速度根据翼型运动方程计算。需要指出的是,如果采用的网格存在变形,必须考虑到几何守恒律[24],刚性运动网格自然满足几何守恒律。
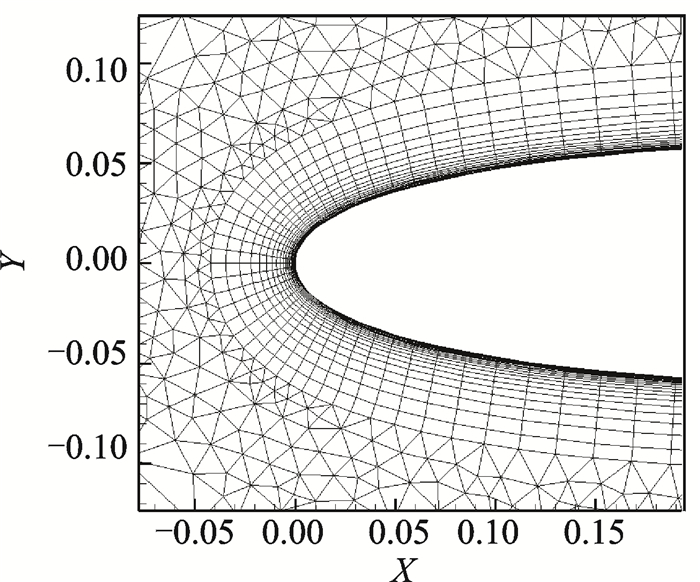
本文采用的网格结构(见图 1)网格部分为130×30,非结构网格单元总量为13 470。第一层网格厚度为1.0×10-6,以保证Y+≈1.0。
|
图 1 混合网格 Figure 1 Hybrid grid |
3 算例与结果分析 3.1 预处理和动网格方法验证
为验证本文所建立的计算方法在低速流动条件下的有效性,首先对比了预处理和不加预处理两种计算条件下,静态流场的收敛特性。选取NACA0012翼型,来流参数为:Ma∞=0.1, Re=1×106, α=5°。
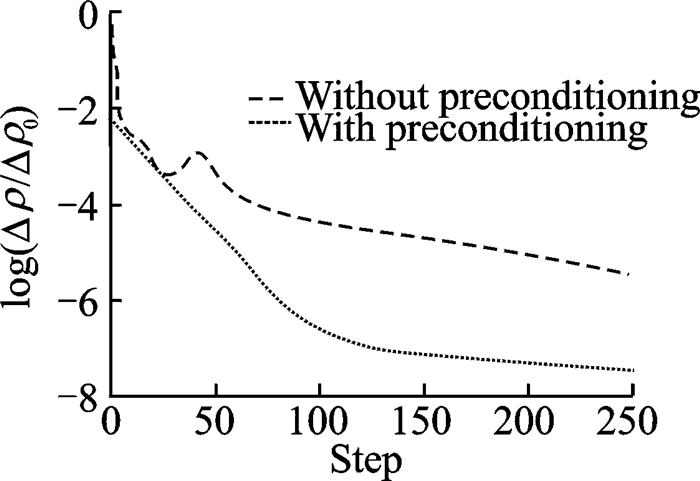
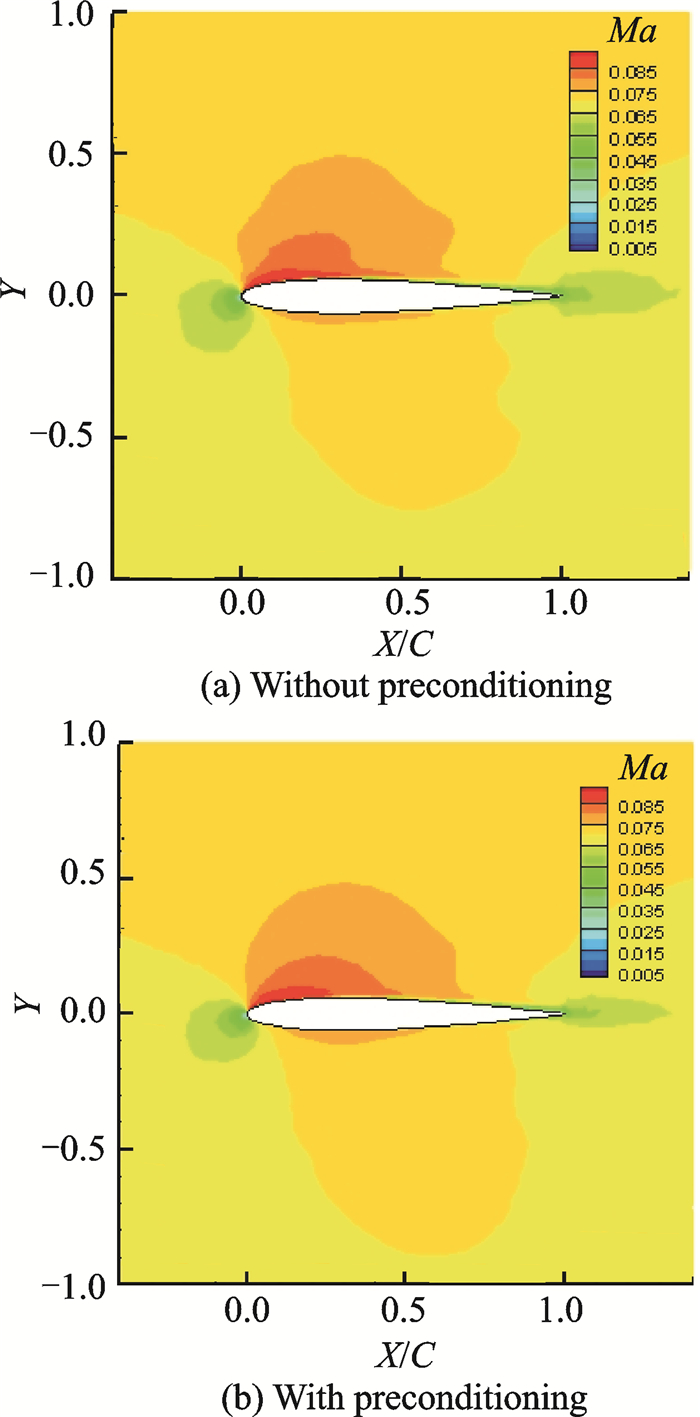
图 2为平均密度相对残差收敛曲线,图 3为流体等马赫数分布图。
|
图 2 平均密度收敛历程 Figure 2 Convergence history of mean density |
|
图 3 等马赫数分布图 Figure 3 Iso-Mach distribution |
从图中可以看出,添加预处理矩阵后,流场收敛速度和精度都有较大提高。结合流场马赫数云图,可以看出添加预处理后,流场振荡得到一定抑制,变量分布更为精确。
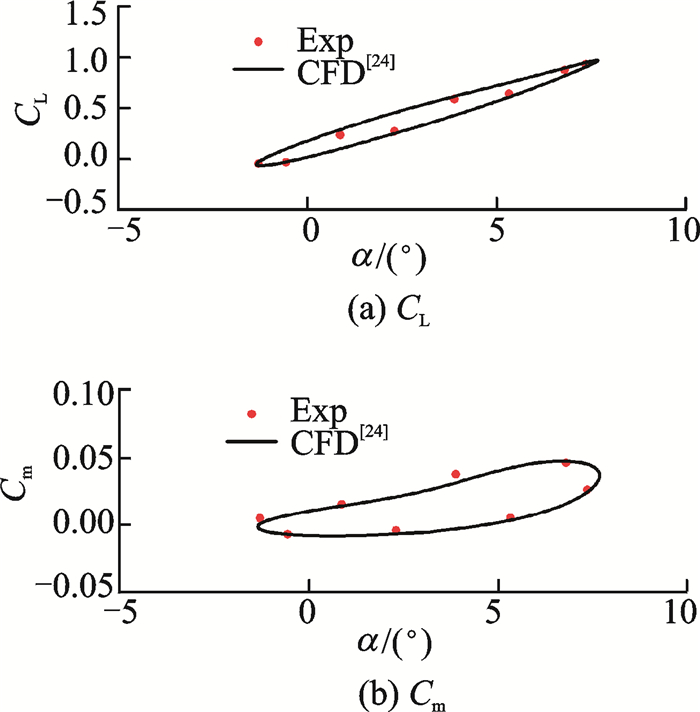
为验证本文所建立格式在翼型动态运动条件下的有效性,计算了翼型在正弦运动下的动态特性。NATO航天研究与发展咨询组公布的标准翼型在跨声速条件下作强迫俯仰振荡的实验结果[25]是CFD计算的标准考核算例。绕1/4弦线正弦振荡:α=3.16+4.59sinωt,
|
图 4 力(矩)系数迟滞回线 Figure 4 Lift and moment hysteresis |
由图 4中可以看出,计算结果与实验吻合较好,表明本文建立的计算方法对于亚声速动态流场具有较好的模拟能力。
3.2 轻失速计算分析轻失速出现在翼型振荡迎角超过静态失速迎角,但是超出程度不足以产生较大分离的情况下。为验证本文建立的计算方法的有效性,选取后行桨叶翼型典型工况进行轻失速计算,与实验[3]进行了对比。NACA0012翼型在Ma=0.3时,静态失速迎角在13.5°左右。
那么设置翼型运动条件为
| $ \alpha = 9.95 + 4.91\sin \omega t,kr = 0.099 $ |
来流参数为Ma∞=0.301, Re=3.88×106。
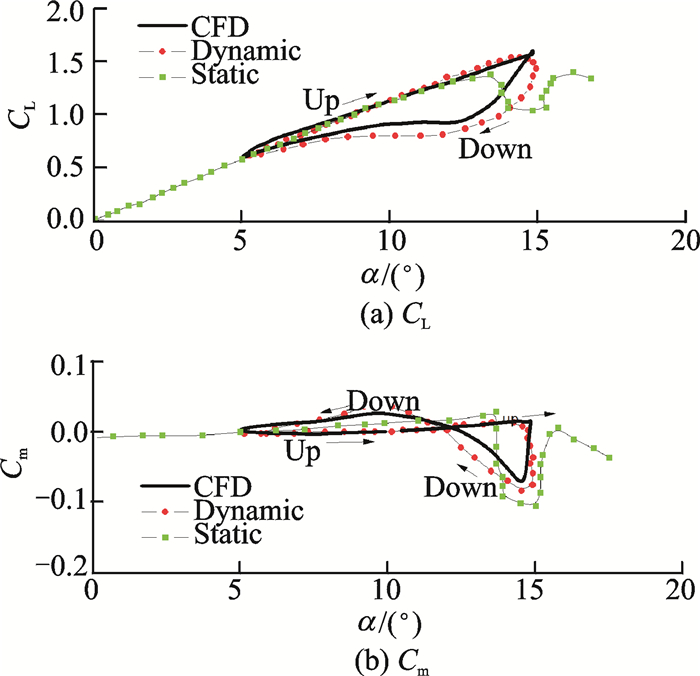
图 5为计算得到的力(矩)迟滞回线。
|
图 5 力(矩)迟滞回线 Figure 5 Lift and moment hysteresis |
从图 5中可以看出,动态失速相对静态失速出现了清晰的延迟,在达到最大迎角时,翼型尾缘开始出现较轻的回流,如图 6所示,之后尾缘会经历部分气流分离,导致轻失速的发生。在下行阶段,再附过程比实验相对较快,这是由于经验性的湍流模型带来的。总而言之,计算结果与实验数据吻合较好。
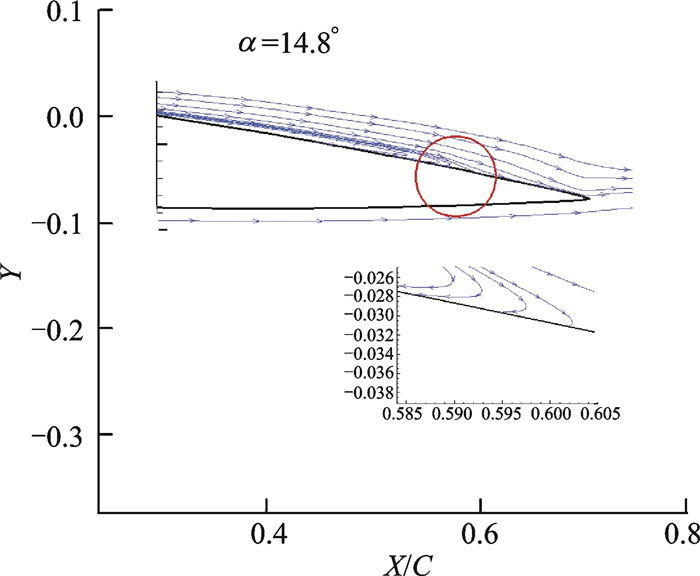
|
图 6 尾缘开始出现回流 Figure 6 Reverse flow near trailing edge |
3.3 深失速计算分析
为分析计算方法在翼型对深失速流场情况的计算能力,依旧选取后行桨叶典型动态失速剖面
特性作为仿真工况。那么设置翼型运动条件
| $ \alpha = 14.91 + 9.88\sin \omega t,kr = 0.151 $ |
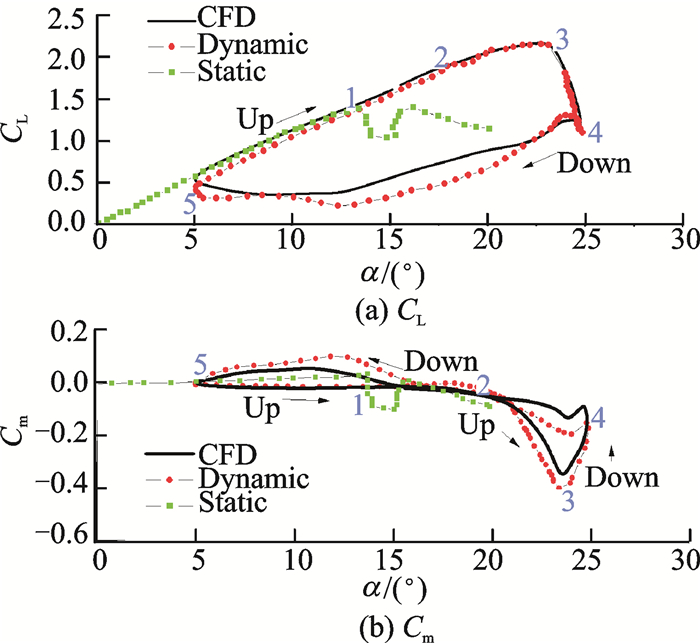
来流参数为Ma∞=0.288, Re=3.45×106, 计算结果如图 7所示。
|
图 7 深失速力(矩)迟滞回线 Figure 7 Lift and moment hysteresis |
由图 7可以清晰看到失速和再附的延迟性。力和(力矩)系数在下行阶段再附速度快于实验数据,而且力矩系数的峰值低于实验值。原因在于,深失速情况下,动态失速现象由前缘分离涡主导,由于现有湍流模型的局限性,很难精细模拟分离涡,所以给计算结果带来一定误差。
图 8中给出了图 7上不同标记点的流场情况,1~2阶段为刚过静态失速迎角阶段,尾缘开始出现回流;2点表示前缘脱体涡开始形成,其诱导出额外的升力,以及导致压力中心后移;2~3阶段脱体涡往尾缘运动,升力系数上升而力矩系数下降;3点表示脱体涡开始进入尾流,力矩系数达到最低,而上表面大部分进入气流分离,导致升力系数突降;5点表示气流开始再附,由于翼型运动的诱导弯度作用及分离流的影响,再附时刻也远低于静态失速迎角。
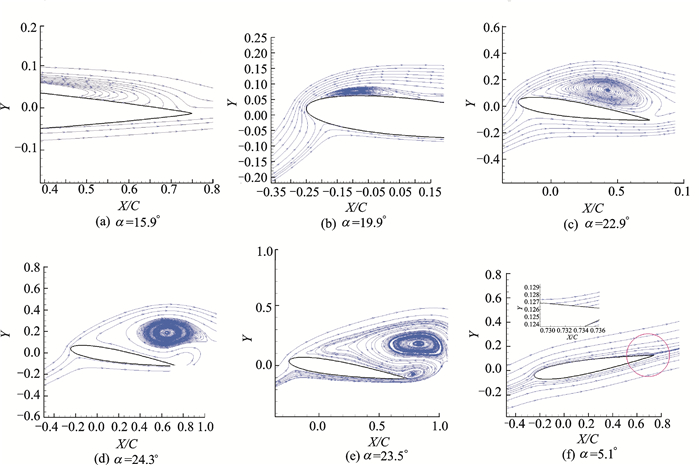
|
图 8 动态失速发展机理 Figure 8 Process of dynamic stall |
总体上看,本文所建立的计算方法精确捕捉到了深失速的发展过程,能够用来进行不同马赫数下动态失速分析。
3.4 马赫数对动态失速影响的计算分析影响动态失速的主要因素有平均迎角、缩减频率和来流马赫数,不同马赫数下(尤其是从不可压到可压)的研究较少,本文对这一情况进行了相关计算分析。
运动状态为
| $ \alpha = 15 + 10\sin \omega t,kr = 0.1 $ |
来流条件:Ma∞=0.18~0.36, Re=13·Ma∞×106。
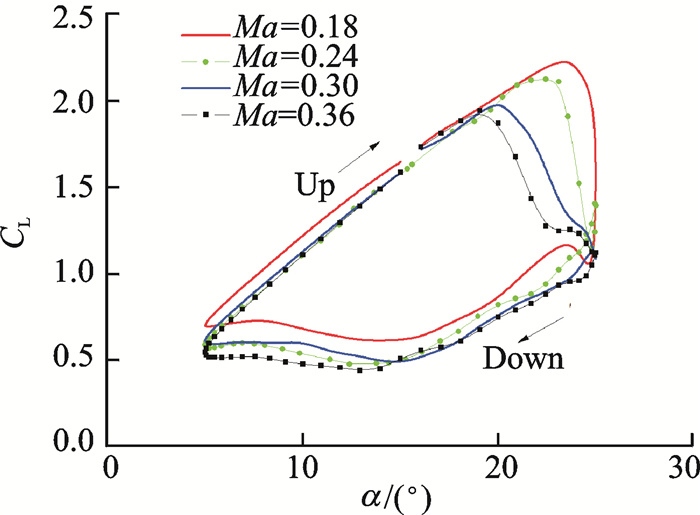
|
图 9 不同马赫数下升力系数迟滞回线 Figure 9 Hysteresis of lift coefficient at different Mach numbers |
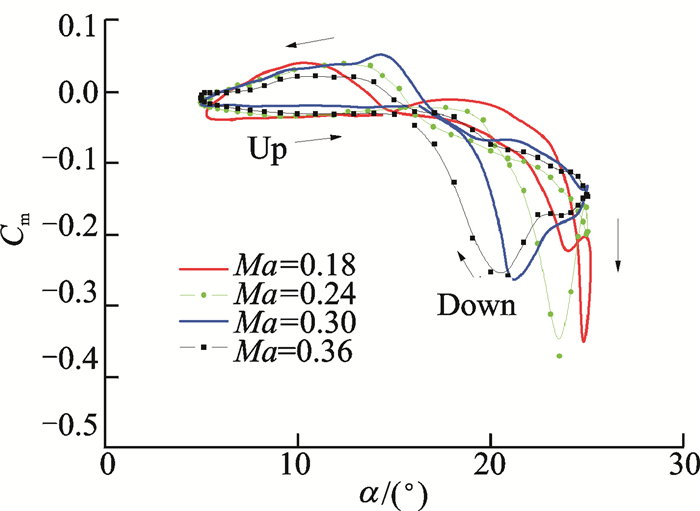
|
图 10 不同马赫数下力矩系数迟滞回线 Figure 10 Hysteresis of moment coefficient at different Mach numbers |
从图 9可以明显看出,随着来流马赫数的增大,翼型动态失速迎角越小,这与静态失速特性相符。随着马赫数增大,翼型最低压力点的压力有额外降低,导致翼型后部分的逆压梯度增大,从而更容易产生气流分离。此外,也可以看到,马赫数越大,气流再附速度也会有所降低。
观察力矩系数曲线,可以看出马赫数越小,最小力矩系数越小,这是由于压缩性使得翼型气流分离发生的更快,所以分离涡在翼型上表面没有得到充分的发展。
4 结论本文基于混合网格,采用RANS方程以及预处理技术构建了低速上旋翼翼型动态失速计算方法。通过以上研究分析,可以得到如下结论:
(1) 本文建立的计算方法能够精确模拟旋翼低速动态失速特性,可用于翼型大迎角下的动特性分析。
(2) 采用低速预处理技术和动网格技术,针对在低速流场和亚声速流场中的静、动态特性,都能给出较好的计算结果。预处理方法能够加速收敛和提高收敛精度,刚性动网格技术可用于翼型动态特性分析。
(3) 轻失速情况下,翼型只在尾缘部分发生分离,对升力系数失速延迟不大,附加的低头力矩也较弱;深失速出现明显的前缘分离涡,会导致升力系数失速迟滞,以及低头力矩的突降。
(4) 随着马赫数的增加,动态失速现象在更小的角度发生,再附速度减缓。且由于压缩性的影响,最大低头力矩增大。
| [1] |
MCCROSKEY W J, PHILIPPE J J.
Unsteady viscous flow on oscillating airfoils[J]. AIAA Journal, 1975, 13(13): 71–79.
|
| [2] |
MCALISTER K W, PUCCI S L, MCCROSKEY W J, et al. An experimental study of dynamic stall on advanced airfoil sections:Pressure and force data[R]. NASA TM-84245, 1982. |
| [3] |
KE Jianghua, EDWARDS J. RANS and LES/RANS simulation of airfoils under static and dynamic stall[C]//AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Texas:Published by the American Institute of Aeronautics and Astronautics, 2013. |
| [4] |
LEISHMAN J G.
Principles of helicopter aerodynamics[M]. New York: Cambridge University Press, 2006.
|
| [5] |
邵明玉, 杨茂, 陈凤明.
旋翼翼型动态失速特性的数值仿真研究[J]. 计算机仿真, 2012, 29(7): 70–74.
SHAO Mingyu, YANG Mao, CHEN Fengming. Numerical simulation study on dynamic stall characteristics of rotor airfoil[J]. Computer Simulation, 2012, 29(7): 70–74. |
| [6] |
赵国庆, 招启军, 王清.
旋翼翼型非定常动态失速特性的CFD模拟及参数分析[J]. 空气动力学学报, 2015, 33(1): 72–81.
ZHAO Guoqing, ZHAO Qijun, WANG Qing. Simulations and parametric analyses on unsteady dynamic stall characteristics of rotor airfoil based on CFD method[J]. Acta Aerodynamica Sinica, 2015, 33(1): 72–81. |
| [7] |
BLAZEK J.
Computational fluid dynamics:Principles and applications[J]. Computational Fluid Dynamics Principles & Applications, 2001, 14(1): 134–143.
|
| [8] |
MENTER F R.
Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598–1605.
DOI:10.2514/3.12149
|
| [9] |
WEISS J M, MARUSZEWSKI J P, SMITH W A.
Implicit solution of preconditioned Navier-Stokes equations using algebraic multigrid[J]. AIAA Journal, 1999, 37(1): 29–36.
DOI:10.2514/2.689
|
| [10] |
JESPERSEN D, PULLIAM T, BUNING P. Recent enhancements to overflow[C]//AIAA, Aerospace Sciences Meeting & Exhibit, 35th. Reno, NV:the American Institute of Aeronautics and Astronautics, 1997. |
| [11] |
PANDYA S A, VENKATESWARAN S, PULLIAM T H. Implementation of preconditioned dual-time procedures in overflow[C]//41st Aerospace Sciences Meeting & Exhibit. Reno, NV:American Institute of Aeronautics and Astronautics, 2003. |
| [12] |
JAMESON A, TURKEL E.
Implicit schemes and LU decompositions[J]. Mathematics of Computation, 1981, 156(37): 385–397.
|
| [13] |
SHAROV D, NAKAHASHI K, SHAROV D, et al. Reordering of 3-D hybrid unstructured grids for vectorized LU-SGS Navier-Stokes computations[C]//Computation Fluid Dynamics Conference.[S.l.]:AIAA, 2013. |
| [14] |
WILCOX D C. Turbulence modeling for CFD[M]. California:DCW Industries Inc., 2006:363-367. |
| [15] |
ROE P L.
Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1997, 135(81): 250–258.
|
| [16] |
WEISS J. Preconditioning applied to variable and constant density time-accurate flows on unstructured meshes[C]//25th AIAA Fluid Dynamics Conference. Colorado Springs, CO:American Institute of Aeronautics and Astronautics, 1994. |
| [17] |
BARTH T J, JESPERSEN D C. The design and application of upwind schemes on unstructured meshes[C]//27th Aerospace Sciences Meeting.Nevada: American Institute of Aeronautics and Astronautics, 1989. |
| [18] |
VENKATAKRISHNAN V. On the accuracy of limiters and convergence to steady state solutions[C]//31st Aerospace Sciences Meeting & Exhibit. Reno, NV: American Institute of Aeronautics and Astronautics, 1993. |
| [19] |
VENKATAKRISHNAN V.
Convergence to steady state solutions of the Euler equations on unstructured grids with limiters[J]. Journal of Computational Physics, 1995, 118(1): 120–130.
DOI:10.1006/jcph.1995.1084
|
| [20] |
TURKEL E. Preconditioning methods for low-speed flows[R]. ICASE Report No.96-57, 1996. |
| [21] |
THOMPSON J F, THAMES F C, MASTIN C W.
Automatic numerical generation of body-fitted curvilinear coordinate system for field containing any number of arbitrary two-dimensional bodies[J]. Journal of Computational Physics, 1974, 15(3): 299–319.
DOI:10.1016/0021-9991(74)90114-4
|
| [22] |
MCMORRIS H, KALLINDERIS Y.
Octree-advancing front method for generation of unstructured surface and volume meshes[J]. AIAA Journal, 1997, 35(6): 976–984.
DOI:10.2514/2.206
|
| [23] |
MARONGIU C M. A moving grid method for unsteady flow computations[C]//18th AIAA Computational Fluid Dynamics Conference. Miami, FL:American Institute of Aeronautics and Astronautics, 2007. |
| [24] |
THOMAS P D, LOMBARD C K.
Geometric conservation law and its application to flow computations on moving grids[J]. AIAA Journal, 1979, 17(10): 1030–1037.
DOI:10.2514/3.61273
|
| [25] |
LANDON R H. NACA 0012 oscillatory and transient pitching[R]. AGARD Report r-702, 1982. |
 2018, Vol. 50
2018, Vol. 50


