2. 中国直升机设计研究所, 景德镇, 333001
2. China Helicopter Research and Development Institute, Jingdezhen, 333001, China
复合推力高速直升机发展由来已久,但早期由于材料、电子、控制等方面的技术制约,直到最近几年才逐渐走向实用。以西科斯基X2直升机为代表的共轴刚性双旋翼复合推力高速直升机以前行桨叶概念(Advancing blade concept, ABC)旋翼为升力面和操纵面,尾部安置大推力螺旋桨[1]。安装ABC旋翼的X2复合推力高速直升机兼有直升机和固定翼飞机的优点,减少了对起降场地的要求,缩短了到达工作区域的时间,扩大了使用范围。此类复合推力高速直升机不仅可承担现有直升机所有的工作,而且还大大弥补了直升机在速度、航程等方面的不足,因此近年来成为了航空领域关注的热点。
直升机总体设计是直升机研制中最重要的环节之一,而总体参数设计是总体从概念设计到初步设计完成方案设计的主要内容之一[2]。直升机总体参数是总体方案的设计变量,与直升机的气动、操稳、动力学特性及部件重量甚至成本等有密切关系。因此,总体参数设计对方案有着决定性的影响[2]。目前而言,直升机总体参数的选择方法主要有3种:原准法、统计法及优化法[3]。而针对复合推力高速直升机总体参数设计的方法,国内外鲜有报道。另外,国内对常规直升机总体参数设计优化技术的研究主要以单目标优化设计为主[4]。
多目标优化设计在飞行器工程设计、生产技术、科研试验和项目管理等许多方面应用非常广泛。基于遗传算法的内在并行机制及其全局优化的特点,6σ设计考虑了研制过程中可能出现的一些不确定的影响因素,可提高优化结果可靠性和鲁棒性[5-6]。
与常规直升机不同,本文研究的是配有ABC旋翼和大推力螺旋桨装置的复合推力高速直升机,提出基于6σ设计和改进的遗传算法,对复合推力高速直升机总体参数进行了多目标优化研究,为研制军事或民用复合推力高速直升机提供参考。
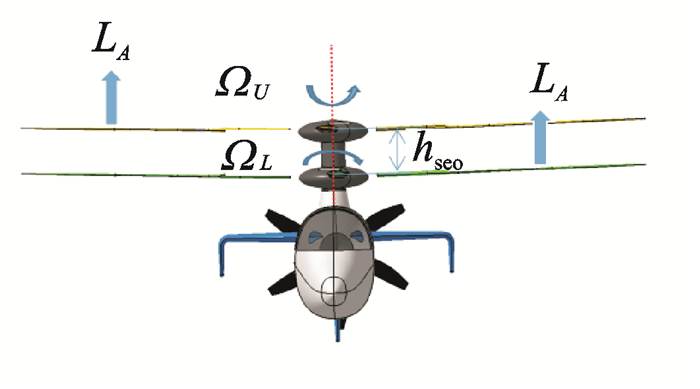
1 复合推力高速直升机总体参数 1.1 复合推力高速直升机及其参数特点ABC旋翼包括一对旋向相反,刚性的无铰式旋翼,在前飞速度较大时,桨盘两侧的前行桨叶将产生主要的气动升力,后行桨叶的升力载荷非常小,这样利用前行边的高升力对后行边的卸载作用,就可以减缓后行桨叶失速,因此解决了常规直升机受旋翼前行桨叶激波失速和后行桨叶气流分离而造成的速度问题。由于上下旋翼旋转方向相反,其桨叶前行区域分别位于机身左右两边,因此上下旋翼的反扭矩和倾转力矩可彼此相互平衡,其气动特点如图 1所示,因此不需要设置尾桨和挥舞铰。复合推力高速直升机的侧视简图如图 2所示。与常规直升机相比,随着前飞速度的增大,共轴刚性双旋翼复合推力高速直升机能够保持更高的升力和高速能力。
|
图 1 复合推力高速直升机旋翼桨叶升力分布示意图 Figure 1 Blade lift distribution diagram of high-speed compound helicopter |

|
图 2 复合推力高速直升机侧视简图 Figure 2 Simple side view of high-speed compound helicopter |
常规直升机桨尖速度一般为180~220 m/s[7],复合推力高速直升机要实现高速前飞,因此其桨尖速度要相对小一些;由于采用两副旋翼,与相同重量的单旋翼直升机相比,若桨盘载荷相同,其旋翼半径仅为单旋翼直升机的70%左右,且其旋翼实度较大。而共轴刚性双旋翼也会导致气动干扰载荷大、质量大、阻力大,振动大等问题,因此复合推力高速直升机的功率载荷较小,例如常规直升机UH-60的功率载荷为32 N/kW,而复合推力高速直升机X2的功率载荷仅为25.5 N/ kW。
1.2 总体参数分析复合推力高速直升机总体参数决定了其总体方案,包括:起飞重量G、旋翼半径R、旋翼桨尖速度ΩpR、功率载荷q、桨盘载荷p、旋翼实度σ、螺旋桨桨叶半径Rp、螺旋桨桨尖速度ΩpRp及双旋翼间距h等。
总体参数与气动、动力学、结构重量、噪声及操稳特性等有密切关系。设计选取这些参数很繁杂,甚至相互矛盾。给定设计任务或要求后,可以通过经验方法初步估算出总体参数。本文将把它们作为一组有效解带入到优化算法,和算法中其他随机产生的解作为初始值种群一起参与优胜劣汰的进化过程。
2 优化方法 2.1 多目标遗传算法优化一般来说,多目标优化其实是求解一组均衡解,即Pareto最优集,而不是单个的全局最优解。常规多目标优化问题求解方法是根据某效用函数将多目标合成单一目标来进行优化,但大多数情况下,在优化之前这种效用函数是难以确知的[5],且往往只能得到一个解,不能保证Pareto最优性。基于种群操作的遗传算法可以并行地搜索解空间的多个解,并利用不同解之间的相似性来提高其并发求解问题的效率,与Pareto最优概念相结合,产生基于Pareto最优概念的多目标优化的遗传算法。
遗传算法应用到多目标问题的最大困难是在没有给出决策偏好信息的前提下,难以直接衡量多目标问题的优劣,但通过对可行解之间的相互比较来淘汰劣解,可以达到对非劣解的逼近[8-11]。本文在改进的遗传算法的基础上基于Pareto概念,引入模糊理论,增加群体排序、小生境技术、精英保存策略进行多目标优化。通过模糊理论可处理好各目标函数和约束函数值量纲的不同,避免最优解丢失;将种群所有个体对各分目标表现进行排序,可得到表现矩阵,总体表现较优的个体能得到更大的适应度,获得更多参与进化的机会;通过侧重选择具有最小小生境数目的个体进行复制可以选择更优的候选解;取上一代进化产生的最好的n个解(一般取种群个体总数的5%~15%)作为现有非劣解集保存到下一代,对每一代进化的最优解与原有的非劣解进行比较,用产生的更好的解点进行置换。计算结束时得到的结果就是算法优化的非劣解。
2.2 6σ设计6σ由摩托罗拉公司于20世纪90年代中期提出,并逐渐从一种全面质量管理方法演变成为一个有效的企业流程设计、改造和优化技术。6σ设计源于数理统计知识,所谓σ是指统计学上的标准差,对于常规正态分布,随机变量在一次试验中,居于区间(均值-3σ,均值+3σ)的概率为99.73%,而居于(均值-6σ,均值+6σ)的概率为3.4×10-6[12]。实施6σ的优化设计,与实施6σ的企业及产品或服务一样,可以降低设计中的缺陷,提高设计水平[5]。
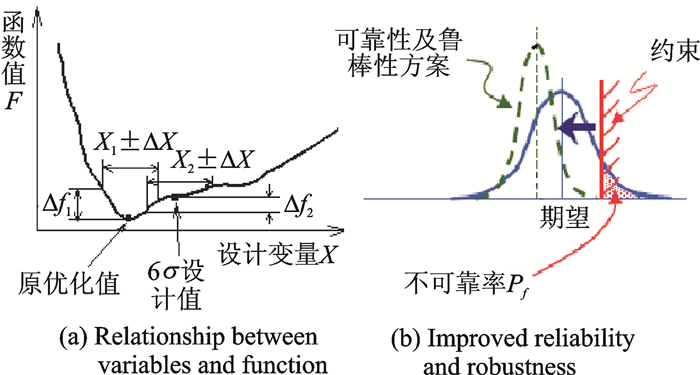
复合推力高速直升机总体设计过程中(主要是工程实践中)有许多不确定性因素,这些不确定性可能导致优化设计失败[2]。使用6σ设计,将屏蔽那些不确定性因素的影响。如图 3(a)所示,当设计变量有微小扰动ΔX的情况下,原优化函数值会有较大变化Δf1。经过6σ设计,当设计变量同样有微小扰动ΔX的情况下,优化函数值变化Δf2远小于Δf1。
|
图 3 6σ优化设计 Figure 3 Optimization design for 6σ |
在遗传算法进行最优化搜索确定性方案过程中,同时进行6σ设计,将会得到可靠性和鲁棒性非常好的优化结果,如图 3(b)所示。6σ优化设计的结果是处在变化相对比较缓和的解空间最低处(或最高处),不是全局的最低点(或最高点)。经过6σ优化设计后,即使设计变量发生漂移,引起约束和目标函数期望值的偏移,但最终优化结果有99.999 999 8%的概率落在期望值与6倍的标准差范围内。
6σ设计的步骤主要如下:
步骤1 基于改进的遗传算法,进行初步确定性优化设计。设计模型为:
| $ \begin{array}{l} {\rm{Max}}.\;\;\;\;F\left( \boldsymbol{X} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;{g_k}\left( \boldsymbol{X} \right) \le 0\\ \;\;\;\;\;\;\;\;\;{X_{\rm{L}}} \le \boldsymbol{X} \le {X_{\rm{U}}}\;\;\;\;\;\boldsymbol{X} = \left( {{x_1},{x_2}, \cdots ,{x_i}} \right) \end{array} $ |
由此得到一组解,即设计参数X。
步骤2 设计参数X中全部或某些参数发生变化,有小扰动偏移Xi,则相应函数有如下相应变化
| $ {\mu _y} = Y\left( {{\mu _x}} \right) + \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{{\partial ^2}Y}}{{\partial \boldsymbol{X}_i^2}}{{\left( {{\sigma _{{x_i}}}} \right)}^2}} $ | (1) |
| $ {\sigma _y} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {\frac{{\partial Y}}{{\partial {\boldsymbol{X}_i}}}} \right)}^2}{{\left( {{\sigma _{{x_i}}}} \right)}^2}} + \frac{1}{2}\sum\limits_i^n {\sum\limits_j^n {{{\left( {\frac{{{\partial ^2}Y}}{{\partial {\boldsymbol{X}_i}\partial {\boldsymbol{X}_j}}}} \right)}^2}{{\left( {{\sigma _{{x_i}}}} \right)}^2}{{\left( {{\sigma _{{x_j}}}} \right)}^2}} } } $ | (2) |
式中:Y为函数,μ和σ分别为所对应的参数或函数值的期望和标准差。
步骤3 设计模型修改为
| $ \begin{array}{l} {\rm{Max}}.\;\;\;\;F\left( {{\mu _f}\left( \boldsymbol{X} \right),{\sigma _f}\left( \boldsymbol{X} \right)} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;{g_k}\left( {{\mu _g}\left( \boldsymbol{X} \right),{\sigma _g}\left( \boldsymbol{X} \right)} \right) \le 0\\ \;\;\;\;\;\;\;\;\;{X_{\rm{L}}} \le {\mu _x} \pm 6{\sigma _x} \le {X_{\rm{U}}}\;\;\;\;\;\boldsymbol{X} = \left( {{x_1},{x_2}, \cdots ,{x_i}} \right) \end{array} $ |
步骤4 利用遗传算法世代更新不断搜索满足约束条件的最优值,直至满足优化终止条件。其中可靠率Pf要求达到6σ设计要求的99.999 999 8%,计算可靠率如下
| $ {P_f} = \mathit{\Phi }\left( t \right) = \frac{1}{{\sqrt {2{\rm{\pi }}} }}\int_{ - \infty }^t {{{\rm{e}}^{ - \frac{{{x^2}}}{2}}}{\rm{d}}x} $ | (3) |
应用本文研究的6σ设计方法和改进的遗传算法对复合推力高速直升机总体参数进行多目标优化设计,并以X2直升机为算例进行分析。
3.1 数学模型根据实际情况,总重G取X2直升机相同参数,以便对比分析。本文选择优化的总体参数为:旋翼桨叶半径R(因桨盘载荷p可由G和R计算得出,故不再列出),功率载荷q,旋翼实度σ,桨尖速度ΩR,双旋翼间距h,尾推螺旋桨半径Rp,尾推螺旋桨桨尖速度ΩpRp。本文拟设计变量X=[R, q, σ, ΩR, h, Rp, ΩpRp]T, X∈Rn。
根据统计规律及复合推力高速直升机设计经验和对已有复合推力高速直升机参数的归纳总结,给定各变量的取值范围如表 1所示。
| 表 1 设计变量的取值范围 Table 1 Value range of design variables |
表 1中,旋翼半径的变化范围是通过统计各类高速直升机的桨盘载荷换算所得。旋翼轴向间距则不能太小,因为间距太小会增加上下旋翼桨叶碰撞的危险,同时也不能太大,太大了机身结构不紧凑且会增加废阻功率。至于旋翼实度、尾推桨半径、尾推桨桨尖速度的变化范围则是直接定义在原值的±50%之内。
选择目标函数涉及到对复合推力高速直升机的使用要求和评价标准,本文以复合推力高速直升机的悬停效率和巡航换算生产率为目标函数。这两个目标综合考虑了复合推力高速直升机的气动力、飞行性能、经济性要求及动力装置的完善性,也分别考虑到了其垂直飞行和水平前飞性能。
本文以飞行性能为约束函数。飞行性能包括无地效悬停升限、最大平飞速度、最大爬升率、使用升限、航程和航时等。在优化模型中,约束条件表示如下
| $ \left\{ \begin{array}{l} {y_{k1}} \le {g_k}\left( \boldsymbol{X} \right) \le {y_{k2}}\;\;\;k = 1,2, \cdots ,n\\ a \le {x_t} \le b\;\;\;{x_t} \in \boldsymbol{X},\;\;t = 1,2, \cdots ,7 \end{array} \right. $ | (4) |
式中:gk(X)为约束函数;a,b,yk1和yk2为取值范围。考虑到多目标优化中各约束函数值的量纲不同,数值相差也很大,如果直接把它们带入适应度函数,函数值小的其重要程度就会降低,会导致最优解丢失。因此,这里将建立模糊物元模型以改善这一状况。因为带有约束条件,故新构造的目标函数由罚函数法将有约束非线性规划问题转化为无约束非线性规划问题
| $ \begin{array}{*{20}{c}} {{G_k}\left( \boldsymbol{X} \right) = \min \left[ {\left( {{g_k}\left( \boldsymbol{X} \right) - {y_{k1}}} \right)/{y_{k1}},} \right.}\\ {\left. {\left( {{y_{k2}} - {g_k}\left( \boldsymbol{X} \right)} \right)/{y_{k2}},0} \right]} \end{array} $ | (5) |
各分目标构造成新的目标函数
| $ \begin{array}{*{20}{c}} {{\rm{Max}}{\rm{.}}\;\;{R_t}\left( \boldsymbol{X} \right) = {F_t}\left( \boldsymbol{X} \right) + {M_1}\sum\limits_{k = 1}^n {\left[ {{G_k}\left( \boldsymbol{X} \right)} \right]} + {M_2}}\\ {t = 1,2} \end{array} $ | (6) |
式中:M1为罚函数的罚因子,M2为为保证目标函数值为正数而给定的一个较大常数。根据6σ设计要求修改数学模型,其中式(4)约束条件修改为
| $ \left\{ \begin{array}{l} {y_{k1}} + 6{\sigma _{gk}} \le {\mu _{gk}}\left( \boldsymbol{X} \right) \le {y_{k2}} + 6{\sigma _{gk}}\;\;\;\;k = 1,2, \cdots ,n\\ a + 6{\sigma _{xt}} \le {\mu _{xt}} \le b - 6{\sigma _{xt}}\;\;\;\;{x_t} \in X,t = 1,2, \cdots ,7 \end{array} \right. $ | (7) |
式(6)分目标函数修改为
| $ {\rm{Max}}.\;\;{\mu _{Rx}}\left( \boldsymbol{X} \right) - {\sigma _{Rx}}\left( \boldsymbol{X} \right) $ | (8) |
式中:μ和σ分别为所对应的参数或函数值的期望和标准差,其下标表示所对应的函数。
计算复合推力高速直升机性能重点是解决以旋翼和螺旋桨气动分析为基础的功率计算。复合推力高速直升机功率计算包括需用功率(机身废阻功率、旋翼诱导功率和型阻功率)和可用功率(螺旋桨有效功率)计算。本文用叶素理论和数值积分的方法计算需用和可用功率
| $ {P_{可用}} = \frac{1}{2}\rho V_0^3{k_p}\int_{{r_p}}^{{R_p}} {\frac{{{C_{\rm{L}}}b{{\left( {1 + a} \right)}^2}}}{{{{\sin }^2}\varphi \cdot \cos \gamma }} \cdot \cos \left( {\varphi + \gamma } \right){\rm{d}}r} $ | (9) |
| $ \begin{array}{*{20}{c}} {{P_{需用}} = \frac{1}{2}\rho V_0^3S{c_x} + }\\ {\frac{{k{V_0}}}{{\rm{\pi }}}\int_{\mathit{\Psi } = 0}^{2\pi } {\int_0^{{R_0}} {\left( {{\rm{d}}F_X^A + {\rm{d}}F_X^I + {\rm{d}}F_X^G} \right){\rm{d}}r{\rm{d}}\mathit{\Psi }} } } \end{array} $ | (10) |
式中:ρ为空气密度,γ为叶素阻升角,φ为桨叶合速度与旋转平面的夹角,a为干涉系数,bp为螺旋桨弦长,kp为桨叶片数,CL为叶素升力系数,rp为桨毂半径,V0为前飞速度,S为机身参考面积,cx为机身阻力系数,dFA为叶素气动力,dFI为叶素惯性力,dFG为叶素重力,下标X表示纵向。
3.2 优化设计以基于6σ设计的改进遗传算法多目标优化复合推力高速直升机总体参数。本文设定个体编码串长度为48,遗传算法控制参数群体规模N为120、自适应交叉概率Pc范围为0.4~0.9、自适应变异概率Pm范围为0.001~0.1和更新进化代数G为80。
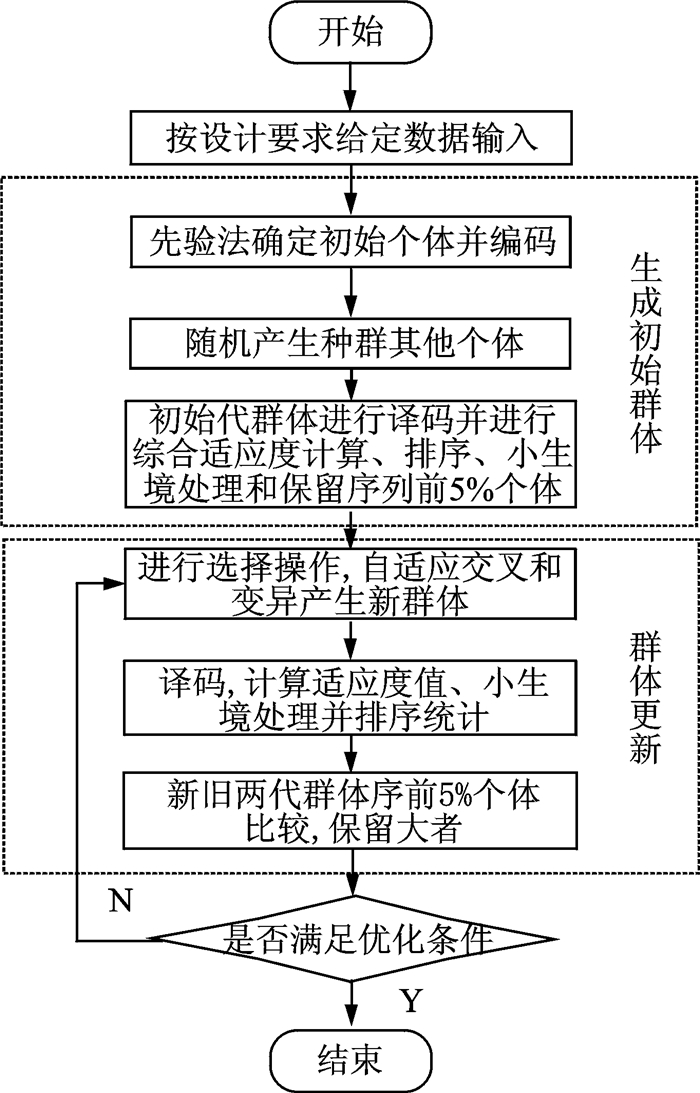
本文多目标优化设计具体步骤如图 4所示。
|
图 4 多目标优化流程框图 Figure 4 Flow block diagram of multiobjective optimization |
优化运算结束将产生Pareto最优解,对设计者或决策者来说这些解都是满意的,可任选其一。或根据设计经验或偏好选择其一,也可以通过定义满意度函数(满意度函数越大则解越优)来进行选择。本文满意度函数定义如下
| $ E = \frac{{{R_1} - {R_{1\min }}}}{{{R_{1\max }} - {R_{1\min }}}} + \frac{{{R_2} - {R_{2\min }}}}{{{R_{2\max }} - {R_{2\min }}}} $ | (11) |
式中:R1min和R1max分别为Pareto最优解集中子目标函数R1的最小值和最大值;R2min和R2max分别为最优解集中子目标函数R2的最小值和最大值。
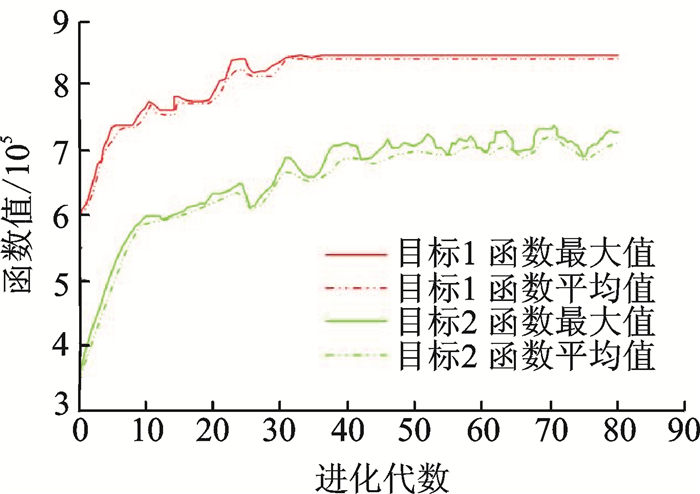
4 优化结果分析及结论基于6σ设计的多目标遗传算法优化经过80代运算,运算中种群个体对各分目标函数值变化过程如图 5所示,在更新换代至27代左右最大值个体出现。表 2则给出了多目标优化设计结果和原准机数据。另外,对总体参数优化前后的飞行性能进行了计算,如表 3所示。
|
图 5 进化历程 Figure 5 Evolutionary process |
| 表 2 总体参数多目标优化设计结果 Table 2 Results of multiobjective optimization design for general parameters |
| 表 3 总体参数优化前后的飞行性能对比 Table 3 Comparison of flight performance before and after optimization of general parameters |
表 2, 3中的优化结果满足X2复合推力高速直升机性能要求,各性能和参数可靠率Pf都达到99.999 999 8%,而原准机(X2复合推力高速直升机)设计参数最低Pf只有59.3%。从表中数据可以看出,经遗传算法和6σ设计优化后的各设计参数对应的复合推力高速直升机飞行性能除最大前飞速度刚满足设计约束(≥480 km/h)外,其他都有了一定的提高(注:X2性能数据不全,本文采用的是X2原机参数上的计算值,以此为原机值进行优化对比),目标值都较原准机大,且可靠性更高。最大前飞速度有所下降的原因如下:在总重不变的条件下,优化后的旋翼半径相对原值有所提高有利于降低桨盘载荷从而提高功率载荷,即有效功率相对下降了,故最大前飞速度略有下降。另外旋翼半径的增加会引起全机废阻增加,这使得直升机在高速性能方面略有下降,最大前飞速度也会因此略有下降。在分析研究了复合推力高速直升机气动特性和总体参数设计特点的基础上,本文结合改进的遗传算法和6σ设计技术,很好地解决了复合推力高速直升机总体参数多目标优化设计这类复杂非线性问题。遗传算法搜索到了很多潜在的、重要的、可能不会被设计师所能考虑到的参数组,而6σ设计提高了优化设计结果的可靠性和鲁棒性。改进的遗传算法结合6σ设计使优化结果更可靠、更完善、更具有实用价值。从优化设计结果可以看出优化效果良好,说明本文的优化设计方法是可行的,本设计方法及其程序已用于复合推力高速直升机的总体设计,将也可推广用于其他多目标参数决策领域。
| [1] |
RUDDELL A J.
Advancing blade concept (ABC) development[J]. Journal of the American Helicopter Society, 1976, 22(1): 13–23.
|
| [2] |
张呈林, 郭才根.
直升机总体设计[M]. 北京: 国防工业出版社, 2006.
ZHANG Chenglin, GUO Caigen. Helicopter general design[M]. Beijing: National Defence Industry Press, 2006. |
| [3] |
倪先平, 朱清华.
直升机总体设计思路和方法发展分析[J]. 航空学报, 2016, 37(1): 17–29.
NI Xianping, ZHU Qinghua. Development of ideas and methods of helicopter general design[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 17–29. |
| [4] |
丁亮. 重型直升机总体参数优化设计[D]. 南京: 南京航空航天大学, 2008.
DING Liang. Optimum design of heavy-lift helicopter general parameters[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2008. |
| [5] |
TAYLOR Z, RANGANATHAN S.
Designing high availability systems[M]. Piscataway: IEEE Press, 2014.
|
| [6] |
SANG W L, KWON O J.
Robust airfoil shape optimization using design for six sigma[J]. Journal of Aircraft, 2006, 43(3): 843–846.
DOI:10.2514/1.17359
|
| [7] |
WALSH D, WEINER S, ARIFIAN K, et al. Development testing of the Sikorsky X2 technology demonstrator[C]//American Helicopter Society 65th Annual Forum. Grapevine, Texas:[s.n.], 2009. |
| [8] |
崔逊学.
多目标进化算法及其应用[M]. 北京: 国防工业出版社, 2006: 242-247.
CUI Xunxue. Multiobjective evolutionary algorithms and their applications[M]. Beijing: National Defence Industry Press, 2006: 242-247. |
| [9] |
冯秋红, 刘全坤, 胡龙飞.
基于多目标优化的扁挤压筒结构设计[J]. 中国机械工程, 2006, 17(17): 1850–1853.
DOI:10.3321/j.issn:1004-132X.2006.17.021 FENG Qiuhong, LIU Quankun, HU Longfei. Structural design of flat extrusion container based on multi-objective optimization[J]. Journal of Chinese Mechanical Engineering, 2006, 17(17): 1850–1853. DOI:10.3321/j.issn:1004-132X.2006.17.021 |
| [10] |
李登峰.
模糊多目标多人决策与对策[M]. 北京: 国防工业出版社, 2003: 58-113.
LI Dengfeng. Fuzzy multiobjective many-person decision makings and games[M]. Beijing: National Defence Industry Press, 2003: 58-113. |
| [11] |
金东海, 桂幸民.
应用多目标遗传算法的叶栅气动优化设计[J]. 航空动力学报, 2006, 22(2): 285–290.
JIN Donghai, GUI Xingmin. Aerodynamic design optimization of cascade airfoils based on multi-objective genetic algorithm[J]. Journal of Aerospace Power, 2006, 22(2): 285–290. |
| [12] |
陈秋圣. 六西格玛设计在内饰声学件开发中的研究与应用[D]. 上海: 上海交通大学, 2013.
CHEN Qiusheng. Design for six sigma application on interior acoustic parts development[D]. Shanghai:Shanghai Jiao Tong University, 2013. |
 2018, Vol. 50
2018, Vol. 50


