2. 南京航空航天大学旋翼动力学国家级重点实验室, 南京, 210016
2. State Key Laboratory of Helicopter Rotorcraft Aeromechanics, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
随着直升机在现代战场中的广泛应用,对直升机,尤其是执行战场侦察和监控任务的无人直升机续航能力的要求越来越高。目前,提高无人直升机续航性能的一个重要措施就是根据直升机的飞行速度、飞行高度和飞行质量变化,调整旋翼转速,使得直升机旋翼尽量工作在最优转速附近,可以达到降低需用功率和耗油率从而提高续航性能的目的[1-2]。波音公司开发的A-160“蜂鸟”无人直升机,由于使用了变转速旋翼,能够在不同状态下控制最佳转速,其性能提升非常明显。
近几年国内外学者对变转速旋翼技术已经做了一些研究。1999年Karem申请了Optimum Speed Rotor专利,介绍了变转速旋翼的工作原理[3]。Steiner通过建模分析研究了变转速旋翼对美国UH-60A“黑鹰”直升机配平与性能的影响[4]。Guo进行的研究主要集中于直升机变转速旋翼的稳定性、操纵性与飞行控制[5]。Diottavio分析了A-160无人直升机的飞行性能,总结了变转速技术对旋翼升阻比、需用功率的影响[6]。马里兰大学的Chopra教授开展了变转速旋翼关于性能和振动载荷的风洞试验研究[7-8]。Anubhav等利用全尺寸UH-60A旋翼在风洞中,进行了降低旋翼转速, 前进比达到1.0的试验[9]。韩东教授针对旋翼变转速,研究了直升机的飞行性能及配平,并开展了旋翼试验[10-12]。
目前,国内外对变转速旋翼的研究,主要集中在气动配平、需用功率等飞行性能方面[13],但对不同飞行状态下旋翼转速优化路径、飞行过程中质量动态变化对续航性能的影响,以及旋翼转速的档位设计等研究较少。需要针对变转速直升机的工程设计,利用直升机常规性能分析模型,开展最低需用功率约束下飞行质量、高度和速度的变化对最优旋翼转速的影响规律分析,并根据规定载油量下可以达到的最久航时,探讨可行的旋翼转速变化档位选择。
本文以AC311直升机为例进行直升机续航性能(航程和航时)分析,评估变转速旋翼对续航性能的影响。并以降低需用功率为目标,进行旋翼转速优化设计。由于转速连续变化的工程实现难度大,提出了有级变速策略。
1 续航性能计算模型 1.1 需用功率计算模型在满足旋翼平衡和全机配平方程的条件下计算旋翼需用功率,分析优化转速旋翼性能和转速优化路径的影响因素。
本模型中直升机需用功率由旋翼的诱导功率Pi、型阻功率Pc、废阻功率Pp、尾桨需用功率Ppt,以及发电机、冷却系统、传动系统损耗等其他功率Pelse组成,需用功率系数表达式如下
| $ \begin{array}{l} {C_{\rm{p}}} = {C_{{\rm{po}}}} + {C_{{\rm{pp}}}} + {C_{{\rm{pi}}}} + {C_{{\rm{pt}}}} + {C_{{\rm{pelse}}}}\\ \left\{ \begin{array}{l} {C_{{\rm{po}}}} = \int {\int {\frac{{\sigma {C_{\rm{d}}}}}{2}} } {u^3}{\rm{d}}r{\rm{d}}\psi \\ {C_{{\rm{pp}}}} = \frac{1}{2}{\mu ^3}\frac{{{C_{fx}}{A_f}}}{A}\\ {C_{{\rm{pi}}}} = \int {\int {{\lambda _i}\sigma a{F_Z}{\rm{d}}r{\rm{d}}\psi } } \\ {C_{{\rm{pt}}}} = {C_{{\rm{pot}}}} + {C_{{\rm{pit}}}}\\ {C_{{\rm{pelse}}}} \approx 0.05({C_{{\rm{po}}}} + {C_{{\rm{pp}}}} + {C_{{\rm{pi}}}} + {C_{{\rm{pt}}}}) \end{array} \right.{\rm{ }} \end{array} $ |
式中:σ为旋翼实度,μ为前进比,λ为流入比,a为翼型升力线斜率,Fz为桨叶剖面拉力系数,u为剖面无因次合速度,Cfx为机身/桨毂阻力系数,Af为机身参考面积,A为桨盘面积。
1.2 航程计算模型与流程最大航程一般取决于最有利状态耗油率[14],即为(Nr/V)min,其关系为
| $ {L_{\max }} \approx \frac{{{{\overline {\zeta G} }_f}}}{{{C_e}{{({{\bar N}_{\rm{r}}}/V)}_{\min }}}} $ | (1) |
式中:V为飞行速度,Nr为需用功率,Ce为发动机单位耗油率,Gf为可用燃油量,ζ为功率利用系数。(Nr/V)min越小,Ce越小,对于一定的航程,Gf也越小。减少废阻功率及型阻功率可以降低(Nr/V)min,减少油耗提高功率利用率可以有效地改善航程。工程上航程的计算流程如下:
(1) 给定巡航高度,确定巡航飞行的燃油量
| $ {G_{{\rm{fu}}}} = {G_{{\rm{zhfu}}}}-\sum {\Delta {G_{{\rm{fu}}}}} $ | (2) |
式中:Gzhfu为总燃油量;∑Gfu是起飞,悬停,爬升,进入和退出航线,下滑至近地面,悬停落地,着陆余油和不可用燃油的总和,需根据具体机型而定,也可以按下列方法估计:
起飞,悬停及落地前悬停消耗的总燃油量按发动机最大状态耗油5 min计算;
下滑到近地面的耗油量是爬升进入航线耗油量的0.5~0.7倍;
着陆余油量按巡航飞行15 min(运输型)或30 min(旅客型)时间的耗油量计算。
(2) 确定巡航飞行的平均质量
由于巡航飞行的时间较长,燃油消耗量大,因此,从进入到退出航线直升机质量差别很大,为了计算的准确和方便,采用平均质量为宜。平均质量按式(3)计算
| $ {G_{{\rm{pi}}}} = {G_{{\rm{qf}}}}-\frac{{{G_{{\rm{fu}}}}}}{2}-\Delta {G_{{\rm{pfu}}}}-\Delta {G_{{\rm{qfu}}}} $ | (3) |
式中:Gpi是平均飞行质量;Gqf是直升机起飞质量;ΔGpfu是爬升进入航线耗油量;ΔGqfu是起飞悬停的耗油量。
(3) 按照需用功率计算模型,算出当前质量下不同飞行速度对应的需用功率,获得需用功率与速度的关系,画出Prs-V0曲线。
(4) 计算公里耗油率qkm
在需用功率曲线图上给出几个速度并分别查出Prs,根据Prs从发动机耗油特性曲线上查出qh,并按式(4)计算qkm
| $ {q_{{\rm{km}}}} - {q_{\rm{h}}}{\rm{/}}{V_0} $ | (4) |
作出qkm-V0曲线,在qkm-V0曲线上找出qkm值最小点,即为(qkm)min,此点对应的速度就是最大航程的远航速度Vcyh。
(5) 计算技术航程
| $ {L_0} = {G_{{\rm{fu}}}}/{({q_{{\rm{km}}}})_{\min }} $ | (5) |
(6) 计算实用航程
| $ L = {L_0} + \Delta {L_1} + \Delta {L_2} $ | (6) |
式中:ΔL1是起飞爬升进入航线的水平距离;ΔL2是退出航线下滑至地面的水平距离。
1.3 航时计算模型与流程(1) 确定续航高度并确定续航飞行的平均质量。
(2) 计算平飞的最小小时耗油量(qh)min
根据(Prs)min,查出发动机耗油特性曲线,即为直升机的最小小时耗油量(qh)min,对应的速度就是久航速度。
(3) 计算最大续航时间t
| $ t = \frac{{{G_{{\rm{fu}}}}}}{{{{({q_{\rm{h}}})}_{\min }}}} + \Delta {t_1} + \Delta {t_2} $ | (7) |
式中:Δt1是起飞爬升进入航线的留空时间;Δt2是退出航线下滑至地面的留空时间。通常Δt1+Δt2为6~8 min。
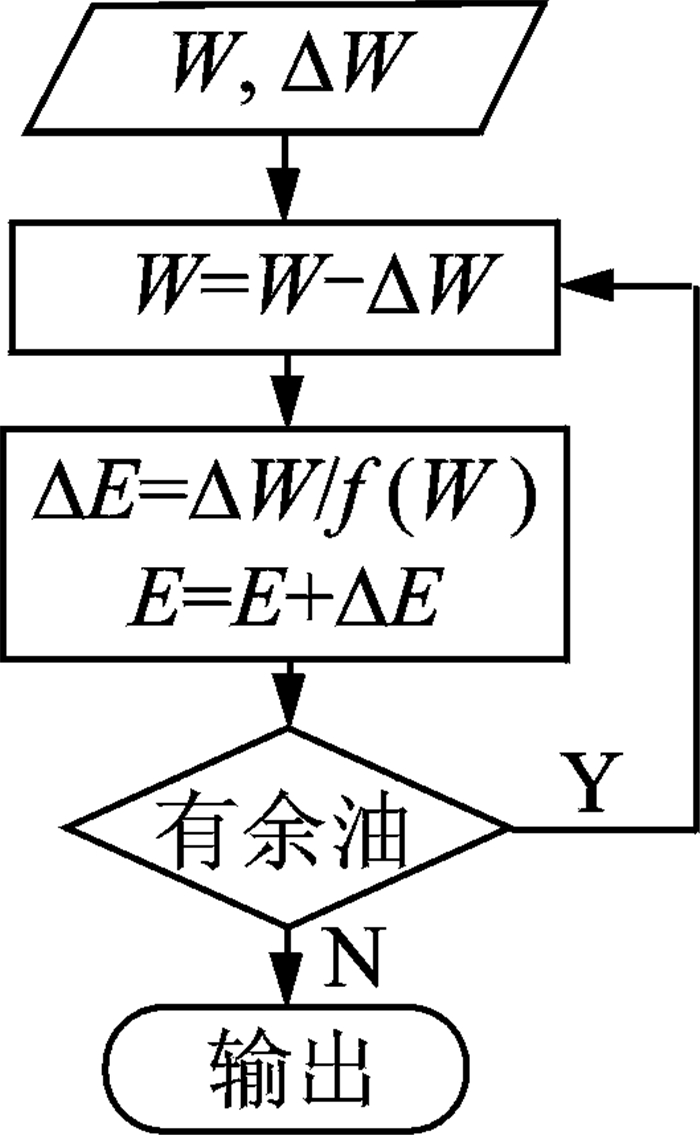
1.4 续航性能算例计算续航能力时使用对燃油质量进行离散的思想,考虑飞行过程中燃油质量变化的影响,假设油箱按直升机重心对称分布。计算直升机在不同质量情况下在给定高度和不同速度飞行时的需用功率,得到需用功率表,即得到需用功率随质量和速度的函数p(W, v),耗油率f(T, P)表达式根据某一飞行高度上的小时油耗表插值得到。续航时间计算简明流程如图 1所示,其中W为起飞质量,ΔW为计算步长,E为续航时间,f(W)为耗油率,与质量有关。航程的计算与上述续航时间计算流程类似。
|
图 1 直升机续航能力分析简明流程 Figure 1 Analysis flowchart of helicopter endurance performance |
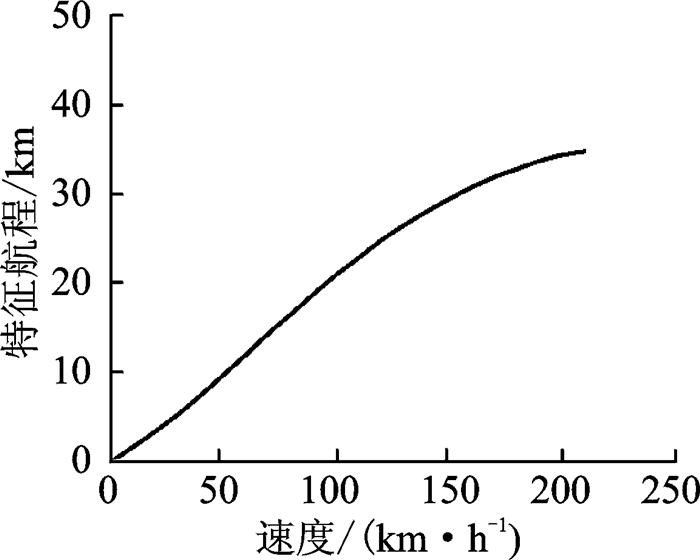
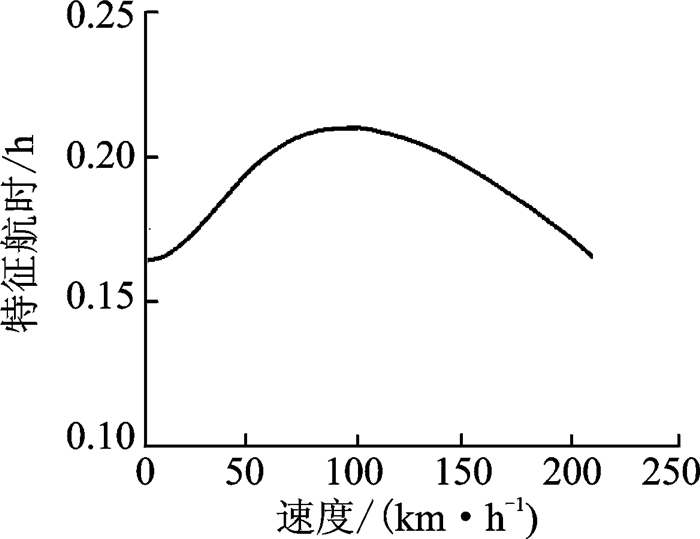
定义1%起飞质量的燃油能够持续的巡航时间为特征航时,1%起飞质量的燃油能达到的航程为特征航程。耗油率认为是高度、需用功率与温度的函数,通过分析得到起飞质量为2 200 kg时AC311型直升机的特征航程和特征航时随着飞行速度的变化曲线,如图 2,3所示。
|
图 2 特征航程(2 200 kg海平面) Figure 2 Specific range (2 200 kg sea level) |
|
图 3 特征航时(2 200 kg海平面) Figure 3 Specific endurance (2 200 kg sea level) |
可以看出,速度为230 km/h的特征航程最大,每消耗22 kg燃油能够飞行37.4 km;速度为90 km/h左右时特征航时最大,每消耗22 kg燃油能够续航13.2 min。
飞行过程中随着燃油的消耗,飞行质量在变化,相同转速和飞行速度对应的旋翼需用功率也随之变化。直升机为实现续航时间最长,要求不同质量下均以最小耗油率对应的速度飞行,类似地也可以得到最大航程的计算方法。以起飞质量为2 200 kg的AC311型直升机为例,假设完全消耗400 kg的燃油,理论上的最大续航时间为3.9 h,最大航程为701.2 km,此处未考虑发动机预热、起飞、盘旋等过程的燃油消耗。
2 优化转速旋翼续航性能分析通过对不同飞行质量、不同飞行高度、不同飞行速度下、不同旋翼转速下的功率计算,选取各种飞行状态下需用功率最小的转速作为最优转速,进一步计算旋翼转速优化时对续航性能的影响。
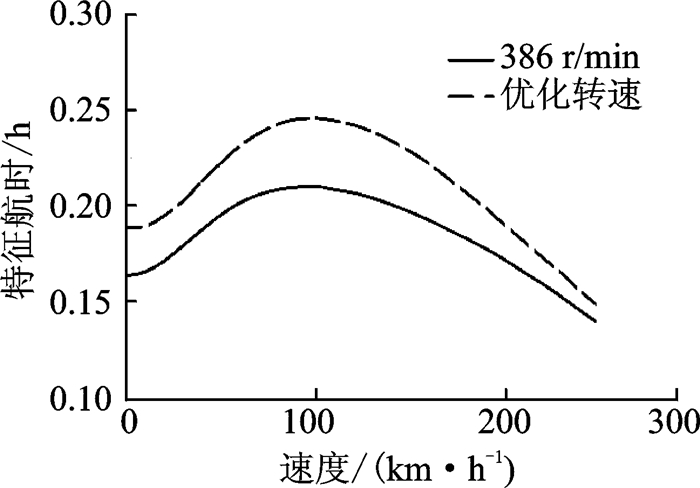
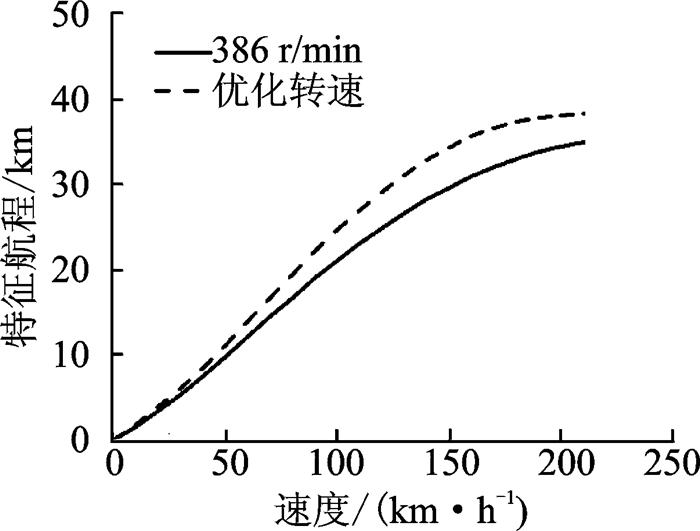
分别在额定转速和优化转速下,分析得到起飞质量为2 200 kg、海平面标准大气下特征航程与特征航时随飞行速度的变化曲线,如图 4,5所示。可以看出,100 km/h速度时的特征航时最大,优化转速比额定转速工作的续航时间提高了15.8%。220 km/h速度的特征航程最大,优化转速比额定转速的工作航程提高了7.9%。
|
图 4 优化转速与额定转速特征航时对比 Figure 4 Comparison of specific endurance between optimum rotating speed and rated rotating speed |
|
图 5 优化转速与额定转速特征航程对比 Figure 5 Comparison of specific range between optimum rotating speed and rated rotating speed |
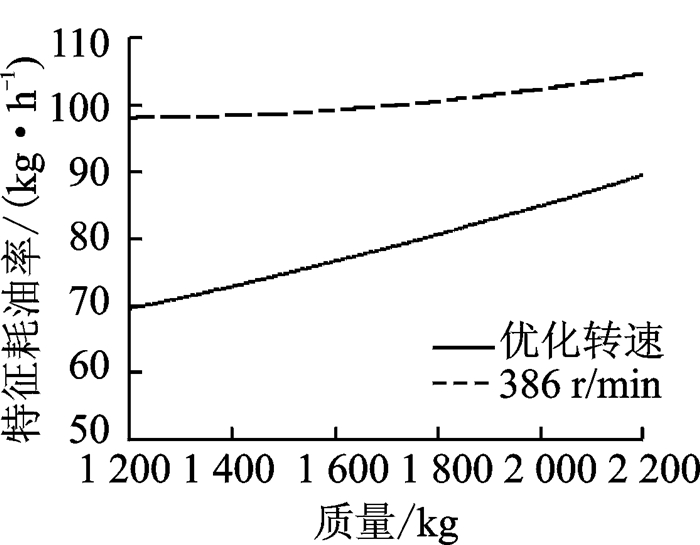
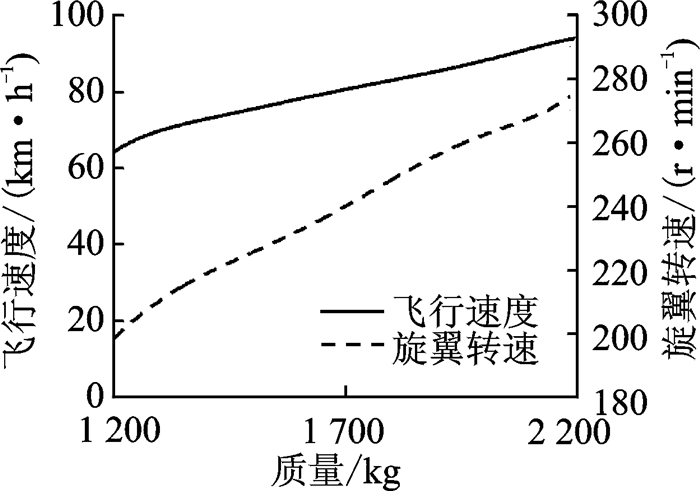
在飞行过程中随着燃油的消耗,旋翼需用功率随之变化。以额定转速和优化转速工作时,不同质量对应的最小耗油率如图 6所示,可见质量对耗油率的影响较大,随着质量的降低,采用优化转速的耗油率减少得越多,质量为2 200 kg时,耗油率降低14.45%,质量为1 800 kg时,耗油率降低19.88%,质量为1 200 kg时,耗油率降低29.05%。通过不同质量、不同速度、不同转速的组合计算,可以获得特征航时最长的点对应的飞行速度和转速,按照图 7中的飞行速度与转速方案能够使直升机在不同质量下燃油消耗量最小,此时续航时间最长。
|
图 6 优化转速与额定转速耗油率对比 Figure 6 Comparison of fuel consumption rate between optimum rotating speed and rated rotating speed |
|
图 7 不同质量和速度下的优化转速 Figure 7 Optimum speed with different masses and rotating speeds |
假如不考虑进入、退出航线和不可用余油等影响,考虑飞行过程中质量的动态变化,按照400 kg燃油计算,采用优化转速的最大航时是4.7 h,比额定转速的航时提高了20.5%。当燃油质量达到1 000 kg时,按优化转速工作的最大续航时间提高到12.7 h,而按额定转速工作最大续航时间只能达到10.0 h,提高了27%,如表 1所示,燃油越多,旋翼转速优化后的续航时间提高得越明显。
| 表 1 旋翼优化转速对续航时间的影响 Table 1 Effect of rotor optimum rotating speed for endurance |
3 旋翼变速策略分析
虽然优化旋翼转速可以显著提高航程和航时,但是连续的转速变化对于变速机构的设计要求较高,因此通过有限级的变速比来设置多挡旋翼转速,具有更现实的工程意义。
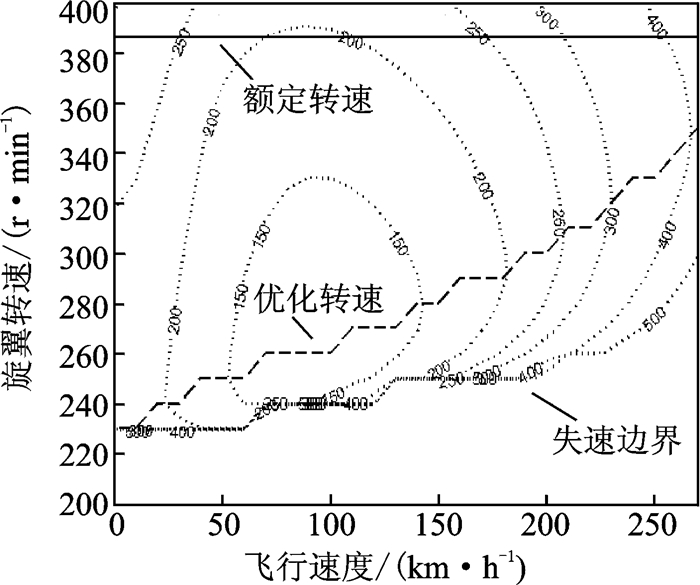
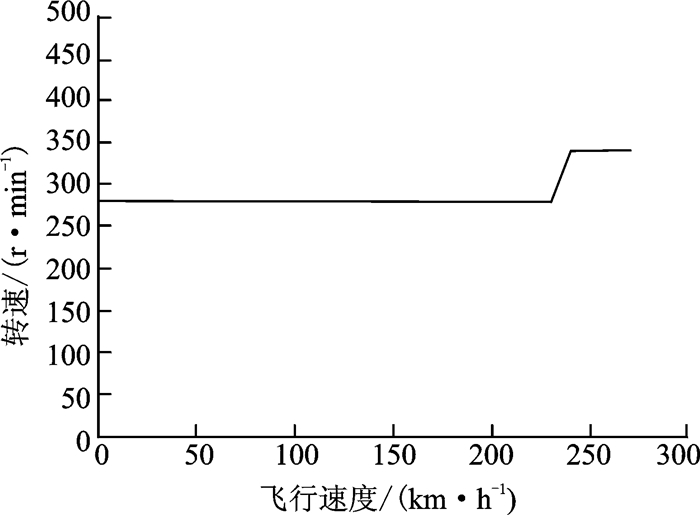
3.1 旋翼的一级变速分析续航时间与旋翼转速、总质量和飞行高度有关,这里以0 m高度海平面任务剖面为典型算例,分析旋翼变速策略。对于2 000 kg总质量、海平面高度的情况,加入旋翼转速的变化,计算得到的需用功率曲线如图 8所示(图中等值线上标注的是为需用功率值)。需用功率最低的转速大概在230 r/min与340 r/min之间。通过约束条件的调整,放宽旋翼保持某一转速时飞行速度的取值范围,就可减少旋翼转速的变化次数,得到一级变速的两档转速。选取280 r/min作为一级变速时的一个转速,为了兼顾直升机大速度飞行(大于250 km/h)时的情况,此时280 r/min已经失速,选取大速度飞行时的一个最优转速340 r/min作为另一个转速,则一级变速设定规律如图 9所示。
|
图 8 需用功率及最优转速分析曲线 Figure 8 Contours of demand power and optimal rotating speed |
|
图 9 一级变速时旋翼转速配置 Figure 9 Rotor rotating speed configuration of level 1 variable speed |
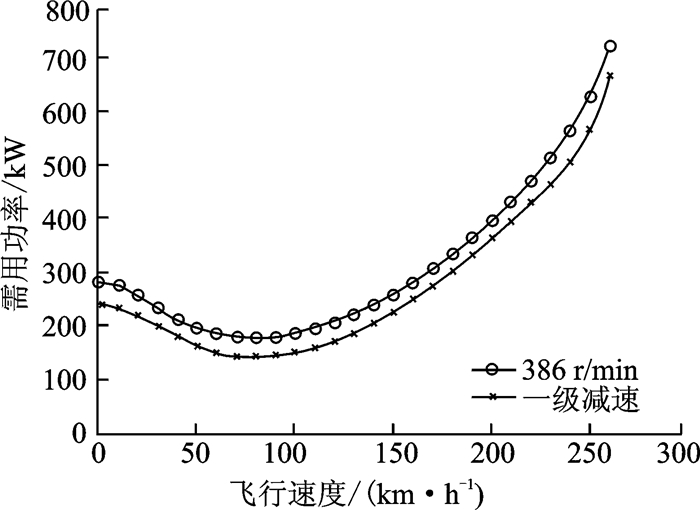
图 10为一级变速和386 r/min额定转速的需用功率比较图,可以看出,在飞行速度较低的情况下,采用一级变速的方案可以节省较大比例的需用功率,当平飞速度较大时,由于废阻功率占据需用功率的比例越来越大,节省功率的百分比将会减小。
|
图 10 额定转速与一级变速需用功率对比 Figure 10 Demand power comparison of rated speed and level 1 variable speed |
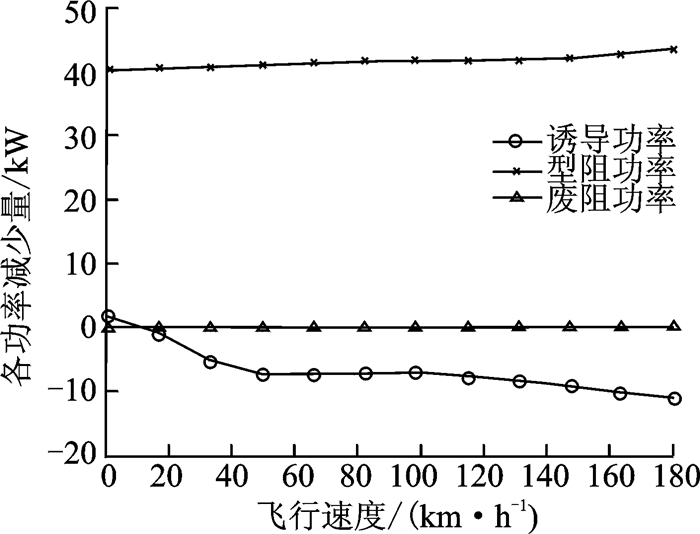
图 11是一级变速相对386 r/min额定转速,诱导功率、型阻功率和废阻功率减少量随飞行速度的变化趋势图。从图中可以看出,随飞行速度增大,采用一级变速可以明显降低旋翼的型阻功率,对废阻功率影响较小,诱导功率则略有增加。
|
图 11 一级变速相对额定转速各部分功率减少量 Figure 11 Power decrement between level 1 variable rotating speed and rated rotating speed |
3.2 旋翼的二级变速分析
由于直升机的质量在飞行中一直变化,并且质量和飞行速度对于最优转速存在显著影响,因此需要综合飞行质量、飞行速度和配平限制得到二级变速的设计方案。
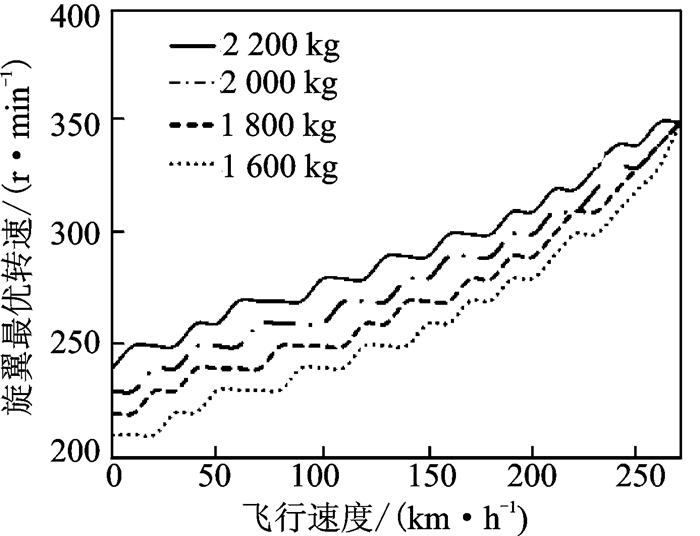
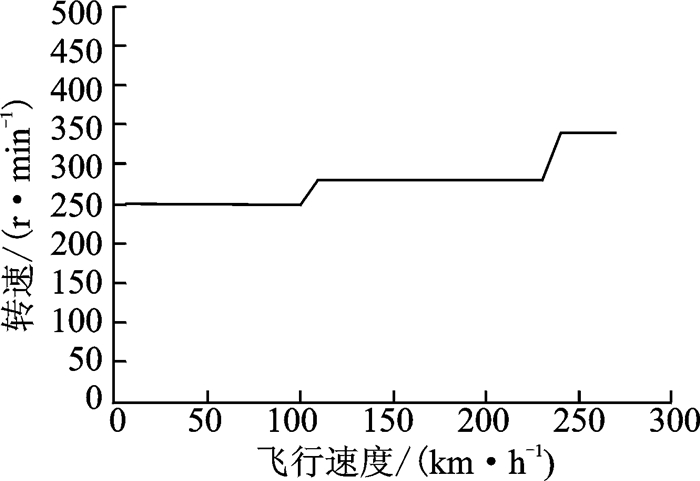
图 12是不同起飞质量下的最优转速选取与飞行速度的关系(都处于海平面的高度),放宽旋翼保持某一转速时飞行速度的取值范围,就可从无级变速得到二级变速。100 km/h以内的飞行速度取最优转速250 r/min作为第一级转速;大速度飞行时采用最优转速340 r/min作为最高转速,保证直升机在大速度飞行下的性能;至于中间的转速,选取飞行速度在100~200 km/h之间较为优化的转速280 r/min作为另一个转速,最后的旋翼转速配置见图 13。
|
图 12 不同起飞质量时旋翼最优转速方案 Figure 12 Rotor optimal rotating speed scheme with different masses |
|
图 13 二级变速时旋翼转速配置 Figure 13 Rotor rotating speed configuration of level 2 variable speed |
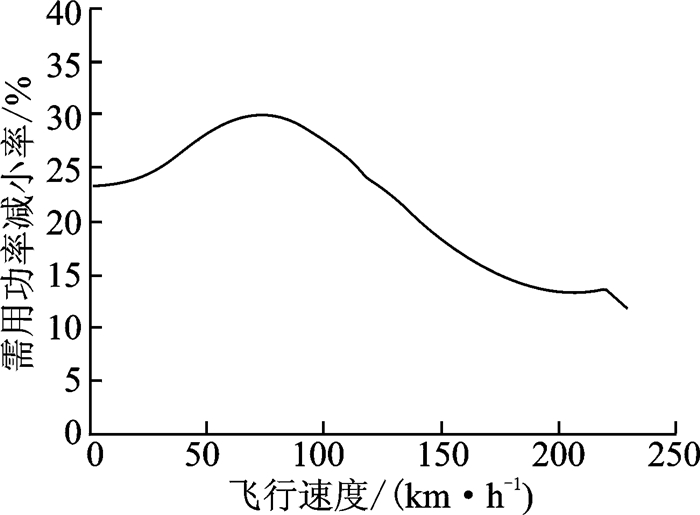
图 14为二级变速条件下需用功率的减少率,可以看出二级变速下与386 r/min额定转速相比减少量很大,最大减少率达30%左右,效果十分明显。
|
图 14 二级变速相对额定转速需用功率减少量(1 600 kg海平面) Figure 14 Power decrement between level 2 variable rotating speed and rated rotating speed (1 600 kg sea level) |
3.3 一级变速与二级变速对比
以起飞质量2 t并携带1 t燃油的AC311型直升机为例,分析结果如表 2所示,在海平面二级变速情况下航时能达到13.09 h,相比386 r/min额定转速情况下的10.21 h,航时增加了2.88 h。而相比一级变速下的12.90 h,航时仅增加了0.19 h,增加效果不是很明显。
| 表 2 有级变速方案及其航时效果对比 Table 2 Step change speed schemes and the comparison of endurance |
通过计算分析,二级变速与一级变速相比需用功率减少量不是很大,减少率均在5%以内,二级变速效果相对于一级变速不是很明显。结合变速机构实现的成本,一级变速是更有效的提高航时的工程手段。
4 结论本文以AC311直升机为例,建模分析了直升机续航性能,评估了旋翼变转速对续航性能的影响,得出如下结论:
(1) 飞行过程中随着燃油的消耗,相同转速和飞行速度对应的旋翼需用功率也随之变化,直升机为实现续航时间最长,要求不同质量下均以最小耗油率对应的速度飞行,最大航程亦然。
(2) 合理的优化旋翼转速,可以显著提高直升机续航性能;全机质量越轻,优化转速的耗油率减少得越多,随着燃油消耗,优化转速对续航性能的提升越明显。
(3) 旋翼有限级变速(一级、二级)和额定转速比较,可以显著减小其型阻功率,从而提高续航性能;二级变速相对于一级变速,旋翼需用功率减小的不多(不超过5%),考虑到多级变速实现成本,一级变速是更有效的提高续航性能的工程手段。
| [1] |
JASON H S, FARHAN G. An investigation of variable speed rotor RPM on performance and trim[C]//American Helicopter Socirty 64th Annual Forum Proceedings. Montreal:AHS International, 2008:697-705. |
| [2] |
PROUTY R W.
Should we consider variable rotor speeds[J]. Vertiflite, 2004, 50(4): 24–27.
|
| [3] |
KAREM A E. Optimum speed rotor:U.S. Patent, No. 60/072, 98[P]. 1999. |
| [4] |
STEIHER J H. An investigation of performance benefits and trim requirements of a variable speed helicopter rotor[D]. USA:The Pennsylvania State University, 2008. |
| [5] |
GUO W. Flight control design for rotorcraft with variable rotor speed[D]. USA:The Pennsylvania State University, 2009. |
| [6] |
DIOTTAVIO J, FRIEDMANN D. Operational benefits of an optimal, Widely variable speed rotor[C]//Proceedings of the American Helicopter Society 66th Annual Forum 2010. USA:[s.n], 2010. |
| [7] |
BERRY B, CHOPRA I. Wind tunnel testing for performance and vibratory loads of a variable-speed Mach-scalerotor[C]//American Helicopter Society 67th Annual Forum. Virginia:[s.n.], 2011:1227-1240. |
| [8] |
GRAHAM B D, CHOPRA I. Aeromechanics of a variable speed rotor[C]//American Helicopter Society 67th Annual Forum Proceedings. Virginia:AHS International, 2011:1058-1073. |
| [9] |
ANUBHAV D, HYEONSOO Y, THOMAS R. Experimental investigation and fundamental understanding of a slowed UH-60A rotor at high advance ratios[C]//American Helicopter Society 67th Annual Forum. Virginia:[s.n], 2011:1105-1130. |
| [10] |
韩东.
变转速旋翼直升机性能及配平研究[J]. 航空学报, 2013, 34(6): 1241–1248.
HAN Dong. Study on the performance and trim of a helicopter with a variable speed rotor[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1241–1248. |
| [11] |
徐明, 韩东, 李建波.
变转速旋翼气动特性分析及试验研究[J]. 航空学报, 2013, 34(6): 2047–2056.
XU Ming, HAN Dong, LI Jianbo. Analysis and experimental investigation on the aerodynamic characterisitics of variable speed rotor[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 2047–2056. |
| [12] |
HAN Dong, WANG J.
Transient loads control of a variable speed rotor during lagwise resonance crossing[J]. AIAA Journal, 2013, 51(1): 20–29.
DOI:10.2514/1.J050598
|
| [13] |
YEO H, BOUSMAN W G, JOHNSON W.
Performance analysis of a utility helicopter with standard and advanced rotors[J]. Journal of the American Helicopter Society, 2005, 45(3): 250–270.
|
| [14] |
JOHNSON W. Helicopter theory[M].New York:Dover Publications, Inc., 1980:45-52. |
 2018, Vol. 50
2018, Vol. 50


