多架直升机共同执行飞行任务时,由于直升机留空时间相对较短,为了保证足够的任务时间,往往需要多架直升机同时起降或以尽可能短的时间间隔高效率起降。另一方面,在繁忙的起降场地可能存在多架直升机同时起飞/降落的情形。如果起降场地有限,比如可搭载多架直升机的舰船的起降甲板,则直升机间距离相对较近,其旋翼下洗流可能会存在相互干扰,从而影响到直升机的起降安全。美国V-22“鱼鹰”就曾遇到过受迎风方向正在降落直升机气动干扰后发生不可控滚转的问题[1]。因此,开展直升机旋翼之间下洗流气动干扰研究,对于在有限的起降场地上多架直升机进行安全、高效率起降具有十分重要的意义。
国外针对多机气动干扰问题采用试验方法和数值仿真方法开展了一定的研究工作。文献[2]通过风洞试验研究了两架V-22旋翼之间的气动干扰,分析了其间距等参数对旋翼间气动干扰的影响,可以为V-22多机飞行或起降设计提供指导。文献[1]中分别采用粒子图像测速(Particle image velocimetry, PIV)试验和动量源方法研究了CH-46直升机尾迹对V-22的气动干扰,但其动量源方法采用了不可压流动及层流假设,与真实的旋翼流动具有一定的差异。文献[3~5]采用基于半经验模型的尾迹方法研究了多机气动干扰问题。目前国内主要针对倾转旋翼机、共轴双旋翼直升机、纵列双旋翼直升机等具有多副旋翼的同一架直升机/旋翼机的旋翼之间的气动干扰问题开展了试验和数值仿真研究[6-12],但对多机气动干扰问题的研究很少。由于多机气动干扰风洞试验难度大、周期长、成本高,而尾迹类方法和动量源方法对流场细节等的模拟均存在一定的困难。因此,开展多机气动干扰计算流体力学(Computational fluid dynamics, CFD)模拟研究具有十分重要的意义。
本文采用基于运动嵌套网格技术的CFD方法,开展多机起降旋翼间气动干扰研究,对地效作用下旋翼之间的气动干扰进行了数值模拟,分析了其干扰机理,并研究了旋翼间距、环境风速对其干扰的影响,得出了一些有参考价值的结论。
1 网格生成与数值方法 1.1 网格生成由于直升机在飞行过程中,旋翼桨叶同时进行旋转、周期挥舞、周期变距等运动,采用了运动嵌套网格方法对桨叶复杂运动边界进行处理。网格生成步骤如下:
步骤1 对桨叶进行贴体结构网格划分,并在桨叶表面及桨尖附近进行了加密以提高流场捕捉精度。单片桨叶网格单元数约为114万。
步骤2 采用笛卡尔网格划分技术生成背景网格。为了提高旋翼气动干扰的模拟精度,获得高精度的气动干扰特性,在两副旋翼区域及其中间区域进行了加密。同时,为了提高嵌套边界流场信息传递精度,在网格划分过程中尽量保持背景网格在嵌套区域几何尺寸与桨叶网格接近。本文将舰/地面简化为了直至远场的平面,以初步研究舰/地面对旋翼间气动干扰的影响,并对网格进行加密,以提高近舰/地面流场模拟精度。背景网格单元数约为1 700万。
步骤3 采用距离加权平均方法进行嵌套边界区域流场信息插值,从而实现桨叶网格与背景网格流场信息的传递。
计算网格如图 1所示。

|
图 1 计算网格 Figure 1 Computational grid |
1.2 数值方法
采用任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerian, ALE)形式的非定常Navier-Stokes方程作为含有运动边界黏性流动的控制方程,其积分守恒型形式如下
| $ \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{W}}{\rm{d}}\mathit{\Omega }} + \int_\mathit{s} {({\mathit{\boldsymbol{F}}_c}-\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{v}}_g}-{\mathit{\boldsymbol{F}}_v})} \cdot {\rm{d}}s = 0 $ | (1) |
式中:W为守恒变量,Fc和Fv分别为对流通量和黏性通量,vg为网格运动速度。
采用数值离散技术对式(1)求解,关键技术如下:
(1) 低速预处理技术。由于旋翼流场中不可压缩流与可压缩流共存,因此,采用低速预处理技术以改善低速流动收敛性,并提高计算精度。低速预处理后的式(1)可表述为
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}\mathit{\Omega }} + \int_\mathit{s} {({\mathit{\boldsymbol{F}}_c}-\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{v}}_g}-{\mathit{\boldsymbol{F}}_v})} \cdot {\rm{d}}s = 0 $ | (2) |
式中:Q为原始变量,Γ为预处理矩阵。
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} = }}\left[{\begin{array}{*{20}{c}} \mathit{\Theta }&0&0&0&{{\rho _T}}\\ {{\mathit{\Theta }_u}}&\rho &0&0&{{\rho _T}u}\\ {{\mathit{\Theta }_v}}&0&\rho &0&{{\rho _T}v}\\ {{\mathit{\Theta }_w}}&0&0&\rho &{{\rho _T}w}\\ {\mathit{\Theta }H-1}&{\rho u}&{\rho v}&{\rho w}&{{\rho _T}H + \rho {C_P}} \end{array}} \right] $ | (3) |
式中:
(2) 空间离散。对流通量的计算采用Roe格式,并结合解的重构以达到二阶精度。黏性通量的计算采用二阶中心格式。
(3) 时间离散。由于旋翼流场为非定常流场,采用双时间步时间推进以获得时间精确解,表达式为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\int_\mathit{\Omega } {\mathit{\boldsymbol{W}}{\rm{d}}\mathit{\Omega }} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\frac{\partial }{{\partial \tau }}\int_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}\mathit{\Omega }} + \\ \int_\mathit{s} {({\mathit{\boldsymbol{F}}_c}-\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{v}}_g}-{\mathit{\boldsymbol{F}}_v})} \cdot {\rm{d}}s = 0 \end{array} $ | (4) |
采用隐式三点向后差分格式对式(4)进行离散。时间离散精度为二阶。
(4) 湍流模型。湍流模型采用两方程的SST k-ω模型。
(5) 加速收敛措施。采用基于Gauss-Seidel迭代的多重网格技术以提高收敛速度。
1.3 数值方法验证以Caradonna & Tung旋翼和AH-1G直升机1:7模型旋翼为例,验证了本文数值方法的可靠性。图 2给出了Caradonna & Tung旋翼无升力前飞状态方位角ψ分别为30°和120°时,0.893R(R为旋翼半径)剖面压力系数计算值与试验值[13]的对比。悬停桨尖马赫数为0.8,前进比为0.2,轴倾角为0°,0.75R剖面总距为0°。从图中可以看出,计算结果与试验结果吻合良好。

|
图 2 Caradonna & Tung旋翼计算结果与试验结果对比 Figure 2 Computed and experimental chordwise pressure coefficient for Caradonna & Tung rotor |
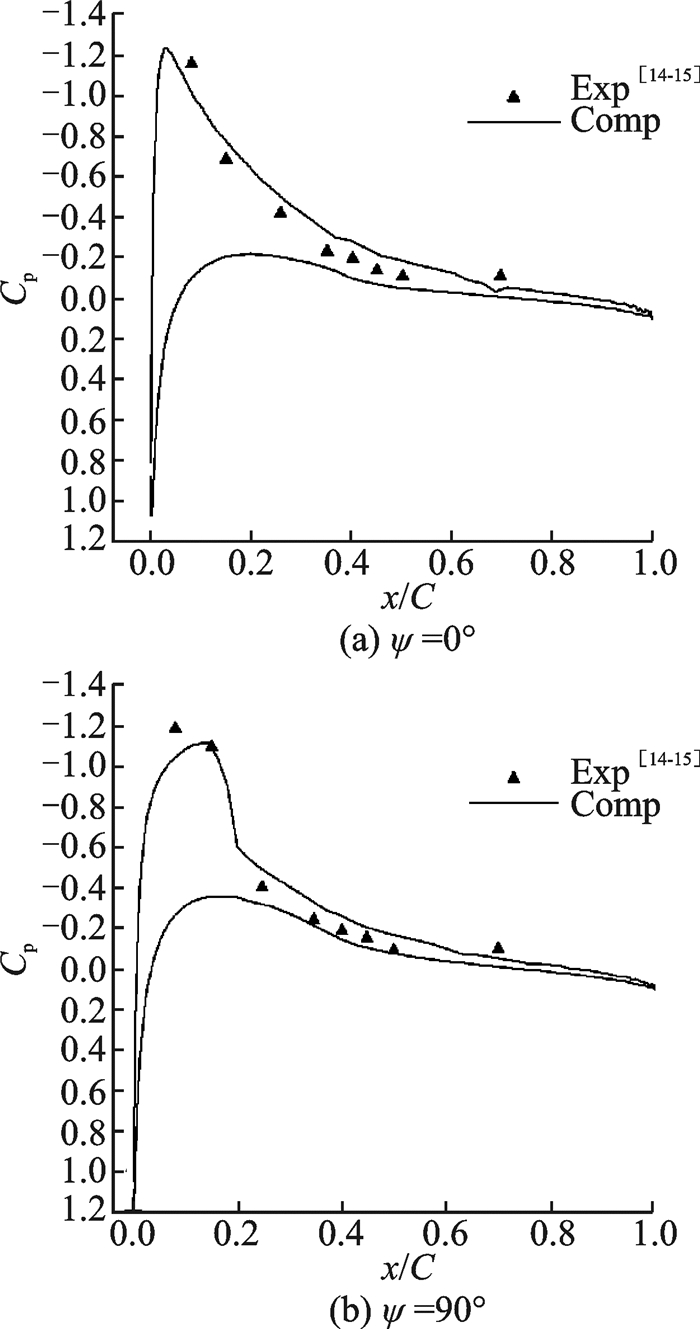
图 3给出了AH-1G直升机1:7模型旋翼前飞状态方位角ψ分别为0°和90°时,0.995R剖面压力系数计算结果与试验结果[14-15]的对比。悬停桨尖马赫数为0.664,前进比为0.164,轴倾角为0°。配平数据为:θ=6.14+0.9cosψ-1.39sinψ,β=0.5-cosψ。其中总距θ为0.75R剖面总距。从图中可以看出,计算结果与试验结果吻合良好。而计算得到的旋翼拉力系数为0.005 59,与试验值0.005 4也较为吻合。
|
图 3 AH-1G模型旋翼计算结果与试验结果对比 Figure 3 Computed and experimental chordwise pressure coefficient for AH-1G model rotor |
2 结果分析 2.1 两架直升机旋翼之间气动干扰分析
以两架相同直升机旋翼为对象,研究了旋翼之间的气动干扰,每副旋翼均包含3片桨叶。两副旋翼桨毂中心处于同一高度,均离舰/地0.561R;两副旋翼处于顺风向前后位置,间距(桨毂中心间距)为3R。环境风速为0.069 4Vtip(Vtip为旋翼桨尖速度),即旋翼的前进比为0.069 4。采用尾迹方法进行旋翼配平,以作为旋翼流场CFD计算的输入。虽然本文重点研究旋翼下洗流之间的气动干扰,并未考虑机身尾流的影响,但为了更接近真实的起降气动环境,旋翼配平采用了全机配平。
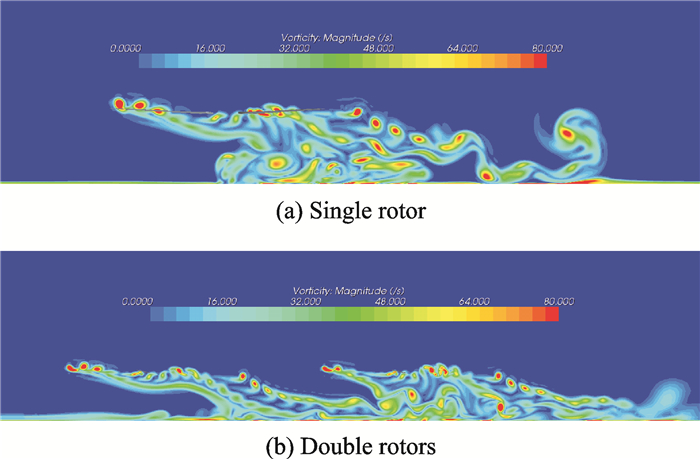
图 4给出了顺风向通过桨毂中心的竖直剖面单副旋翼及两副旋翼气动干扰下的涡量云图。为方便起见,在旋翼气动干扰分析中,上风位置旋翼称为旋翼1,下风位置旋翼称为旋翼2。从图中可以看出,单副旋翼情形,旋翼产生的尾涡在下洗作用及来流的影响下向桨盘斜下方运动,并在舰/地面附近形成了较为紊乱的涡流区。两副旋翼气动干扰下,与单旋翼不同,旋翼1桨盘下方、舰/地面附近涡的范围减小,强度降低,并向旋翼2方向偏移。旋翼1后侧的尾涡在向后下方运动过程中,其垂向位置相对于单旋翼情形向下偏移,并在旋翼2下方与旋翼2的尾涡交汇。相对于单旋翼情形,两副旋翼尾涡交汇以后相互影响,在旋翼2下方形成了更强的涡。
|
图 4 顺风向通过桨毂中心竖直剖面涡量图 Figure 4 Vorticities on vertical section pass through rotor hubs and along wind direction |
为了更好地研究旋翼尾涡的运动与发展,采用Q准则进行了涡识别。图 5给出了单旋翼情形及两副旋翼气动干扰下的Q准则空间等值面。从图中可以看出,单旋翼情形,旋翼尾涡自桨叶脱落,运动到舰/地面附近后形成了较为紊乱的涡流区。而两副旋翼气动干扰下,旋翼1的尾涡并未形成单旋翼情形下的紊乱的涡流区,而是在沿流向相对较远的范围内保持着清晰的涡结构,这也与图 4的剖面涡量图一致。另一方面,直升机在前飞过程中,桨叶在90°方位角和270°方位角会形成较强的桨尖涡,并向后下方运动,图 5(a)也体现了这一点。但两副旋翼气动干扰下,旋翼1在90°方位角和270°方位角形成的桨尖涡在向后运动的过程中受旋翼2的干扰,向外偏移。相应的,旋翼1其他方位角下形成的桨尖涡向后运动过程中在水平面内沿横向也有所延伸。旋翼2在90°方位角形成的桨尖涡受旋翼1的影响,强度有所减弱,而在270°方位角形成的桨尖涡则与旋翼1的桨尖涡交汇并融合。

|
图 5 Q准则空间等值面 Figure 5 Isosurface of Q-criterion |
表 1给出了两副旋翼的升力系数CL和扭矩系数CT相对于单旋翼情形的对比。从表中可以看出,旋翼1的升力系数和扭矩系数均与单旋翼情形基本相当;而旋翼2的升力系数相对于单旋翼情形约降低1.80%,扭矩系数则大幅增加,约增加8.56%。计算结果表明,旋翼之间的气动干扰对下风位置旋翼的影响明显高于上风位置旋翼,会造成其升力系数降低,扭矩系数增加。
| 表 1 旋翼升力系数与扭矩系数 Table 1 Lift coefficients and torque coefficients for rotors |
2.2 旋翼间距对旋翼之间气动干扰的影响
考虑旋翼间距对旋翼之间的气动干扰的影响,图 6给出了旋翼间距分别为2.5R和4R时通过桨毂中心的剖面涡量图,环境风速为0.069 4Vtip。从图中可以看出,旋翼间距对旋翼1桨盘下方尾涡的影响较小,对旋翼2桨盘下方尾涡的影响相对较大。2.5R间距下,旋翼1后侧的尾涡在垂向上以更高的位置进入与旋翼2尾涡的交汇区。顺风向,两者交汇的位置相对于旋翼2桨毂中心向前偏移。旋翼1的尾涡在随风向后运动过程中,随着距离的增加,其强度有所降低。因此,大的旋翼间距下,旋翼1和旋翼2尾涡交汇以后,在旋翼2下方形成的涡流的强度有所降低。

|
图 6 不同旋翼间距下顺风向通过桨毂中心竖直剖面涡量图 Figure 6 Vorticities on vertical section pass through rotor hubs along wind direction with different rotor distances |
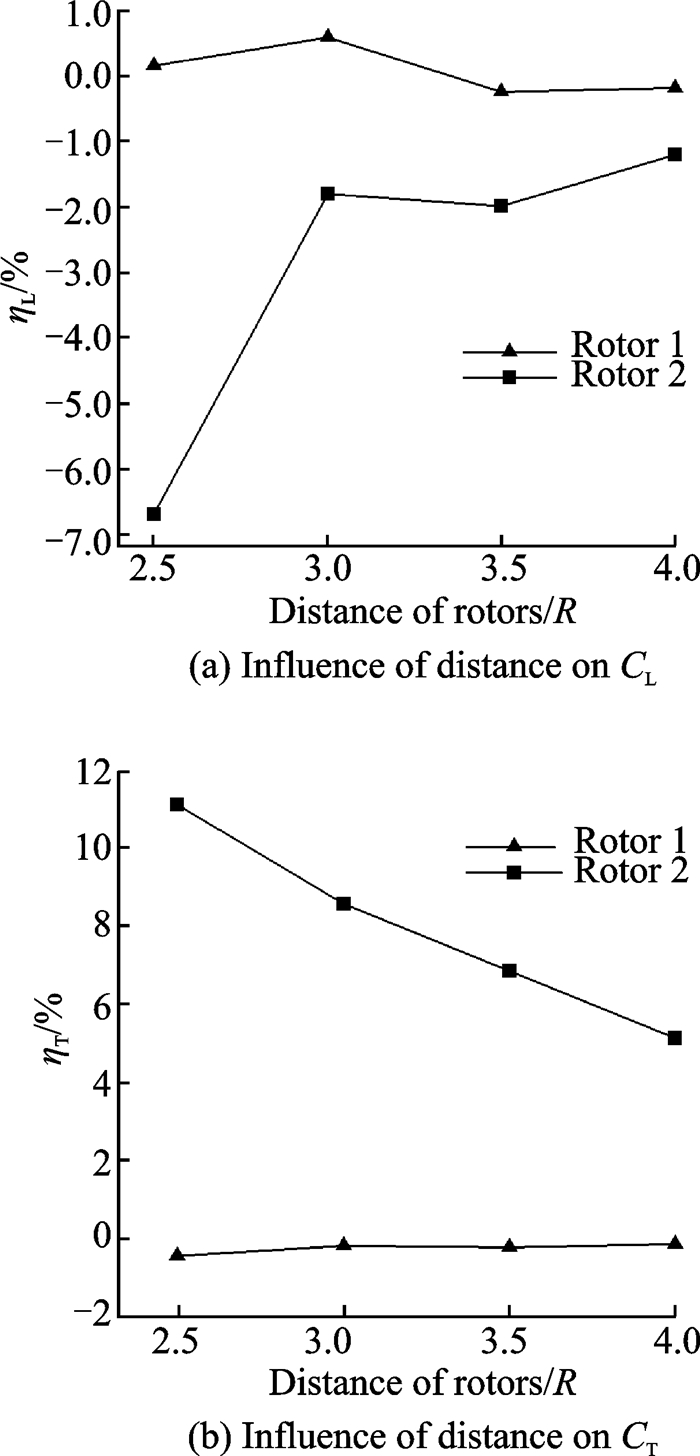
图 7给出了旋翼间距对旋翼1和旋翼2的升力系数CL、扭矩系数CT相对于单旋翼情形的影响(ηL, ηT)。从图中可以看出,旋翼间距对旋翼1的升力系数和扭矩系数的影响均较小,在1%以内。2.5R间距下,旋翼2的升力系数明显降低,约降低6.68%;3R~4R间距范围内,气动干扰对旋翼2升力系数的影响大幅降低,其升力系数相对于单旋翼情形降低1%~2%;在2.5R~4R间距范围内,气动干扰导致旋翼2的扭矩系数明显增加,其中2.5R间距下,旋翼2的扭矩系数约增加了11.10%。随着间距的增加,气动干扰对旋翼2扭矩系数的影响明显降低。
|
图 7 旋翼间距对旋翼升力系数和扭矩系数的影响 Figure 7 Influence of rotor distances on lift coefficients and torque coefficients |
2.3 环境风速对旋翼之间气动干扰的影响
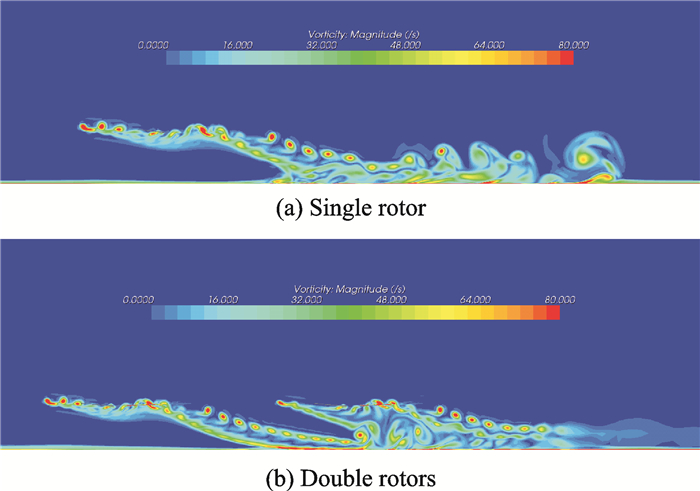
考虑环境风速对旋翼之间气动干扰的影响,图 8给出了环境风速为0.088 0Vtip时桨毂中心剖面涡量图。计算结果表明,相对于0.069 4Vtip环境风速,随着环境风速的提高,旋翼1尾涡与单旋翼情形趋于一致,对旋翼2尾涡的影响相对较大。
|
图 8 环境风速0.088 0Vtip时为顺风向通过桨毂中心竖直剖面涡量图 Figure 8 Vorticities on vertical section pass through rotor hubs along wind with 0.088 0Vtip |
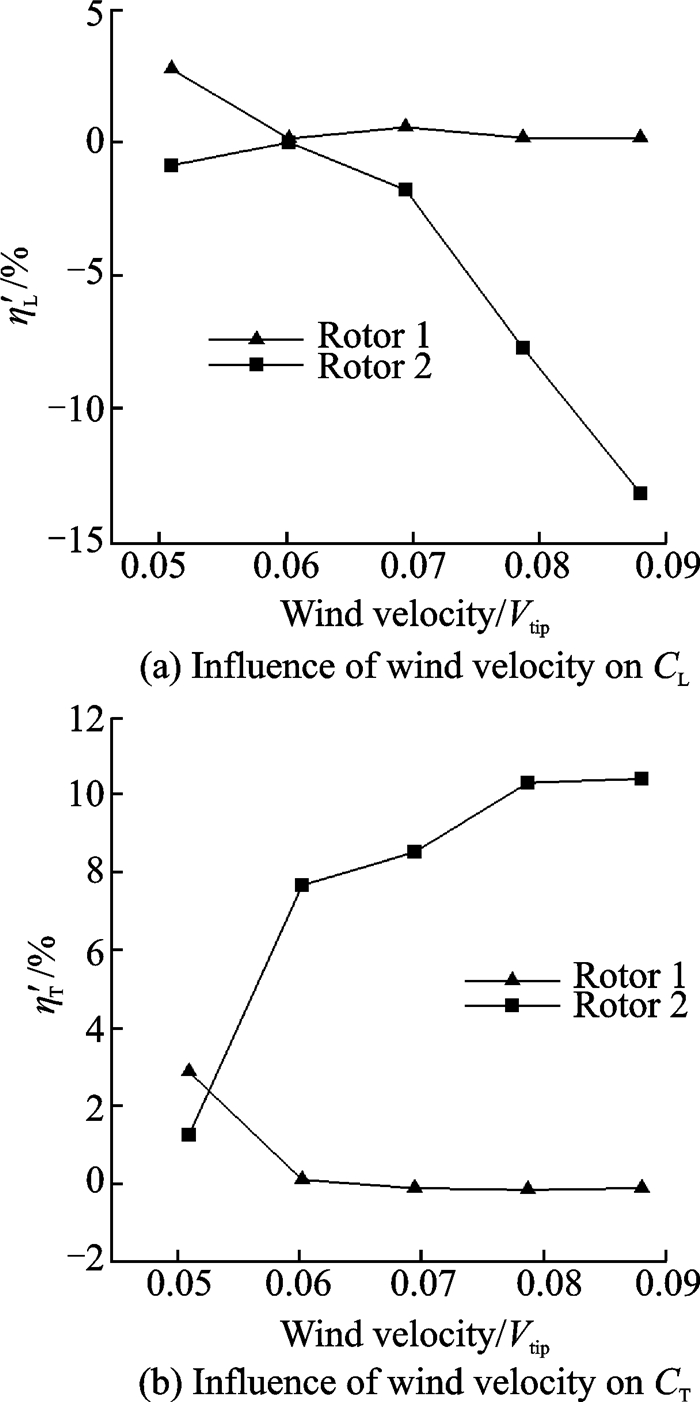
图 9给出了环境风速对旋翼1和旋翼2的升力系数CL、扭矩系数CT相对于单旋翼情形的影响(η′L, η′T)。从图中可以看出,环境风速为0.050 9Vtip时,旋翼1的升力系数约增加了2.74%,扭矩系数约增加了2.85%;环境风速大于0.060 2Vtip时,旋翼1的升力系数和扭矩系数与单旋翼情形基本一致。环境风速小于0.060 2Vtip时,旋翼2的升力系数与单旋翼情形较为接近;环境风速大于0.069 4Vtip时,旋翼2的升力系数相对于单旋翼情形迅速降低,其中在环境风速为0.088 0Vtip时,升力系数约降低了13.18%。旋翼2的扭矩系数相对于单旋翼情形,随着环境风速的增加而迅速增加,其中在环境风速为0.088 0Vtip时,扭矩系数约增加了10.46%。计算结果表明,随着环境风速的增加,气动干扰对旋翼1的影响相对较小,而对旋翼2的影响较为明显,会导致旋翼2升力系数降低,扭矩系数增加。
|
图 9 环境风速对旋翼升力系数和扭矩系数的影响 Figure 9 Influence of wind velocities on lift coefficients and torque coefficients |
3 结论
以两架直升机旋翼之间的气动干扰为研究对象进行了数值模拟,重点研究了不同旋翼间距、环境风速对旋翼间气动干扰的影响,得到如下结论:
(1) 旋翼之间的气动干扰对上风位置旋翼的影响相对较小;但对下风位置旋翼有显著影响,会导致下风位置旋翼的升力系数降低,扭矩系数增加。
(2) 较小旋翼间距下,旋翼之间的气动干扰会导致下风位置旋翼的升力系数明显降低。而随着旋翼间距的增加,对下风位置旋翼的升力系数和扭矩系数的影响会明显降低。
(3) 随着环境风速的增加,气动干扰对下风位置旋翼的不利影响迅速增加,会导致下风位置旋翼的升力系数迅速降低,扭矩系数迅速增加。
综上,多机起降时,下风位置直升机应当适当提高总距,或与上风位置直升机保持合适的距离。
| [1] |
RAJAGOPALAN G, NIAZI S, WADCOCK A J, et al. Experimental and computational study of the interaction between a tandem-rotor helicopter and a ship[C]//Proceedings of the American Helicopter Society 61st Annual Forum. Grapevine, USA:the American Helicopter Society International, 2005. |
| [2] |
YAMAUCHI G K, WADCOCK A J, DERBY M R. Measured aerodynamic interaction of two tiltrotors[C]//Proceedings of the American Helicopter Society 59th Annual Forum. Phoenix, USA:the American Helicopter Society International, 2003. |
| [3] |
YEMENICI O, UZOL N S, UZOL O. Investigation of rotor-rotor interactions for two helicopters in forward flight using free-vortex wake methodology[R]. AIAA 2010-4558, 2010. |
| [4] |
HE Chengjian, XIN Hong, BHAGWAT M. Advanced rotor wake interference modeling for multiple aircraft shipboard landing simulation[C]//Proceedings of the American Helicopter Society 60th Annual Forum. Baltimore, USA:the American Helicopter Society International, 2004. |
| [5] |
MCKILLIP R M, WACHSPRESS D A, KELLER J D, et al. Distributed multi-vehicle simulation including high-order airwake representation[C]//Proceedings of the American Helicopter Society 60th Annual Forum. Baltimore, USA:the American Helicopter Society International, 2004. |
| [6] |
李鹏, 招启军, 汪正中, 等.
过渡状态倾转旋翼气动力模拟的高效CFD方法[J]. 南京航空航天大学学报, 2015, 47(2): 189–197.
LI Peng, ZHAO Qijun, WANG Zhengzhong, et al. Highly-efficient CFD method for predicting aerodynamic force of tiltrotor in conversion mode[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(2): 189–197. |
| [7] |
李春华, 徐国华.
悬停和前飞状态倾转旋翼机的旋翼自由尾迹计算方法[J]. 空气动力学学报, 2015, 23(2): 152–156.
LI Chunhua, XU Guohua. The rotor free-wake analytical method for tiltrotor aircraft in hover and forward flight[J]. Acta Aerodynamica Sinica, 2015, 23(2): 152–156. |
| [8] |
覃燕华, 朱清华, 邵松.
共轴双旋翼悬停地面效应气动特性分析[J]. 南京航空航天大学学报, 2015, 47(2): 266–274.
QIN Yanhua, ZHU Qinghua, SHAO Song. Aerodynamic characteristics analysis for hovering coaxial rotors in ground effect[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(2): 266–274. |
| [9] |
马艺敏, 陈铭, 王强, 等.
应用PIV测量缩比共轴双旋翼流场特性的研究[J]. 南京航空航天大学学报, 2015, 47(2): 220–227.
MA Yimin, CHEN Ming, WANG Qiang, et al. PIV measurements of model-scale coaxial rotors flow features[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(2): 220–227. |
| [10] |
吴林波, 陈平剑, 李春华, 等.
基于动量源方法的纵列式直升机双旋翼/机身干扰流场分析[J]. 直升机技术, 2009, 159(3): 15–20.
WU Linbo, CHEN Pingjian, LI Chunhua, et al. Analysis on twin-rotor/fuselage interactive flowfield for tandem helicopter based upon momentum-source[J]. Helicopter Technique, 2009, 159(3): 15–20. |
| [11] |
黄水林, 徐国华, 招启军.
纵列式直升机双旋翼流场特性的自由尾迹分析[J]. 空气动力学学报, 2008, 26(4): 473–479.
HUANG Shuilin, XU Guohua, ZHAO Qijun. Free wake analysis on flow field of twin rotors for tandem helicopter[J]. Acta Aerodynamica Sinica, 2008, 26(4): 473–479. |
| [12] |
黄水林, 林永峰, 黄建萍, 等.
基于PIV技术的纵列式双旋翼尾迹特性实验研究[J]. 空气动力学学报, 2012, 30(3): 334–339.
HUANG Shuilin, LIN Yongfeng, HUANG Jianping, et al. Experimental investigation on the wake characteristics of tandem twin rotors[J]. Acta Aerodynamica Sinica, 2012, 30(3): 334–339. |
| [13] |
KUMAR M, MURTHY V R. Analysis of flow around multibladed rotor using CFD in the frequency domain[R]. AIAA 2007-3806, 2007. |
| [14] |
STRAWN R C, AHMAD J, DUQUE E P N. Rotorcraft aeroacoustics computations with overset-grid CFD methods[C]//Proceedings of the American Helicopter Society 54th Annual Forum. Washington DC, USA:the American Helicopter Society International, 1998. |
| [15] |
王阳, 徐国华, 招启军.
基于非结构网格CFD技术的旋翼气动噪声计算方法研究[J]. 空气动力学学报, 2011, 29(5): 559–566.
WANG Yang, XU Guohua, ZHAO Qijun. Numerical method for predicting rotor aerodynamic noise based on unstructured-grid CFD technology[J]. Acta Aerodynamica Sinica, 2011, 29(5): 559–566. |
 2018, Vol. 50
2018, Vol. 50


